Esercizi sullo scambio termico per conduzione e per convezione.
Esercizio 1.
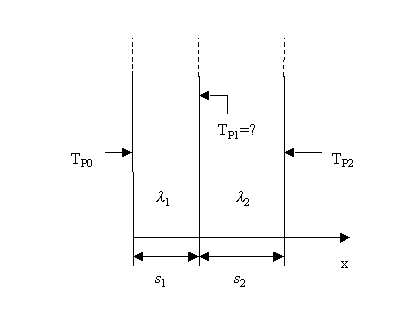
La lastra piana di fig.1 è composta da due strati di materiale diverso e con diverso spessore e conducibilità termica.
Il primo strato ha uno spessore s1, conducibilità termica l 1 e temperatura di parete TP0. Il secondo strato ha invece spessore s2, conducibilità termica l 2 e temperatura di parete TP2.
Calcolare la temperatura TP1 della superficie di contatto tra i due strati e la quantità di calore per unità di superficie che si trasferisce dal primo al secondo strato.

Figura 1 - lastra piana doppia
I dati del problema sono:
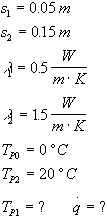
Soluzione:
Per risolvere l’esercizio applichiamo l’equazione di Fourier che per il primo materiale sarà
(1)
Mentre nel caso del secondo materiale
(2)
q. a regime però, è sempre lo stesso poiché il calore uscente è proporzionale a quello entrante, infatti se si verificassero dei fenomeni di accumulo di calore all’interno della lastra inevitabilmente questo porterebbe a delle variazioni di temperatura nel tempo che noi escludiamo quando ci poniamo in regime stazionario.
Essendo l 1 e l 2 costanti e sapendo che i due q. appena calcolati sono uguali possiamo eguagliare le espressioni.
Otteniamo così l’equazione:
(3)
Conosciamo tutte le grandezze tranne TP1 che può essere semplicemente ricavato:
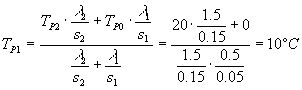
(4)
Questa temperatura è una sorta di media pesata tra le temperature delle pareti estreme i cui fattori di peso sono dati da l/s, che possono essere visti come i reciproci delle resistenze termiche.
Per rispondere al secondo quesito è sufficiente sostituire i valori numerici in qualsiasi delle due equazioni di Fourier ricavate in precedenza, infatti, operando le sostituzioni le due relazioni dovrebbero fornire lo stesso risultato.
Otteniamo così:
materiale 1
![]()
materiale 2
![]()
Di solito è buona regola esprimere il risultato anche in termini di resistenza termica che è definita come D T/Q. . In questo caso avendo calcolato q. e non Q. otterremo come risultato una resistenza termica per unità di superficie. La parete, essendo composta da due superfici, può essere vista come un circuito composto da due resistenze termiche in serie.
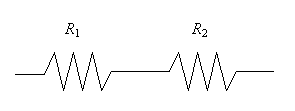
Il valore delle resistenze termiche lo ricaviamo dalla relazione
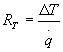
(5)
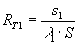
(6)
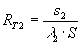
(7)
Come per i circuiti elettrici, le due resistenze in serie equivalgono ad un’unica resistenza totale data dalla somma delle due, RTOT=R1+R2, la resistenza equivalente risulta perciò essere:
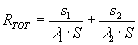
(8)
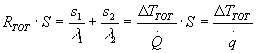
(9)
possiamo così esprimere q. in funzione della resistenza termica
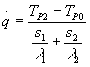
(10)
Da questa formula vediamo che per studiare gli scambi termici di una parete formata da tanti strati di materiali diversi dobbiamo sommare gli s/l , cioè se vi fosse una parete formata da N strati la formula diventerebbe:
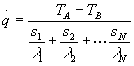
(11)
dove TA e TB sono le temperature di parete del primo e dell’ultimo strato. Quest’ultima formula ci insegna inoltre che spesso possiamo applicare la teoria dell’analogia anche alle resistenze termiche equivalenti.
NOTA: In questo esercizio venivano forniti come dati le temperature di parete, in realtà però, assegnare le temperature di parete significa non fornire condizioni realistiche al contorno del materiale.
Infatti normalmente dobbiamo analizzare problemi in cui vi è una parete solida che separa due ambienti e le temperature misurate non sono quelle delle superfici esterne della parete, ma bensì sono le temperature dell’aria ad una certa distanza dalla parete. Abbiamo quindi la seguente situazione: due ambienti uno a temperatura TA e l’altro a temperatura TB (con ad es. TA>TB), divisi da una parete solida ed in cui le temperature degli ambienti sono state misurate ad una certa distanza dalla parete.
Se ora decidessimo di tracciare un diagramma dell’andamento della temperatura in prossimità della parete, scopriremmo che la temperatura TA rimane costante per vasta regione dello spazio finché non ci si porta a breve distanza dalla parete.
Qui abbiamo una brusca caduta di temperatura, fino a giungere alla temperatura di parete TPA.
All’interno del materiale si verifica una variazione lineare di temperatura che assume il valore TPB (temperatura di parete relativa al secondo ambiente).
Nel secondo ambiente (quello a temperatura minore) l’andamento della temperatura è simile al caso precedentemente descritto, anche qui infatti, si verifica una forte variazione di temperatura in una breve distanza dalla parete solida, quindi un livello di temperatura costante e pari a TB.
Questo strato di fluido in cui avviene il 99% della differenza di temperatura tra parete ed ambiente viene definito come strato limite termico. All’interno di questo strato avvengono i fenomeni di scambio termico convettivo tra aria e parete.
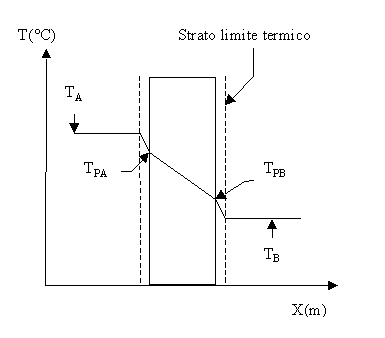
Figura 2 – andamento della temperatura in prossimità della parete
Per quantificare l’effetto dello strato limite termico e quindi l’aumento di temperatura che si crea tra il fluido e la parete bagnata dallo stesso, si definisce una grandezza chiamata coefficiente di convezione, che viene indicato tramite la lettera h ed è definito dalla relazione
(12)
Di solito però, per sapere i valori del coefficiente di convezione non si applica alcuna formula, ma si consulta la normativa che raccoglie i valori dei coefficienti di convezione come stabilito dalla legge.
Abbiamo quindi visto che in un problema di scambio termico che coinvolge una parete vengono assegnate le proprietà della parete in termini di spessore e conducibilità termica, i valori di h nei due ambienti ed i relativi valori di temperatura negli ambienti stessi. Non vengono assegnate le temperature di parete poiché dipendono dalla parete stessa.
Se all’esempio appena citato applichiamo il metodo delle resistenze termiche la situazione da analizzare diventa la seguente:
vi sono 3 resistenze
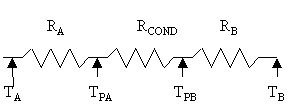
dove RA è la resistenza di convezione che porta la temperatura da TA a quella di parete TPA, RCOND è la resistenza di conduzione del materiale e RB è la resistenza di convezione che fa variare la temperatura dal valore di parete TPB a quella dell’ambiente esterno TB.
Le temperature in questo caso equivalgono alle tensioni presenti in un circuito elettrico.
Per calcolare le resistenze dobbiamo studiarle sull’unità di superficie e otteniamo:
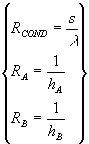
(13)
essendo 3 resistenze in serie la resistenza totale sarà data dalla loro somma
(14)
perciò q. risulta
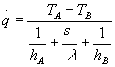
(15)
Questo metodo di calcolo comprende anche i fenomeni convettivi racchiusi nei coefficienti di convezione.
Spesso nei coefficienti di convezione viene incluso anche l’effetto radiante e perciò vengono chiamati coefficienti di adduzione, indicati con il simbolo hTOT.
Esercizio 2
Sia data una parete di mattoni di spessore s, con conducibilità termica l , che divide due ambienti dei quali uno è l’interno di un edificio ed ha temperatura TA e l’altro è l’ambiente esterno all’edificio ed ha temperatura TB.
Determinare lo scambio termico.
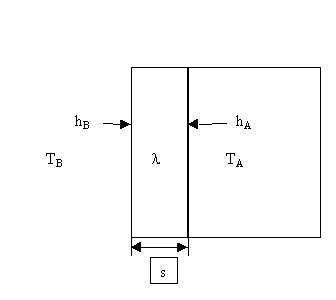
Figura 3 – Parete esterna di un edificio
I dati del problema sono :
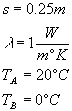
Soluzione:
Per risolvere il problema dobbiamo conoscere i valori dei coefficienti di convezione, che però non sono specificati nel testo.
Utilizziamo perciò la normativa che stabilisce i valori dei coefficienti di convezione in base al luogo da analizzare.
In pianura il coefficiente di convezione per gli interni è
![]()
mentre all’aperto vale
![]()
Ora che conosciamo tutti i dati applichiamo la relazione di calcolo
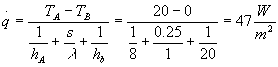
(16)
Per calcolare la potenza che si disperde attraverso la parete, supponiamo che quest’ultima non contenga porte o finestre.
Supponiamo inoltre che la parete abbia una superficie S=50m2.
(17)
Questo risultato indica che all’interno della stanza dovremmo mettere un riscaldatore elettrico da 2350W per mantenere una temperatura di 20 °C, quando all’esterno la temperatura è pari a 0 °C.
NOTA: se invece di considerare la parete come composta da soli mattoni avessimo studiato una parete contenente delle finestre, allora avremmo dovuto analizzare separatamente la superficie di mattoni e quella in vetro.
Esercizio 3
Consideriamo una parete (fig. 3) formata da una lamiera di acciaio di spessore sA a contatto con uno strato di spessore sB formato da blocchi di argilla espansa alternati a blocchi di cemento.
La superficie dei blocchi di cemento è S1, mentre quella dei blocchi di argilla espansa è S2.
Conosciamo inoltre i coefficienti di conducibilità termica dell’acciaio l A, del cemento l B1 e dell’argilla espansa l B2.
Il coefficiente di convezione dell’ambiente a contatto con la lastra di acciaio è hA, quello dell’altro ambiente è hB. Nei due ambienti sono state inoltre misurate le temperature TA e TB.
Calcolare la quantità di calore complessiva Q. scambiato attraverso la parete.
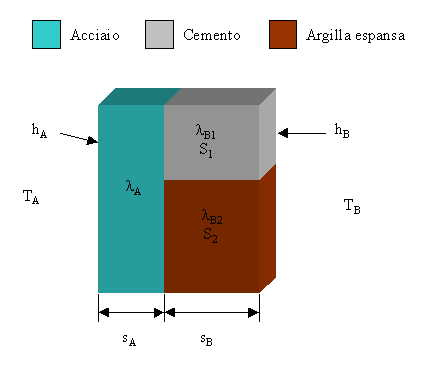
Figura 3 – Parete formata da acciaio cemento e argilla espansa
I dati del problema sono:
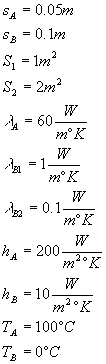
NOTA: in questo caso la lamiera di acciaio è in realtà la parete di una pentola contenente acqua calda a 100 °C, ciò si deduce osservando il valore di hA che sarebbe troppo elevato per l’aria, mentre risulta essere giusto per l’acqua.
Soluzione:
Per risolvere il problema dobbiamo creare la rete elettrica delle resistenze equivalenti. In questo caso abbiamo due possibili cammini uno attraverso i blocchi di cemento e l’altro attraverso i blocchi di argilla espansa, quindi la rete si dovrà biforcare.
Per la risoluzione possiamo costruire più di una rete elettrica, ognuna delle quali fornisce un risultato diverso, nessuna di queste è però migliore delle altre, tutte sono errate. Ciò è dovuto al fatto che la costruzione di queste reti prevede la scomposizione del problema in sottoproblemi ciascuno trattato con la logica della lastra piana indefinita, cioè come se il calore si muovesse solo lungo la direzione x.
A questo esercizio le considerazioni appena esposte non sono applicabili, poiché il calore si muove anche lungo altre direzioni, in particolare la lamiera, che ha conducibilità molto elevata, tende a far scorrere il calore parallelamente alla parete per farlo defluire dove si ha la massima facilità di trasferimento dell’energia, cioè attraverso il cemento, mentre dove abbiamo l’argilla espansa il calore tende a spostarsi cercando altre vie di fuga. La presenza di questi fenomeni di scambio termico paralleli alla superficie non è contemplata dalle nostre equazioni, quindi in qualsiasi modo suddividiamo il problema avremo sempre un errore in difetto, cioè la quantità di calore scambiato sarà sempre superiore a quella calcolata.
Questo effetto viene chiamato ponte termico, cioè in presenza di strutture non omogenee con discontinuità in senso trasversale, il calore tende a ridistribuirsi andando a defluire attraverso le zone più deboli dal punto di vista dell’isolamento termico.
Essendo qualsiasi soluzione errata, scegliamo allora quella più semplice dividendo il flusso sul ramo superiore e su quello inferiore.
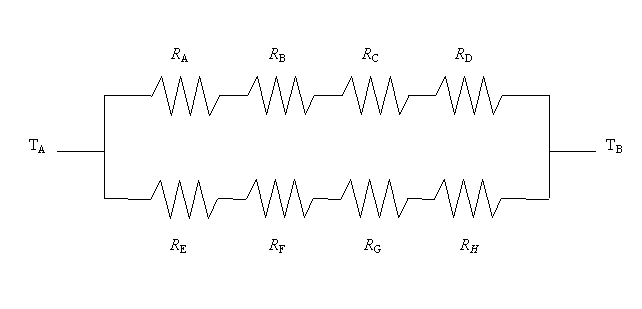
Per calcolare i valori delle resistenze applichiamo la definizione
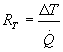
Dobbiamo però considerare che il secondo strato della parete è costituito da due superfici diverse, perciò non possiamo lavorare sull’unità di superficie, ma dobbiamo studiare le aree complessive, in questo caso quindi anche il primo strato verrà trattato come se fosse diviso in due superfici di dimensioni S1 e S2.
Otteniamo così
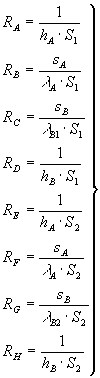
(18)
Essendo i due rami composti da serie di quattro resistenze, possiamo semplificare il circuito con la regola delle resistenze elettriche in serie
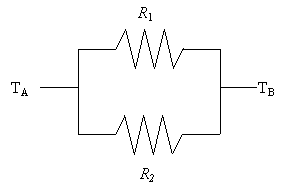
Avremo quindi R1=RA+ RB+ RC+ RD e R2= RE+ RF+ RG+ RH.
Le resistenze R1 e R2 sono in parallelo, quindi per ottenere un’unica resistenza totale utilizzeremo la formula
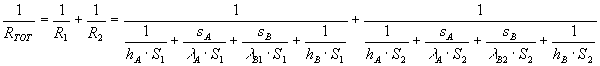
(19)
Utilizzando la relazione
![]()
risulta
(20)
sostituendo i valori numerici risulta
![]()
Poteva essere utilizzato un altro metodo, calcolando la potenza Q1 che fluisce sul primo ramo e la potenza Q2 che fluisce sul secondo.
La loro somma fornisce la potenza totale
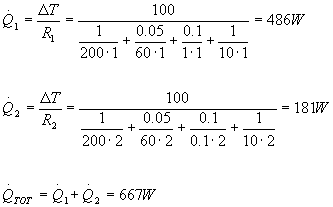
(21)
(22)
(23)
Osservando il risultato e considerando le osservazioni esposte in fase di risoluzione riguardanti le formule applicate, possiamo affermare che per mantenere la temperatura dell’acqua a 100°C, non sarebbe sufficiente l’utilizzo di un riscaldatore da 700W, dovremmo utilizzarne uno da almeno 1200W.
NOTA: nelle nostre equazioni, oltre ai fenomeni descritti precedentemente, dobbiamo trascurare anche il passaggio di calore tra i blocchi di cemento e quelli di argilla espansa, poiché le relazioni che abbiamo utilizzato considerano solo gli scambi termici unidimensionali, per valutare anche la componente di scambio termico tra i due materiali dovremmo risolvere le equazioni di Fourier in due dimensioni il cui calcolo risulta però troppo complesso.
Strumenti di misura della conducibilità termica
Dobbiamo studiare i metodi utilizzati in laboratorio per misurare la conducibilità termica di un materiale.
Vi sono due strumenti principali:
1) La struttura di questo strumento è costituita da due bagni termostatici e da un riscaldatore elettrico.
Il riscaldatore elettrico è formato da una lastra di materiale (di solito di forma quadrata di dimensioni 350x350 mm e di spessore 50 mm), contenente all’interno una resistenza elettrica.
La piastrina riscaldante viene poi contornata da una cornice detta anello di guardia (che porta le dimensioni complessive a 500x500 mm).
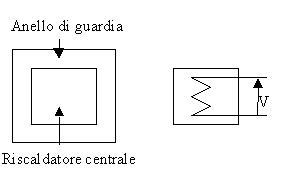
Figura 4 – riscaldatore e anello di guardia visti dall’alto
Il riscaldatore viene posto tra due strati del materiale di cui vogliamo misurare la conducibilità termica. Al di sopra ed al di sotto di questa struttura vengono poste due vaschette contenti del liquido (i bagni termostatici) che servono ad imporre al materiale in prova una temperatura di parete T0 costante. Lo strumento è poi dotato di misuratori di temperatura costituiti da termocoppie collocate sulle due superfici dello strato di materiale da analizzare. Cioè viene misurata la temperatura TC dell’elemento riscaldante e la temperatura T0 del bagno termostatico, conoscendo la potenza Q dell’elemento riscaldante possiamo applicare la relazione
![]()
dove s è lo spessore della striscia di materiale in prova e SR è la superficie dell’elemento riscaldante.
La potenza viene moltiplicata per 2 poiché lo scambio termico avviene su entrambi i campioni di materiale. Conoscendo tutti i dati posso ricavare l .
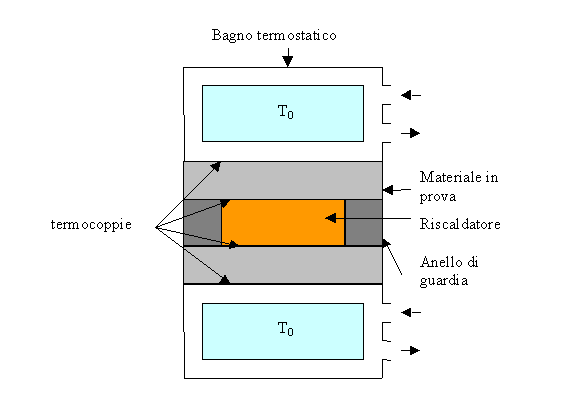
Figura 5 – Piastra termica doppia vista lateralmente
L’anello di guardia serve a realizzare, almeno nella zona centrale, le condizioni ideali di scambio termico monodimensionale.
Questo effetto viene realizzato nel seguente modo:
l’anello di guardia è dotato di un secondo riscaldatore che eroga una potenza QG, tale potenza viene regolata in modo da rendere nullo il gradiente di temperatura tra punti di controllo posti sull’anello di guardia e i corrispondenti punti posti sul riscaldatore centrale, quando il gradiente in direzione y è nullo, tramite la legge di Fourier sappiamo che è nullo anche lo scambio termico.
Cioè la potenza dell’anello di guardia viene regolata in modo da evitare afflussi di calore in senso orizzontale nella lastra centrale.
2)Nel termoflussimetro vi è un solo campione di materiale in prova posto tra due bagni termostatici che hanno temperatura diversa.
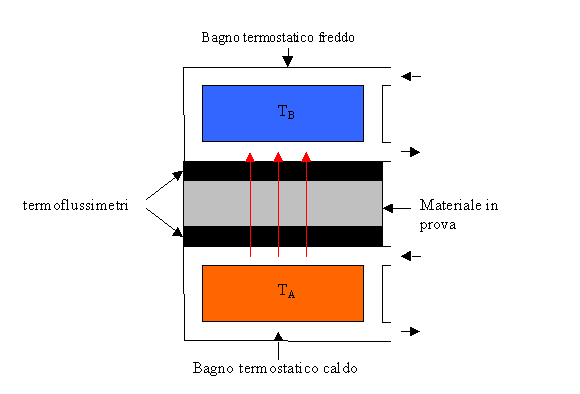
Figura 6 – Termoflussimetro visto lateralmente
Viene fatto circolare un fluido freddo in un bagno ed uno caldo nell’altro in modo che il calore si diffonda dal basso verso l’alto, ovviamente conosciamo le temperature TA e TB dei due bagni. Il problema è determinare la quantità di calore scambiato, poiché non avendo riscaldatori elettrici non possiamo conoscere precisamente la potenza erogata.
Tra lo strato di materiale in prova ed i bagni vengono poste due lastre di gomma di conducibilità nota dette termoflussimetri.
Entrambe le lastre sono dotate di una termocoppia differenziale che è costituita da fili di due materiali (di solito rame e costantana) come mostrato in figura 7.
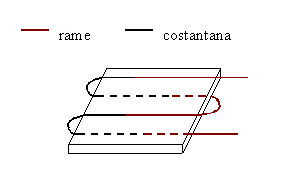
Figura 7 - termoflussimetro
Questo filo costituito da continue giunzioni rame/costantana, è avvolto attorno al termoflussimetro in modo da avere tante giunzioni distribuite sulla superficie dello stesso su entrambe le facce, ma con sempre le giunzioni rame/costantana sulla faccia superiore e costantana/rame su quella inferiore.
Finito l’avvolgimento esce un filo di rame che viene collegato ad un voltmetro, la tensione misurata non è proporzionale alla temperatura del termoflussimetro ma è direttamente proporzionale alla differenza di temperatura delle due lastre.
Quindi il segnale elettrico è proporzionale al flusso termico a meno di una costante di temperatura data da s/l .
Il segnale elettrico viene mandato ad uno strumento che grazie ad un fattore di scala opportuno legge direttamente il flusso in W/m2.
Sapendo che la densità di flusso è
![]()
possiamo ricavare l .
La termocoppia differenziale è molto utile soprattutto perché consente di avere un segnale elettrico molto forte anche per differenze di temperature ridotte.