Alessandro Gregori – matr. 117852 – Lezione del 24/1/2000 – ora 10:30-12:30

Le superfici alettate rappresentano un metodo molto utilizzato per consentire il raffreddamento di superfici che risentono degli effetti del surriscaldamento (ad esempio i transistor di potenza). La loro funzione è agevolare lo scambio termico tra la superficie e il fluido circostante (normalmente aria in convezione naturale) tramite l’aumento della superficie di scambio stessa. Si sa che l’aria è un pessimo scambiatore e in convezione naturale lo scambio è ancora minore; quindi in assenza di ventole che stabiliscano una convezione forzata sulla superficie in questione, la tecnica migliore è quella di ricoprirla di alette (si tratta di una soluzione ampiamente sfruttata nell’elettronica di consumo).

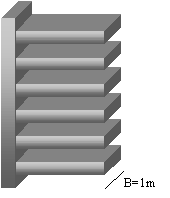
Figura 1: alettatura

Per comodità si considereranno alette che si stendono su una superficie di lunghezza B=1m.

Le alette possono essere sagomate in diversi modi (alcuni esempi sono in Figura 2). Le alette triangolari o di forma simile sono migliori di quelle rettangolari, ma molto più complesse da calcolare; per i calcoli, quindi, saranno prese in considerazione solo alette rettangolari.

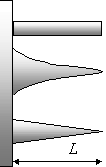
Figura 2: possibili profili di alette

È da notare che la lunghezza L dell’aletta è un fattore non secondario: infatti alette troppo lunghe sarebbero controproducenti, facendo da freno alla circolazione dell’aria nelle altre alette, mentre se fossero troppo corte lo scambio termico sarebbe ridotto. Esiste quindi una dimensione ottima. In ogni modo, nei calcoli che seguono l’effetto frenante delle alette viene trascurato e si considera lo scambio termico per pura convezione con l’esterno.

La figura 3 mostra come la temperatura dell’aletta decresca man mano che ci si allontana dalla base (T_P = temperatura di parete, T_¥ = temperatura ambiente).

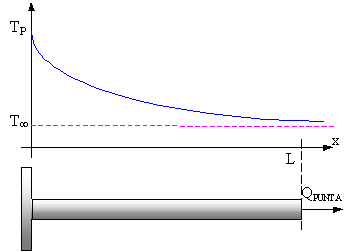
Figura 3

Si fa un’ulteriore ipotesi semplificativa: si trascura la quantità di calore scambiato dalla superficie di testa dell’aletta (Q_PUNTA=0). Si vedrà più avanti che non è un’ipotesi sempre accettabile.

Normalmente le alette non vengono fuse insieme alla superficie che devono raffreddare (soprattutto nel caso di microprocessori, transistor…); vengono invece "riportate". Questo fa sì che si presenti una resistenza di contatto R_C nell’interfaccia superficie/aletta che causa una piccola caduta alla base dell’aletta stessa (che quindi viene a trovarsi ad una temperatura inferiore a T_P).

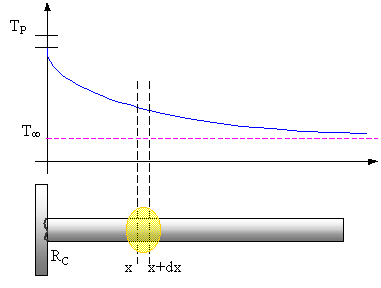
Figura 4

L’area evidenziata in figura 4 (il "concio" elementare di lunghezza dx) viene rappresentata in dettaglio in figura 5. Si noti che la densità di flusso è massima alla base dell’aletta, in quanto la differenza di temperatura tra metallo e aria è più marcata. Le quantità di calore scambiate (indicate come flussi di calore) sono infinitesime lungo i fianchi dell’aletta in quanto si prende in considerazione un tratto infinitesimo della stessa.

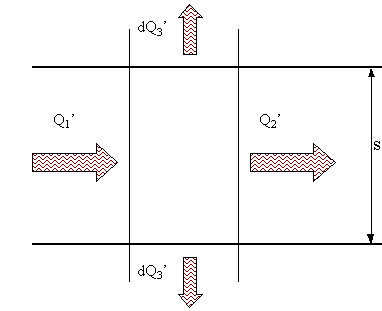
Figura 5: tratto di aletta di lunghezza dx

All’equilibrio quindi il bilancio dei flussi di calore scambiato sarà

(1)

Sapendo che l è la conducibilità termica del materiale dell’aletta possiamo esprimere la legge di Fourier per esprimere la relazione tra densità di flusso di calore e gradiente di temperatura

(2)

(3)

Conoscendo la relazione tra calore e temperatura per la convezione, dalla (1) possiamo scrivere

(4)

(in cui h è il coefficiente di convezione) e dalle equazioni (2) e (3)

(5)

Da (4) e (5) si può ottenere

(6)

in cui, chiamando q = T(x)-T(¥) è possibile riconoscere un’equazione differenziale a variabili separabili di 2° grado.

(7)

Posto

(8)

la (7) ha l’aspetto dell’equazione di Helmoltz (in cui, però, compariva il termine –m²). Riutilizzando il risultato ottenuto in acustica, la soluzione è

(9)

che è una soluzione smorzata (non oscillante come nel caso dell’equazione di Helmoltz).

Al fine di trovare le costanti A e B è necessario imporre delle condizioni al contorno a x=0 e a x=L. La presenza della R_C rende il calcolo più complesso.

Per x=0

(10)

Mentre per x=L

(11)

Possiamo quindi ottenere i valori delle due costanti A e B

che sostituiti nelle (9) permettono di trovare l’espressione

(12)

L’equazione (12) rappresenta un risultato che, nella pratica, non viene utilizzato. Infatti risulta molto più utile definire il confronto tra lo scambio termico in presenza dell’aletta e quello in assenza della stessa.

In una striscia di larghezza s il flusso di calore scambiato dalla parete sarà

(13)

mentre il flusso di calore in presenza dell’aletta è

(14)

Facendo il rapporto tra la (14) e la (13) si definisce il guadagno dell’aletta.

(15)

Il guadagno è un numero ³ 1 ed è la relazione effettivamente usata nella pratica in quanto dà l’incremento di scambio termico determinato dalla presenza dell’aletta. Si noti che G ha un tetto massimo. Infatti se tutta l’aletta fosse alla temperatura costante T_P il flusso di calore sarebbe

(16)

il che porta alla definizione di un secondo parametro caratteristico dell’aletta, l’efficienza.

(17)

Dalla (15) e dalla (17) si può ottenere

(18)

Si tratta di un risultato molto interessante, in quanto mostra che, a parità di efficienza, il guadagno aumenta mettendo alette lunghe e sottili.

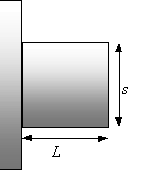
Figura 6: aletta tozza

Il caso dell’aletta tozza è un caso limite: ponendo L=s e considerando l’efficienza unitaria (efficienza massima) infatti si può ottenere il guadagno dalla (17): G = 2. È evidente però dalla figura che la quantità di calore dispersa dal "dado" è 3 volte maggiore di quella dispersa dalla superficie in sua assenza. Questo errore dipende dall’aver trascurato il calore scambiato dalla superficie di testa dall’aletta (ipotesi semplificativa iniziale). Per inserirla nelle equazioni ricavate finora si ricorre ad un piccolo artificio: si immagina di spostare una metà della superficie di testa su un lato dell’aletta e l’altra metà sull’altro lato (vedi figura 7).

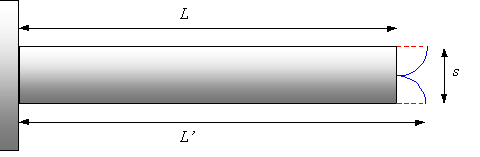
Figura 7: lunghezza efficace dell'aletta

Nelle equazioni ricavate precedentemente basta quindi sostituire L con

(19)

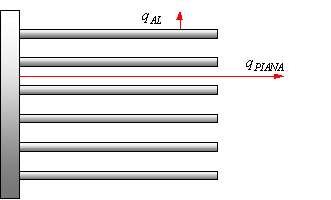
Figura 8

Avendo studiato lo scambio termico di una singola aletta, possiamo prendere ora in considerazione una superficie alettata. Indichiamo con

• S_TOT la superficie di partenza che vogliamo raffreddare,
• S_AL la porzione su cui vengono montate le alette,
• q_PIANA la densità di flusso della superficie piana,
• q_AL quella delle alette,
• e _A l’efficienza della singola aletta.

Vogliamo ricavare l’efficienza e _TOT dell’intera superficie alettata.

La potenza termica totale sarà data dalla somma dei contributi delle alette e della superficie piana

(20)

La densità di flusso della superficie piana è

(21)

Dalla definizione di G possiamo anche scrivere

(22)

Sostituendo nella (22) le espressioni di G e di q_PIANA

(23)

Ora conosciamo tutti i termini per esprimere il flusso totale

(24)

Conoscendo

(25)

possiamo esprimere il guadagno totale del sistema

(26)

e soprattutto l’efficienza totale dell’alettatura

(27)

Nel caso di alette non rettangolari il diagramma dell’efficienza viene fornito dal costruttore e le alette possono essere distinte dal fattore di forma. Vengono riportati due grafici a titolo di esempio. Si noti come le alette triangolari siano più efficienti di quelle rettangolari.

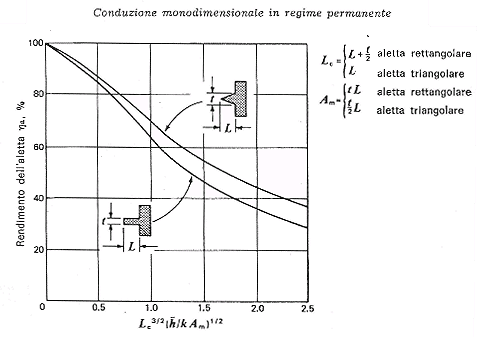
Figura 9: rendimento di alette rettangolari e triangolari

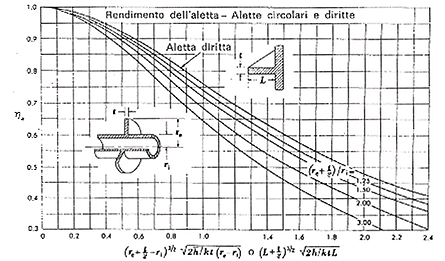
Figura 10: rendimento di alette circonferenziali a sezione trasversale rettangolare

La CPU di un computer è dotata di una superficie piana addetta al raffreddamento della stessa. Si vuole conoscere la temperatura che raggiunge detta superficie sapendo che:

• è quadrata e di lato L = 50mm;
• deve dissipare una potenza di 20W;
• la temperatura ambiente è T¥ =20°C e la temperatura di parete è T_P=100°C.

Nel caso la temperatura trovata sia eccessiva, si determini una superficie alettata di raffreddamento adeguata.

Figura 11: superficie di raffreddamento di una CPU

Per risolvere l’esercizio abbiamo bisogno dei numeri di Grashof, Prandtl e Nusselt e per trovare la formula adatta, anche del numero di Rayleigh. È noto che per l’aria in condizione naturale il numero di Prandtl è

Per trovare il numero di Grashof

dobbiamo conoscere:

• accelerazione di gravità g=9,81m/s2;
• coefficiente di dilatazione termica (che nel caso di gas è l'inverso della temperatura) b » 1/333 °K^-1;
• viscosità cinematica m =16.10-6m2/s.

Ora possiamo calcolare Gr:

Conoscendo i numeri di Grashof e Prandtl possiamo calcolare il numero di Rayleigh

che, come si può vedere è 10⁹. Siamo in convezione naturale e la formula che utilizzeremo è quella di McAdams

Possiamo ricavare

Per ottenere h_TOT a questo termine va sommato quello dovuto all’irraggiamento che è

Si ricava così

Dalla (13) possiamo ricavare T_P

La temperatura trovata è evidentemente troppo elevata per un componente elettronico e causerebbe danni alla CPU. Procediamo quindi alla realizzazione di una adeguata alettatura (che potrebbe essere, per esempio, di alluminio).

Scegliamo le seguenti misure per il sistema:

• lunghezza delle alette: L_A = 20 mm;
• sezione trasversale della singola aletta: s = 3 mm;
• distanza tra due alette adiacenti d = 3 mm.

È evidente che, per coprire la superficie in questione, che è un quadrato di 50 mm di lato, sono necessarie 8 alette.

Possiamo quindi calcolare la superficie totale S_TOT e la porzione di essa coperta dalle alette S_AL.

Ricaviamo anche l’efficienza totale

Figura 12: alettatura di raffreddamento di una CPU

Sapendo che la CPU deve dissipare una potenza di 20W, possiamo riscrivere la (24)

cioè

Possiamo quindi ricavare la T_P

Il valore di temperatura trovato è accettabile, quindi l’alettatura presa in esame è da considerare valida per il raffreddamento del dispositivo.