Gianpietro Germi matr.117405 Lezione del 12/10/99 - ora 14:30 - 16:30
Università degli Studi di Parma
Corso di Fisica Tecnica
La lezione si propone di risolvere alcuni problemi, utilizzando principalmente il secondo principio della termodinamica. Facendo particolare riferimento alla sua versione legata alla macchina di Carnot, il cui coefficiente economico è definito come:
![]()
![]()
Rendimento Termodinamico
Definiamo un’altra grandezza, che chiamiamo rendimento termodinamico,
![]()
cioè il rapporto tra il rendimento della macchina termica utilizzata e quella di Carnot, che lavora tra le stesse temperature.
Potere calorifico inferiore Pci e potere calorifico superiore Pcs
Il Pci indica l’Energia prodotta bruciando una certa quantità di combustibile in presenza della quantità stechiometrica minima di vapore acqueo necessario per la combustione.
Il Pcs, invece, si utilizza quando si brucia il combustibile in eccesso di vapore acqueo.
La differenza consiste nel fatto che, ad una certa temperatura, chiamata Temperatura di Rugiada ( o di Condensa ), la presenza di vapore acqueo in eccesso consente una minore riduzione della temperatura dei fumi di combustione quando gli si sottrae calore. Questo calore, infatti, viene fornito in parte dalla condensazione del vapore, che cambiando stato cede Energia.
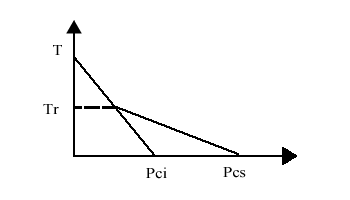
La differenza tra Pci e Pcs dipende dal tipo di combustibile.
Ad esempio, con il carbone, la differenza è minima. Infatti la sua combustione produce poco vapore acqueo. Con il metano, invece, la differenza è notevole (circa il 30 % in più ), poiché questo crea molto vapore acqueo nella combustione.
C + O2 = CO2
CH4 + 2O2 = CO2 + 2H2O
L’utilizzo del vapore acqueo è usato solo nelle caldaie a condensazione, mentre nelle altre viene eliminato, perché la condensa danneggia le apparecchiature.
Esercizi
Il primo problema da affrontare riguarda una locomotiva che percorre una salita a velocità costante. Questa macchina possiede una massa di 100 tonnellate e procede ad una velocità di 80 Km/h. La sua caldaia brucia 1 tonnellata di carbone all’ora alla temperatura di 100º C, con un rendimento termodinamico di 0,25 e un potere calorifico inferiore di 14.000 BTU/lb. Si chiede quanto vale la pendenza della salita (misurata nei termini dell’angolo q ).
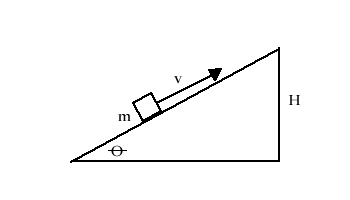
T1 = 100° |
m = 100 tonn T0 = Tamb = 20° |
v = 80 Km/h Pci = 14.000 BTU/lb |
Risoluzione
Come prima cosa bisogna convertire i dati nelle grandezze del S.I.
Una BTU è definita come la quantità di calore necessaria per aumentare di 1° F la temperatura di una libbra di acqua.
Quindi, sapendo che
1 BTU = 1,055 KJ
1 lb = 0,4536 Kg
Calcoliamo
1 BTU/lb = 2,33 KJ/Kg
Possiamo adesso calcolare la potenza sviluppata dalla caldaia:
![]()
Possiamo rappresentare il sistema come una macchina termica che lavora tra la caldaia e l’ambiente. Se consideriamo una macchina di Carnot, il suo coefficiente economico vale :
![]()
Quindi, conoscendo il rendimento termodinamico della nostra macchina, possiamo calcolare il rendimento reale:
![]()
La potenza utile al moto della locomotiva quindi vale:
![]()
Tutto questo vale se consideriamo l’attrito delle rotaie e la resistenza dell’aria già compresi nel rendimento termodinamico ( potremmo anche averli trascurati ).
Dalla meccanica sappiamo che:
![]()
Quindi applichiamo questa legge nell’unità di tempo, infatti Lu è il lavoro svolto per ogni ora, cioè una potenza.
![]()
Quindi l’altezza percorsa in un’ora è
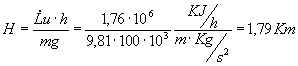
Dopo un’ora la locomotiva ha percorso uno spazio l =80 Km, quindi
![]()
Affrontiamo ora il problema del lavoro massimo ottenibile da un sistema e lavoro minimo applicabile ad un sistema.
Consideriamo il caso di una macchina termica che lavora con il serbatoio freddo vicino allo zero assoluto, mentre quello caldo a temperatura ambiente.
Si cerca il costo minimo per estrarre una quantità di calore di 1 KJ, lavorando con la macchina di Carnot e considerando il prezzo dell’Energia di 150 lit/Kwh.
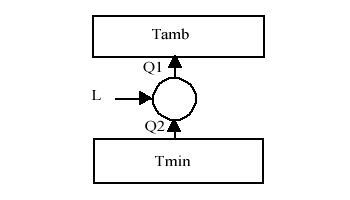
| Tmin = 0,001 K | Tamb = 20° C | Q2 = 1 KJ |
Risoluzione
Calcoliamo il coefficiente economico
![]()
E’ importante non approssimare il dato, perché questo valore verrà confrontato con uno molto vicino, quindi basta un piccolo arrotondamento per creare un grande errore.
Dal primo principio della termodinamica si ha
![]()
Quindi calcoliamo il lavoro minimo per estrarre Q2 dal sistema
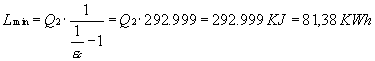
Non resta che calcolare il costo minimo di questa operazione, che è di 12.208 lit.
Questa operazione si rivela molto costosa rispetto alla piccola quantità di calore rappresentata da Q2. Il lavoro necessario sarebbe stato minore se il serbatoio freddo avesse avuto una maggiore temperatura. Infatti il coefficiente economico sarebbe stato minore e quindi, a parità di calore sottratto, minore anche il lavoro.
L’ultimo problema si occupa di lavoro massimo ottenibile dal sistema.
Consideriamo un bidone di volume 1 m3 contenente acqua alla temperatura di 100° C che lavora come serbatoio caldo in una macchina di Carnot che ha il serbatoio freddo a Tamb = 20° C. Si cerca il lavoro massimo ottenibile.
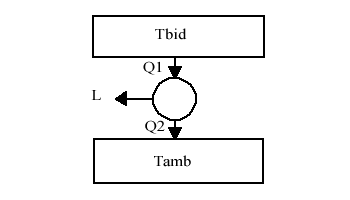
Risoluzione
Un approccio sbagliato al sistema potrebbe portare a considerare questo come una macchina semplice, cioè una macchina che lavora con due serbatoi a temperatura costante, mentre la temperatura del bidone varia.
Questo tipo di soluzione è utile però per avere un idea dell’ordine di grandezza della soluzione esatta, per non imbattersi in calcoli matematici complicati senza avere un riscontro con cui verificare il senso del risultato ottenuto.
Questo approccio porta quindi ad una soluzione
![]()
Dove M è la massa del bidone (densità acqua = 1 Kg/dm3 ) e Cv è il calore specifico a volume costante dell’acqua, cioè 1 cal/g o 4,167 KJ/Kg.
In realtà possiamo considerare la macchina semplice solo per cicli infinitesimi, infatti la temperatura del bidone cala mano a mano che gli si sottrae calore. In particolare la pendenza della retta di decrescita è data dal calore specifico.
Il lavoro massimo si ottiene esaurendo il processo, cioè quando la temperatura del bidone raggiunge quella dell’ambiente e allora la macchina non funziona più.
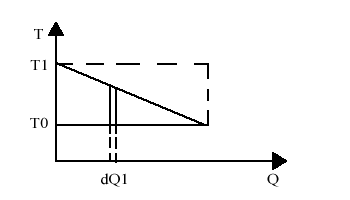
Quindi vale solo
![]()
Dove
![]()
Infatti il bidone non consente variazioni di volume, di conseguenza il lavoro sul bidone è nullo. Quindi dal primo principio dQ = dU , che si esprime proprio con quella formula. In particolare il meno significa che a decrementi di temperatura del bidone corrispondono quantità di calore assorbite dal sistema e quindi dQ positivi. Questo si spiega col fatto che dQbid = -dQsis, perché quando uno cede, l’altro assorbe e il segno si regola con la convenzione.
Calcoliamo il coefficiente economico di questa macchina
![]()
Quindi per ogni ciclo infinitesimo
![]()
Calcoliamo l’integrale per ottenere il lavoro massimo
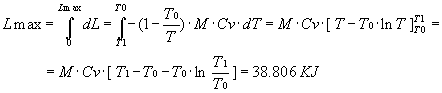
Otterrei una soluzione approssimata a questa osservando la figura precedente.
L’area del ciclo è all’incirca un triangolo, cioè la metà dell’area ottenuta considerando costante la temperatura del bidone. Quindi il risultato di questo metodo ottenuto con una buona approssimazione ( circa 8 % ), è circa 36.000 KJ.
Una soluzione alternativa a queste si ottiene con il principio della non diminuzione dell’entropia dell’Universo.
In questo caso il lavoro massimo si ottiene se non varia l’entropia dell’Universo, cioè con tanti cicli reversibili.
Dopo ogni ciclo
![]()
Dove
![]()
![]()
e D Sm è nullo.
In questo integrale dQ1 ha segno positivo in quanto la variazione di entropia si ha sul bidone e quindi non più del sistema e in base alle considerazioni fatte in precedenza tolgo il meno. Questo accorgimento è giustificato dal fatto che a variazioni negative di dT corrispondono variazioni negative di dQ.
Quindi
![]()
E di conseguenza
![]()