ANALISI IN FREQUENZA
C’è un altro metodo di rappresentazione di un segnale, oltre alla descrizione nel dominio del tempo che abbiamo visto sino ad ora: la descrizione in frequenza; l’obiettivo dell’analisi in frequenza è quello di definire il contenuto energetico di un suono complesso, che contiene cioè componenti a diverse frequenze, che possono variare istante per istante.
Per analizzare un segnale s(t) in frequenza, si parte dalla sua rappresentazione nel dominio del tempo, cioè la sua forma d’onda, per arrivare a definire tramite una conversione lo spettro, vale a dire una descrizione del segnale in un piano cartesiano avente le frequenze in ascisse e il livello in dB in ordinata.
OSS. La forma d’onda è una curva che visualizza l’andamento di un segnale elettrico generato da un microfono, il quale si basa in genere sulla variazione della pressione nel mezzo in cui è "immerso".

Fig.1 Spettro di un segnale
E’ importante precisare che tutte le tecniche di conversione oggi note sono imperfette: a tutt’oggi infatti, non esiste un’apparecchiatura in grado di riprodurre con precisione i fenomeni d’analisi in frequenza che avvengono nel nostro orecchio.
Nell’analisi in frequenza di un segnale si è soliti distinguere in due casi:
Nel primo caso (il più semplice) oggetto di studio sono segnali sempre uguali a se stessi, di cui possiamo quindi analizzare le frequenze una alla volta mettendo insieme i risultati: per questo l’analisi frequenziale è semplice, tanto che i sistemi di conversione eguagliano, e a volte superano, la percezione umana.
OSS. Un motore elettrico, una volta avviato a velocità costante, è un esempio di sorgente di segnale stazionario. Nel secondo caso invece, si prendono in considerazione segnali che variano in maniera non prevedibile nel tempo e quindi l'analisi non riesce ad eguagliare le capacità umane.
Nel secondo caso invece, si prendono in considerazione segnali che variano in maniera non prevedibile nel tempo e quindi l'analisi non riesce ad eguagliare le capacità umane.
Filtro d’ottava
Introduciamo ora le tecniche di conversione per segnali di tipo stazionario. Un metodo, risalente agli anni 60’, consiste nel fare uso del cosi’ detto banco di filtri: si dispone di una serie di più filtri passa-banda (tipicamente 10 filtri d’ottava),ed attraverso un selettore si varia il percorso del segnale elettrico in modo che entri in uno dei filtri; l’uscita di quest’ultimo è collegata ad un misuratore (solitamente un voltmetro a lancetta), che mi restituisce il livello di segnale che compete al particolare intervallo di frequenze (fig. 2).
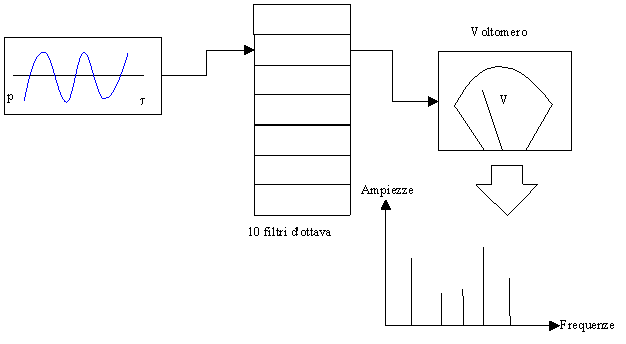
Fig.2 Analizzatore di segnali stazionari
OSS. Un filtro passa banda è un dispositivo che passare solo un determinato campo di frequenze, reiettando le componenti del suono a frequenze maggiori e minori.
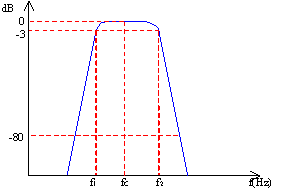
Fig.3 Funzione di trasferimento di un filtro passa banda
In un grafico in funzione della frequenza di un filtro passa banda si individuano due caratteristiche principali:
taglio, poste a metà energia rispetto alla banda passante:
(1) ![]()
In un filtro ideale la pendenza dei fianchi è di 90° mentre in quelli reali è minore; per fare in modo che la misura sia più precisa possibile, la pendenza deve essere compresa in maschere d’accettabilità previste dalle norme emesse dall’IEC (International Eletrotechnical Commission, un’organizzazione che si occupa della definizione degli standard per le misure acustiche): IEC 1260:1995-08 oppure CEI EN 61260.
3. ANALISI DEI SEGNALI TRANSIENTI
Il metodo di conversione per segnali transienti è in parte simile a quello utilizzato nel caso stazionario. Si utilizza anche in questo caso il banco di filtri, con una differenza fondamentale rispetto al caso precedente: Invece di avere un solo voltometro, ne abbiamo uno per ogni filtro attraverso cui passa il segnale, che viene mandato contemporaneamente a tutti i filtri:
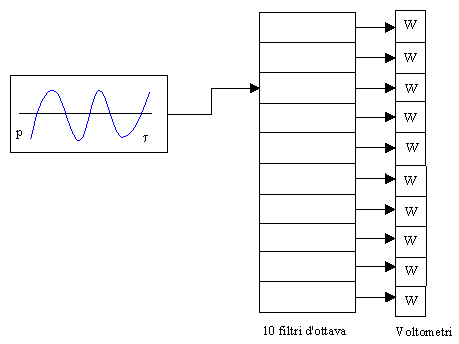
Fig.4 Analizzatore di segnali transienti
Con un oggetto di questo tipo misuriamo l’ampiezza di tutte le frequenze simultaneamente, da questo il nome "analizzatore in tempo reale" o RTA (Real Time Analyzer).
Si è notato che i filtri ad ottave hanno una larghezza di banda abbastanza elevata (il rapporto tra frequenze di taglio inferiore e superiore è di ˝), e al fine di misurazioni più precise si è avvertita l’esigenza di utilizzare filtri a banda più stretta (frazione d’ottava) mantenendo però il concetto di proporzionalità tra ampiezza di banda e frequenza di centro banda.
Ottava e frazioni d’ottava
Si definisce ottava un intervallo di frequenze in cui il limite inferiore f1 e quello superiore f2 verificano la seguente relazione:
(2) ![]()
Al fine di coprire l’intero campo delle frequenze udibili occorrono 10 filtri d’ottava, caratterizzati dal fatto che ciascuno ha frequenza di centro banda doppia rispetto al filtro precedente:
|
Fc1 |
Fc2 |
Fc3 |
Fc4 |
Fc5 |
Fc6 |
Fc7 |
Fc8 |
Fc9 |
Fc10 |
|
31,5Hz
|
63Hz |
125Hz |
250Hz |
500Hz |
1KHz |
2KHz |
4KHz |
8KHz |
16KHz |
Quando la suddivisione dell’asse delle frequenze in bande d’ottava risulta eccessiva (come nel nostro caso) si ricorre all’uso di filtri a banda più stretta (a frazione d’ottava), pensati in maniera tale da mantenere la proporzione tra la larghezza di banda e la frequenza di centro banda:
(3) ![]()
Per i filtri d'ottava questo valore costante è pari a
(4) ![]()
I filtri che hanno questo rapporto costante sono chiamati FILTRI AD AMPIEZZA PERCENTUALE COSTANTE: attraverso questa caratteristica si fa in modo che la frequenza f2 di ogni filtro diventi la frequenza f1 del filtro successivo, in modo da coprire completamente tutto l’intervallo di frequenza interessato. La scelta di questo metodo di suddivisione delle frequenze avviene in special modo perchè il sistema uditivo umano risponde agli stimoli più secondo lo schema dell’apertura percentuale costante che secondo quello dell’apertura costante.
Esistono diversi tipi di filtri, a seconda del numero di parti in cui viene divisa ogni banda:
La scala più usata è quella dei terzi d’ottava, formata da 30 bande da 1/3 d’ottava ciascuna.
Come esempio prendiamo in esame un filtro da 1/3 l’ottava, e vediamo come risulta la suddivisione della banda d’ottava che ha fc=1000 Hz; cerchiamo cioè le frequenze di centro banda fc1, fc2, fc3, e gli estremi di ogni banda f1, f2, f3 e f4.
Sappiamo innanzi tutto che
(5) ![]() Hz
Hz ![]() Hz
Hz
Devono risultare verificate le seguenti condizioni:
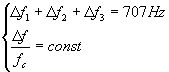
Ora definiamo:
(7) ![]() i = 1,2,3...
i = 1,2,3...
dove K è il rapporto tra due frequenze di centro banda consecutive.
Ora , per la definizione d’ottava è:
Per la definizione d'ottava:
(8) ![]() quindi
quindi ![]() .
.
Considerano che la relazione (7) vale anche per le frequenze di taglio, ricaviamo:
(9) 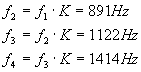
e anche:
(10) 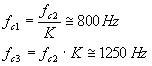
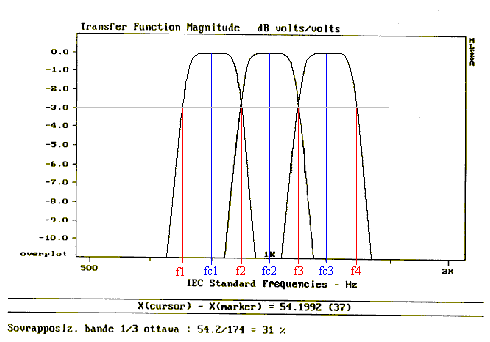
Fig.5
Dal grafico si può osservare che, se la frequenza di un suono puro cade nella zona in cui due bande da 1/3 d’ottava si sovrappongono, lo spettro ha energia in due diversi intervalli di frequenze.
OSS. Risulta curioso osservare come uno spettro di un segnale, a seconda della tecnica utilizzata, possa cambiare il proprio spettro.Osserviamo come esempio gli spettri di figura 5 , uno a frequenza lineare :
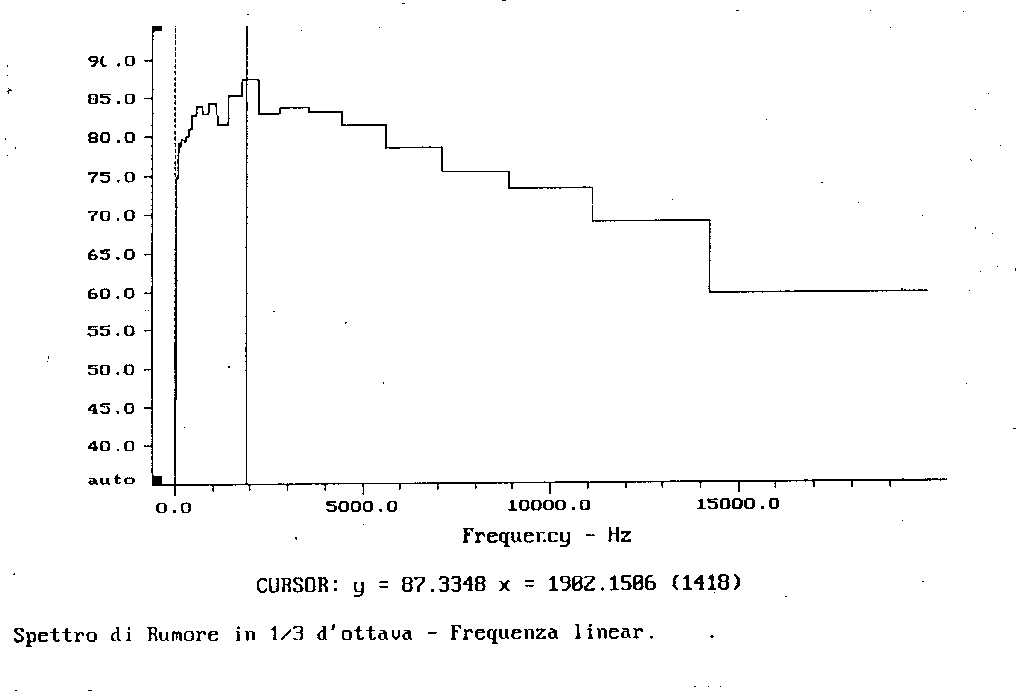
Fig. 6a
L’altro a frequenza logaritmica:
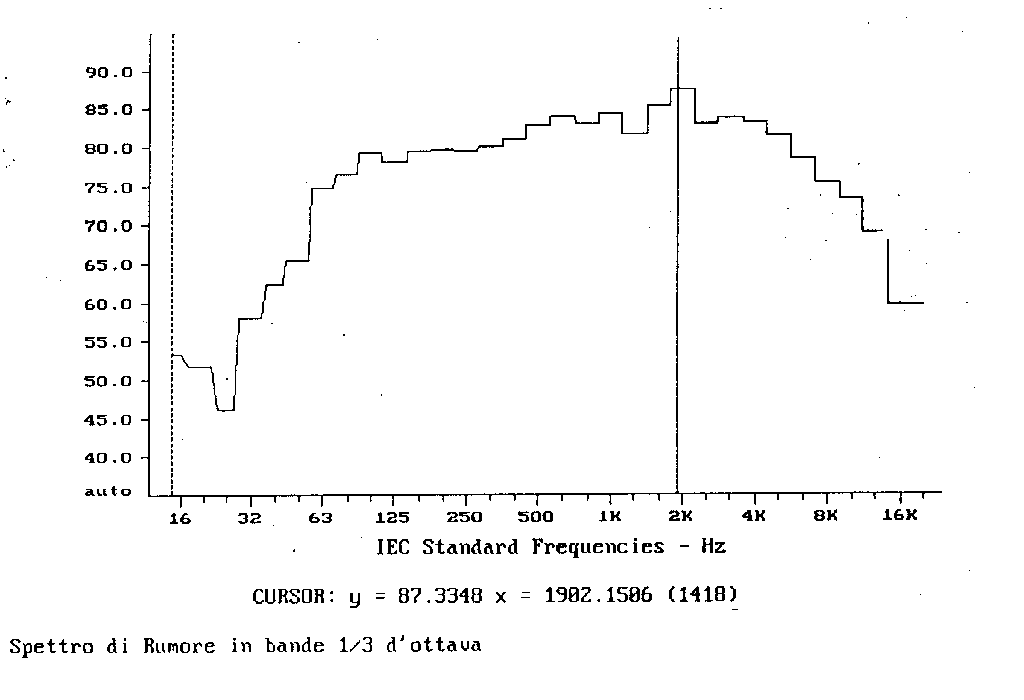
Fig. 6b
Le figure 6.a e 6.b rappresentano due spettri che sono stati ottenuti dallo stesso segnale con cui si sono ricavati quelli sopra, ma con una definizione assai maggiore di quella ottenuta con banda ad 1/3 d’ottava; sono infatti grafici ottenuti al calcolatore che in generale lavora con bande ad apertura costante e stretta (stretta può significare anche 20000 valori nell’intero campo dell’udibile).
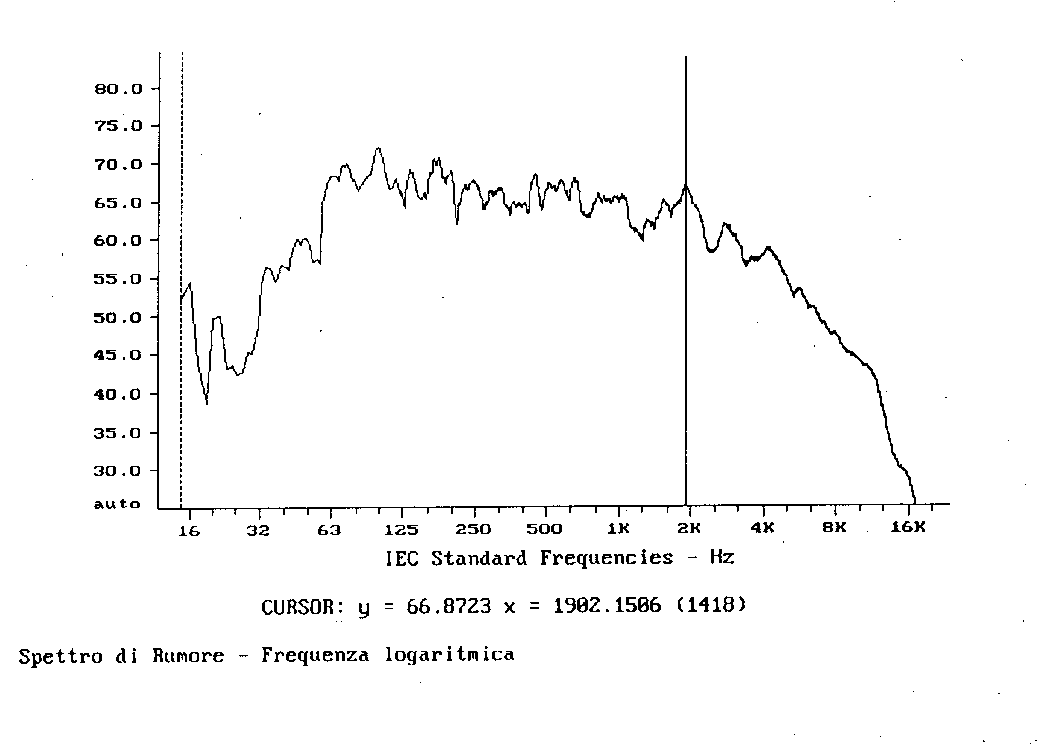
Fig. 7a
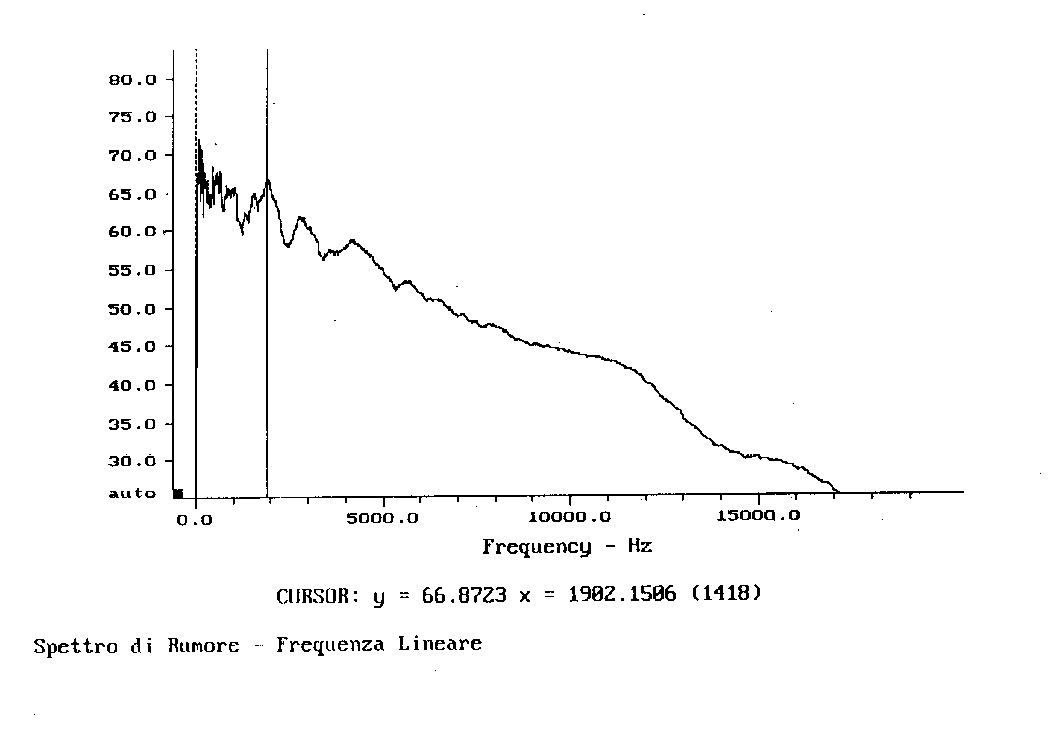
Fig. 7b
E’ importante sottolineare, in questi grafici, la presenza del cursore (la riga verticale sullo spettro) che per tutti e quattro i grafici è posizionato ad una frequenza fissa pari a 1902,15 Hz circa. Esso sottolinea come il livello, nelle bande di 1/3 d’ottava, sia ben più alto di quanto non sia nel caso di bande ad ampiezza costante strette.
Altro metodo per lo studio dello spettro di un segnale è l’analisi in frequenza, altrimenti detta analisi di Fourier; essa si basa matematicamente sulla teoria nota come Discrete Fourier Transport (Trasformata discreta di Fourier), il cui calcolo è oggi affidato completamente ai calcolatori
Nell’analisi in frequenza, oltre all’ipotesi di stazionarietà, occorre anche sia soddisfatta un’ulteriore ipotesi: la periodicità; pertanto non può essere utilizzata per segnali che variano in modo imprevedibile come la voce umana.
La base matematica di questo metodo d’analisi è il TEORMA DI FOURIER:
Un suono complesso, ma periodico, è sempre rappresentabile dalla sovrapposizione di un infinito numero d’onde sinusoidali ciascuna dotata d’opportuna ampiezza e fase.
(11) ![]()
Nella realtà, però, non possiamo calcolare un numero infinito di sinusoidi; le tecniche d’elaborazione matematica al calcolatore rendono facile il calcolo delle ampiezze e delle fasi per rappresentare il suono solo se le frequenze variano con una legge logica; per tanto, si segue la regola secondo cui le frequenze wit devono equidistanti tra loro, e le componenti frequenziali devono essere in numero finito.
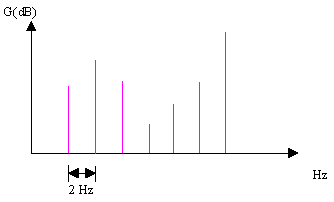
Fig.8
In questo caso non si parla più di analisi di Fourier in senso stretto, ma di analisi discreta in relazione ad una legge matematica inderogabile.
4. CAMPIONAMENTO
Per campionamento di un segnale s’intende la scelta di un intervallo di tempo DT (periodo di campionamento) e il successivo prelevamento dei valori del segnale in istanti multipli di DT.
Il periodo di campionamento utilizzato più frequentemente è DT=22,676 ms, dal quale si ricava una frequenza di campionamento fc = 44100 Hz; pertanto, se campioniamo un segnale il cui periodo sia T = 1s, estrapoleremo ben 44100 valori/secondo. Sottoponendolo ad un’operazione di DFT, produrremo un numero di componenti frequenziali pari alla metà del numero di valori campionati +1, di cui la prima componente indicherà la componente continua del segnale (o valor medio), mentre l’ultima, il cui valore sarà nel nostro caso 22050, è detta frequenza di Nyquist, la cui definizione è:
Esiste un altro parametro importante: la risoluzione D f, definita come il rapporto tra la frequenza di campionamento e il n° dei campioni:
(13) ![]()
e rappresenta la spaziatura tra le righe dello spettro (fig. 8).
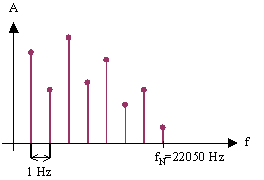
Fig.9
Per sistemi a segnale campionato si intendono quei sistemi come computer, DSP, ecc., utilizzati per effettuare l’analisi in bande di 1/3 d’ottava. Ad essi possono essere applicati anche segnali non periodici.
Si parte da un segnale campionato, che conosco quindi ad intervalli di tempo D t.
Introduciamo in primis un teorema fondamentale del campionamento, che la regola per la scelta della frequenza di campionamento:
TEOREMA DI SHANNON
"La frequenza di campionamento deve essere maggiore o uguale al doppio della frequenza massima contenuta nel segnale".
(14) ![]()
dove con fMAX si indica la frequenza massima contenuta nel segnale.
OSS.: il mancato rispetto di questo teorema si incorre nel fenomeno noto come ALIASING, cioè le componenti di suono a frequenza più elevate saranno sottocampionate e appariranno a frequenze più basse.
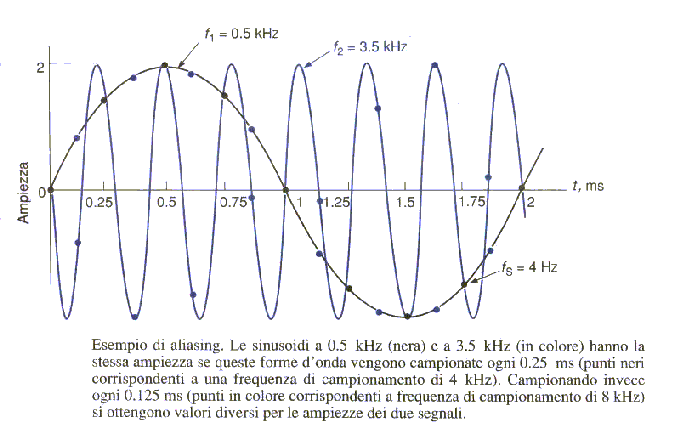
Fig. 10
All’aumentare della frequenza di campionamento, crescerà il numero di valori nell’unità di tempo; di conseguenza l’errore che commetterò sarà minore; questa considerazione è alla base del forte aumento delle frequenze di campionamento cui si è assistito negli ultimi anni per questo motivo in pochi anni le frequenze di campionamento sono aumentate notevolmente:
|
Dispositivo |
Frequenza di campionamento ( Hz ) |
|
CD – Compact Disc |
44100 |
|
DAT – Digital Audio Tape |
48000 |
|
DVD – Digital Video Disc |
96000 |
|
DVD Audio |
192000 |
L’utilità di frequenze di campionamento così elevate( 192 KHz , 96 KHz ) è discutibile almeno per quanto riguarda l'utilizzo acustico, perché il nostro sistema uditivo non è così sensibile.
Un sistema di campionamento classico è fatto così:
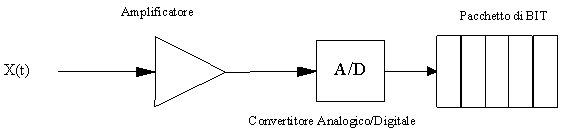
Fig.11-Campionatore
Il segnale analogico viene fatto passare attraverso un convertitore analogico/digitale che lo campiona trasformandolo in parole di n bit.
OSS. Campionare un segnale attraverso un sistema A/D comporta un’ulteriore perdita dell’informazione, poiché l’opera di discretizzazione non agisce solo lungo l’asse delle ascisse (tempo), ma anche lungo le ordinate (ampiezze), con un’ulteriore riduzione della qualità della conversione del segnale.
Quindi i convertitori A/D si caratterizzano sulla base dei seguenti parametri fondamentali:
I convertitori tipici, come i CD, hanno 16 bit ( signed integer, numeri con segno, cioè 65535 valori che vanno da –32767 a +32767) di livelli possibili in ampiezza mentre arrivano a frequenze di campionamento di 48000Hz.
I convertitori più moderni (le più evolute schede audio per P.C., DVD-A) hanno 24 bit di livelli e frequenze di campionamento a 96000Hz.
Fattori critici per il campionamento in campo musicale sono, piú che l’elevata frequenza di campionamento, la stabilità e il rapporto segnale – rumore, che dipende dal numero di bit utilizzati per la memorizzazione dei dati.
Ora il problema è quello di emulare la risposta di un filtro d’ottava o a frazioni di quest’ultima tramite un apparato digitale; una soluzione consiste nell’utilizzo di un filtro numerico, ossia un sistema che operi sui campioni del segnale mediante una formula matematica:
 Fig.12
Fig.12
In pratica i dati presenti all’ingresso del Blackbox vengono elaborati da una formula matematica che produce in uscita dei nuovi valori nella forma matematica che segue:
(15) ![]()
Una risposta ad un ingresso di questo tipo è caratteristica di una struttura chiamata FIR (Fined Impulse Response), cioè un filtro a risposta all’impulso finita.
OSS.: si definisce risposta all’impulso o funzione di trasferimento h(t) la risposta del sistema quando si presenta all’ingresso una Sequenza di Dirac, o delta di Dirac, che consiste nel valore "1" seguito da tanti "0", e risulta essere la sequenza dei coefficienti A0, A1,... , AN.
Il filtro di cui sopra ha una risposta all’impulso finita (nel tempo) perché in corrispondenza di un ingresso di una delta di Dirac l’uscita fornisce N campioni non nulli e poi degli zeri; per questo motivo, un filtro siffatto viene chiamato FIR.
Questo tipo di filtro non è molto potente, ma gode di un’importante proprietá: è stabile, cioè non si mette mai ad oscillare; inoltre, attraverso di esso, è possibile applicare qualunque tipo di filtraggio al segnale, a patto che N sia sufficientemente grande.
Per tanto l’utilizzo di una struttura di tipo FIR permette di calcolare i coefficienti del filtro, facendo in modo che lo stesso emuli la risposta in frequenza di un filtro d’ottava o di 1/3 d’ottava (sempre all’interno delle tolleranze prescritte dalle norme IEC).
Altra strada percorribile al fine di una soluzione del problema di emulare la risposta di un filtro d’ottava consiste nel ricorrere al cosiddetto filtro ricorsivo; esso presenta una struttura più complessa del caso FIR, e la sua risposta in un certo istante non dipende solo dall’ingresso in quello stesso istante ma anche dai valori d’uscita precedenti.
In forma matematica il concetto puó essere cosí espresso:
(16) ![]()
dove, in genere, ![]() . L’appellativo "ricorsivo" nasce dal fatto che i dati prodotti in uscita sono usati anche come parte dell’ingresso.
. L’appellativo "ricorsivo" nasce dal fatto che i dati prodotti in uscita sono usati anche come parte dell’ingresso.
Una struttura di questo tipo ha una risposta all’impulso infinita, cioè eccitando il filtro con una sequenza di Dirac l’uscita non andrà mai a zero. L’utilizzo di una struttura di questo genere richiede una certa attenzione inerente l’instabilità che si potrebbe verificare qualora i coefficienti Bi fossero molto grandi, poiché darebbe origine ad un fenomeno di autoalimentazione del filtro con segnali sempre più forti.
OSS.: abbiamo detto che un filtro IIR (Infinite Impulse Response) ha una risposta all’impulso infinita; in realtá essa tende asintoticamente a 0, e quindi ai fini pratici si può comportare come un filtro FIR, purché non sia instabile. In definitiva è un filtro piú efficiente di quello FIR, poiché con un ridotto numero di campioni produce un filtraggio migliore di quelli prodotti dai FIR; a patto di calcolare opportunamente i coefficienti Ai e Bi, un filtro IIR fornisce uscite stabili e risposte in frequenza all’interno delle tolleranze dettate dalle norme in vigore.
N.B.: gli analizzatori digitali usano filtri IIR.
5. APPROFONDIMENTO SULL’ANALISI DEI SEGNALI TRANSIENTI
L’analisi di segnali non stazionari non è in realtà un problema per dispositivi analogici tipo l’analizzatore di segnali transienti visto in precedenza (fig. 3), a patto di riuscire a memorizzare i dati abbastanza velocemente; se questo obiettivo viene centrato, si ottiene quello che si chiama un multispettro: una serie di spettri nel tempo. Esso è il risultato di un campionamento di valori istantanei dello spettro ogni un certo numero di ms.
Ora, proviamo a rispondere alla seguente domanda: è possibile ricorre alla analisi di Fourier nel caso di segnali transienti? Sotto il profilo strettamente teorico questo non sarebbe possibile, in quanto non è detto che un segnale transiente sia periodici. Utilizzando peró qualche artifizio è possibile adattare l’analisi di F. al nostro caso.
Il primo problema da risolvere è quello della continuità del segnale: infatti, analizzando una porzione di segnale formato da N campioni, può capitare che i valori d’inizio e di fine finestra non coincidano, quindi esso non risulta continuo con ala finestra successiva. Se il segnale poi fosse periodico, potrebbe capitare che la finestra di campionamento non coincida con il periodo del segnale stesso; questo perché il numero di punti di campionamento essere una potenza di 2 affinché il calcolo della trasformata discreta di Fourier sia veloce.
Ad esempio, nel caso di una sinusoide invece di ottenere una linea solo alla frequenza dell’onda stessa, otteniamo uno spettro che presenta energia a quasi le frequenze; questo perché ho in sostanza introdotto un gradino nel giuntare due finestre di campionamento successive. Questo fenomeno è detto Leaking, ed è dovuto proprio al fatto che la trasformata di Fourier ipotizza la periodicità del segnale ad N campioni.
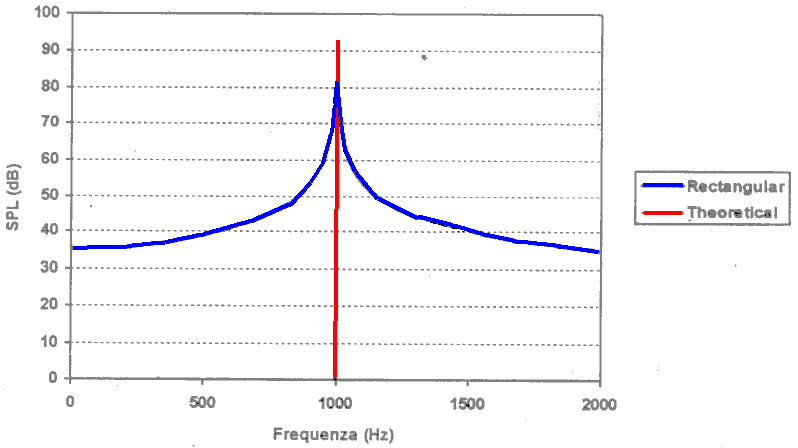
Fig.13 Effetto Laeking
Per ovviare a questo problema dobbiamo cercare di portare il segnale a zero agli estremi della finestra, applicando una sorta di filtro di copertura; in pratica si moltiplicano tutti i punti campionati per una funzione detta window , di durata pari al segmento di segnale da studiare, che annulla il segnale agli estremi..
Queste finestre vengono moltiplicate per il segnale in intervalli che si sovrappongono, cioè ad ogni passo si sposta la finestra verso il basso non di N campioni, ma di N/2, in modo che nessuna parte dell’onda venga completamente annullata e per questo tralasciata dall’analisi.:
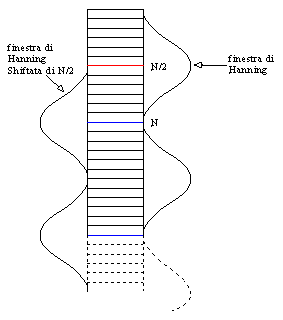
Fig.14
Esistono varie di queste finestre di uso frequente , di cui la più efficiente è la cosiddetta finestra Hanning , che non è altro che un coseno rialzato normalizzato ad uno. I singoli campioni vengono moltiplicati con le finestre Hanning , rimarranno quindi invariati al centro mentre agli estremi saranno portati a zero:
![]() cioè:
cioè:
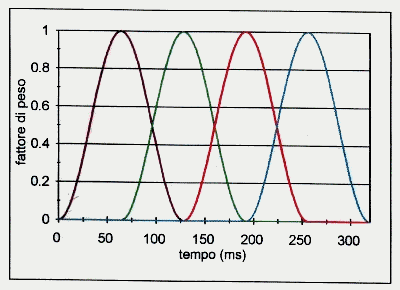
Fig.15
Quando si utilizzavano campionatori da 10 o 12 bit bande laterali da -70 dB non davano fastidio, mentre ora con convertitori a 24 bit e un rapporto segnale-rumore di 120![]() 130 dB questi lobi laterali non sono accettabili. Seguono ora degli esempi di multispettri nelle fig. 15 e 16, che rappresentano entrambe il sorvolo di un aereo. Si vede che sono possibili diversi tipi di visualizzazione; il sonogramma, nel quale il tempo è in ascissa , le frequenze in ordinata e i singoli spettri hanno l’ampiezza rappresentata dal colore. Oggi questo viene fatto via P.C. ma un tempo si utilizzava un apparecchio denominato sonografo.
130 dB questi lobi laterali non sono accettabili. Seguono ora degli esempi di multispettri nelle fig. 15 e 16, che rappresentano entrambe il sorvolo di un aereo. Si vede che sono possibili diversi tipi di visualizzazione; il sonogramma, nel quale il tempo è in ascissa , le frequenze in ordinata e i singoli spettri hanno l’ampiezza rappresentata dal colore. Oggi questo viene fatto via P.C. ma un tempo si utilizzava un apparecchio denominato sonografo.
Ecco un esempio di sonogramma:
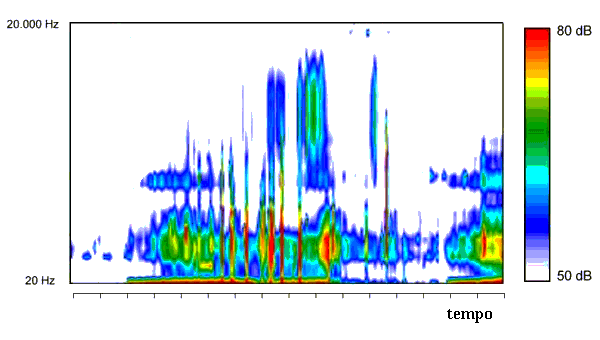
Fig.16
Altra rappresentazione è, come detto piú sopra, quella denominata waterfall (cascata): in essa sono messi in fila tanti spettri consecutivi nel tempo:
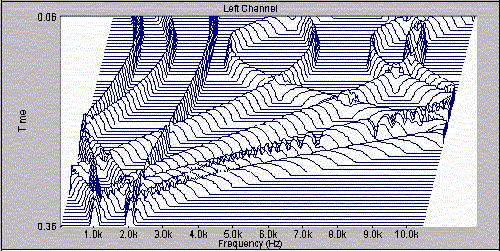
Fig.17