La propagazione del calore avviene secondo tre diverse metodologie: conduzione, convezione e irraggiamento. Nella convezione, modo di propagazione tipico dei fluidi, la propagazione del calore avviene con trasporto macroscopico di materia. Mentre nei fluidi si può avere anche trasporto di calore per convezione, il contrario non avviene mai nei solidi, nei quali la convezione non può aver luogo. La convezione, che costituisce il modo di trasporto di calore più sfruttato nelle applicazioni (basta pensare alle caldaie o agli impianti di riscaldamento centralizzati ) può essere naturale o forzata. Nel primo caso le porzioni di fluido più vicine alla sorgente di calore si dilatano diventando più leggere e meno dense di quelle sovrastanti. Le porzioni di fluido più calde prendono il posto di quelle più fredde e viceversa dando così luogo all’instaurarsi di una corrente fluida con trasporto di calore. Nel caso della convezione forzata, le correnti fluide sono provocate artificialmente e per effettuare il trasporto di calore è necessario compiere un lavoro esterno per mantenere le correnti nel fluido; generalmente alla convezione forzata si sovrappone la convezione naturale.

La quantità di calore scambiata, D Q, dalla superficie di un corpo solido e un fluido, in un tempo infinitesimo D t, dipende dall’area della superficie di contatto ,S, e dalla differenza di temperatura, D T, tra quest’ultima e il fluido.

In una prima approssimazione, secondo un’equazione dovuta a I. Newton, si può scrivere:

(1)

dove h è una costante detta coefficiente di convezione.; essa rappresenta la quantità di calore

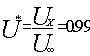(2) scambiata nell’unità di tempo tra la superficie unitaria e il fluido quando la differenza di temperatura tra essi è di 1°K.Notiamo che il termine coefficiente è impropriamente usato, in quanto esso indica una grandezza priva di dimensioni fisiche, mentre h ha dimensioni espresse nel S.I. di Watt al metro quadrato al grado kelvin :

Il coefficiente di convezione non è in realtà una costante, ma dipende da un numero molto grande di fattori, tra cui le caratteristiche del fluido e della corrente fluida, quali velocità, densità, comprimibilità, viscosità, dipendenti a loro volta dalla temperatura. Inoltre nello scambio termico possono diventare importanti anche fenomeni di cambiamento di stato del fluido per cui è impossibile dare un’espressione teorica di h; per la sua valutazione caso per caso si ricorre all’analisi dimensionale, un procedimento basato sulla similitudine.

Come detto in precedenza l’analisi dimensionale si basa su un procedimento chiamato di similitudine; prima di darne la definizione cerchiamo di capire, con un esempio, quando due esperienze possono essere catalogate come simili.

Prendiamo come prima esperienza lo scambio termico per convezione tra una parete a temperatura T_P , e l’aria circostante, che lontano dalla parete ha una temperatura di T¥ . (Fig.1)

Fig.1

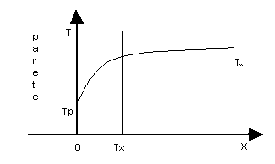
In figura viene mostrato l’andamento della temperatura in funzione della posizione del punto. In particolare T(0)=T_P è la temperatura di un punto sulla superficie del corpo, mentre T¥ (che è maggiore di T_P ) indica la temperatura del fluido lontano dalla parete. L’ascissa T_X è chiamata strato limite termico, ed è per definizione il luogo dei punti in cui è avvenuto il 99% del salto di temperatura. La potenza termica scambiata per unità di superficie è calcolabile attraverso l’espressione:

(3)

In questa esperienza diventa possibile definire una temperatura adimensionale T^* , indipendente dai parametri finora adottati, che permette di calcolare direttamente lo strato limite termico:

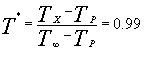(4) La seconda esperienza tratta di un problema di fluidodinamica, in particolare cerchiamo di studiare la variazione della velocità di un fluido, come ad esempio l’aria, in prossimità di una parete, dove si verificano fenomeni di aderenza. (Fig. 2)

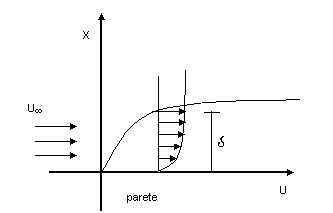
Fig.2

Il grafico mostra l’andamento della velocità dell’aria in funzione della posizione del punto rispetto all’ascissa X, che per comodità è indicata sull’asse verticale. La velocità iniziale dell’aria è U¥ , mentre la velocità U_X indica la velocità locale. d viene chiamato strato limite fluidodinamico, e rappresenta lo strato nel quale avviene il 99% del salto di velocità dell’aria. Anche in questa esperienza è possibile definire una velocità adimensionale, U* , che permetto di calcolare direttamente lo strato limite fluidodinamico :

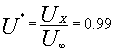(5)

La tecnica utilizzata in entrambi gli esperimenti è chiamata analisi dimensionale e consiste nella creazione di variabili adimensionali, che rendono le equazioni invariati rispetto alle grandezze fisiche in gioco. I due problemi sono stati resi simili grazie alle manipolazioni fatte alle grandezze fisiche. La potenze di questa metodologia di studio dei problemi fisici è ormai comprensibile: la soluzione di un problema in un campo della fisica è soluzione in qualsiasi campo di problemi simili a quello studiato. Per catalogare due problemi come simili si può utilizzare il teorema della similitudine, che nella teoria dei modelli meccanici afferma la seguente proposizione:

condizione necessaria e sufficiente perché tra due sistemi sussista una similitudine è che esista la possibilità di determinare due sistemi di unità di misura tali che le grandezze che intervengono nel fenomeno che si considera siano misurate dagli stessi numeri puri nei due sistemi.

Anche se la teoria mostra, per la loro complessità, una varietà infinita di esperienze, nella pratica quotidiana i problemi, la cui soluzione è fondamentale per le discipline ingegnieristiche, sono in numero limitato. I 30-35 problemi fondamentali sono stati studiati attraverso specifici esperimenti, in quanto la loro risoluzione algebrica era, ed è tutt’oggi, molto complessa. Trovata la soluzione per via empirica i problemi sono state tabulati e divisi in classi secondo la loro geometria (parete piana, sfera, tubo cilindrico …),densità e velocità di moto (moto laminare, moto turbolento) , ed altre caratteristiche fondamentali, in modo da poter essere utilizzati come problemi tipo. Una parte della ricerca scientifica studia tutt’oggi i problemi che per le loro caratteristiche non possono essere resi simili ai problemi fondamentali già studiati.

Ma quante variabili adimensionali dobbiamo utilizzare per risolvere un problema di scambio termico?

In questo tipo di problema le variabili in gioco sono tante; calore, temperatura, dimensioni spaziali, tempo, densità e viscosità del fluido, sono solo alcune delle grandezze da studiare. Per sapere quante variabili adimensionali dobbiamo utilizzare nel nostro problema è opportuno utilizzare il teorema di Buckingham:

Il numero di parametri adimensionali necessari per descrivere compiutamente un fenomeno fisico, è dato dal numero di variabili che descrivono il problema meno il numero di relazioni che legano le variabili stesse.

Nei problemi di scambio termico il numero di parametri adimensionali N_AD da considerare è quattro.

I quattro parametri utilizzati per descrivere un fenomeno di scambio termico sono solitamente :

Mentre i coefficienti di Reynolds, Grashof e Prandtl, sono già stati descritti in questo corso, il posizionatore è un nuovo parametro adimensionale di fondamentale importanza nei problemi di scambio termico. Il posizionatore è il rapporto tra il vettore spaziale (nei problemi monodimensionali è la coordinata del punto ), e la lunghezza caratteristica.

Quest’ultima può essere il diametro di un tubo, la superficie di una parete, il raggio di una sfera.

La lunghezza caratteristica va presa con senso fisico e la sua scelta è delicata e non banale. Se il problema in esame è figlio di un’esperienza già studiata, è necessario adottare la stessa lunghezza caratteristica utilizzata per trovare la soluzione del problema tipo, altrimenti bisogna studiare bene la geometria del problema.

Un esempio di come cambia la scelta della lunghezza caratteristica per problemi di diversa geometria è lo studio della dispersione termica di un cilindro sul quale viene forzatamente soffiata aria. Se l’aria viene soffiata lateralmente sul cilindro( Fig.3 ) , è opportuno scegliere come lunghezza caratteristica il diametro del cilindro. Diversa è la scelta se l’aria viene soffiata longitudinalmente ( Fig.4 ); in questo caso è necessario prendere come lunghezza caratteristica la lunghezza vera e propria del cilindro.

Fig.3 Fig.4

Terminata l’analisi del posizionatore, diamo uno descrizione degli altri tre numeri puri, in un problema di scambio termico per convezione.

Nel numero di Reynolds,

(6)

w indica la velocità con cui il fluido viene spinto contro la parete; se la convezione è naturale la velocità del fluido viene assunta uguale a zero. Al denominatore, n indica la viscosità del fluido, ed L la lunghezza caratteristica già analizzata.

Il numero di Grashof,

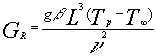(7)

è direttamente proporzionale all’accelerazione di gravità g, al coefficiente di dilatazione termica b , al cubo della lunghezza caratteristica L , alla differenza di temperatura tra la parete ed il fluido lontano da essa T_P - T¥ , ed è inversamente proporzionale al quadrato della viscosità cinematica n .

Notiamo che b ha dimensioni fisiche dell’inverso della temperatura assoluta. Infatti ricordando che

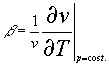(8)

quando diminuisce la densità la densità e il gas può essere considerato un gas perfetto,

(9)

da cui si ricava

(10)

Il numero di Prandtl,

(11)

è direttamente proporzionale alla viscosità del fluido n ed inversamente proporzionale alla sua diffusività termica a ².

In tutti i casi lo studio del problema viene trattato con le grandezze fisiche del fluido, fatta eccezione per la temperatura di parete.

Dall’analisi dei quattro coefficienti trovati dobbiamo ricavare il coefficiente di convezione h. Per fare questo ci serviamo di un coefficiente di convezione adimensionale chiamato numero di Nusselt, direttamente proporzionale al coefficiente di convezione secondo la formula,

(12)

nella quale l indica la conducibilità del fluido. Notiamo come il numero di Nusselt ha la stessa espressione del numero di Biot, con la differenza che se nel numero di Biot la conducibilità espressa si riferiva a quella della parete, nel numero di Nusselt si riferisce al fluido.

Il numero di Nusselt è funzione dei numeri puri di Reynolds, di Grashof, di Prandtl, e del posizionatore

.

(13)

La funzione che restituisce il numero di Nusselt a partire dai quattro numeri puri deve essere unica ed a coefficienti costanti, ed è chiamata soluzione del problema.

Dato un certo campo di validità dei risultati ( es. A < R_E < B, C < P_R < D, … ) si cerca la formula attraverso mirate esperienze. Alcune soluzioni sono molto usate e note. Un esempio è la formula di Dittus-Boelter, utilizzata per calcolare lo scambio termico di un fluido in un tubo cilindrico (vedi tab.1). In alcuni casi la soluzione del problema può essere trovata attraverso esperienze diverse in campi di validità diversi, e può dare risultati diversi che differiscono del 20-30% dal loro valore reale; in questi casi si può trovare un risultato più corretto mediando i valori trovati da più esperienze.

Per prima cosa dobbiamo metterci nella logica di chi usa il lavoro fatto da altri, ovvero dato un problema qualunque è bene ricercare un problema simile e adottarne le convenzioni. Solo in seguito si può procedere nella ricerca della soluzione.

Dopo lo studio e l’analisi di alcuni casi si è potuto generalizzare la struttura della soluzione del problema:

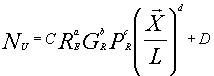(14)

La struttura è simile ad un’analisi dimensionale, se si esclude il coefficiente D che in effetti appare solo in rari casi. Gli esponenti a,b,c,d, e la costante correttiva C devono essere determinati caso per caso in funzione delle condizioni e dei campi di validità del problema. Nelle tabelle 1 e 2 vengono mostrate caso per caso le esperienze già risolte e la loro corrispondente soluzione.

Esistono due categorie di problemi nei quali il numero di Nusselt è indipendente dal coefficiente di convezione, e scompare la dipendenza spaziale, d=0:

1. Aspettare che il regime del fluido si sia completamente sviluppato, come nel problema risolto

da Dittus e Boelter.

2. Quando lo scambio di calore non è omogeneo, cioè fluido e parete hanno quantità di calore

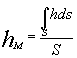(15)

Per stabilire quale formula utilizzare nel caso di convezione forzata o naturale, ci serviamo come descrittore dello stato del fluido del rapporto tra il numero di Grashof e il quadrato del numero di Reynolds. Noto che il numero di Grashof descrive la convezione naturale, e il numero di Reynolds quella forzata, il loro rapporto può essere:

1)

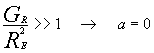La convezione è naturale, sono preponderanti le forze di galleggiamento definite da G_R.

Possiamo quindi assumere che nella formula (14) l’esponente a sia nullo.

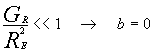2)

La convezione è forzata. Le forze di galleggiamento sono trascurabili perché la densità del fluido subisce piccole variazioni, o perché le forze esterne sovrastano la condizione di convezione naturale. Possiamo, in analogia con quanto fatto prima, considerare nullo l’esponente b, in modo da eliminare dalla (14) il numero di Grashof che indica convezione naturale.

3)

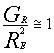La convezione è mista e il problema può essere risolto con l’analisi di entrambi i casi.

I problemi in cui il fluido è in condizione di convezione forzata, sono più facilmente risolubili, infatti una volta ottenuta la velocità fluidodinamica si può calcolare lo scambio termico. Nella convezione naturale il problema è più complesso perché la velocità del fluido e lo scambio termico sono uno funzione dell’altro.

In convezione naturale la (14) diventa

(16)

che uguagliata alla (12) restituisce il valore del coefficiente di convezione in funzione del numero di Grashof e del numero di Prandtl.

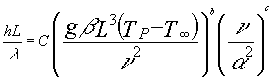(17)

Notiamo che se b=1/3 il coefficiente di convezione non dipenderebbe più dalla lunghezza caratteristica. Nella gran parte dei problemi di convezione naturale accade proprio questo, cioè lo scambio termico non dipende dalla superficie di scambio. Se b>1/3 lo scambio termico si vivacizza al crescere delle dimensioni della superficie di scambio, questo è tipico della convezione forzata.

Lo scambio termico attraverso un gas perfetto, ad esempio l’aria, è leggibile nella formula se b=c.

Il numero di Grashof ed il numero di Prandtl si moltiplicano dando come risultato il numero di Raleigh:

Il numero di Nusselt diventa così direttamente proporzionale al numero di Raleigh e ad una costante C.

(18)

Il coefficiente costante C è funzione della superficie di scambio e delle temperature di fluido e parete. Il suo valore varia in questo modo:

1- Quando la superficie di scambio ( pavimento ) è sotto il fluido ed è più calda di esso, oppure la superficie ( soffitto ) è sopra il fluido ma ha una temperatura inferiore, si formano correnti convettive ed il valore del coefficiente è

C=0.14

2-Quando il pavimento ha una temperatura inferiore al fluido, oppure il soffitto ha una temperatura superiore, il fluido tende a stratificarsi, e il coefficiente vale

C=0.07

3-Se la parete è verticale, indipendentemente dalle due temperature

C=0.13

Cerchiamo ora di riassumere le tutte le informazioni raccolte.

Per determinare il coefficiente di convezione è necessario trovare la soluzione del problema in modo da eguagliare il numero di Nusselt ottenuto con la formula (12). La soluzione del problema va ricercata in una serie di soluzioni note raccolte nelle tab.3-4. Le esperienze hanno diverse validità di campi e si diversificano principalmente in quattro categorie: problemi di convezione naturale o forzata, e regime del fluido laminare o turbolento. Le quattro categorie sono riassunte in Tab.1.

Tab.1

La maggioranza dei problemi di interesse, e quindi studiati, sono quelli evidenziati in tabella dalla diagonale. Il tipo di convezione del problema da risolvere deve essere noto, ed è comunque comprensibile dall’analisi dei dati. Il regime del fluido è invece da determinare.

Se stiamo lavorando su un’esperienza di convezione forzata abbiamo a disposizione del numero di Reynolds, che come è ben noto, è un descrittore del regime del fluido.(Tab.2)

Tab.2

Quando invece lavoriamo su esperienze di convezione naturale non è implicita la conoscenza del numero di Reynolds. Per determinare il regime del fluido dobbiamo affidarci ad un altro descrittore, e l’unico che è in grado di sostituire il numero di Reynolds è il numero di Raleigh, che assume così un’importanza fondamentale per la ricerca della soluzione del problema.(Tab.3)

Tab.3

Noti il tipo di convezione, il regime del fluido, e i campi di validità delle grandezze in gioco è possibile ricercare nelle tabelle 4-5 la soluzione del problema.

Formule sperimentali per il calcolo del numero di Nusselt: CONVEZIONE FORZATA

Tab.4

Formule sperimentali per il calcolo del numero di Nusselt: CONVEZIONE NATURALE

Tab.5