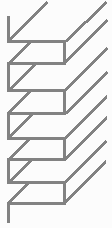
Superfici alettate

fig.1
Durante la progettazione e costruzione di strutture di vario genere si rende spesso necessario considerare il raffreddamento delle stesse, per ragioni che dipendono dal loro utilizzo.
Uno dei metodi più comuni di ottenere un soddisfacente scambio termico per mezzo dell’aria è quello di prevedere lastre di materiale non liscie ma contenenti numerose "alette", cioè bordi sporgenti allo scopo di aumentare la superficie preposta allo scambio termico(vedi fig.1).
Le alette possono essere realizzate direttamente sulla lastra di materiale oppure costruite a parte e montate successivamente.
Le superfici alettate hanno molti differenti campi di applicazione, dal raffreddamento dei transistor alle batterie dei condizionatori e dei radiatori delle automobili; si caratterizzano per guadagno ed efficienza.
Esistono vari tipi di alette, di seguito sono raffigurati i profili di due fra i modelli più comuni:

Aletta lineare (molto utilizzata)

Aletta rastremata (molto efficiente ma poco pratica a causa della difficoltà di calcolo dei parametri)
L’aletta viene costruita con un materiale la cui conducibilità l ne determina la temperatura, che non sarà uniforme; essa andrà decrescendo allontanandosi dalla "base" dell’aletta.
Si capisce, quindi, che esiste una lunghezza ottimale, che permetterà il massimo scambio termico, oltre la quale interverranno fenomeni collaterali come ad esempio la "frenatura" dell’aria, causa di un decremento delle capacità di raffreddamento dell’aletta.
Per semplificare i conti noi trascureremo l’effetto frenante dovuto all’aria.
 x
x
|
x x + dx L |
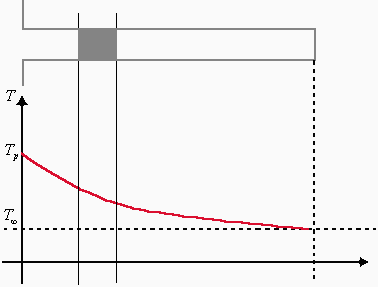
fig.2
In fig.2 abbiamo indicato con T¥ la temperatura ambiente, e abbiamo trascurato l’effetto della testa dell’aletta nel processo di scambio termico, approssimazione valida nel caso in cui l’aletta sia molto lunga e stretta.
Ora è necessario determinare l’espressione di T(x) per capire come avviene lo scambio di calore tra aletta e ambiente.
Supponiamo che esista una resistenza termica di contatto, Rc, nel punto in cui la base dell’aletta si innesta sulla lastra piatta; tale resistenza assume un’importanza notevole nel caso di alette riportate, cioè montate sulla lastra in momento successivo sua alla fabbricazione.
La resistenza Rc determina un "gradino", una caduta iniziale di temperatura, il cui gradiente influisce sulla densità del flusso di calore, indebolendolo.
Per la trattazione analitica del fenomeno consideriamo elementi infinitesimi del flusso di calore entranti ed uscenti da un generico volumetto preso all’interno dell’aletta:
|
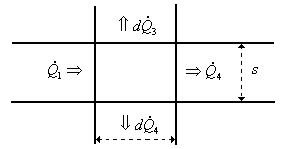
dx fig.3 |
L’elemento di volume scambiando calore in ogni direzione permette di scrivere un bilancio, ricordando che i flussi scambiati verticalmente sono proporzionali a dx, sono convettivi e uguali per simmetria:
|
|
ricordando inoltre l’espressione che lega densità di flusso di calore e gradiente di temperatura:
|
|
da cui, derivando ambo i membri rispetto a x:
|
|
per ottenere una formula che esprima il flusso totale in funzione del gradiente di temperatura occorre moltiplicare per lo spessore dell’aletta, "s":
|
|
|
|
|
|
Per mezzo della sostituzione indicata possiamo ricondurci alla nota equazione di Helmoltz, vista in acustica:
|
|
|
|
La cui soluzione, nota, è:
|
|
A e B sono parametri da determinare in base alle condizioni al contorno:
|
x = 0 , x = L |
La soluzione trovata differisce da quella ricavata in ambito acustico poiché il termine m**2 aveva segno negativo, e di conseguenza si ottenevano radici complesse.
Pertanto ora la soluzione non sarà più costituita da un termine oscillante, ma da un termine smorzato asintotticamente; esiste un valore critico di smorzamento, che determina l’oscillazione del sistema se raggiunto. In questo caso la temperatura cala senza oscillare.
Se non ci fosse Rc per x = 0 avremmo esattamente J = (Tp - T¥ ), mentre invece:
Per x = 0 :
|
|
Per x = L :
|
|
Questo risultato è dovuto al fatto che oltre la punta non è presente alcun flusso.
Ora è possibile ricavare A e B:
|
|
|
|
Sostituiamo le espressioni ricavate per A e B nell’equazione di J :
|
|
Per sapere quali benefici ha portato la presenza dell’aletta calcoliamo i flussi di calore nei due casi:
|
|
|
|
Dove le due equazioni ricavate si riferiscono al flusso in caso di parete liscia (p), e al flusso presente sulle facce dell’aletta. Sostituendo nella seconda (T(x) - T¥ ):
|
|
Il rapporto tra i due flussi così ottenuti è detto guadagno dell’aletta ( ³ 1 ):
|
|
Il guadagno raggiunge un massimo nel caso in cui l’aletta abbia temperatura uniforme pari a Tp; l’espressione del flusso sull’aletta diventerebbe allora:
|
|
Questa considerazione suggerisce l’introduzione di un secondo importante parametro di caratterizzazione delle alette, l’efficienza ( £ 1 ), definita come il rapporto tra il flusso di calore sull’aletta in caso di temperatura decrescente e il flusso massimo:
|
|
Sostituendo l’espressione di e in quella del guadagno si trova una utile relazione tra i due parametri:
|
|
Da cui si può notare come per aumentare il guadagno, a parità di efficienza, sia consigliabile costruire alette lunghe e sottili.
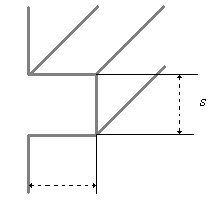
Caso limite ( L = s )
|
L fig.4 |
Un’aletta del tipo specificato in fig.4 rappresenta un caso particolare in quanto l’espressione del guadagno ricavata in precedenza assumerebbe il seguente valore, cosiderando efficienza unitaria:
|
|
In realtà il guadagno dovrebbe essere pari a 3, dal momento che rispetto alla lastra piana si ha un incremento di superfici da una a tre. Questo errore è dovuto al fatto di aver trascurato la "testa" dell’aletta nel ricavare la formula del guadagno. Per correggere tale errore è necessario quindi considerare la superficie ignorata in precedenza, riportando metà della sua superficie sulla faccia superiore dell’aletta, e l’altra metà sulla faccia inferiore, come in fig.5:
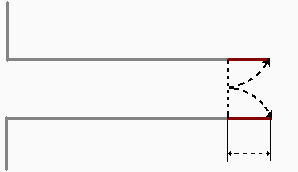
|
s/2 |
|
fig.5 |
Per mezzo di questo artificio è possibile riscrivere l’espressione del guadagno utilizzando la lunghezza L’ che risulta composta dalla lunghezza efettiva dell’aletta e dal termine aggiuntivo s/2 relativo allo spessore della stessa.
|
|
|
|
Si è indicato con ea l’efficienza della singola aletta; è interessante trovare il valore della e tot relativa all’intero sistema di alette. Per fare questo è necessario valutare la potenza termica totale:
|
|
Dove la densità di flusso della superficie piana (scambiata dalla lastra dove non sono presenti alette) è ricavabile dalla formula:
|
|
Mentre la densità di flusso delle alette si trova ricordando l’equazione del guadagno:
|
|
In queste formule si è indicato con Stot la superficie totale della lastra senza alette, e con Sal la superficie occupata dalle alette, ovvero la porzione di Stot su cui si innestano le basi delle alette.
Quindi riscrivendo l’espressione del flusso totale avendo sostituito le densità di flusso ricavate, si ottiene:
|
|
E' ora possibile, sfruttando questo risultato, scrivere una formula per il guadagno totale del sistema:
|
|
Allo stesso modo si può ottenere l’espressione dell’efficienza totale ( basta dividere il flusso totale per il flusso totale dove e a = 1 ):
|
|
Solitamente i parametri caratteristici delle alette ( e , G ) vengono forniti dal costruttore.
Riportiamo a seguito alcune tabelle che mostrano il rendimento di vari tipi di alette:
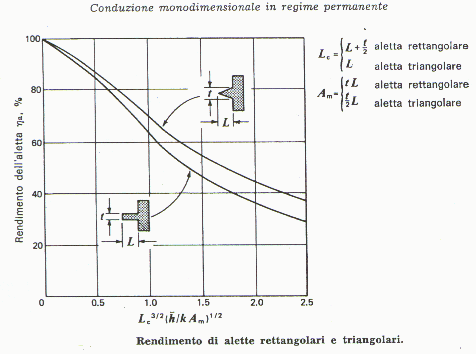
fig.7
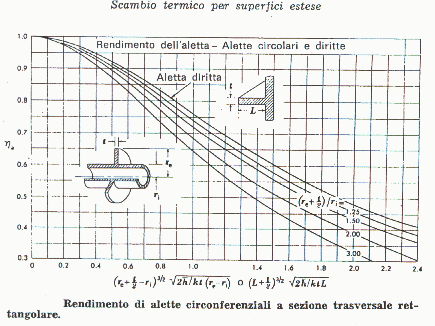
fig.8
Esercizio
( raffreddamento di una CPU )Si consideri la CPU di un computer, posta a contatto con una lastra quadrata di lato pari a 50mm. Tale lastra deve smaltire una potenza di 20W, con una temperatura di parete pari a 100° C e una temperatura ambiente di 20° C. Progettare una superficie alettata nel caso in cui tale lastra non sia sufficiente a raffreddare la CPU.
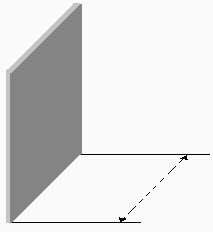 L = 50 mm Tp = 100° C T¥ = 20° C
L = 50 mm Tp = 100° C T¥ = 20° C
Calcoliamo innanzitutto i numeri di Grashof e Prandtl( quest’ultimo vale sempre 0.71 per l’aria), per trovare una formula adeguata che permetta di ricavare il numero di Nusselt:
|
|
Pr = 0.71
|
|
Siamo in presenza di convezione naturale con un numero di Rayleigh compreso minore di 10**9, di conseguenza la formula da utilizzare è quella di McAdams:
|
|
|
|
Dobbiamo ora considerare la quota di flusso termico dovuto all’irraggiamento:
|
|
|
|
Troviamo a questo punto la temperatura massima che raggiungerà la lastra a contatto con la CPU:
|
|
Una temperatura tanto alta causerebbe sicuramente danni al processore, pertanto progettiamo una superficie alettata adatta al nostro problema.
Supponiamo di applicare alla nostra CPU una superficie su cui sono montate otto alette lunghe 20mm, spesse 3mm, con una distanza fra una e l’altra di 3mm.
Consultando una tabella troviamo:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Questo valore di temperatura è adatto allo scopo per cui si era reso necessario progettare la superficie alettata.