Schema 1
Obiettivi della lezione
Analizzare il fenomeno delle onde stazionarie, gli effetti che produce su grandezze quali l’impedenza, l’intensità sonora; capire come sfruttare le onde stazionarie per determinare il coefficiente di assorbimento acustico di un generico materiale, mediante alcune apparecchiature e strumenti di misura.
Definire la densità di energia sonora e impiegarla nel calcolo del coefficiente di assorbimento acustico.
Il tubo ad onde stazionarie
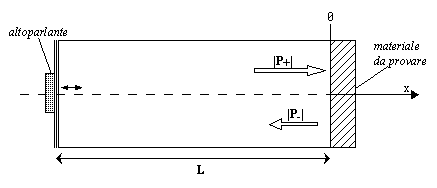
Detto anche "tubo di Kundt", serve a misurare l'impedenza e il coefficiente di assorbimento acustico (grandezza derivata dell'impedenza) di un campioncino di materiale. Nella figura sottostante è schematizzato nelle sue parti fondamentali:

Schema 1
Tale apparato è costituito da un tubo, in una estremità del quale è collocato un altoparlante (o un pistone) che ha lo scopo di generare un treno di onde piane progressive che si propaghino all'interno del tubo; l'altra estremità del tubo termina con un oggetto, un campioncino costituito da un pezzo del materiale di cui vogliamo determinare impedenza e coefficiente di assorbimento acustico.
In corrispondenza di questo "tappo" di materiale l’impedenza locale assumerà un determinato valore calcolabile tramite la formula:
![]() (1)
(1)
dove P e v si riferiscono a valori istantanei di pressione e velocità.
Osservazione: l’impedenza è in generale una grandezza complessa, poichè niente garantisce che pressione e velocità siano tra loro in fase sulla superficie del materiale (dipende in che misura lo stesso è poroso, cedevole, flessibile ecc.).
Per compiere le misure che ci siamo prefissati, è importante che sulla terminazione del tubo giunga un’onda piana progressiva il più perfetta possibile, ovvero il campo sonoro deve essersi allontanato "sufficientemente" dalla sorgente. Sufficientemente significa prevedere una lunghezza del tubo molto maggiore della lunghezza dell’onda piana che intendiamo generare: ![]() (dove L è la lunghezza del tubo). Inoltre ci serviamo di un sistema di riferimento lineare e poniamo l’origine in corrispondenza del bordo interno del campioncino di materiale, per comodità di calcoli. Queste scelte sono rappresentate graficamente nello Schema 1 della pagina precedente.
(dove L è la lunghezza del tubo). Inoltre ci serviamo di un sistema di riferimento lineare e poniamo l’origine in corrispondenza del bordo interno del campioncino di materiale, per comodità di calcoli. Queste scelte sono rappresentate graficamente nello Schema 1 della pagina precedente.
Il fenomeno delle Onde Stazionarie
Sotto le condizioni prodotte all’interno del tubo, si manifesta il fenomeno delle onde stazionarie: l’onda piana che arriva sul materiale viene riflessa e torna indietro; nel tubo viaggia un treno d’onda incidente (generato da noi) che si va a sovrapporre a un treno d’onda riflesso (dal materiale).
In altre parole, la sovrapposizione tra il campo sonoro progressivo (verso le x positive) e il campo regressivo (nel verso delle x negative) produce l’onda stazionaria.
Dal punto di vista analitico, è necessario prendere in considerazione sia la soluzione positiva che quella negativa dell’equazione di D’Alambert, per via delle ipotesi appena esposte. Questo significa che il potenziale della velocità ![]() è costituito da due componenti
è costituito da due componenti ![]() e
e ![]() che danno origine a due velocità di verso opposto:
che danno origine a due velocità di verso opposto:
![]() (2)
(2)
Se ipotizziamo un’eccitazione di tipo sinusoidale, allora possiamo raccogliere il fasore ![]() e riscrivere il potenziale della velocità come:
e riscrivere il potenziale della velocità come:
![]() (3)
(3)
Osservazione: in alcuni testi i termini fasoriali ![]() vengono sottintesi, poichè comuni a tutte le grandezze che si stanno trattando; tuttavia, tale omissione può confondere le idee riguardo al significato fisico di ciascuna formula.
vengono sottintesi, poichè comuni a tutte le grandezze che si stanno trattando; tuttavia, tale omissione può confondere le idee riguardo al significato fisico di ciascuna formula.
Calcolo dell'impedenza
Dall’espressione del potenziale di velocità si può ricavare la velocità stessa; inoltre, tramite l’equazione di Eulero si può ricavare anche la pressione:
![]() (4)
(4)
![]() (5)
(5)
I termini ![]() e
e ![]() sono costanti di integrazione: per determinarli occorrono due condizioni al contorno. Una può essere la condizione di generazione: nel punto x = -L io conosco la legge del moto e quindi posso conoscere il valore di velocità di quel punto. La seconda condizione si può considerare in corrispondenza del punto x=0: in tal caso non conosco a priori il valore di velocità, ma posso ricavarlo tramite la (1) dall’impedenza, che in x=0 assumerà un ben determinato valore. Infatti posso legare la velocità alla pressione derivando quest’ultima rispetto ad x:
sono costanti di integrazione: per determinarli occorrono due condizioni al contorno. Una può essere la condizione di generazione: nel punto x = -L io conosco la legge del moto e quindi posso conoscere il valore di velocità di quel punto. La seconda condizione si può considerare in corrispondenza del punto x=0: in tal caso non conosco a priori il valore di velocità, ma posso ricavarlo tramite la (1) dall’impedenza, che in x=0 assumerà un ben determinato valore. Infatti posso legare la velocità alla pressione derivando quest’ultima rispetto ad x:
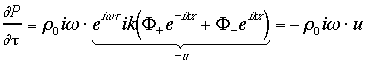 (6)
(6)
E’ interessante ricavare da questa equazione l’espressione della velocità e confrontarla con quella data dall’equazione di Eulero:
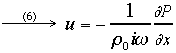 e
e 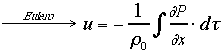 ;
;
Questo evidenzia una proprietà di ogni grandezza fasoriale, per la quale eseguirne l’integrale nel tempo equivale a dividerla per ![]() : è un filtraggio che attenua il segnale al crescere della frequenza, ovvero raddoppiando la frequenza si dimezza l’ampiezza (nella pratica questo equivale a un filtro passabasso con funzione di trasferimento la cui pendenza sia 6db/ottava).
: è un filtraggio che attenua il segnale al crescere della frequenza, ovvero raddoppiando la frequenza si dimezza l’ampiezza (nella pratica questo equivale a un filtro passabasso con funzione di trasferimento la cui pendenza sia 6db/ottava).
L’importanza di questo risultato consiste nel poter determinare la velocità (a partire dal gradiente di pressione) senza dover calcolare un vero integrale, ma realizzando una semplice equalizzazione del segnale di pressione: in altre parole basta passare attraverso un circuito elettrico analogico che progressivamente tolga ampiezza al segnale tanto più questo si presenta con frequenza elevata.
La soluzione trovata per il campo di pressione, tuttavia, non è molto soddisfacente, a causa della presenza dei termini ![]() e
e ![]() che non sono di facile calcolo e che comunque richiedono l’imposizione delle condizioni al contorno.
che non sono di facile calcolo e che comunque richiedono l’imposizione delle condizioni al contorno.
L’ideale sarebbe definire un’espressione formalmente simile alla precedente, dove tuttavia compaia la sovrapposizione di una pressione incidente di modulo |P+| e di una pressione riflessa di modulo |P-| (si veda lo Schema 1 a pag.1), al posto dei potenziali di velocità, ovvero:
![]() (7)
(7)
Considerando per un momento che dentro il tubo esista la sola onda di pressione che procede verso il materiale, ossia P+, si possono adoperare le relazioni già ricavate nel caso generico delle onde piane progressive per calcolare l’onda di velocità incidente conoscendo l’onda di pressione. Analogamente considerando che ci sia solo l’onda riflessa identificata da P-, anche per essa potrei calcolare il campo di velocità riflessa in funzione del campo di pressione riflesso.
Questo modo di procedere presuppone l’ipotesi di sovrapponibilità degli effetti; in altre parole deve essere fisicamente vero che il campo sonoro nel tubo sia la somma algebrica del campo della sola onda incidente e della sola onda riflessa.
Tale ipotesi è lecita e verificata in acustica lineare (fino a un limite di circa 160dB, un livello sonoro difficilmente raggiungibile dalle comuni sorgenti con cui si opera): questo significa che io posso scomporre un campo acustico comunque complesso in diverse componenti e studiarle separatamente; in questo caso specifico del tubo ad onde stazionarie, è possibile ragionare distintamente sulla componente incidente e su quella riflessa del campo sonoro totale.
Quindi, sfruttando le relazioni tra P ed u per le onde piane progressive, posso riscrivere l’espressione della velocità complessiva in questo modo:
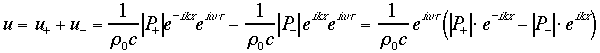 (8)
(8)
Nella somma di velocità compare il segno meno: infatti la velocità è una grandezza vettoriale e in questo caso le due componenti addende sono opposte e quindi algebricamente si sottraggono .
Ora ho tutto ciò che mi occorre per ricavare l’impedenza:
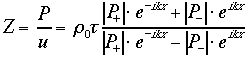 (9)
(9)
è importante notare che il valore dell’impedenza varia sensibilmente rispetto ad x, ovvero al punto dove ci si trova lungo il tubo: non è più vero (come era nelle onde piane progressive) che ![]() dappertutto. Tale impedenza variabile è originata dall’interferenza tra l’onda incidente e quella riflessa.
dappertutto. Tale impedenza variabile è originata dall’interferenza tra l’onda incidente e quella riflessa.
Inoltre, siccome l’impedenza è data da un rapporto complesso, a seconda di come si dispongono le fasi delle grandezze al numeratore e al denominatore, ci saranno delle zone dove essa assumerà un valore massimo e altre zone dove il valore sarà minimo; in particolare, quando i fasori ![]() e
e ![]() assumono fase identica (si allineano sul piano di Gauss) i segnali si combinano dando luogo alla massima impedenza. Viceversa, quando si verifica l’opposizione di fase, i due segnali si annientano originando una condizione di impedenza minima.
assumono fase identica (si allineano sul piano di Gauss) i segnali si combinano dando luogo alla massima impedenza. Viceversa, quando si verifica l’opposizione di fase, i due segnali si annientano originando una condizione di impedenza minima.
Nel caso in cui ![]() l’impedenza varia tra 0 e infinito; tuttavia questa condizione non è realistica, perchè ogni materiale produce sempre un po’ di attenuazione del segnale (
l’impedenza varia tra 0 e infinito; tuttavia questa condizione non è realistica, perchè ogni materiale produce sempre un po’ di attenuazione del segnale (![]() ), ossia il campo riflesso è più debole e quindi l’impedenza fluttua tra valori finiti e non nulli.
), ossia il campo riflesso è più debole e quindi l’impedenza fluttua tra valori finiti e non nulli.
Definiamo il "rapporto complesso di riflessione" , CRF, nel modo seguente:
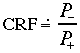 (10)
(10)
Si può esprimere l’impedenza in funzione del CRF in un punto particolare: sulla pelle del materiale, x =0, laddove è noto il valore complessivo dell’impedenza (perchè l’impedenza del campo in quel punto eguaglia l’impedenza del materiale):
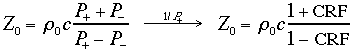 (11)
(11)
Supponiamo ora di non conoscere l’impedenza del materiale, ma di poterla misurare per poi ricavare il valore di CRF: a questo scopo rimaneggiamo la formula (11) per ottenere la seguente:
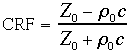 (12)
(12)
Questa espressione è molto importante perchè lega il rapporto tra le pressioni incidenti e riflesse con il valore dell’impedenza del materiale che si trova a terminare il tubo.
Analisi delle intensità e calcolo del coefficiente di assorbimento
Anche dal punto di vista energetico supponiamo valida la teoria della sovrapponibilità degli effetti, quindi possiamo identificare una intensità incidente (che è calcolabile come se ci fosse solo il campo incidente) e analogamente un’intensità riflessa; esse sono esprimibili mediante la formula introdotta nelle precedenti lezioni:
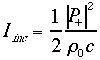 (13) e
(13) e 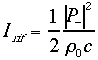 (14)
(14)
Facciamo ora una considerazione fisica: l’intensità di un’onda che giunge su una superficie viene in parte assorbita e in parte riflessa, quindi si scinde in due quote, come mostrato nello schema sottostante:
Schema 2
In formule, questo significa:
![]() (15)
(15)
A partire da questa espressione possiamo definire i concetti di coefficiente di riflessione e coefficiente di assorbimento; infatti se ora divido ambo i membri della (15) per ![]() ottengo dei rapporti che posso riformulare nel seguente modo:
ottengo dei rapporti che posso riformulare nel seguente modo:
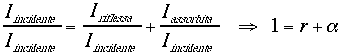 (16)
(16)
Dunque r è detto coefficiente di riflessione e![]() coefficiente di assorbimento.
coefficiente di assorbimento.
Ci è utile manipolare la (16) e sostituendo opportunamente la (13) e la (14) ricavare:
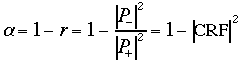 (17)
(17)
Questa è la grandezza che mi interessa misurare: nella pratica basta determinare il modulo della pressione riflessa e il modulo della pressione incidente all’interno del tubo e dal loro rapporto si risale al valore del coefficiente di assorbimento.
Il problema è che i moduli delle pressioni non si possono misurare direttamente, perchè fisicamente sono sempre sovrapposti e interagenti tra di loro.
C’è una teoria matematica complessa che permette di determinare l’andamento delle diverse grandezze all’interno del tubo; tuttavia esiste un metodo più semplice e più pratico per risalire ai valori di P+ e P- : supponiamo di introdurre nel tubo un microfono, libero di muoversi lungo l’asse del tubo stesso. Riportiamo in un diagramma il valore complessivo della pressione totale misurata dal microfono nei punti compresi tra —L e 0.
Risulterà un andamento simile a quello rappresentato nel grafico 1 (sottostante), nel quale è evidente la presenza di minimi e massimi (la pressione sulla parete raggiunge di solito un valore prossimo a quello massimo).
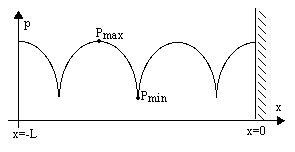
Grafico 1
I valori che mi interessano, che posso localizzare muovendo il microfono, sono proprio i massimi e i minimi, infatti essi si ottengono — come detto in precedenza — quando onda incidente e onda riflessa sono rispettivamente in fase o in controfase. Questa considerazione si traduce in termini analitici in un sistema lineare:
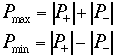 (18)
(18)
Avendo dunque misurato Pmax e Pmin , non è difficile ricavare i moduli di P+ e P-: basta risolvere il sistema, la cui soluzione è :
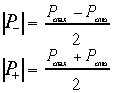 (19)
(19)
Raccogliendo Pmin nella (19) e sostituendo il tutto nella (17) ottengo l’espressione finale:
 (20)
(20)
Quindi immediatamente dopo aver misurato Pmax e Pmin , posso determinare il coefficiente di assorbimento.
Il diagramma che segue (Grafico 2) era usato come metodo grafico equivalente all’espressione (20) quando non esistevano le calcolatrici: rappresenta il coefficiente di assorbimento ![]() in funzione del rapporto
in funzione del rapporto ![]()
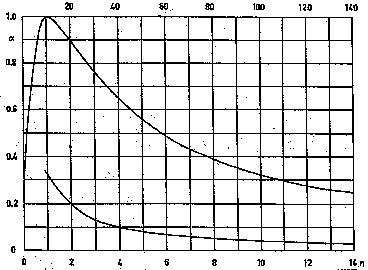
Grafico 2
La curva inferiore è la coda del grafico secondo la scala superiore (compressa di un fattore 10).
La soluzione raggiunta tramite l’equazione (20) è una soluzione semplificata, determinata in maniera empirica, ma corretta. Sarei potuto giungere allo stesso risultato tramite una soluzione completa dell’equazione d’onda, che mi avrebbe consentito di conoscere il valore della pressione non solo nel punto di massimo o di minimo, ma di descrivere analiticamente tutta la funzione di pressione. Qui di seguito si riporta il risultato della procedura matematica che è stata omessa:
![]() (21)
(21)
Inoltre, avendo trovato i moduli di P+ e P- posso direttamente ricavare il modulo dell’impedenza sulla pelle del materiale, tramite la formula (11).
Per conoscere analiticamente anche la fase dell’impedenza, è necessario far riferimento al termine ![]() dell’espressione (21). Tuttavia possiamo inquadrare meglio il significato fisico della fase con l’esempio che segue.
dell’espressione (21). Tuttavia possiamo inquadrare meglio il significato fisico della fase con l’esempio che segue.
Esempio: ipotizziamo che sulla pelle del materiale l’impedenza abbia un valore reale; per via della rotazione dei fasori ![]() e
e ![]() , anche se la riflessione sembra accadere senza sfasamento (perchè l’onda incidente è in fase con quella riflessa - ipotesi di impedenza reale), quando ci si sposta di un quarto d’onda (
, anche se la riflessione sembra accadere senza sfasamento (perchè l’onda incidente è in fase con quella riflessa - ipotesi di impedenza reale), quando ci si sposta di un quarto d’onda (![]() ) dal punto dove è avvenuta la riflessione, i due fasori sono ruotati ciascuno di 90°, ma in verso opposto e quindi si ritrovano sfasati di 180°. Questo significa che il primo minimo si verifica esattamente a distanza
) dal punto dove è avvenuta la riflessione, i due fasori sono ruotati ciascuno di 90°, ma in verso opposto e quindi si ritrovano sfasati di 180°. Questo significa che il primo minimo si verifica esattamente a distanza![]() dalla terminazione (si veda il grafico sottostante).
dalla terminazione (si veda il grafico sottostante).
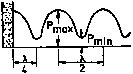
Grafico 3
Se invece il materiale che stiamo provando ha delle caratteristiche fisiche a causa delle quali dà luogo a un’impedenza complessa in x=0, il primo minimo si presenterà leggermente anticipato o posticipato rispetto alla distanza ![]() . Allora possiamo immaginare che un materiale dotato di impedenza complessa equivalga a un materiale con impedenza reale che però sia posizionato un po’ più avanti o un po’ più indietro rispetto al riferimento x=0. In altre parole, la fase dell’impedenza di un materiale non ha di per sè un grande significato fisico: è come dire che io vedo la superficie del materiale esattamente in x=0, ma che acusticamente esso reagisce più internamente; l’onda riflessa non si genera sulla pelle del materiale ma si genera ad una certa profondità nel materiale, tale che questa profondità disti comunque
. Allora possiamo immaginare che un materiale dotato di impedenza complessa equivalga a un materiale con impedenza reale che però sia posizionato un po’ più avanti o un po’ più indietro rispetto al riferimento x=0. In altre parole, la fase dell’impedenza di un materiale non ha di per sè un grande significato fisico: è come dire che io vedo la superficie del materiale esattamente in x=0, ma che acusticamente esso reagisce più internamente; l’onda riflessa non si genera sulla pelle del materiale ma si genera ad una certa profondità nel materiale, tale che questa profondità disti comunque ![]() dal primo minimo che ho identificato.
dal primo minimo che ho identificato.
Quindi, misurando la distanza del minimo dalla superficie, si può effettivamente risalire alla fase dell’impedenza; tuttavia comunemente è necessario determinare unicamente il modulo dell’impedenza.
Infine, possiamo verificare alcune considerazioni fatte in precedenza: il Grafico 4 che segue si riferisce a una terminazione rigida (![]() ), dove il valore minimo della pressione è prossimo allo zero.
), dove il valore minimo della pressione è prossimo allo zero.
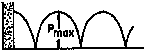
Grafico 4
Nel caso precedente (Grafico 3), invece, la terminazione non è rigida e l’interferenza tra onda riflessa e incidente dà luogo a valori finiti e confrontabili di Pmax e Pmin .
Un prototipo di tubo ad onde stazionarie
Occupiamoci di alcuni particolari costruttivi del tubo ad onde stazionarie, detto anche tubo di Kundt; nella figura sottostante è rappresentata la versione commercializzata dalla ditta Brüel&Kjær di Copenaghen:

Figura 1
Si possono adoperare due tubi permutabili: uno dal diametro di circa 100mm e lungo circa 1,5m e un altro (che si vede montato sopra l’altoparlante) che ha un diametro di 29mm ed è lungo circa 0,5m. All’estremità si collocano i portaprovini (gli anelli di acciaio che si intravedono in alto a destra), all’interno dei quali si alloca il materiale da provare (intonaco, gommapiuma).
Il tubo viene quindi montato sullo scatolotto di legno di forma rettangolare (che contiene un altoparlante) e il microfono è quel cilindro orizzontale che si muove su un carrellino (visibile in Figura 1) e prende il segnale attraverso un tubicino (il "microphone probe" indicato nel sottostante Schema 3) che scorre dentro al tubo centrale e fa da trasduttore di pressione lungo l’asse. Sulla base del supporto per il microfono c’è una stecca graduata con un cursore che consente di misurare con la precisione di 1/10mm le distanze dal provino.
Segue uno schema di principio del tubo di Kundt:
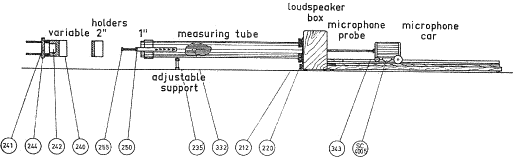
Schema 3
Nello schema funzionale che segue (Schema 4) è rappresentato il classico uso del tubo: per compiere le misure è necessario un generatore di segnale sinusoidale da applicare all’altoparlante e i valori del rapporto ![]() si misurano grazie alla lettura sul voltmetro dei valori di tensione (in
si misurano grazie alla lettura sul voltmetro dei valori di tensione (in![]() , su una scala di precisione) provenienti dal microfono e si può così desumere il coefficiente di assorbimento grazie al Grafico 2 (già riportato a pag.7).
, su una scala di precisione) provenienti dal microfono e si può così desumere il coefficiente di assorbimento grazie al Grafico 2 (già riportato a pag.7).
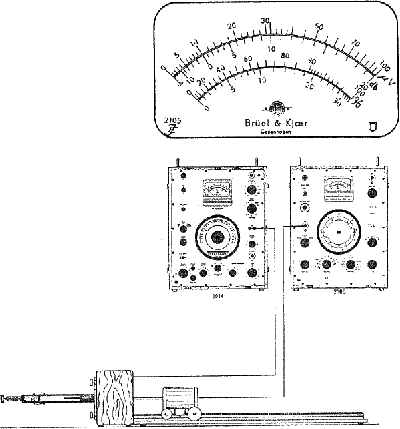
Schema 4
Il tubo di Kundt è uno strumento ormai caduto in disuso, per una serie di motivi:
Esistono tecniche più moderne che si basano su misure in banda larga: anzichè generare un suono puro a una singola frequenza, si produce un segnale che copre una vasta zona dello spettro di frequenze; utilizzando teorie complesse di analisi dei segnali, si ricava direttamente lo spettro di assorbimento. Recentemente sono state sviluppate ulteriori tecniche di misura basate sull’intensimetria, che non richiedono l’ipotesi di onde piane e che quindi si possono compiere anche al di fuori del tubo. Il tubo ad onde stazionarie rimane tuttavia un utile modello didattico.
Densità di energia sonora
Sappiamo che il prodotto ![]() rappresenta un trasporto di energia nel mezzo acustico.
rappresenta un trasporto di energia nel mezzo acustico.
Definiamo ora la densità di energia, cioè la quantità di energia per metro cubo:
![]() (22)
(22)
la seconda definizione è più precisa, appunto perchè esprime un valore locale di densità.
Consideriamo ora il caso particolarmente semplice di un’onda piana progressiva che entra attraverso una superficie di sezione 1 m2 (Schema 5): se si immagina di lasciar fluire l’onda attraverso questa superficie per un secondo essa invaderà un volume di forma prismatica e di valore ![]() , dove c è chiaramente la velocità del suono.
, dove c è chiaramente la velocità del suono.
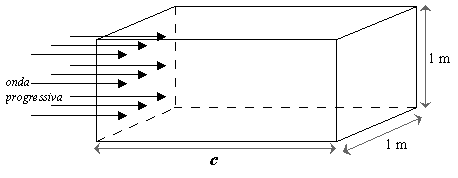
Schema 5
L’energia entrata in questo prisma si può scrivere come: ![]() , dove S è la sezione del prisma, in questo caso unitaria; quindi si ricava la relazione fondamentale della densità di energia:
, dove S è la sezione del prisma, in questo caso unitaria; quindi si ricava la relazione fondamentale della densità di energia:
![]() (23)
(23)
Ricordiamo a questo punto le espressioni delle intensità che si ricavano a partire dai valori medi quadratici della pressione e della velocità (dalle precedenti lezioni):
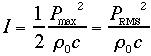 e
e ![]()
In conseguenza di ciò si è portati a pensare che si possa esprimere la densità di energia sonora per un’onda piana progressiva in due modi equivalenti (derivati dalle ultime due equazioni), quali:
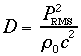 (24) oppure
(24) oppure ![]() (25)
(25)
Analiticamente la derivazione di quest’ultime equazioni è corretta, ma fisicamente esse sono un modello sbagliato di ciò che sta succedendo: secondo la (24) la densità di energia è rappresentata da sola energia potenziale e viceversa secondo la (25) è presente solo energia cinetica. Invece, all’interno di quel volume, in certi punti l’energia sarà cinetica e in certi punti sarà potenziale: l’energia totale contenuta nel volume è corretta, ma la sua esplicazione analitica è sbagliata.
La considerazione fisica ragionevole è questa: mediamente nel tempo e nello spazio l’energia sarà metà cinetica e metà potenziale, perchè oscilla tra l’una e l’altra condizione. Quindi il procedimento corretto è combinare le ultime due espressioni nella nuova:
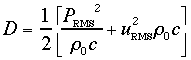 (26)
(26)
Questa formula è vera sempre, cioè non dipende dal tipo di campo sonoro che si sta considerando: questo è dovuto alla suo forte significato fisico, che si manifesta dall’unione delle due espressioni precedenti. Essa rappresenta correttamente il fenomeno fisico anche in casi diversi da quello dell’onda piana progressiva.
Un altro modo per calcolare il coefficiente di assorbimento
Applichiamo i risultati ottenuti per la densità di energia nel caso delle delle onde stazionarie: lo scopo è determinare il coefficiente di assorbimento di un materiale escogitando e sfruttando un nuovo metodo.
Riprendendo la formula (16) secondo la quale:
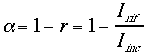
ci proponiamo di determinare Iinc e Irif sfruttando la densità di energia.
Innanzitutto possiamo affermare che è sempre valida l’ipotesi di sovrapponibilità degli effetti per cui possiamo distinguere l’intensità totale nella componente riflessa e in quella incidente:
![]() (27)
(27)
Possiamo evidenziare graficamente la situazione (Schema 6):
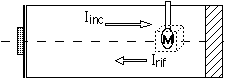
Schema 6
Nel volumetto d’aria che contorna il microfono si manifestano le due componenti del campo sonoro; tuttavia un semplice microfono non è più utile: ci interessa misurare l’intensità totale del campo sonoro e per questo necessitiamo di un dispositivo che misuri simultaneamente il valore di P e di u e ne faccia il prodotto mediato, infatti: ![]() .
.
Nella (2) compare un segno meno, perchè l’intensità è un vettore e, come già detto riguardo alla velocità nella (8), l’intensità incidente e quella riflessa hanno verso opposto.
Presa singolarmente, ciascuna di queste componenti rappresenta l’intensità di un’onda piana progressiva, quindi per ciascuna vale l’espressione (23) della densità. Allora, avvalendoci nuovamente dell’ipotesi di sovrapponibilità degli effetti, possiamo esprimere la densità di energia totale nel tubo:
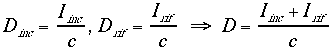 (28)
(28)
Siccome la densità è uno scalare, il contributo dell’onda incidente e il contributo dell’onda riflessa sono stati direttamente sommati.
Adesso, combinando la (28) con la (23) posso scrivere un sistema lineare:
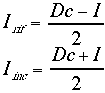 (29)
(29)
Ricordiamo che, una volta misurati P ed u, il valore di I è immediatamente calcolato e D è noto tramite la (26), quindi Iinc e Irif sono determinati.
Inoltre, siccome per definizione![]() , è immediato ricavare:
, è immediato ricavare:
![]() (30)
(30)
che era l’espressione che ci interessava.
Questo procedimento introduce svariati vantaggi:
Il metodo appena illustrato per la determinazione del coefficiente di assorbimento ![]() è il più moderno ed elegante di cui si disponga: richiede una strumentazione più sofisticata (prima bastavano un microfono e un voltmetro), come il dispositivo a due canali di misura già citato poco sopra, ma permette di determinare rapidamente il coefficiente con un’unica misura, valida per tutte le frequenze.
è il più moderno ed elegante di cui si disponga: richiede una strumentazione più sofisticata (prima bastavano un microfono e un voltmetro), come il dispositivo a due canali di misura già citato poco sopra, ma permette di determinare rapidamente il coefficiente con un’unica misura, valida per tutte le frequenze.