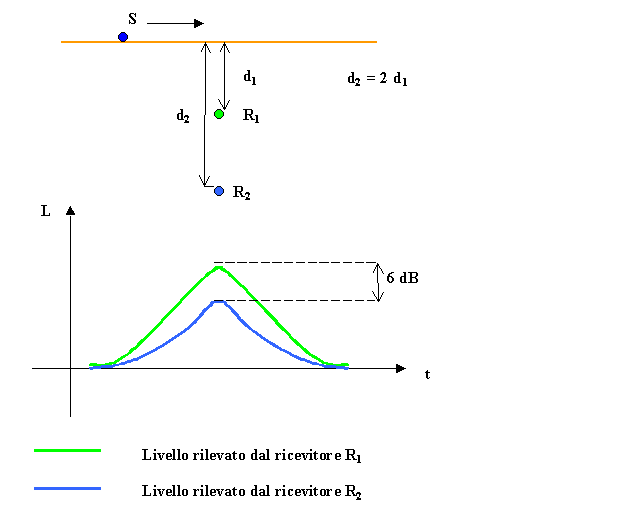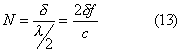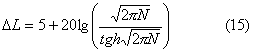PROPAGAZIONE ESTERNA

INDICE

1. PROPAG. EST. CON SORGENTE PUNTIFORME - PAG. 2

2. PROPAG. EST. CON SORGENTE LINEARE - PAG. 7

3. PROFILO DI TEMPERATURA - PAG. 10

4. RIFLESSIONE SU UNA SUPERFICIE PIANA - PAG. 12

5. DIFFRAZIONE - PAG. 14

1. PROPAGAZIONE ESTERNA CON SORGENTE PUNTIFORME

Consideriamo la propagazione del suono in campo libero, cioè in ambienti aperti, senza che vi siano fenomeni di riflessione o ostacoli che condizionino la propagazione stessa.

Supponiamo di avere ad esempio un'onda sferica, prodotta da una sorgente sferica pulsante o da una sorgente di dimensioni trascurabili rispetto alla lunghezza d'onda; supponiamo quindi di porre un ricevitore ad una distanza tale da trovarci fuori dal cosiddetto "campo vicino", in cui la pressione e la velocità sono fuori fase. Nel punto dove poniamo il ricevitore vogliamo invece che queste due grandezze siano in fase e decadano linearmente con la distanza.

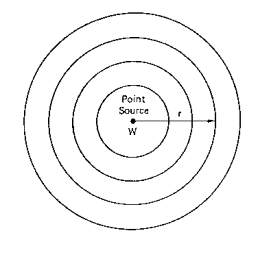
Fig. 1 - Sorgente puntiforme

Se la sorgente ha una potenza W, a distanza r l'intensità è:

.

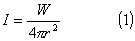Supponiamo ad esempio che a distanza r₁ = 1 m il livello di intensità sia:

;

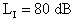a distanza r₂ = 2 m si ha:

.

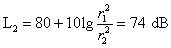In poche parole in campo libero, in presenza di una sorgente sferica, con il raddoppiare della distanza il livello di intensità diminuisce di 6 dB.

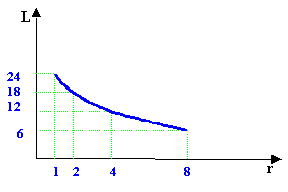
Fig. 2 - Variazione del livello con la distanza con una sorgente puntiforme

Chiamiamo tale diminuzione nel seguente modo:

.

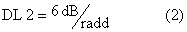Questa è la massima attenuazione possibile, considerando la propagazione in campo libero e quindi l'aria come mezzo non dissipativo. Non avvenendo dissipazione, quindi, l'intensità cala solo perché aumentando la distanza il fronte d´onda diventa piú vasto e l´energia deve distribuirsi su una superficie maggiore.

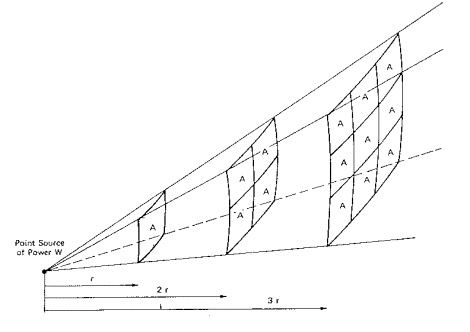
Fig. 3 - Propagazione del suono da una sorgente puntiforme

Il livello di intensità è espresso dalla formula:

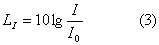
I₀ : intensità di riferimento = 1× 10^-12 W / m²

In maniera del tutto analoga i livelli di potenza, densità, pressione e velocità sono espressi rispettivamente da:

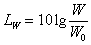
W₀ : potenza di riferimento = 1× 10^-12 W

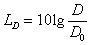
D₀ : densità di riferimento

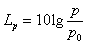
p₀ : pressione di riferimento

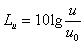
u₀ : velocità di riferimento (4)

Sostituendo la (1) nella (3), moltiplicando e dividendo per W₀, si ha:

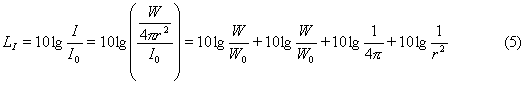
Semplificando le opportune quantità si ottiene la cosiddetta :

FORMULA DEL CAMPO LIBERO: L_I = L_W - 11 - 20 lg r (6)

Inoltre, lavorando sui valori di riferimento, è possibile far sì che i livelli di intensità, pressione, velocità e densità di energia assumano lo stesso valore in condizioni di massima propagazione, cioè con Z = r₀ × c , e quindi nelle situazioni in cui vi sia una sogente piana o una sorgente sferica ma ponendosi a grandi distanze da essa. Tali valori sono:

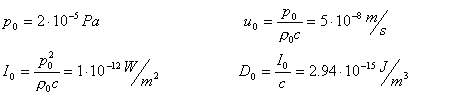
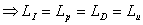
In condizioni diverse da queste così favorevoli si può dire invece che:

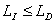
Pertanto le condizioni di propagazione possono essere valutate mediante la quantità:

Non ha invece senso definire la quantità: L_P - L_I perché se l'intensità è legata direttamente all'energia, la pressione (come anche la velocità) al quadrato è legata all'energia solo in prima approssimazione. Le norme ISO9614 prevedono invece di qualificare la natura del campo sonoro proprio con tale quantità, e quindi erroneamente. Basti pensare ad esempio al tubo ad onde piane e stazionarie:

Fig. 4 - Tubo a onde piane e stazionarie con andamento del livello di pressione e di intensità

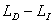
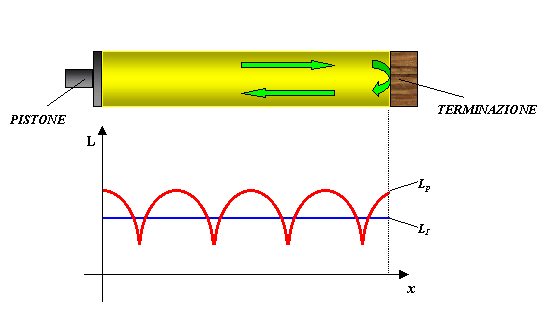
Si nota facilmente che all'interno del tubo la quantità L_P - L_I cambia, diventando a seconda della posizione positiva, nulla o negativa.

2. PROPAGAZIONE ESTERNA CON SORGENTE LINEARE

Un altro caso da poter considerare è quello di una sorgente lineare, costituita cioè da una serie di sorgenti puntiformi in fila.

Una sorgente lineare può essere ad esempio un'automobile in movimento su una strada. In questa situazione si genera un'onda caratterizzata da un fronte cilindrico e si può solo calcolare il livello equivalente, visto che la sorgente modifica nel tempo la sua posizione rispetto al ricevitore e il livello rilevato varia nel tempo.

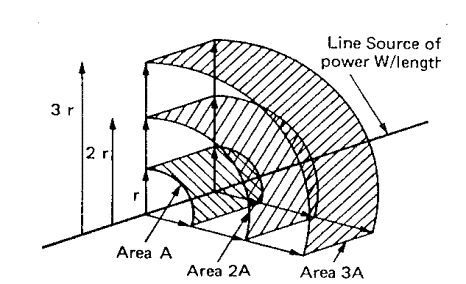
Fig. 5 - Propagazione del suono da una sorgente lineare

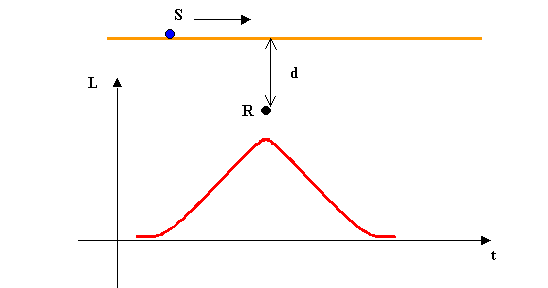
Fig. 6 - Andamento del livello nel tempo con una sorgente in movimento rispetto al ricevitore (sorgente lineare)

Se la sorgente ha una potenza W, a distanza r l'intensità è:

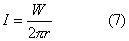
Se consideriamo un altro ricevitore posto a distanza doppia del primo notiamo che la differenza di livello equivalente è pari a 3dB.

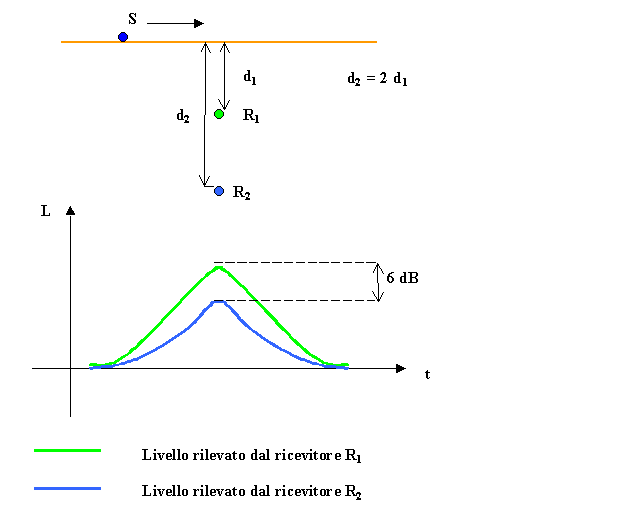
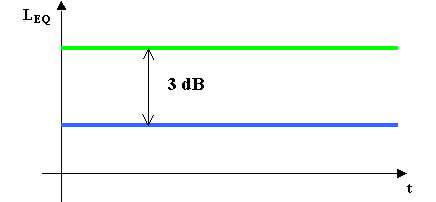
Fig. 7 - Andamento del livello equivalente nel tempo con una sorgente in movimento rispetto a due ricevitori posti a distanza doppia

Quindi in presenza di una sorgente lineare, con il raddoppiare della distanza il livello di intensità (equivalente) diminuisce di 3 dB.

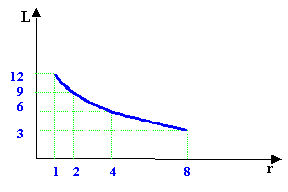
Fig. 8 - Variazione del livello con la distanza con una sorgente lineare

3. PROFILO DI TEMPERATURA

Normalmente la temperatura dell'aria tende ad abbassarsi con l'aumentare della quota; tuttavia in alcuni casi avviene il fenomeno dell'inversione termica: fino ad una certa quota la temperatura aumenta e, superata tale quota, comincia a decrescere. Un'altra situazione è caratterizzata da normale crescita di temperatura fino a una certa quota, quindi, ad una certa altezza, c'è inversione termica e successivamente la temperatura ricomincia a crescere.

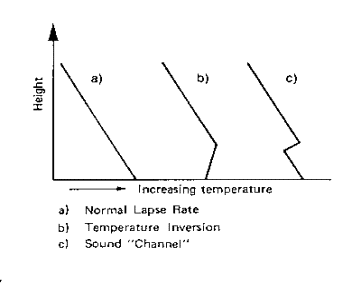
Fig. 9 - Profilo di temperatura

L'andamento delle linee di suono è rappresentato in figura 10:

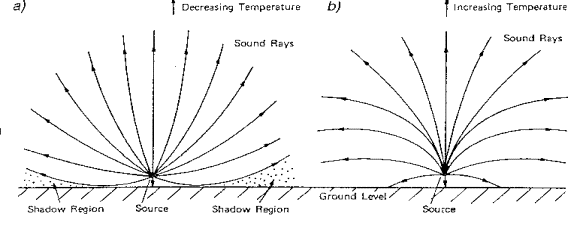
Fig. 10 - Andamento delle linee di suono in funzione della temperatura

Caso a

La curvatura dei raggi tende verso le temperature fredde; possono esserci dei raggi tangenti alla superficie con conseguente creazione di zone d'ombra.

Caso b

La curvatura dei raggi è opposta a quella del caso a, non si creano zone d'ombra e il suono può oltrepassare eventuali ostacoli.

Caso c

I raggi si possono propagare anche orizzontalmente e il suono può essere trasportato per lunghe distanze con scarsa attenuazione.

4. RIFLESSIONE SU UNA SUPERFICIE PIANA

Se i raggi provenienti da una sorgente incidono su una superficie piana si formano dei raggi riflessi che sembrano provenire da una sorgente immagine, posta al di là della superficie, in posizione simmetrica rispetto a quella della sorgente reale. Questi raggi riflessi si sommano a quelli provenienti dalla sorgente reale, provocando diversi fenomeni a seconda della natura del suono.

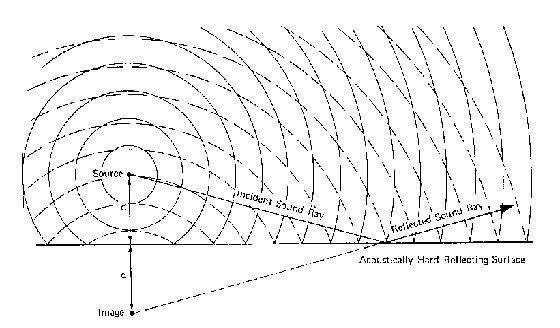
Fig. 11 - Riflessione su una superficie piana

Suono periodico e stazionario

In questo caso entrambe le sorgenti emettono lo stesso suono, che percorrendo cammini di diversa lunghezza, genera il fenomeno dell'interferenza.

Nei punti in cui i due segnali arrivano in fase (nel diagramma sono i punti nei quali si ha l'incrocio delle linee) si ha un incremento di 6 dB per raddoppio di distanza. L'incremento sarà in realtà minore perché il suono riflesso ha energia più bassa di quello diretto.

Nel centro delle figure delimitate dagli incroci delle circonferenze il suono arriva sfasato di 180° e si ha un cancellazione sonora. Anche qui, poiché il suono riflesso è minore del suono diretto, la cancellazione sarà solo parziale.

Suono variabile

Il suono emesso dalla sorgente riflessa, dovendo percorrere un distanza maggiore, sarà assolutamente diverso e non correlato rispetto a quello della sorgente diretta; si sommano quindi le intensità.

L'incremento massimo sarà sempre minore o uguale a 3 dB ogni raddoppio di distanza.

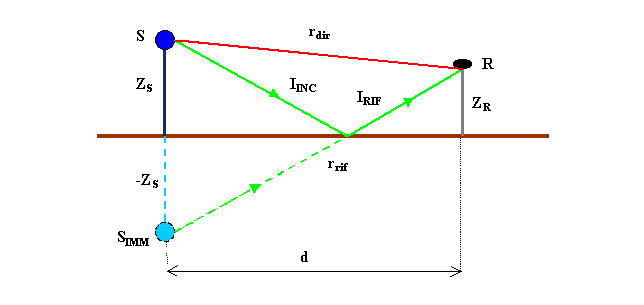
Fig. 12 - Il ricevitore R rileva il suono riflesso dalla superficie piana

In figura 12 è rappresentato un ricevitore R che rileva il suono riflesso da una superficie piana. Esso è posto a distanza d da una sorgente S di potenza W e indichiamo con r_dir e r_rif rispettivamente i cammini dei raggi diretto e riflesso; t esprime invece il tempo impiegato dal raggio per percorrere il cammino sorgente-ricevitore. Ricordando che c è la velocità di propagazione del suono si può quindi scrivere:

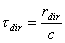
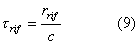
Se il suono è un impulso vale: t_rif > t_dir

Le formule (9) valgono in condizioni di totale riflessione; diversamente, se c'è un assorbimento dato dal coefficiente a, si ha:

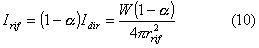
5. DIFFRAZIONE

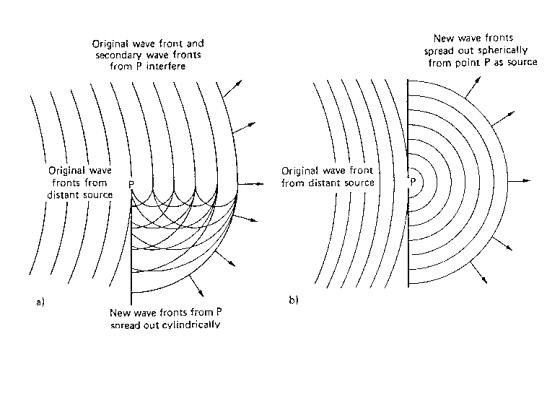Fig. 13 - Diffrazione di uno schermo (a) e di un buco (b) a bassa frequenza

La figura 13 mostra quello che avviene alle basse frequenze attraverso un muro di cinta (figura 13.a) e attraverso un buco in una parete (figura 13.b). Il buco o lo schermo diffrangono le onde che arrivano, formando dei fronti d'onda curvi, che sembrano essere prodotti dal bordo di difrazione. Questo fenomeno è legato alla natura ondosa della propagazione acustica e fa sì che non si crei un'onda vera propria dietro allo schermo.

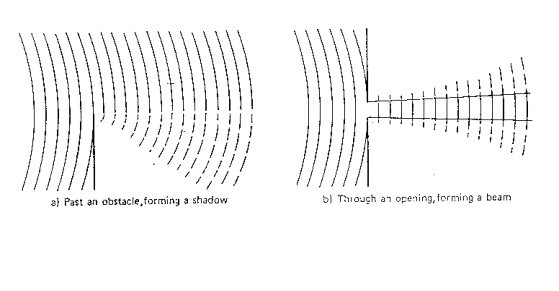Fig. 14 - Effetto di uno schermo (a) e di un buco (b) sulla propagazione del suono alle alte frequenze

Alle alte frequenze si può notare un miglioramento come da figura 14. C'è infatti una parziale ricomposizione dell'onda nella zona successiva allo schermo.

In generale è però difficile da quantificare.

C'è un caso molto semplice nel quale è stata trovata una soluzione analitica semplificata: è la formulazione di MAEKAWA, che vale nel caso di schermi sottili di lunghezza indefinita e sorgenti puntiformi.

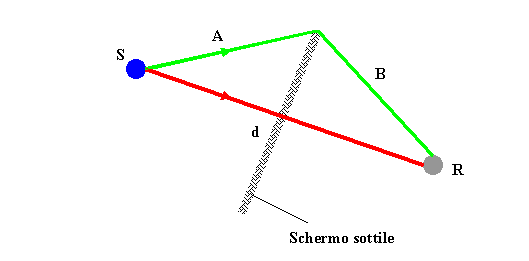
Fig. 15 - Differenza di cammino causata dalla presenza di uno schermo sottile

In figura 15 sono rappresentati i cammini che il suono percorrerebbe nel caso in cui ci fosse lo schermo (tratto verde) e nel caso in cui lo stesso non ci fosse (tratto rosso).

Si ha quindi una differenza di cammino: d = A + B - d (11)

E di livello pari a: DL = L_DIRETTO - L_DIFFRATTO (12)

Tale variazione di livello è proporzionale al numero di Fresnel:

Vale in questo caso la:

RELAZIONE DI MAEKAWA:

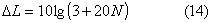
Un'altra relazione è quella di Kurz, più accurata in presenza di piccoli valori di N:

RELAZIONE DI KURZ:

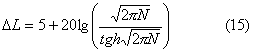
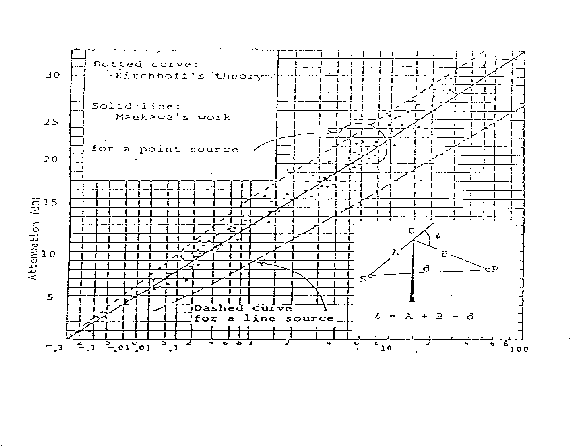Fig. 16 - Diagramma di Maekawa
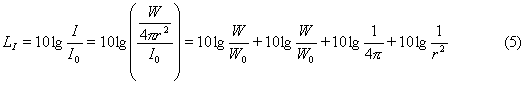
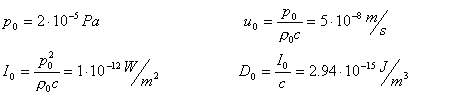