Questo documento include i seguenti argomenti:
Lo scambio termico per irraggiamento avviene tramite l'emissione o la ricezione di onde elettromagnetiche da parte di più corpi. Ogni corpo ad una certa temperatura T emette e riceve radiazioni elettromagnetiche con una certa intensità che può essere variabile nel tempo, indipendentemente dal mezzo in cui si trova, quindi anche nel vuoto.

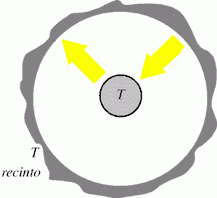
Se si pone un recinto attorno al corpo alla sua stessa temperatura, la temperatura del corpo non varia. Infatti, congruamente al Primo Principio della Termodinamica, i corpi si scambiano calore a seconda della differenza di temperatura a cui si trovano, e ciò si verifica anche per l'irraggiamento: è sufficiente che i corpi si vedano, e se sono alla stessa temperatura, lo scambio di onde elettromagnetiche è in condizioni di equilibrio. Si può così verificare concettualmente che i corpi che possono scambiarsi calore solo per irraggiamento vanno in equilibrio termico quando tante radiazioni emettono quante ne ricevono.
Affinché si verifichi il fenomeno di irraggiamento di energia,
è necessario che sia il campo elettrico che il campo magnetico fluttuino
nel tempo. Se non c'è oscillazione infatti non c'è radiazione:
è di esperienza comune la presenza di forti campi statici di tipo magnetico
nelle calamite o di tipo elettrico nei condensatori che non irradiano calore.
L'irraggiamento di onde elettromagnetiche si può schematizzare graficamente
come due vettori ortogonali a se stessi ed alla direzione di propagazione, denominati
campo elettrico E e campo magnetico B, che oscillano nel tempo
sul proprio asse.
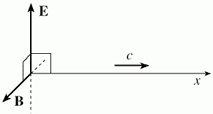
Fig. 1 - Propagazione nello spazio
La propagazione nel vuoto di un'onda di questo tipo avviene alla velocità della luce:
c=300000 km/s (1)
Nei mezzi invece avviene alla velocità della luce corretta con un opportuno indice di rifrazione (che nel vuoto è uguale a uno):
![]() (2)
(2)
Oltretutto solo il vuoto è completamente trasparente alla
radiazione elettromagnetica: nei mezzi si considera sempre un coefficiente
di estinzione ![]() che influisce esponenzialmente sull'intensità della radiazione nel seguente
modo:
che influisce esponenzialmente sull'intensità della radiazione nel seguente
modo:
![]() (3)
(3)
Se osservo i vettori E e B al variare del tempo, noto che fluttuano con una certa periodicità, schematizzabile graficamente con un sinusoide di lunghezza d'onda:
![]() (4)
(4)
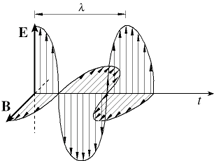
Fig. 2 - Propagazione nel tempo
Se campo elettrico e campo magnetico si trovano in fase (come
in figura) si ha la massimizzazione del trasporto di energia. Si possono notare
molte analogie in questo senso con la propagazione di onde acustica. Anche nelle
onde acustiche si ha a che fare con due grandezze variabili, con la differenza
che, nel caso di onde elettromagnetiche, sono entrambe vettoriali e sono ortogonali
alla direzione di propagazione.
Differentemente all'acustica, nell'irraggiamento è rarissima l'emissione
in tono puro con oscillazione sinusoidale (qui chiamata monocromatica): l'unico
caso di questo tipo è il laser, mentre i corpi tendono ad emettere rumore
in banda larga. Solo certi corpi, detti colorati, hanno emissione privilegiata
a certe lunghezze d'onda, oppure altri corpi, detti grigi, hanno emissione uniforme
su tutto lo spettro.
Nel campo delle onde elettromagnetiche è di uso convenzionale realizzare
il grafico dello spettro in funzione delle lunghezze d'onda anziché della
frequenza. Questa scelta ne ribalta l'interpretazione rispetto all'acustica:
le basse frequenze si trovano sul lato destro dello spettro e le alte sul lato
sinistro.
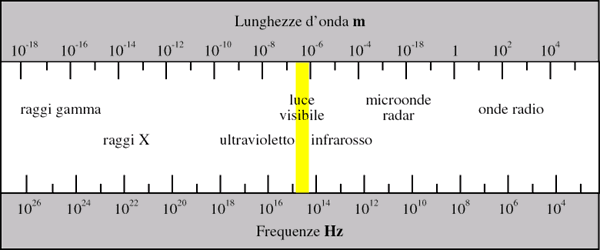
Fig. 3 - Spettro onde elettromagnetiche
Da un punto di vista energetico, nessun tipo di radiazioni elettromagnetiche
è trascurabile: si possono sperimentare i loro effetti termici a diverse
lunghezze d'onda esponendosi al sole, utilizzando i telefoni cellulari o i forni
a microonde, e così via. Quindi termicamente tutto lo spettro è
da considerare, ed il trasferimento di energia si ha a qualunque lunghezza d'onda.
L'effetto di trasferimento di energia dalla radiazione al mezzo attraversato,
dipende quindi da b coefficiente di estinzione che regola la quota di energia
"intrappolata" durante l'attraversamento. I corpi opachi, ad esempio,
hanno coefficiente ![]() altissimo, che può essere reso finito solo se ne consideriamo strati
di spessore micrometrico (come quelli ricavati dall'affettatrice micrometrica
per microscopi), facendo così diventare il materiale trasparente.
altissimo, che può essere reso finito solo se ne consideriamo strati
di spessore micrometrico (come quelli ricavati dall'affettatrice micrometrica
per microscopi), facendo così diventare il materiale trasparente.
Nel campo del visibile inoltre si valuta abitualmente la radiazione in base
al suo colore. Ma non è detto che il colore percepito sia figlio di una
radiazione monocromatica pura. Il sistema percettivo umano estrae il tono dall'insieme
dello spettro, rendendo la valutazione fisica di questo parametro abbastanza
complessa.
Da tutte queste considerazioni nasce la necessità di definire
delle grandezze che consentano di stabilire la quota di energia scambiata dai
corpi per irraggiamento.
Si definisce così il potere emissivo integrale ![]() o densità di flusso termico, quantità dipendente solo dalla temperatura,
quindi sempre positiva, che ha la grandezza di
o densità di flusso termico, quantità dipendente solo dalla temperatura,
quindi sempre positiva, che ha la grandezza di ![]() ,
e che fa riferimento all'energia totale di tutto lo spettro.
,
e che fa riferimento all'energia totale di tutto lo spettro.
Altra grandezza utile per l'irraggiamento è il potere emissivo specifico
o monocromatico, definito come:
![]() (5)
(5)
che viene calcolato in uno specifico punto dello spettro. È quindi facile ricavare che:
![]() (6)
(6)
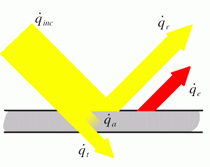
Si può notare che un corpo opaco, oltre ad irradiare una
certa ![]() , riflette
una quantità
, riflette
una quantità ![]() di radiazione ricevuta
di radiazione ricevuta ![]() ,
dopo averne assorbita una quantità
,
dopo averne assorbita una quantità ![]() ed eventualmente trasmessa una quantità
ed eventualmente trasmessa una quantità ![]() .
.
La ![]() irradiata è molto piccola, o addirittura al di fuori del campo visibile
stesso. È per questo che i colori dei corpi a temperatura ambiente, per
come percepiti dall'occhio umano, dipendono soprattutto dalla
irradiata è molto piccola, o addirittura al di fuori del campo visibile
stesso. È per questo che i colori dei corpi a temperatura ambiente, per
come percepiti dall'occhio umano, dipendono soprattutto dalla ![]() riflessa. Solo alle alte temperature la
riflessa. Solo alle alte temperature la ![]() irradiata inizia a diventare rilevante ed i corpi si colorano a partire dal
rosso.
irradiata inizia a diventare rilevante ed i corpi si colorano a partire dal
rosso.
Partendo dalla semplice relazione:
![]() (7)
(7)
dividendo membro a membro per ![]() :
:
![]() (8)
(8)
e definendo:
![]()
![]()
![]() (9)
(9)
rispettivamente come coefficienti di assorbimento, di riflessione
e di trasmissione, si ha che, trascurando quest'ultimo, e ricavando ![]() :
:
![]() (10)
(10)
Il coefficiente di assorbimento a ha un suo spettro che varia tra 0 e 1 in funzione della temperatura.
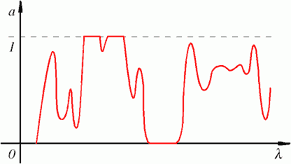
Fig. 4 - Ipotetico spettro di a
Grazie al coefficiente di assorbimento si può ora definire
con precisione l'assorbitore totale o corpo nero, come corpo che
ha a=1 relativamente ad ogni lunghezza d'onda. Un oggetto di questo genere
assorbe la radiazione di qualunque ![]() senza rifletterla, nonostante sia un grande emettitore ed alle alte temperature
possa colorarsi per emissione.
senza rifletterla, nonostante sia un grande emettitore ed alle alte temperature
possa colorarsi per emissione.
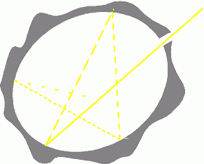
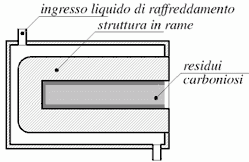
Fig. 5 - Realizzazione teorica e pratica di un corpo nero.
I raggi che entrano nel corpo nero si estinguono prima di riuscire ad uscire.
Il corpo grigio invece è un corpo che ha il coefficiente
a<1, ma costante a tutte le lunghezze d'onda. Infine il corpo bianco
ha a=0 per tutte le frequenze e quindi assorbimento nullo.
Il coefficiente a non è però sufficiente a definire il colore
percepito di un oggetto. Il colore infatti dipende per la maggior parte dalla
luce incidente. Una corretta colorimetria può quindi essere realizzata
solo determinando la funzione di trasferimento fra lo spettro della luce incidente
e quello della luce riflessa.
Ai fini dello scambio termico è interessante solamente la radiazione
emessa, mentre la radiazione riflessa è fonte di disturbo soprattutto
per gli strumenti di misura.
La legge di Stefan - Boltzmann ci fornisce il valore numerico del potere emissivo integrale per un corpo nero:
![]() (11)
(11)
dove ![]() è detta costante di Stefan - Boltzmann e vale:
è detta costante di Stefan - Boltzmann e vale:
![]() (12)
(12)
Riportando su di un grafico i valori di ![]() in funzione della temperatura si ottiene un ramo di parabola.
in funzione della temperatura si ottiene un ramo di parabola.
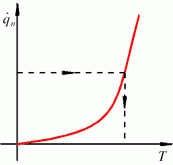
È immediato notare la complessità strumentale che
può nascere dalla misura di ![]() ,
dovuta alle notevoli differenze di precisione necessarie per valutare la temperatura
risultante: per bassi valori del potere emissivo integrale è utile un'alta
precisione per ottenere un corretto valore di T nell'ampio campo di valori
possibili. Nel caso di alti valori di
,
dovuta alle notevoli differenze di precisione necessarie per valutare la temperatura
risultante: per bassi valori del potere emissivo integrale è utile un'alta
precisione per ottenere un corretto valore di T nell'ampio campo di valori
possibili. Nel caso di alti valori di ![]() invece vi è la situazione complementare.
invece vi è la situazione complementare.
Sempre da questo grafico è possibile notare come il corpo nero abbia
un'altissima emissione di radiazioni alle alte temperature.
È utile infine
ricordare che l'energia emessa si modifica al variare della temperatura del
corpo stesso, ma la quota ricevuta invece non varia, se non con dipendenza dalla
temperatura del corpo emittente.
La legge di Prevost definisce in maniera semplice l'energia che viene scambiata per irraggiamento:
![]() (13)
(13)
Grazie alla legge di Prevost e ad un semplice esperimento è
possibile ricavare alcune relazioni sul corpo grigio: ponendo un corpo grigio
in un recinto realizzato con un corpo nero, entrambi alla stessa temperatura,
è immediato per Prevost verificare che ![]() è nullo (visto che il flusso emesso e il flusso ricevuto dal corpo sono
uguali).
è nullo (visto che il flusso emesso e il flusso ricevuto dal corpo sono
uguali).
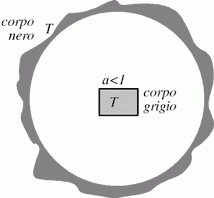
Essendo però il corpo centrale grigio, non catturerà tutta l'energia irradiata dal corpo nero, ma solo una parte dipendentemente dal suo coefficiente a:
![]() (14)
(14)
che sarà pure uguale a quella irradiata a qualunque temperatura. Si arriva quindi all'importante conclusione che:
![]() (15)
(15)
dove e è il coefficiente di emissione. Per un corpo grigio quindi è sufficiente porre il coefficiente a davanti alla formula di Stefan - Boltzmann per ottenere il potere emissivo integrale. Se invece il corpo non è grigio la situazione si complica, ma sperimentalmente si ottiene sempre che l'emissione bilancia l'assorbimento:
![]() (16)
(16)
Per i nostri scopi sarà però sufficiente studiare solamente il corpo grigio.
La legge di Planck fornisce lo spettro di emissione del corpo nero:
![]() (17)
(17)
dove:
![]() (18)
(18)
![]() (19)
(19)
sono le costanti di Planck.
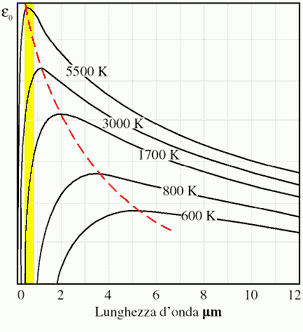
Fig. 6 - Spettro di emissione del corpo nero. La banda gialla indica il campo del visibile.
Tracciando il grafico del potere emissivo specifico ottenuto dalla
legge di Planck per diverse temperature costanti, si ottengono delle curve che
hanno il loro massimo in corrispondenza del colore di emissione privilegiato.
Si nota subito come questo massimo si sposti verso le basse frequenze al diminuire
di T.
È grazie allo spettro di emissione del corpo nero che si
è riusciti a dare una definizione precisa di temperatura di colore,
come la temperatura della curva che minimizza gli scarti nei confronti dello
spettro reale di una fonte luminosa.
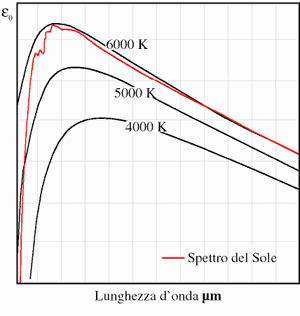
Fig. 7 - Spettro di emissione del Sole a confronto con quello
del corpo nero.
È possibile notare come la temperatura della luce solare si avvicini
ai 6000K.
Detta anche legge del regresso, indica il punto di massimo
dello spettro della legge di Planck. Derivando infatti quest'ultima rispetto
a ![]() ed imponendo che la derivata si annulli si ottiene che:
ed imponendo che la derivata si annulli si ottiene che:
![]() (20)
(20)
che rappresenta il luogo dei massimi dello spettro di emissione del corpo nero, ed è un ramo di iperbole.
È importante a questo punto analizzare come avviene l'emissione nello spazio e per far questo si definirà una nuova grandezza, il potere emissivo angolare, come:
![]() (21)
(21)
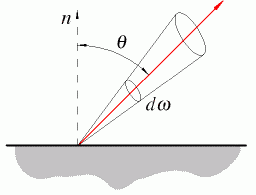
che ha la grandezza di ![]() e permette di ricavare immediatamente:
e permette di ricavare immediatamente:
![]() (22)
(22)
Cercando di analizzare la distribuzione spaziale di ![]() ,
l'ipotesi più ovvia è quella di porre il potere emissivo angolare
costante, che fornisce un solido di radiazione semisferico. Nella realtà
questa ipotesi è mal verificata, in quanto si ha sperimentalmente che
l'emissione è massima ortogonalmente alla superficie.
,
l'ipotesi più ovvia è quella di porre il potere emissivo angolare
costante, che fornisce un solido di radiazione semisferico. Nella realtà
questa ipotesi è mal verificata, in quanto si ha sperimentalmente che
l'emissione è massima ortogonalmente alla superficie.
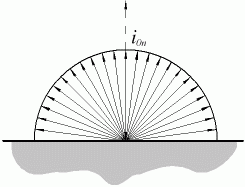
La legge di Lambert pone rimedio a questa incongruenza, definendo:
![]() (23)
(23)
dove ![]() rappresenta il potere emissivo lungo la direzione normale alla superficie, ottenendo
un solido di radiazione di tipo sferico.
rappresenta il potere emissivo lungo la direzione normale alla superficie, ottenendo
un solido di radiazione di tipo sferico.
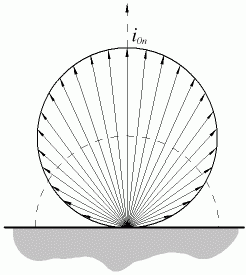
Purtroppo non è possibile applicare una correzione semplice
alla legge di Lambert per il corpo grigio, in quanto i solidi di radiazione,
in questo caso, hanno forme molto complesse.
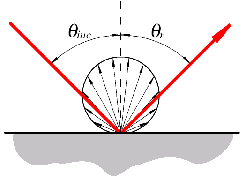
Infine un'ultima applicazione di questa legge si ha in concomitanza con la legge
di Snell, nel momento in cui una parte di intensità di un raggio incidente
viene diffusa anziché essere integralmente riflessa.