Università degli studi di Parma

Corso di laurea in Ingegneria Elettronica,Informatica e delle Telecomunicazioni

Anno Accademico 1999/2000

Lezione del: 20/12/99

Ore: 16.30-18.30

Docente: Prof. Angelo Farina

Autore: Lorenzo Dal Bello

N. di matricola: 121409

Argomenti: 1. Esempio di calcolo degli indici di valutazione del potere fonoisolante con Excel

2. Utilizzo di modelli di calcolo per simulare la propagazione sonora

3. Esercizio: Effetto di una barriera antirumore

Esempio di calcolo degli indici di valutazione del potere fonoisolante con Excel

Dati i valori di isolamento acustico R relativi ad uno scalo aeroportuale, misurati alle frequenze in terzi d’ottava da 125 a 4000 Hz, vogliamo trasformarli in un unico valore equivalente.

Per fare questo utilizziamo i valori di riferimento per il rumore aeroportuale contenuti nella tabella ISO 717 che riportiamo in tabella A:

f	125	157	198	250	315	397	500	630	794	1000	1260	1587	2000	2520	3175	4000
R	33	36	39	42	45	48	51	52	53	54	55	56	56	56	56	56

Tabella A – Valore fonoisolante per rumore aeroportuale (ISO 717)

Attenzione: dal momento che è impossibile reperire gratuitamente le tabelle ISO, i valori qui presenti, così come quelli utilizzati nel foglio di Excel, non sono certi.

Rappresentiamo in un grafico la curva dei valori misurati e quella dei valori di riferimento e facciamo scendere la seconda curva a passi di 1dB, partendo dal valore di 56dB a 500Hz, come è visibile in figura 1.

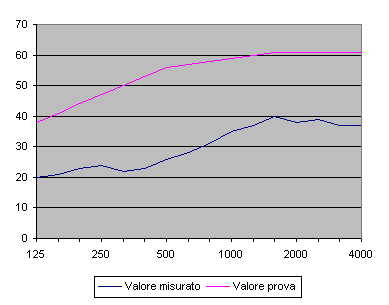
Figura 1 – Grafici delle curve reali e di riferimento di R.

Nel momento in cui la media degli scarti tra i coefficienti misurati e quelli di riferimento è inferiore a 2dB, il valore della curva ISO a 500Hz ci dà il valore equivalente che cerchiamo.

La media degli scarti è calcolabile come: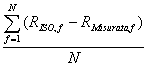 dove N è il numero di misurazioni a diverse frequenze effettuate (nel nostro caso 16).

Includo un foglio di Excel che, una volta inseriti i dati misurati, consente di calcolare l’indice fonoisolante equivalente.

Indici.xls

Per utilizzarlo fare clic sull’immagine qui sopra, rispondendo sì alla richiesta di abilitazione delle macro.

A questo punto si possono inserire i valori misurati nell’omonima colonna o lasciare i valori da me utilizzati; schiacciando sul pulsante calcola verrà determinato l’indice equivalente.

Utilizzo di modelli di calcolo per simulare la propagazione sonora

Esistono alcuni programmi che permettono, mediante la modellazione di ambienti tridimensionali, di simulare la risposta dell’ambiente allo stimolo sonoro.

Uno fra questi è Ramsete, nato dalla collaborazione tra docenti dell’ateneo di Parma, grazie anche al contributo di alcuni studenti.

Ramsete è basato su un metodo di modellazione detto Pyramid Tracing: viene cioè proiettato un fascio divergente di piramidi dalle sorgenti per simulare la propagazione del suono.

Figura 2 – Tracciamento di piramidi dalle sorgenti.

Il pacchetto Ramsete si suddivide in più parti, delle quali segue una breve descrizione accompagnata dall’uso che abbiamo fatto di questi programmi.

Programmi di Pre-Processing:

Material Manager:

Permette di definire i diversi materiali che verranno utilizzati, precisandone colore, coefficiente di assorbimento e valore fonoisolante alle diverse frequenze (da 31.5 Hz a 16 kHz).

È possibile vederne un esempio in figura 3.

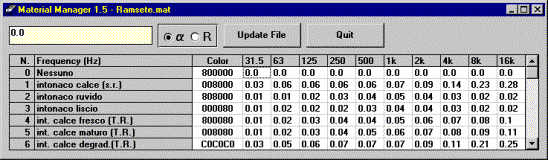
Figura 3 – Esempio di utilizzo del Material Manager.

Noi non abbiamo utilizzato questo strumento, ma abbiamo preferito utilizzare i materiali predefiniti.

Source Manager:

Consente di impostare le caratteristiche di emissione di una sorgente sonora (livelli di potenza, direzione, impedenza, etc.) alle diverse frequenze partendo da files di descrizione generati da altri programmi o direttamente dalle misurazioni effettuate attraverso un analizzatore di spettro real-time.

In figura 4 è mostrato l’utilizzo del Source Manager per la descrizione dei parametri di un altoparlante.

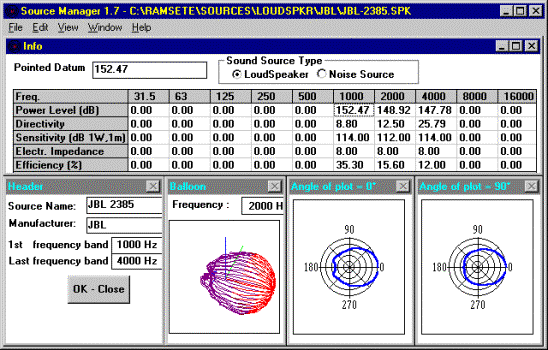
Figura 4 – Definizione dei parametri di un altoparlante attraverso il Source Manager.

Analogamente a prima, abbiamo utilizzato come sorgente una voce umana già impostata.

Ramsete CAD:

È lo strumento di modellazione (compatibile AutoCAD) che permette di ricreare la geometria dell’ambiente che ci interessa simulare, assegnando materiali alle superfici, posizionando le sorgenti sonore, i ricevitori.

Genera un file con estensione .RAY che sarà alla base dell’analisi effettuata; in figura 5 è visibile la ricostruzione tridimensionale di una chiesa.

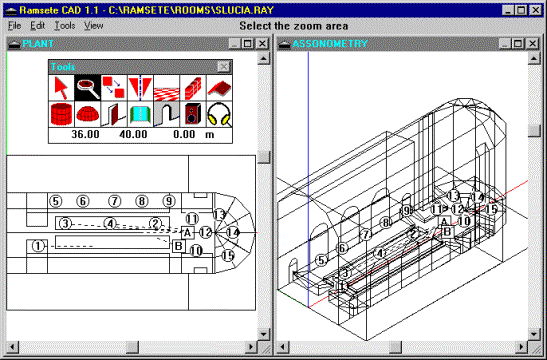
Figura 5 – Ricostruzione di un ambiente con Ramsete CAD.

Durante la lezione abbiamo costruito un modello semplificato dell’aula F dell’università di Parma, definendo dimensioni e posizione reciproca di pavimento, pareti e soffitto.

Per migliorare il modello sono poi state inserite le parti inclinate della pavimentazione e le travi presenti nella parte superiore.

A questo punto abbiamo definito i materiali: cemento per il pavimento, intonaco per le pareti e materiale isolante per il soffitto.

Come sorgente è stata posta una voce umana (soprano) all’altezza di 2m, in posizione approssimante quella reale, puntata verso il lato opposto dell’aula.

I ricevitori sono stati schematizzati mediante una distribuzione lungo una griglia a passo costante di 2m.

Programma di analisi:

Pyramid Tracer:

Questo è lo strumento di calcolo che effettua la simulazione.

Una volta caricato il file generato dal CAD ed impostati alcuni parametri (come tempo di simulazione, precisione richiesta, umidità dell’aria) si può dare il via alla simulazione.

Questa richiede un tempo nettamente inferiore rispetto a metodi di tipo Ray Tracing, proprio a causa del tipo di modellazione matematica.

In figura 6 è mostrata l’interfaccia di Ramsete Trace.

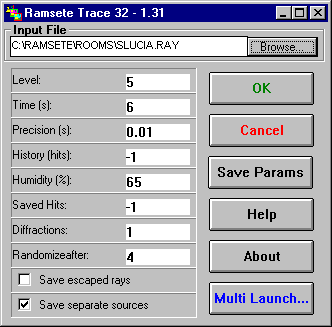
Figura 6 – Esempio di utilizzo di Ramsete Trace.

È possibile anche impostare l’esecuzione di simulazioni multiple in sequenza, come visibile in figura 7.

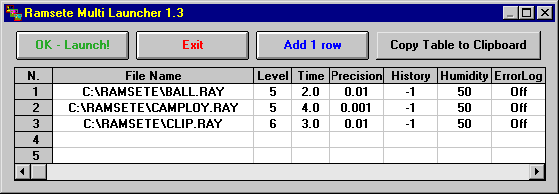
Figura 7 – Esecuzione batch di simulazioni multiple.

Noi abbiamo eseguito il calcolo della risposta dell’aula F impostando un tempo di analisi di 4s e lasciando inalterati gli altri parametri.

Programmi di Post-Processing:

Ramsete Graph:

Caricando il file prodotto dal Tracer, visualizza graficamente le risposte all’impulso, l’integrazione di Schroeder, lo spettro SPL e il tempo di riverberazione per le diverse componenti in frequenza.

È possibile vedere questi dati per ogni ricevitore, o in alternativa avere la risposta media dell’ambiente.

In figura 8 è mostrato un esempio dell’utilizzo di Ramsete Graph.

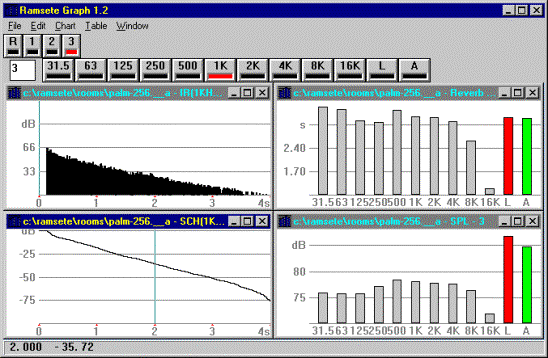
Figura 8 – Rappresentazione dei dati con Ramsete Graph.

Nell’esempio svolto in aula, il riverbero scompariva dopo 1.3 secondi circa; la maggior parte del segnale era contenuta tra 500 e 2000 Hz (ricordiamo che avevamo utilizzato una voce di soprano).

Nella rappresentazione del T20, a frequenze molto basse apparivano valori assurdi (all’incirca 15s): questo è dovuto al fatto che il metodo di calcolo diventa poco attendibile a frequenze estremamente basse o alte.

Ramsete View:

Permette di vedere la geometria della stanza in pianta o in diverse prospettive, creando una mappa di colore che rappresenta graficamente l’andamento di numerosi parametri acustici.

In figura 9 è visibile un possibile utilizzo di Ramsete View.

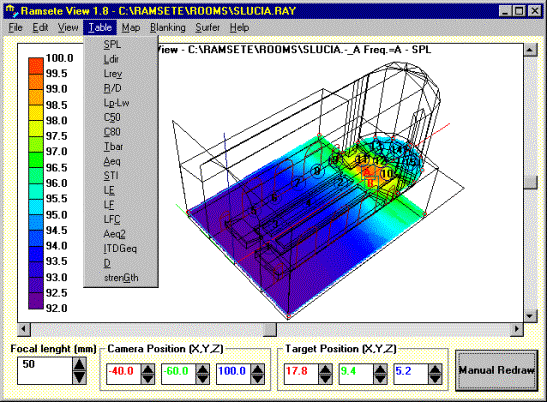
Figura 9 – Rappresentazione dei dati con Ramsete View.

Durante la lezione abbiamo visualizzato una mappa del livello equivalente, constatando che raggiungeva valori di 80dB.

Concentrandoci su un determinato ricevitore, abbiamo determinato il percorso diretto dei raggi e quello riflesso del primo ordine.

Esercizio: Effetto di una barriera antirumore

Una sorgente sonora S posta ad altezza h_S da terra, produce rumore con un livello di potenza dato in funzione della frequenza di emissione riportato in tabella 1.

Un ricevitore R a distanza d dalla sorgente ed altezza h_R da terra misura la potenza del segnale che giunge ad esso.

Si ipotizza che il terreno sia perfettamente assorbente.

Calcolare:

1) Il livello equivalente di potenza che giunge al ricevitore in dB(A).

2) Il livello equivalente dopo che sia stata posta una barriera di altezza h a distanza r₁ dalla sorgente.

Disegno:

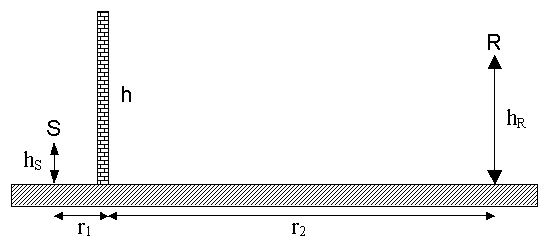Figura 10 – Rappresentazione della posizione reciproca di sorgente, ricevitore e barriera.

Per facilitare la rappresentazione non è stata mantenuta la stessa scala in orizzontale e verticale.

Dati:

h_S = 1m

d = 50m

h_R = 3m

_terr = 1

h = 4m

r₁ = 5m

r₂ = d – r₁ = 45m

f (Hz)	LW (dB)
125	80
250	90
500	78
1000	75
2000	73

Tabella B - Livelli di potenza di emissione della sorgente.

Esecuzione:

1) Il livello lineare equivalente al ricevitore può essere calcolato ricorrendo alla formula del campo libero

L_Eq = L_W – 20 lg(d_SR) – 11

dove d_SR è la distanza lineare tra sorgente e ricevitore.

Si può osservare che il termine aggiuntivo che differenzia il livello emesso da quello che giunge al ricevitore dipende solo dalla distanza (e non dalla frequenza del segnale).

Perciò calcoliamo la distanza tra sorgente e ricevitore con il teorema di Pitagora:

Il termine aggiuntivo diventa quindi pari a

– 20 lg(50.04) – 11 = 45 dB

e la formula del campo libero diventa

L_Eq = L_W – 45

Per ottenere i valori secondo la curva di risposta A utilizzo i livelli di ponderazione alle diverse frequenze riportati in tabella C.

f (Hz)	125	250	500	1000	2000
AW (dB)	-16.8	-8.6	-3	0	+1.2

Tabella C – Livello di attenuazione in potenza dato dalla curva A.

Il livello equivalente viene calcolato applicando entrambe le correzioni (quella dovuta alla distanza tra sorgente e ricevitore e quella dovuta all’utilizzo della ponderazione A).

L_Eq,A = L_Eq – A_W = L_W – 45 – A_W

Trascrivo tutti i risultati in tabella D:

F	LW	LEq	AW	LEq,A
125	80	35	-16.8	18.2
250	90	45	-8.6	36.4
500	78	33	-3	30
1000	75	30	0	30
2000	73	28	+1.2	29.2

Tabella D – Livello equivalente ponderato A e dati necessari al suo calcolo.

Infine, ottengo il livello sonoro totale (senza barriera) sommando i valori alle singole frequenze (utilizzando la formula per la somma di quantità logaritmiche, quali sono i deciBel):

L_Eq,A,Tot = 10 lg (10^1.82 + 10^3.64 + 10³ + 10³ + 10^2.92) = 38.6 dB(A)

2) La barriera produce una attenuazione che varia in funzione della frequenza.

È possibile calcolare questa differenza, applicarla ai livelli equivalenti lineari ed infine applicare la curva di correzione A.

Ma è molto più rapido applicare le correzioni ai livelli L_Eq,A precedentemente calcolati.

Per farlo utilizziamo gli studi di Maekawa: secondo una delle formulazioni che diede al problema, dato uno schermo sottile di lunghezza indefinita e supposte puntiformi le sorgenti (caso nel quale rientra il nostro esercizio), la differenza di livello nel momento in cui si pone lo schermo tra sorgente e ricevitore si calcola con

N, numero di Fresnel, è dato da 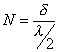dove rappresenta la lunghezza d’onda del segnale sonoro, è la differenza tra il cammino diffratto e quello diretto.

Indicando con d_SR la distanza tra sorgente e ricevitore, con d₁ quella tra la sorgente e la sommità della barriera e con d₂ la distanza che separa barriera e ricevitore si può ottenere come differenza tra queste come mostrato in figura 11:

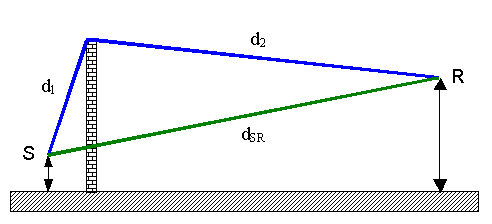
Figura 11 – Differenza tra cammino diffratto e diretto.

Nel nostro caso, applicando più volte il teorema di Pitagora, otteniamo:

Perciò =d₁ + d₂ - d_SR = 5.83 + 45.01 – 50.04 = 0.8m

Consideriamo la relazione tra lunghezza d’onda e frequenza di un suono che si propaga in aria: dove è la lunghezza d’onda, f la frequenza e c è la velocità del suono in aria (c = 340 m/s).

Utilizzandola il numero di Fresnel può essere riscritto come

Si può notare come N dipenda dalla frequenza del suono emesso: per stabilire l’attenuazione di una barriera non basta perciò conoscere i dati fisici di questa, ma bisogna conoscere anche lo spettro del segnale da schermare (ad esempio, una barriera utilizzata su tratti ferroviari non costituirà un rimedio altrettanto efficace al rumore autostradale, molto più ricco di basse frequenze).

Perciò, sostituendo, la relazione di Maekawa diventa:

Possiamo quindi calcolare alle diverse frequenze e utilizzando la relazione

ricavabile direttamente otteniamo i livelli ponderati A al ricevitore, attenuati dalla barriera, che riportiamo in tabella E.

f	LEq,A		LEq,Barr,A
125	18.2	11.7	6.5
250	36.4	14.2	22.2
500	30	17	13
1000	30	19.9	10.1
2000	29.2	22.8	6.4

Tabella E - Livello equivalente con barriera ponderato A e dati necessari al suo calcolo.

Analogamente al primo caso, il livello sonoro totale con la barriera si ottiene sommando i valori alle diverse frequenze:

L_{Eq,Barr,A,Tot} = 10 lg (10^0.65 + 10^2.22 + 10^1.28 + 10^1.01 + 10^0.64) = 23.1 dB(A)

Si può perciò calcolare l’attenuazione prodotta dalla barriera: