ACUSTICA ED ELETTROACUSTICA
Generalità
L'acustica ha avuto un'evoluzione
molto rapida negli ultimi dieci anni, in particolar modo a partire dal
'91, principalmente per motivi di tipo legale. Sono infatti uscite in Italia
delle leggi precise in materia che, accompagnate dalla disponibilità
di strumenti di elaborazione sempre più potenti, hanno permesso
una rapidità di sviluppo sconosciuta alle altre discipline scientifiche.
Tanto per fare un esempio, l'acustica ha avuto negli ultimi dieci anni
lo stessa crescita che ha avuto l'informatica in un ventennio. E questo
ritmo d'avanzamento è tale tuttora.
Il suono: definizione
Il suono è un fenomeno di
trasporto energetico (quindi dove si ha un movimento di energia meccanica
da un punto ad un altro) ma non di materia; esso richiede un mezzo elastico
in cui propagarsi (mentre non può in sua assenza, come nel vuoto),
dove per mezzo non si deve intendere necessariamente l'aria, ma qualsiasi
sostanza, sia essa un liquido, un solido od un gas.

Fig. 1 - Sveglia
Una sveglia posta sotto una campana
di vetro in cui viene fatto il vuoto viene fatta suonare, ma all'interno
della campana il suono non è udibile proprio perché l'assenza
di un mezzo ne impedisce la propagazione.
Esso non è però l'unica
forma di trasporto di energia meccanica esistente; se per esempio alziamo
ed abbassiamo l'estremo di una lastrina di metallo all'interno del solido
si propagheranno onde che non saranno solamente onde sonore, ma anche di
altro tipo.
Le onde sonore hanno una caratteristica
fondamentale: le particelle della materia coinvolta nel trasporto del suono
fluttuano intorno ad una posizione di equilibrio, ma a differenza di altri
tipi di onde il loro moto non è perpendicolare alla direzione dell'onda,
ma parallelo; per questo si parla di onde longitudinali. Un esempio
di onde non longitudinali (trasversali) può essere rappresentato
dalle onde del mare: in questo caso infatti la direzione del moto delle
particelle d'acqua è dall'alto verso il basso, perpendicolare alla
direzione di propagazione dell'onda (che si trova sul piano costituito
dalla superficie dell'acqua).
Attenzione, però: non solamente
le onde sonore trasmettono il suono! Se per esempio considero il caso in
cui una persona parla in una stanza, sappiamo che la sua voce potrà
essere udita (se il locale non è eccessivamente insonorizzato) anche
in una stanza adiacente; in questo caso però le onde sonore si propagano
nelle infrastrutture sotto forma di altre onde di tipo trasversale (di
taglio, o di riflessione, ad esempio), le quali poi irradiano onde sonore
nell'ambiente ricevente.
Si è solito considerare il
suono nell'aria; sappiamo però che esso, che è costituito
da onde longitudinali all'inizio e alla fine, può propagarsi sotto
altre forme durante il suo cammino. E proprio questo fatto deve essere
considerato molto attentamente, poiché queste altre onde possono
essere un problema nello studio dell'isolamento acustico: tali onde (principalmente
trasversali, anche se possono essere di altro tipo), infatti, sono studiate
solamente in sismologia.
Sappiamo infatti dallo studio dei
terremoti che alcuni tipi di onde si diffondono più velocemente
delle altre: ad esempio le onde s, che danno origine alle cosiddette
"scosse di avvertimento", si propagano più velocemente delle altre.
Possiamo quindi a questo punto definire la velocità di propagazione
di un'onda.
Il suono: velocità
La velocità del suono nell'aria
è praticamente costante (anche se varia debolmente con la temperatura);
essa viene indicata con la lettera c e corrisponde a circa
343
m/s. Nei mezzi non dispersivi (come l'aria) la velocità
non
dipende dal tipo di segnale (cioè dalla forma d'onda), né
dall'ampiezza di vibrazione.
Quindi dobbiamo distinguere la velocità
del suono (intesa come velocità di propagazione dell'onda sonora)
dalla velocità delle particelle. A tale proposito possiamo avvalerci
dell'esperimento riprodotto in figura:
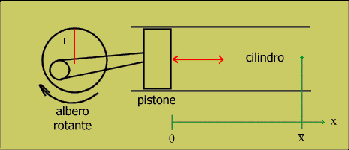
Fig. 2: Esperimento
Un albero rotante che si muove con
velocità angolare w, viene collegato
ad un pistone libero di muoversi all'interno di un cilindro pieno di aria;
questo sistema genera onde meccaniche di tipo longitudinale (cioè
simili alle onde sonore), e ci permette di capire la dinamica con la quale
tali onde si propagano.
Il moto del pistone sarà
di tipo armonico con oscillazioni di ampiezza sinusoidale date dalla seguente
legge (r indica il raggio dell'albero rotante, e
A(t)
la posizione del pistone rispetto alla posizione iniziale):
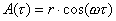 (1)
(1)
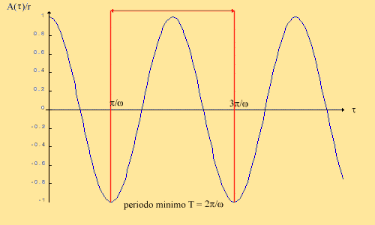
Fig. 3 - Grafico delle oscillazioni in dipendenza dal tempo
Le particelle d'aria più prossime
al pistone, per l'ipotesi di aderenza vista in fluidodinamica, seguono
il moto di quest'ultimo perciò la velocità può essere
ricavata derivando la legge precedentemente vista per l'ampiezza delle
oscillazioni del pistone:
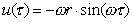 (2)
(2)
La velocità delle particelle
è quindi di tipo sinusoidale con valor medio nullo, il che significa
che le particelle più vicine al pistone si muovono avanti e indietro
nel tubo rimanendo aderenti al pistone. La (2) è detta legge
del moto armonico.
Per tale tipologia di moto sono definite due grandezze,
il periodo e la frequenza. Il primo (si misura in secondi,
s)
è il tempo impiegato, nel nostro caso, dal pistone ad effettuare
un'intera rotazione; la seconda (si misura in hertz, hz) è
il reciproco del periodo.
Non tutti i suoni sono di tipo armonico.
Dal momento che ogni particella
è dotata di una massa e di una elasticità, la possiamo considerare
come una massa infinitesima che spinta dal pistone trasmette a sua volta,
per mezzo di una molla infinitesima, il moto ad un'altra massa infinitesima
(cioè ad un'altra particella).
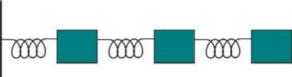
Fig. 4 - Masse collegate da molle
Lo strato di particelle aderenti al
pistone agisce elasticamente trasmettendo la spinta al secondo strato dopo
un certo istante di tempo; quindi l'energia meccanica, in altre parole
(per analogia) l'onda sonora, non si propaga a velocità infinita
ma con la velocità
c che è stata definita prima. La
velocità della generica particella (che, è importante ripeterlo,
non
è la velocità dell'onda) presente nel tubo in corrispondenza
dell'ascissa
x è ricavabile tramite una traslazione nel tempo
della legge vista in precedenza.
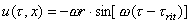 (3)
(3)
dove trit
viene detto ritardo di propagazione e indica il tempo di ritardo
dell'onda sulla particella alla generica ascissa x:
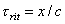 (4)
(4)
La sua posizione risulta:
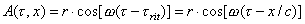 (5)
(5)
Per fare un esempio, la voce di una
persona che parlasse dal fondo di un'aula lunga 13 metri si udirebbe all'altro
capo della stanza dopo un ritardo di:
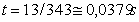
Questo tempo non è sufficiente
per darci l'impressione che quanto sentito sia fuori sincronia con i movimenti
labiali di chi parla; se però considero una distanza maggiore (ad
esempio 130 metri), avendo un ritardo di 0,379s, quanto da me udito sarà
sfasato rispetto a quanto pronunciato in quel momento di una sillaba (normalmente
si pronunciano tre sillabe al secondo). Come sappiamo dalla psicoacustica,
infatti, il nostro sistema uditivo ci permette di percepire un'onda sonora
in un lasso di tempo compreso tra i 50 ed i 150 ms (secondo il tipo di
suono: quelli più gravi e forti sono percepiti prima degli altri,
a causa di fattori evolutivi); un suono che quindi ci raggiunge in un tempo
inferiore ai 100 ms viene da noi percepito praticamente come "istantaneo".
Il tempo calcolato negli esempi
in realtà si riferisce al ritardo della sola onda sonora diretta
e non a quello di tutte quelle che subiscono effetti di riflessione, che
in generale possiedono un ritardo maggiore rispetto all'onda diretta. La
voce della persona arriverebbe quindi all'orecchio dell'ascoltatore con
una sorta di coda sonora derivante dalla somma di tali effetti.
Fig. 5 - Coda del tempo
Si capisce quindi che a differenza
di altri tipi di onde (come quelle elettromagnetiche, ad esempio), il ritardo
di propagazione del suono è riscontrabile in molte situazioni, perciò
è di importanza fondamentale rapportare lo studio del suono alla
scala dei tempi; questo non si faceva prima di dieci anni fa, quando l'analisi
del suono era relativo solamente alla sua pressione e lo studio avveniva
solamente in frequenza, senza valutare il suo andamento nel tempo.
Il suono: pressione
Abbiamo precedentemente detto che,
affinché il suono possa diffondersi, il mezzo attraverso cui viaggiano
le onde sonore deve essere elastico. Ritornando al caso del pistone mobile,
possiamo affermare che, essendo l'aria un mezzo elastico, la sua compressione,
supposta adiabatica, dovuta all'avanzamento del pistone, viaggia con velocità
finita e quindi, ad un determinato istante di tempo e ad un'opportuna distanza
dal pistone, esisterà sempre uno strato di particelle rimaste ferme
che costituisce una barriera all'avanzamento delle particelle perturbate
dal moto del pistone. Si ha il cosiddetto fenomeno di confinamento inerziale
il quale fa sì che, sebbene non vi sia una parete solida, il volume
del gas diminuisca e che di conseguenza aumenti la pressione. Considerando
l'aria come un gas perfetto sappiamo valere le seguenti relazioni:
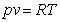 (6)
(6)
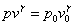 (7)
(7)
dove p0 e v0 rappresentano rispettivamente
i valori di pressione e di volume in condizioni standard.
E' da notare che la sovrapressione
determinata dal campo sonoro è pressoché irrilevante se confrontata
alla pressione dell'aria: mentre quest'ultima ha solitamente una pressione
intorno ai 100.000 pa, l'onda sonora genera una pressione di pochi
pa.
E' facile a questo punto ricavare
la velocità in funzione della densità (r);
posso infatti scrivere:
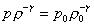 (8)
(8)
Quindi
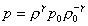 (9)
(9)
Derivando rispetto alla densità:
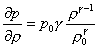 (10)
(10)
Studiando la derivata nell'intorno
dell'origine abbiamo:
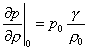 (11)
(11)
Si può dimostrare che l'ultimo
risultato ottenuto corrisponde dimensionalmente al quadrato di una velocità
e che (essendo c la velocità del suono):
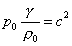 (12)
(12)
e quindi
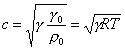 (13)
(13)
Relazioni analoghe possono essere
dimostrate per i liquidi e per i solidi. Per i liquidi:
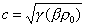 (14)
(14)
essendo
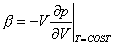 (15)
(15)
il modulo
di compressibilità isoterma per i liquidi, mentre per i solidi:
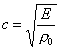 (16)
(16)
dove E è il "modulo
elastico".
Abbiamo quindi gli strumenti per
ricavare la velocità del suono nelle varie sostanze; I valori più
importanti
sono riportati nella seguente tabella:
|
Mezzo
|
Velocità del suono [m/s]
|
|
Acqua
|
1480
|
|
Quarzo
|
5486
|
|
Acciaio
|
6096
|
|
Azoto (N2)
(a T = 27°C e p = 1 bar)
|
353
|
|
Azoto (N2)
(a T = 27°C e p = 100 bar)
|
379
|
|
Idrogeno (H2)
|
1281
|
I differenti valori di velocità per l'azoto
ci rivelano che questo tipo di gas non può essere considerato perfetto,
perché se così fosse la velocità non dovrebbe variare
con la pressione.
E' importante notare l'alto valore
dell'acqua; oltre ad essere abbastanza elevato, l'acqua ha un bassissimo
coefficiente
di perdita: il suono infatti può percorrere in acqua anche centinaia
di chilometri prima di perdere ampiezza.
Questa velocità ha anche
un aspetto negativo: infatti il tempo necessario a raggiungere un orecchio
è pressoché uguale a quello necessario a raggiungere l'altro.
Questo non ci permette, in acqua,
di localizzare correttamente l'origine dei suoni.
Il nostro sistema uditivo è
infatti "calibrato" per ascoltare suoni provenienti dall'aria: in base
al ritardo che impiega un suono a giungere alle nostre orecchie (IDT,
interaural
delay time o ILD, interaural level difference per le
alte frequenze), capiamo da dove arriva.
In acqua, dove la velocità
del suono è diversa, il nostro sistema uditivo non riesce a capire
dove si trova la sorgente; e però sufficiente utilizzare un dispositivo
come quelli utilizzati una volta dai sottomarini per ovviare a questo problema.
E' però necessario introdurre
prima il concetto di lunghezza d'onda.
Il suono: lunghezza d'onda
Anche questa definizione (come quella
di periodo e di frequenza, oltre che di pulsazione) è applicabile
solamente ad onde sonore di tipo sinusoidale.
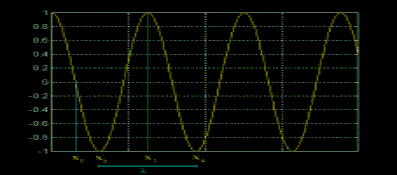
Fig. 6 - Funzione di tipo sinusoidale
Se noi andiamo a "fotografare" l'onda
in un istante t = t1,
scopriamo che in x1 è nulla, in x2
è minima, in x3 è massima, in x4
è ancora minima, e così via…
Si nota subito che essa assume lo
stesso valore sia in x1 che in x4,
e questa distanza viene definita lunghezza d'onda (e viene solitamente
indicata con la lettera greca lamba, l):
la minima distanza fra due punti che assumono lo stesso valore in un determinato
istante.
Se noi invece fotografassimo l'onda
in un punto x = x1, avremmo ancora una sinusoide,
anche se in funzione dello spazio. E così come il periodo indica
un'oscillazione completa nel tempo, così la lunghezza d'onda rappresenta
un'oscillazione completa nello spazio.
Il periodo viene quindi definito
come:
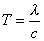 (17)
(17)
e quindi
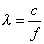 (18)
(18)
Le frequenze percepibili dall'orecchio
umano sono quelle comprese tra 20 hz e 2000 hz (tre decadi).
Queste le relazioni tra alcune frequenze e lunghezze d'onda in aria:
|
f
|
l [m]
|
|
20
|
17
|
|
1000
|
0,34
|
|
20000
|
0,017
|
Un ostacolo è tale per un'onda se e solo se
è superiore alla lunghezza d'onda.
Tornando al problema della localizzazione
delle sorgenti di rumore sott'acqua, essendo la velocità in acqua
circa cinque volte quella in aria, è sufficiente che si ascoltino,
dall'interno di un involucro grande cinque volte la nostra testa (per mezzo
di strumenti chiamati idrofoni) i suoni percepiti agli estremi di
tale oggetto; in tale modo, inoltre, si mantiene la proporzione anche con
l'effetto schermante della nostra testa. Siamo così in grado di
localizzare correttamente l'origine del suono.
Il suono: l'analisi
Nello studio dei segnali sonori
sono di importanza fondamentale la velocità e la pressione dell'onda
in funzione del tempo. La pressione rappresenta l'energia immagazzinata
in forma elastica, la velocità rappresenta l'energia cinetica.
Se vado a diagrammare nel tempo la pressione e la velocità
relative all'esempio precedente (quello del pistone), avremo un grafico
di questo tipo:
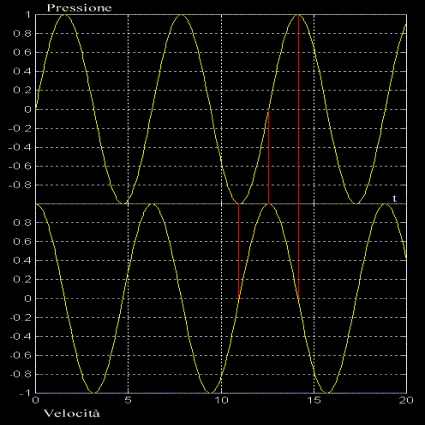
Fig. 7 - Grafico velocità/pressione
Dal punto di vista fisico, come si
può osservare dal disegno, si ha una continua oscillazione tra energia
cinetica ed energia potenziale.
Gli strumenti che misurano la pressione
e la velocità dell'aria si chiamano rispettivamente
microfoni
e anemometri. Esistono dei trasduttori integrati, formati da più
trasduttori indipendenti, che possono fornire oltre al valore della pressione
le componenti cartesiane del vettore velocità.
Ma si pongono ora due problemi:
il primo è quello di valutare il valore medio della pressione nel
tempo, il secondo è quello di relazionare tale valore con la capacità
di percezione umana, che si basa su una scala logaritmica.
La soluzione ovvia al primo problema
sarebbe di calcolare il valor medio in un periodo di tempo di circa 50
ms
(corrispondente al tempo di percezione umana), scrivendo:
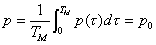 (19)
(19)
Questo procedimento è però
inutile, poiché tale valore continua ad oscillare intorno a p0
e sarà costante per qualsiasi finestra di tempo io consideri.
Ci serve un descrittore che sia
differenziale rispetto alla pressione, e questo può essere un microfono,
il quale non ci dà informazioni proporzionali a p, ma a (p-p0).
Ma nemmeno questo è sufficiente: infatti calcolando il valor medio
in questo modo otterrei sempre zero.
Allora è necessario valutare
il problema in termini energetici.
Sappiamo che l'energia potenziale
è proporzionale al quadrato della pressione, e che l'energia cinetica
è proporzionale al quadrato della velocità.
I valori medi energetici possono
essere calcolati come media RMS (root mean square), detto
anche valore medio efficace, che risultano essere:
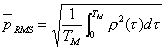 (20)
(20)
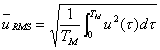 (21)
(21)
Per mezzo di queste formule, otteniamo
effettivamente un valore di pressione medio che corrisponde abbastanza
bene a quanto percepito dal nostro orecchio. La loro validità è
indipendente dalla frequenza di campionamento considerata.
L'effettuazione di tali calcoli
è, grazie alla potenza degli strumenti di calcolo a nostra disposizione
al giorno d'oggi, banale; tali strumenti inoltre dispongono di convertitori
analogico-digitali che ci permettono di ottenere la forma d'onda con frequenze
di campionamento molto elevate (si parte dai 44.100 hz del formato
CD fino ad arrivare ai 96.000 hz e oltre delle schede audio dei
PC).
Non era banale qualche anno fa,
quando si avevano a disposizione solamente strumentazione di tipo analogico;
si scelse allora la strada di utilizzare dei circuiti dotati di memoria
infinita, circuiti basati su una coppia resistenza-condensatore chiamati
mediatori RC (fig. 8).
Sono circuiti il cui segnale in
uscita non segue le leggi indicate dalle formule (20) e (21).
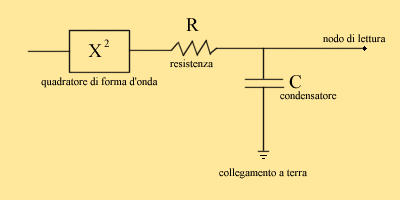
Fig. 8 - Mediatore RC
Il condensatore serve a smorzare le
oscillazioni del circuito scelto, quindi l'uscita del condensatore viene
collegata all'indicatore a lancetta che indica il valore medio efficace
(anche se non è corretto chiamarlo in tale modo); questo condensatore
viene caricato tramite una resistenza che prende il segnale dall'uscita
del circuito quadrato, collegato a sua volta con un microfono (e, prima,
eventualmente, anche ad un amplificatore). La coppia RC viene chiamata
circuito
di memoria.
Facendo il controllo dimensionale
del prodotto RC, otteniamo un tempo; tale prodotto si chiama costante
di tempo (e viene indicata con t0).
Il segnale di uscita, in funzione
del segnale d'entrata risulta essere:
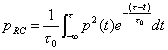 ,
, 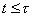 (21)
(21)
dove poniamo
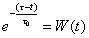 (22)
(22)
Il primo membro della (22) è
detto weight (peso). Graficamente il suo andamento nel tempo è
il seguente:
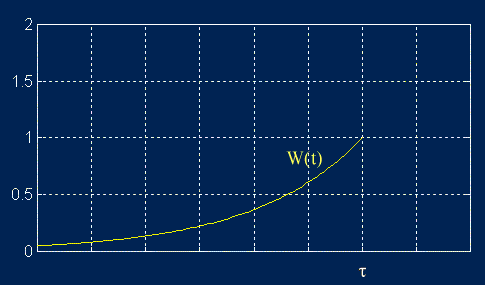
Fig. 9 - Andamento della funzione
weight
A seconda della memoria (cioè,
in sostanza, la costante di tempo) del circuito mediatore, essi vengono
tradizionalmente classificati in:
SLOW --> RC = 1s
FAST --> RC = 0,125s
L'effetto pratico delle differenti
impostazioni e' che la lancetta indicatore del primo avrà la tendenza
a mantenere per più tempo il valore analizzato; il secondo invece
tenderà a diminuire (a "dimenticare") tale valore più rapidamente.
Quanto analizzato dal nostro sistema
uditivo è simile alla rappresentazione FAST.



![]() (2)
(2)
![]() (3)
(3)![]() (4)
(4)![]() (5)
(5)![]()

![]() (6)
(6)
![]() (7)
(7)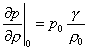 (11)
(11)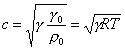 (13)
(13)![]() (14)
(14)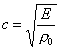 (16)
(16)

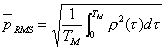 (20)
(20)
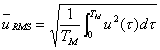 (21)
(21)
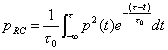 ,
, 