Roberto Bianchi mat.118871 Lezione del 14/12/1999 ore 14.30-16.30

Universitá degli Studi di Parma

Nello studio dell’acustica l’ambiente viene schematizzato con il concetto di scatola nera: un oggetto avente un ingresso ed una uscita ad esso correlata ma il cui funzionamento interno non é noto.

Si presuppone che il campo acustico in un ambiente sia lineare.

Un sistema si dice lineare se l’uscita é una funzione lineare dell’entrata ovvero se vale il principio di sovrapponibilitá degli effetti .

Il principio di sovrapponibilitá degli effetti si puó esprimere cosí: dati due ingressi generici A e B e le loro relative uscite C e D, ottenute applicando singolarmente gli ingressi, applicando nel sistema l’ingresso A+B si ottiene l’uscita C+D.

Tab.1: Mostra il comportamento di un sistema lineare.

Inoltre si presuppone che i sistemi studiati siano tempo invarianti, cioé indipendenti dal tempo.

Nell’ambito di queste ipotesi si applica il concetto matematico di risposta all’impulso. La formulazione di questa teoria é particolarmente semplice nel dominio digitale dei segnali campionati.

Il segnale in questo dominio é rappresentato cosí: l’intervallo di variabilita’ della tensione viene diviso in 2 (dove n é il numero di bits usati nella rappresentazione) sottointervalli rappresentati ciascuno dal proprio valore medio; periodicamente il segnale analogico viene misurato (campionato) ed a seconda dell’intervallo in cui cade la tensione il campione assume il valore medio dell’intervallo.

Quindi la rappresentazione di un segnale nel dominio digitale é semplicemente un insieme ordinato di numeri interi. Si definiscono inoltre alcune grandezze che influenzano la rappresentazione digitale: frequenza di campionamento n , periodo (é l’inverso della frequenza di campionamento) D t .

Tab 2. Esempio di segnale nella rappresentazione digitale (e binaria) ad 8 bit.

Come si é visto il segnale entra nel sistema come un vettore di numeri (il nome dei vettori verrá scritto minuscolo in neretto) ed esce dal sistema come un altro vettore di numeri con la stessa frequenza di campionamento. Chiamando x il vettore di numeri in entrata e y quello in uscita essi possono essere rappresentati cosí:

Bisogna notare come i dati in uscita siano "legati" ai dati in ingresso: in particolare avendo in ingresso una sequenza di zeri (silenzio) seguita da numeri non nulli a loro volta seguiti da zeri, in uscita si avrà una sequenza simile alla prima salvo che per il numero di zeri all’inizio ed alla fine e per i valori dei campioni.

Questa disparitá nel numero di zeri precedenti e seguenti i due segnali deriva dal fatto che la risposta del sistema non é istantanea, né quando il sistema viene eccitato (attacco del suono), né quando il sistema ritorna allo stato iniziale (coda del suono).

In termini matematici questo si esprime dicendo che y non é funzione solo di x ma di un certo numero di campioni in entrata precedenti a x. Nel dominio digitale questo viene espresso dall’equazione:

y=xh + xh+ xh + xh + ……+ xh

dove m é il numero dell’ultimo elemento di cui si ha memoria.

Questa operazione si definisce convoluzione e si usa la notazione:

y=xh

I coefficienti rappresentano quindi la "caratteristica" del sistema. Guardando a questi coefficienti come ad una forma d’onda, questa rappresenta la risposta all’impulso del sistema ed ha la stessa frequenza di campinamento dei dati in ingresso. Per riprodurre questo comportamento del sistema i sistemi digitali di riproduzione e studio degli ambienti hanno a disposizione della memoria in cui i campioni vengono immagazinati. La natura del problema studiato implica la necessitá di avere una memoria "equivalente" a tempi che possono arrivare ad alcuni secondi. Con un semplice calcolo, ipotizzando una frequenza di campionamento di 44.100 Hz (la frequenza dei CD audio commerciali), si nota come una memoria di 5 secondi richieda l’utilizzo di 5 * 44100=220500 bytes.

Tale calcolo é realistico, considerando il fatto che valori tipici di memorie dei sistemi digitali di studio e simulazione degli ambienti, variano nell’ordine di 10-10 bytes.

Si possono fare due considerazioni: intanto un notevole aumento della memoria richiesta rispetto a sistemi digitali dedicati allo studio ad esempio di fenomeni elettrici, inoltre la notevole mole di calcoli che questo tipo di trattazione richiede, cosí notevole da non poter essere svolta tuttora in tempo reale e comunque tecnologicamente irrealizzabile fino a pochi anni fa.

La tecnica di misura dei coefficienti h é teoricamente molto semplice: basta infatti immettere nel sistema la d di Dirac ovvero un segnale costituito da un uno seguito solo da numeri nulli.

Convolvendo la d di Dirac si ottengono quindi:

y=1*h+ 0*h+0*h=h

y=0*h+ 1*h+0*h=h

y=0*h+ 0*h+1*h=h

Ad ogni passo di campionamento si ottiene quindi un coefficiente h.

Questo tipo di misurazione, benché teoricamente semplicissima, é praticamente irrealizzabile: dovrei essere capace di produrre un impulso brevissimo e di elevata potenza (per una buona misurazione ho bisogno di almeno 60 db oltre il rumore di fondo).

Una possibile soluzione é l’uso di esplosivi (una pistola caricata a salve) che peró non dá un segnale che dura solo un periodo di campionamento ma arriva a qualche decina di periodi.

Per ovviare a questo inconveniente si puó convolvere il segnale di risposta dell’ambiente con sé stesso rovesciato sull’asse dei tempi in modo da far diventare primo l’ultimo campione etc.

Questa tecnica prende il nome di Time Reversal Mirror. Questo porta ad avvicinarsi alla d di Dirac ma non al suo raggiungimento. Se col TRM ottenessimo effettivamente la d di Dirac viste le proprietá di commutativitá della convoluzione, basterebbe convolvere il segnale in uscita con il segnale in ingresso rovesciato sui tempi per ottenere la risposta all’impulso del sistema.

Da queste considerazioni nasce l’idea di deconvolvere il segnale con un segnale casuale come ad esempio il rumore bianco. Questo si fa sperando di trovare un x tale che x x sia uguale alla d di Dirac. Ammesso di riuscire a trovare x si otterrebbe:

purtroppo peró e molto difficile riuscire a trovare x.

Si puó peró provare a passare nel dominio delle frequenze (in maiuscolo i vettori rappresentati in frequenza):

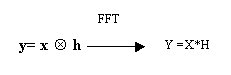
Notiamo che mentre nel dominio del tempo sono necessarie m convoluzioni ( a loro volta costituite da m somme ed m prodotti ) quindi un numero di operazioni dell’ordine di m, in frequenza ogni armonica viene semplicemente moltiplicata per un coefficiente per un totale di m operazioni (si noti come la trasformazione e antitrasformazione siano operazioni con un costo di calcolo limitato). Inoltre in frequenza l’operazione di ricerca dei coefficienti H é estremamente semplice, infatti essi sono semplicemente il quoziente fra Y e X.

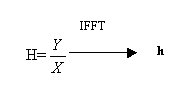
In particolare si definisce H funzione di trasferimento del sistema mentre h é la risposta all’impulso.

Esiste peró un problema fondamentale: il risultato e’instabile; infatti nel caso di una frequenza con coefficiente nullo il coefficiente H relativo diverge. Si puó ovviare a questo problema facendo una media con varie misurazioni e scegliendo un segnale in ingresso che dia energia su tutte le frequenze,tipicamente il rumore.Un altro problema é che si deve usare una FFT di lunghezza adeguata al tempo di risposta del sistema.Infatti, come detto prima, si deve ripete il segnale nel tempo per ottenere dati per la media e usare una fraquenza di ripristino che non porti sovrapposizioni dei segnali in uscita ed inoltre una FFT che comprenda ogni volta la risposta all’impulso di una singola ripetizione; altrimenti si verifica il fenomeno del Time Aliasing.

Un programma commerciale che é basato sull’uso del rumore é Smaart Pro della JBL.

Al posto del rumore si puó peró scegliere il segnale in ingresso in maniera piú furba, mantenendo le caratteristiche utili (la presenza di tutte le frequenze con coefficienti non nulli) ma cercando di ottenere ulteriori vantaggi.

Un segnale particolarmente "intelligente" deriva dalla teoria dei numeri e prende il nome di MLS (Maximum Length Sequence). Questo segnale é una sequenza binaria costruita tramite uno Shift register (registro a scorrimento):

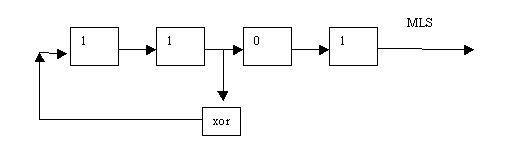
Esempio di Shift register a 4 bit, i numeri scorrono a destra ad ogni passo.

Con opportuni valori iniziali e un corretto posizionamento dell xor si ottiene un MLS. Si possono fare varie osservazioni su questa sequenza:

· essendo nota in partenza si trova matematicamente MLS con l’inversione di Hadamard;essendo inoltre MLS un segnale binario é particolarmente facile la convoluzione (poiche’ spariscono le moltiplicazioni)

· grazie alla semplicitá di questo segnale é possibile fare la convoluzione nel dominio dei tempi in tempo reale

· siccome il segnale in entrata é generato direttamente non deve piú essere campionato e quindi si può usare una scheda di campionamento ad una sola entrata

· inoltre essendo lo spettro sonoro dell MLS piatto come quello del rumore posso fare anche l’analisi in frequenza.

Si dimostra che la lunghzza di una MLS é di 2-1 dove n é il numero di celle dello shift register. In acustica in particolare, si usano normalmente shift registers a 16 o piú celle ricavando MLS di 65535 campioni (caso 16 celle) o superiori (ovviamente peró si può ripetere il segnale).

Questa tecnica, inventata nel 1975 dal tedesco Alrutz, é stata la piú usata fino a circa un anno fa. Questo anche grazie alla diffusione di una scheda, costruita nel 1989 dall’americano Douglas Rife, che implementava per via hardware lo shift register e corredata da un software chiamato MLSSA (melissa) particolarmente potente,tanto da essere tuttora usato. Gli svantaggi di questa tecnica sono la fortissima dipendenza dalle caratteristiche di linearitá del sistema. Infatti nel caso di non-linearitá anche lievi possono apparire echi inesistenti e si puó avere la cancellazione delle alte frequenze a causa del loro sfasamento reciproco che le puó portare in controfase. Purtroppo quindi questa tecnica puó essere usata solo con riproduttori audio molto fedeli e per un tempo non troppo lungo, infatti il riscaldamento degli altoparlanti comporta una perdita di fedeltá e conseguentemente di linearitá.

Attulmente, comunque, la tecnica migliore é quella dello sweep. Il segnale cosí definito é composto da un seno che parte dalle frequenze basse e sale verso l’alto.Questa tecnica presenta il vantaggio che

S=segnale di sweep

S=S rovesciato sull’asse dei tempi.

Come contropartita di questa comoditá perdo peró i vantaggi sulla convoluzione. Per riottenere la velocitá di calcolo della convoluzione posso passare in frequenza.

Per effettuare le misure é necessario avere: un computer dotato di scheda audio full duplex (ovvero abilitata a registrare da un canale mentre riproduce su di un altro), un software di hard disk recording funzionante in modalitá multitraccia (Cool Edit pro oppure Cakewalk Pro Audio o altri), un impianto di riproduzione ed un microfono.Inoltre é utile un editor audio abbastanza completo per la visualizzazione dello spettrogramma e della ETC(energy time curve).

Cablaggio e funzionamento dell’impianto usato per le misure: il software funge sia da riproduttore del segnale di eccitazione sia da registratore del segnale di risposta dell’ambiente; questo fa nascere la necessitá di un computer che supporti il full duplex.

L’impianto é molto semplice, infatti all’uscita della scheda audio si collega l’impianto di riproduzione (nel mio caso due speaker da concerto amplificati con un amplificatore esterno) e all’entrata di registrazione della scheda audio si collega il microfono (che se passivo potrebbe necessitare di una preamplificazione).

Collegato l’impianto si procede a fare le misure.

Un primo tentativo puó essere quello di generare una d di Dirac mediante l’editor audio.Questo tentativo il cui risultato si puó vedere in fig. 1

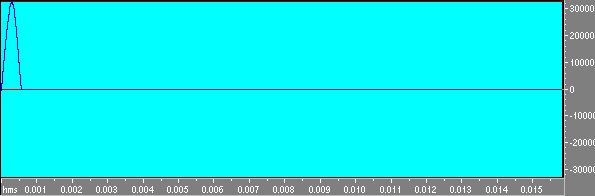
Fig 1 Il primo tentativo di generare una d visto con uno zoom sull’attacco.

si rivela peró infruttuoso ai fini pratici;l’impulso cosí generato non ha l’energia richiesta per fare una misura e quindi non si procede su questa strada.

Una seconda possibilitá é quella di generare un segnale di eccitazione con la tecnica MLS grazie ai plug-in AURORA utilizzabili nell’ambiente di Cool Edit.

Fig. 2 Segnale MLS multiplo di ordine 16 ripetuto 8 volte.

Come si puó vedere dall’analisi delle frequenze. questo segnale é molto simile al rumore bianco.

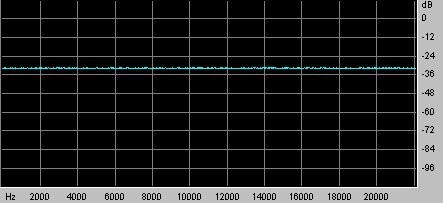
Fig 3 Spettro della MLS visto con Cool Edit

Ora si puó procedere ad una misura: in Cakewalk la prima traccia contiene il segnale MLS mentre la seconda registra simultaneamente la risposta dal microfono.

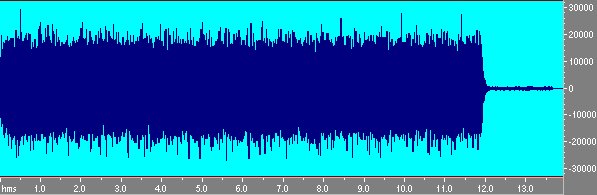
Fig. 4 Segnale di risposta registrato con il microfono.

Ora per ottenere la risposta della stanza alla d si deve deconvolvere il file di risposta con l’inverso della MLS. Per fare questo si usa la funzione deconvolve multiple MLS di AURORA. Il risultato é un’onda che rappresenta la risposta dell’ambiente alla d di Dirac.Il risultato della deconvoluzione, mostrato in figura 5, si trova nella clipboard di Windows.

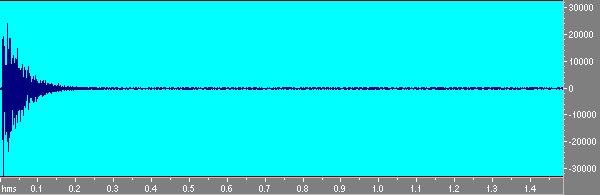
Fig 5 Risposta della stanza ottenuta con MLS.

Notiamo che nella deconvoluzione bisogna usare un filtro che rimuova la componente continua, giá integrato nel plug-in che deconvolve.

Una terza possibilitá é quella dello sweep:ovvero un segnale composto da un tono puro la cui frequenza si alza nel tempo.

In questo caso si genera sempre mediante AURORA un segnale composto da tre sweep logaritmici con frequenze che partono da 100 hz ed arrivano a 20000 hz separati da 1 secondo di silenzio ognuno.

Lo sweep usato é logaritmico (la frequenza sale nel tempo in maniera logaritmica) perché in questo modo si dá piú energia alle basse frequenze (zona critica) e si procede piú svelti sulle alte in modo da non bruciare i tweeter.In figura 6 si vede il sonogramma (rappresentazione tempo-frequenza) del segnale sweep

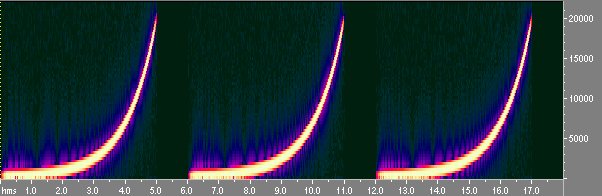
Fig 6 Sequenza di tre sweep vista con Cool Edit spectral view

Le zone piú chiare indicano maggiore energia del segnale: come si vede la variazione di frequenza é logaritmica. Si fa la misura come in precedenza e si ottiene la risposta della stanza allo sweep di fig. 7:

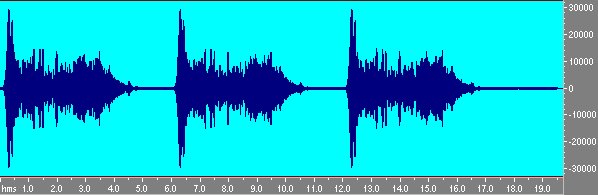
Fig 7 Risposta alla sequenza di tre sweep.

Ora bisigna convolvere con lo sweep inverso, che il plug-in di generazione dello sweep ha giá posto nella clipboard.

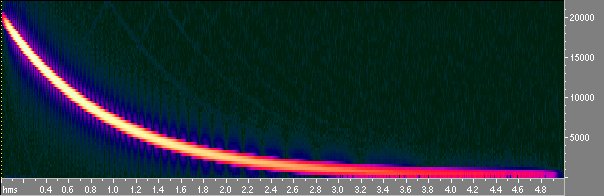
Fig 8 Sweep inverso visto con Cool Edit spectral view

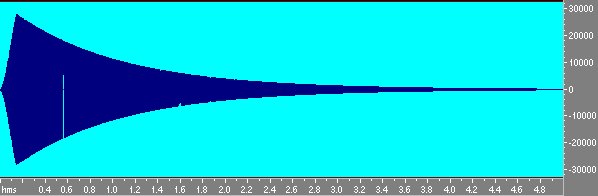
Fig 9 Sweep inverso visto come ampiezza-tempo.

Notiamo che mentre lo sweep diretto ha ampiezza costante lo sweep inverso é calante in ampiezza in modo da compensare la logaritmicitá dello sweep che dava piú energia alle basse frequenze. Infatti lo sweep logaritmico ha energia crescente di 3 db per ottava e quindi é un rumore rosa, se si convolve questo segnale con sé stesso non si ottiene la d di Dirac ma un segnale che va giú di 6 db per ottava.Questo viene compensato dal guadagno variabile dell’inverso. Convolvendo lo sweep col suo inverso si ottiene invece la d di Dirac;osservando attentamente si nota peró che non é esattamente la d ma un filtro passabanda da 100 hz a 20000 hz. Questo perché la banda passante non arriva alla frequenza di Nyquist ma si ferma a 20000.

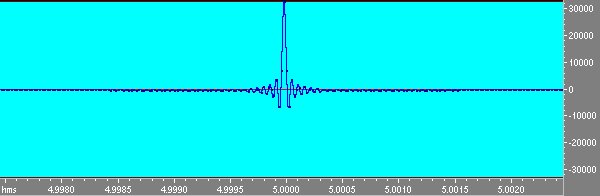
Fig 10 d ottenuta dallo sweep.

Convolvendo invece il segnale di risposta della stanza con lo sweep inverso otteniamo la risposta della stanza. Notiamo intanto che avendo tre sweep si hanno anche tre risposte che é possibile mediare fra loro ed inoltre come queste tre risposte siano assai simili a quella ottenuta con la tecnica MLS,ma molto piú pulite. In fig. 11 la risposta dell’ambiente ottenuta con lo sweep.

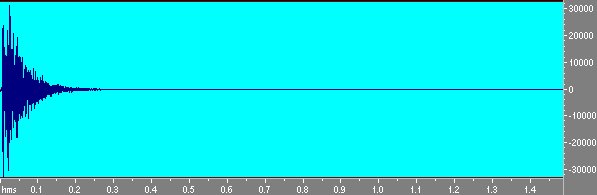
Fig 11 Risposta della stanza ottenuta da sweep e mediata.

Terminata la parte di misura si puó fare un’analisi cominciando dalla risposta ottenuta con MLS: intanto si osserva l’effetto filtrante della sala nel dominio della frequenza. In fig. 12 l’analisi in frequenza del sistema studiato, che comprende peró anche il sistema di riproduzione essendo esso non perfettamente lineare.

Fig 12 Risposta della stanza ottenuta da MLS e vista in frequenza.

Notiamo come il sistema, essendo formato da woofer molto grossi, riproduca meglio le basse e medie frequenze e cali sulle alte.

Con Spectra Lab é possibile vedere il segnale con in ordinata i db: si noti come fra picco del segnale e rumore ci sia una differenza di circa 45-50 db, non particolarmente buona per un sistema digitale.

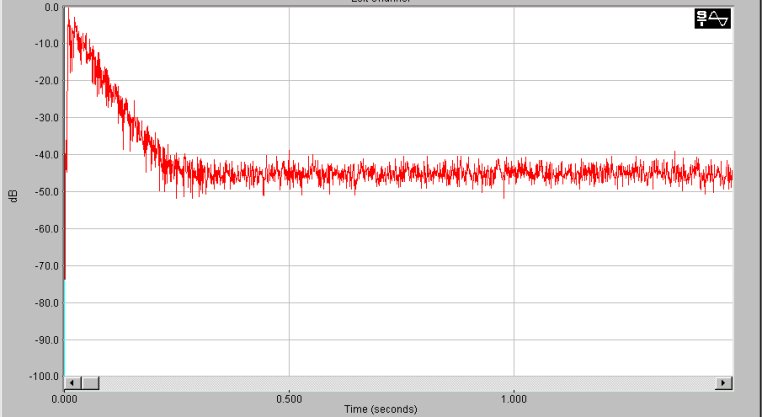
Fig 13 Risposta della stanzaottenuta da MLS vista con Spectra Lab

Bisogna peró contare che le uscite del computer sono state preamplificate da un mixer per ottenere un volume di uscita congruo con quello richiesto dall’amplificatore,questo procedimento aggiunge del rumore. Con l’integrazione di Schroeder (che Spectra Lab é in grado di fare) si puó calcolare il tempo di riverbero.

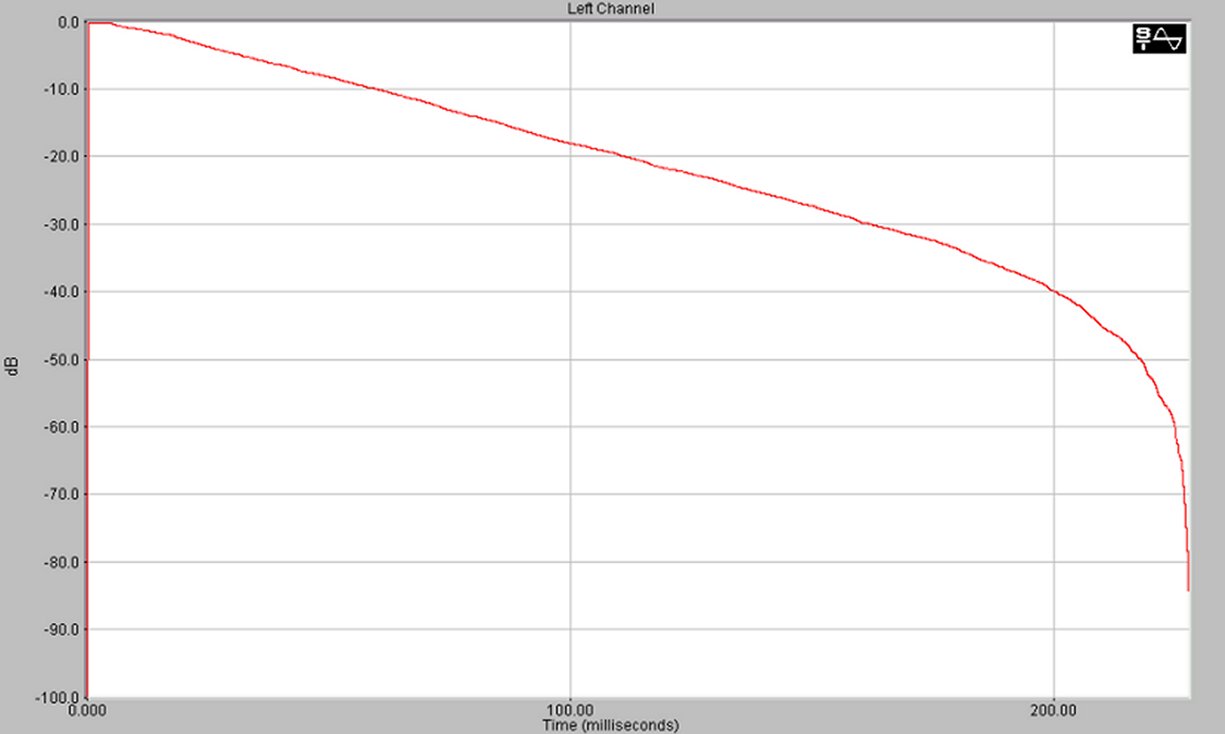
Fig. 14 Integrale di Schroeder

Siccome il picco é giá riportato a 0 db si puó vedere il tempo a cui il segnale vale -5 db e quello a cui vale –35 db sottrarre il primo al secondo e ottenere il tempo in cui il segnale ha un decadimento di 30 db.Siccome si vuole il tempo di riverbero riportato a 60 db si puó avere un risultato approssimato moltiplicando tale tempo per due.

Si ottiene quindi:

Il tempo ottenuto é congruente con i tempi tipici di stanze di piccole dimensioni.

Per fare lo stesso studio in relazione alle singole frequenze dovrei (ad esempio vedere il tempo di decadimento ad 1 Khz dovrei filtrare il segnale di risposta con un filtro passa banda) e usare lo stesso metodo di prima. Siccome avere un’analisi su tutte le frequenze sarebbe laborioso sono stati scritti dei programmi che fanno tali calcoli automaticamente fra questi uno dei moduli di AURORA tale modulo si chiama calculate acoustical parameters e calcola fra gli altri i parametri RT20 e RT30 sulle frequenze di centro banda ad ottave.

OCTAVE BAND ACOUSTICAL PARAMETERS

RTU = User(-5 dB, -15 dB)

N.B. I parametri qui calcolati sono relativi alla risposta allo sweep perché quella relativa alla MLS non dava la possibilitá di calcolare il parametro RT30 a varie frequenze.

Tale calcolo é compreso anche nel software MLSSA,che in aggiunta ha molte altre funzionalitá. Queste lo rendono ancora oggi un potente strumento nell’analisi delle sale. Si possono vedere gli spettri dei principali parametri acustici. Inoltre MLSSA consente di fare l’analisi di Fourier, di visualizzare il segnale per terzi di ottava e posso esportare i dati in formato testo,inoltre puó fare le rappresentazioni di tipo waterfall. Questo é utile perché il nostro orecchio percepisce decine di spettri diversi durante l’evolversi della nostra risposta. La possibilitá di fare tali grafici é comunque compresa anche su Spectra Lab (Fig. 15). Un altro modo di rappresentare il decadimento é la curva ETC (energy time curve).

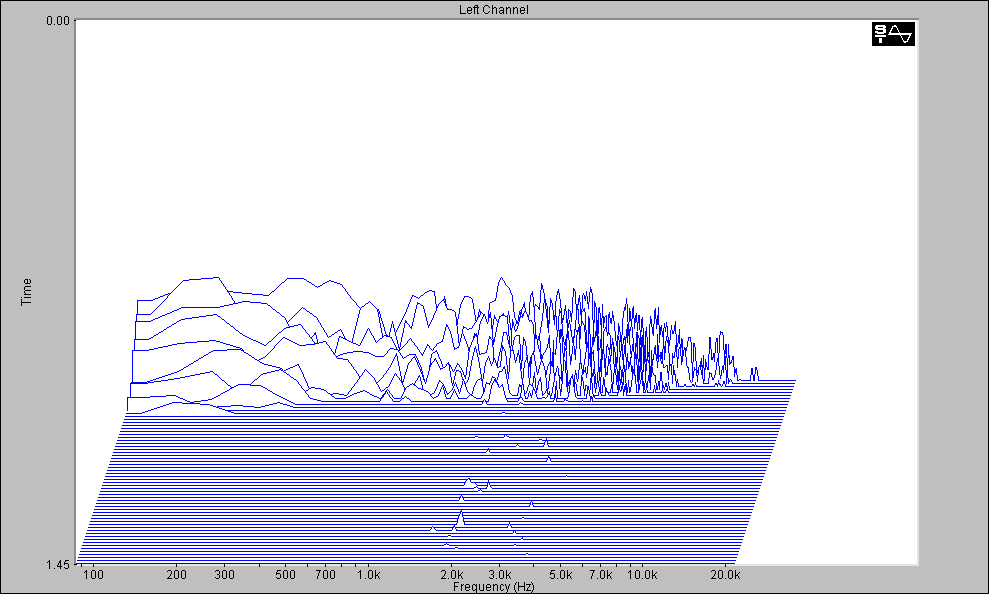
Fig.15 Risposta della stanza in 3d ottenuta da Spectra Lab

Infine esistono alcuni altri parametri utilizzati come descrittori di qualitá del campo sonoro,principalmente in riferimento all’attivitá musicale.La base concettuale di questi parametri é la misurazione della parte di suono riverberato che arriva in concomitanza con una parte dell’onda diretta integrandovisi ( considerato "utile ") a confronto con la parte che arriva dopo ( una parte piú propriamente di riverberazione che peró tende a sporcare il suono). Questo ha portato alla definizione dell’indice di chiarezza, esistente in due versioni ovvero C50 e C80 (in relazione all’ampiezza della finestra temporale che si assegna al suono utile). In particolare 50 e 80 sono i tempi espressi in millisecondi del massimo ritardo del suono utile.

 Detta p la pressione si definisce:

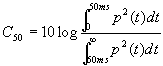[1]

Si usa il logaritmo perché questo parametro é in db. É da notare come l’energia sia espressa come quadrato della pressione anche se come si é visto é una maniera inpropria.Valori ottimali di questo indice variano fra –1 e 1 db,valori superiori a 1 db indicano un suono troppo secco, simile al suono all’aperto mentre valori inferiori a –1 indicano una eccessiva riverberazione del suono.

Il secondo indice é esattamente uguale al primo con l’unica differenza che l’intervallo di integrazione é esteso a 80 ms.

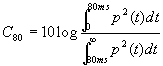[2]

Mentre il primo parametro é destinato alla valutazione di sale per il parlato il secondo é utilizzato nelle sale adibite all’ascolto di musica.Questo perché per una percezione gradevole del parlato si ha necessitá di un legame meno presente che nel caso della musica.Si definisce inoltre un indice di definizione

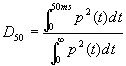[3]

Questo é un parametro similare a Ce che non aggiunge particolari informazioni allo stesso. La scelta di uno dei due dipende solo dall’abitudine del tecnico.Infine si usa il tempo baricentrico il cui pregio é la mancanza di un limite netto nell’integrazione che permette di ottenere valori piú costanti.

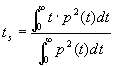[4]

Questo parametro si misura in ms ed i suoi valori ottimali sono 30-80 ms per la parola e 50-120 ms per la musica.

Esistono altri parametri molto piú avanzati che peró non vengono trattati in questo corso.

Inoltre si definiscono dei parametri spaziali. ’aspetto spaziale del suono é infatti particolarmente importante nell’ascolto della musica in quanto le buone sale da concerto inviluppano l’ascoltatore nel campo sonoro. Per fare misure relative al grado di spazialitá del suono bisogna peró fare misure con un altro tipo di microfono. In particolare si usano microfoni dotati di due capsule coincidenti, una omnidirezionale ed una a figura di otto orientata con il piano di sensibilitá parallelo alle orecchie dell’ascoltatore. Questo microfono ha due uscite indipendenti chiamate omni e figura di 8,la prima ci dá Pla seconda invece ci dá una velocitá che viene erroneamente chiamata P. Esiste una categoria di parametri basati su queste misure:

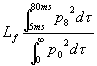[5]

Questo parametro si chiama lateral fraction ed é una percentuale. Un altro parametro simile é l’efficenza laterale

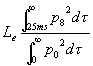[6]

Questi parametri sono definiti dalla norma ISO 3382/97.

Un ultimo parametro derivante dal giappone é lo IACC (inter aural cross correlation).Infatti secondo la metodica giapponese le misure vanno effettuate con microfoni binaurali ovvero microfoni stereo simili alle cuffie di ascolto e quindi indossati sulla testa e sovrapposti alle orecchie. In particolare si possono fare misure con un microfono di questo tipo e un registratore (ad esempio un DAT). Grazie a queste tecniche si puó ricostruire il suono di un ambiente convolvendo la sua risposta con una registrazione anecoica (priva di qualsiasi effetto dovuto alla riflessione del suono). Proviamo quindi ad auralizzare un segnale anecoico con la risposta della stanza studiata.

Fig. 16 Segnale anecoico

E con il comando convolve with clipboard lo si auralizza.

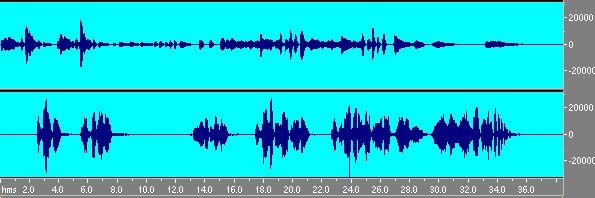
Fig. 17 Il segnale di fig. 16 auralizzato con le cartatteristiche della stanza misurate precedentemente.