Sfruttando l'equazione di Clausius per un ciclo reversibile

possiamo definire una nuova funzione di stato chiamata entropia che viene definita in modo differenziale

Per dimostrare che l'entropia è funzione di stato consideriamo, come in figura 1, tre diverse trasformazioni reversibili di cui due aventi lo stesso orientamento e la terza con orientamento opposto.

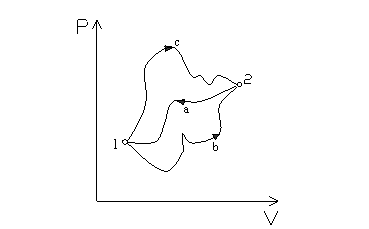
Fig.1

Consideriamo il ciclo reversibile chiuso c-a, per l'equazione di Clausius si può scrivere

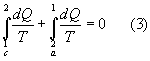
da cui si ricava facilmente

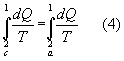
Analogamente si può procedere lungo il ciclo reversibile chiuso c-b scrivendo,sempre per Clausius

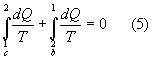
quindi

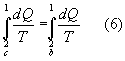
da cui si ricava immediatamente

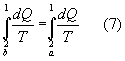
Per l'arbitrarietà dei cammini reversibili a e b scelti si può subito dedurre che l'integrale

non dipende dal percorso seguito ma solo dagli estremi di integrazione 1 e 2, fatto che dimostra come l’entropia sia una funzione di stato e per cui possiamo scrivere in forma finita

dove S indica l'entropia.

Derivando si ritrova facilmente l'equazione differenziale (1) con cui era stata definita prima l'entropia.

Pochè è possibile solo determinare una differenza di entropia o una sua forma differenziale è facile dedurre che questa nuova grandezza viene definita a meno di una costane S₀ , che abitualmente viene posta uguale a 0.

L'unità di misura di questa nuova grandezza di stato è facilmente ricavabile dall'equazione differenziale e si ottiene subito

Studiamo ora le trasformazioni reversibili che avvengono senza scambio di calore con l'ambiente esterno, in esse si ha

da cui

Queste trasformazioni si chiamano adiabatiche e avvengono senza variazione di entropia, calcoliamo l'equazione di una tale trasformazione reversibile.

Per un gas perfetto si ha

e anche

Poiché dQ = 0 si ha

e anche

da cui dividendo la seconda equazione per la prima

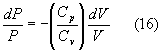
che integrando dà:

essendo g = C_p / C_v .

Passando alla forma esponenziale

Essendo g maggiore di 1 si ha che la pendenza della curva che rappresenta una trasformazione adiabatica reversibile, su di un grafico P-V, è maggiore di quella della curva che rappresenti una trasformazione isoterma come si può vedere dal grafico in figura 2.

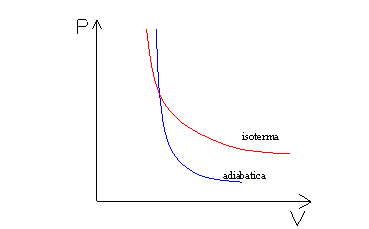
Fig.2

Essendo l'entropia una funzione di stato si possono avere trasformazioni isoentropiche, come tutte le trasformazioni reversibili adiabatiche, che non sono però adiabatiche e tanto meno reversibili , come è mostrato in figura 3, dove, avendo gli estremi su una curva adiabatica, anche la trasformazione irreversibile risulta isoentropica.

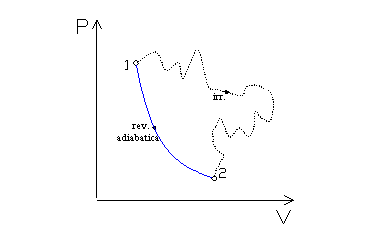
Fig. 3

Questa trasformazione irreversibile non genera alcuna variazione di entropia nel sistema ma non è detto che non faccia cambiare l'entropia dell'universo.

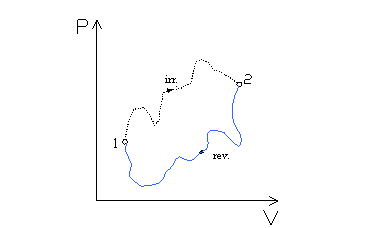
Fig. 4

Se si considerano due trasformazioni aventi gli stessi estremi però con cammini diversi, di cui una reversibile e una irreversibile, ma internamente invertibile, come mostrato in figura 4, si può scrivere la disuguaglianza di Clausius.

da cui essendo una delle due trasformazioni irreversibile

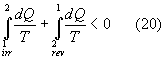
da cui

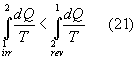
Quindi, utilizzando la precedente formula (8)

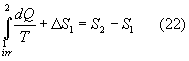
dove DS₁ viene normalmente chiamato "salto entropico" o "produzione entropica", nonostante sia un'espressione impropria per indicare la quantità mancante di entropia per soddisfare l'eguaglianza.

Si può affermare quindi che "l'entropia dell'universo aumenta", infatti si può scrivere, per qualsiasi trasformazione termodinamica

che esprime in forma matematica il "Principio di non diminuzione dell'entropia".

Studiamo ora cosa succede quando si viola il secondo principio in termini entropici: in figura 5 è mostrata una macchina che produce lavoro prelevando calore da un unico serbatoio a temperatura costante, questo viola evidentemente l'enunciato di Kelvin-Planck.

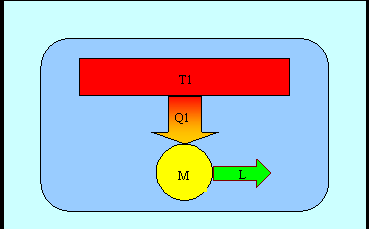
Fig. 5

La macchina è una macchina termica ideale che lavora ciclicamente effettuando solo trasformazioni reversibili, essa dopo ogni ciclo tornerà nello stato termodinamico iniziale non generando alcuna variazione dell'entropia

mentre per la sorgente di calore si ha

essendo

si ha

Ciò è in evidente contraddizione con il principio di non diminuzione dell'entropia.

Studiamo analogamente cosa succede se si viola l’enunciato di Clausius.

Consideriamo quindi un sistema che trasferisca calore da un sorgente a temperatura T₂ ad uno a temperatura superiore T₁ , come mostrati in figura 6.

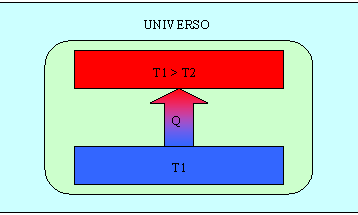
Fig. 6

Calcoliamo le variazioni d’entropia dei singoli serbatoi per ricavare la variazione di entropia dell’universo.

da cui facilmente si ricava

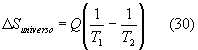
La variazione di entropia dell’inverso risulta così essere minore di zero, essendo T₁ maggiore di T₂ , e ciò è in netta contraddizione con il principio di non diminuzione dell’entropia.

Consideriamo una macchina semplice, che lavori in modo ciclico e che effettui solo processi termodinamici reversibili, che prelevi calore da una sorgente di calore a temperatura T₁ rendendo parte di questo ad una sorgente a temperatura inferiore T₂ , producendo così lavoro, come mostrato in figura 1.

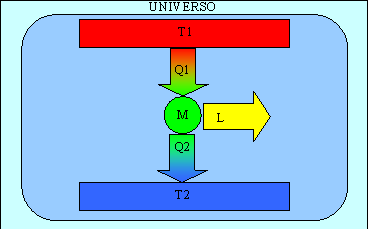
Fig. 1

Sotto queste ipotesi la macchina lavora senza causare variazioni dell’entropia dell’universo: calcoliamo le variazioni di entropia di ogni singolo componente

e uguagliamone la somma alla variazione di entropia dell’universo.

Si ricava immediatamente

Questa macchina può effettuare solo processi isotermici o adiabatici e viene chiamata macchina di Carnot.

Se rappresentiamo un ciclo di tale macchina su un grafico P-V otteniamo il disegno di figura 2, che viene chiamato ciclo di Carnot.

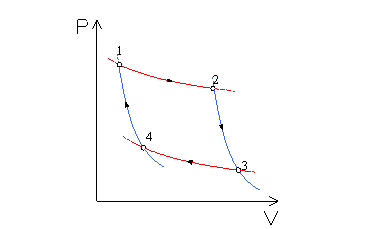
Fig. 2

Come si può vedere dal grafico i processi effettuati da tale macchina sono:

• da 1 a 2 isotermico,
• da 2 a 3 adiabatico,
• da 3 a 4 isotermico,
• da 4 a 1 adiabatico.

Come di tutte le macchine viene definito un "coefficiente di rendimento" chiamato coefficiente economico, che non è altro che il rapporto fra il lavoro L prodotto e l’energia acquisita per produrlo:

ma poiché nella macchina di Carnot il rapporto fra la quantità di calore Q₂ e quella Q₁ è uguale al rapporto fra la temperatura T₂ e la temperatura T₁ , si ottiene facilmente

da cui si nota facilmente che l’unica cosa da cui dipende la macchina di Carnot sono le temperature a cui la si fa lavorare e non cambia nulla se due macchine ideali lavorano fra le stesse temperature ma con differenti processi.

Il coefficiente economico dell macchina di Carnot rappresenta, in un certo senso, il limite massimo di resa che può avere una macchine termica che lavori fra determinate temperature; infatti, se ipotizziamo di avere una macchina che abbia un e maggiore di e_c , in questo caso si avrebbe che il lavoro prodotto sarebbe

essendo

Se scomponiamo il lavoro L in due parti avremo che una delle due può essere utilizzata in una seconda macchina per portare una quantità di calore, pari a quella prelevata dalla prima macchina , nel serbatoio a temperatura maggiore T₁ , come mostrato in figura 3.

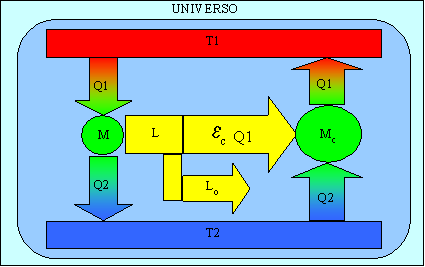
Fig. 3

Si avrebbe quindi che la prima macchina avrebbe generato lavoro prelevando calore da una sola sorgente a temperatura costante, in contraddizione con il secondo principio della termodinamica.

Consideriamo, come esempio, una centrale che produce energia elettrica bruciando combustibile fossile e lavorando fra le temperature di 1800 ^o K e 300 ^o K , il coefficiente economico di una macchina di Carnot che lavori fra le stesse temperature è

che non è assolutamente una cifra realistica .

In genere le macchine reali hanno un coefficiente molto inferiore a e_c poiché vi sono dei processi irreversibili come è mostrato in figura 4 che è un più realistico schema di funzionamento di una macchina.

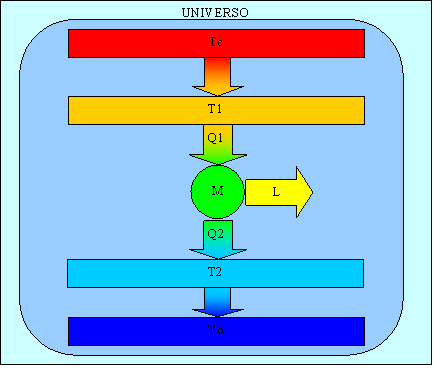
Fig. 4

Dal disegno si nota come vi siano processi irreversibili che causano :

• abbassamento di T₁,
• innalzamento di T₂,
• perdita conseguente di lavoro prodotto.

Come abbiamo accennato prima se vi sono delle trasformazioni che rendono esternamente irreversibile il processo allora vi è perdita di lavoro.

Studiamo una situazione come quella di figura 1 per determinare l’entità di una tale perdita.

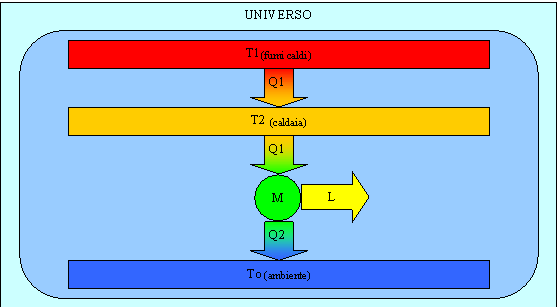Fig. 1

In queste condizioni si ha che il primo flusso di calore, dai fumi alla caldaia, essendo un processo irreversibile causa un’irreversibilità esterna del sistema con conseguente aumento di entropia dell’universo.

Calcoliamo ora sia il lavoro L prodotto reversibilmente dalla macchina termica, sia il lavoro L’ prodotto dall’intero sistema.

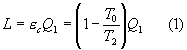
da cui si può calcolare la perdita di lavoro DL

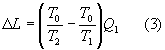
Calcoliamo ora la variazione di entropia di ogni singolo componente per ricavare la produzione entropica del sistema, tenendo conto che la variazione di entropia della macchina è nulla in quanto essa è ciclica.

da cui si ricava, sostituendo il valore precedentemente ricavato di L, sommando le singole variazioni la variazione di entropia dell’universo

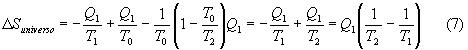
ottenendo definitivamente

da cui si nota subito la correlazione fra grado di irreversibilità, dato dalla produzione entropica, e perdita di lavoro.

Con i termini di anergia ed exergia si vuole specificare ulteriormente il concetto di energia, infatti si ha:

• Exergia : parte di energia che può essere completamente trasformata in lavoro,
• Anergia : parte di energia che viene persa nel processo di trasformazione da energia a lavoro,

come mostrato nelle figura 1 .

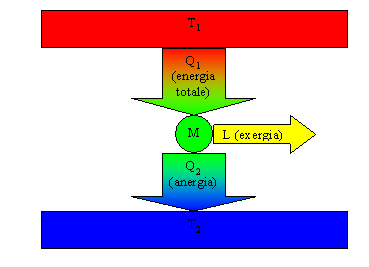
Fig. 1

Partendo da questa distinzione si tende a dividere intuitivamente l’energia in due "forme", una più nobile e l’altra meno: energia "nobile" può essere l’energia elettrica, potenziale e tutte quella forme che hanno un alto contenuto exergetico, il calore è considerata un forma di energia poco nobile in quanto ha mediamente un basso contenuto exergetico e un discreto contenuto di anergia.

Ora non bisogna considerare l’anergia come una parte inutile dell’energia poiché essa può essere usata per altri scopi.

Si consideri, per esempio, il calore di scarto di una centrale elettrica, esso può venir usato per il teleriscaldamento come viene fatto ormai da anni nella città di Brescia, con un notevole risparmio di risorse energetiche a livello cittadino.