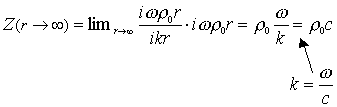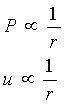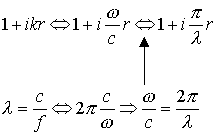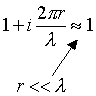Universita` degli studi di Parma
Corso di Laurea in Ingegneria Elettronica, Informatica delle Telecomunicazioni
Anno Accademico 1999/2000
Corso di Fisica Tecnica
Docente: Prof. Angelo Farina
Autori: Bertoli Samuele Mtr. 110549
Ciuffardi Gianni Mtr. 113831
Lezione del 30/11/99
Ore: 14.30-16.30
Argomenti Trattati: Onde sferiche
Potenziale di Velocita`
Velocita`
Pressione
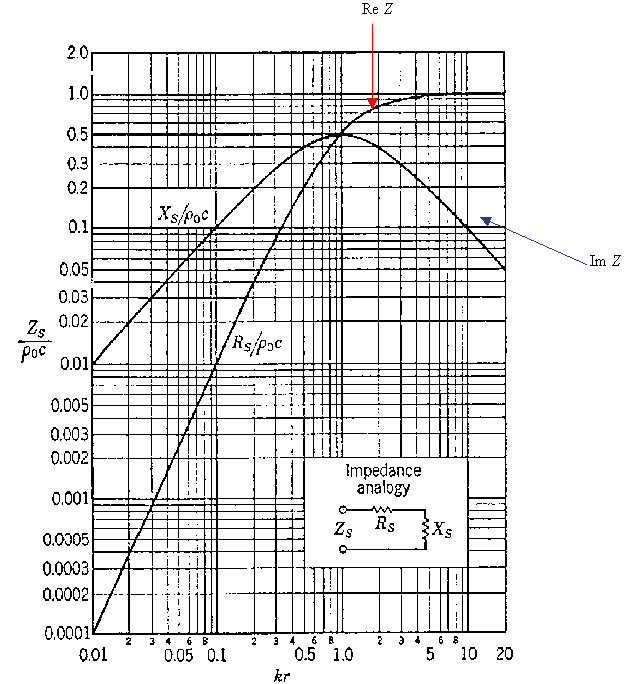
Impedenza
Intensita`del Campo
Appendice a) Coordinate Sferiche
Appendice b) Coordinate Cilindriche
Appendice c) Gradiente e Laplaciano in funz. Coordinate
Onde Sferiche
Sia S una Sorgente sonora costituita da una piccola sfera di centro O e di raggio R pulsante radialmente con moto periodico: dalla superficie della sfera partono delle onde longitudinali che si propagano nel mezzo circostante. Per ragioni di simmetria la velocità di propagazione è la stessa in tutte le direzioni uscenti da O, così che ogni punto equidistante da O è nello stesso stato di vibrazione: ovvero si hanno delle onde sferiche longitudinali.
Consideriamo quindi l’equazione di D’Alambert espressa in coordinate sferiche: ci poniamo in condizioni di simmetria sferica perché il campo sonoro da noi considerato presenta tale simmetria.
Equazione di D’Alambert
![]()
Dove
j potenziale di velocità
c velocità del suono
r distanza dal centro O della sorgente sonora
Definiamo quindi una nuova variabile y tale che
![]()
Sostituendo (2) nell’equazione (1) si ottiene
![]()
La soluzione di questa equazione differenziale è data da
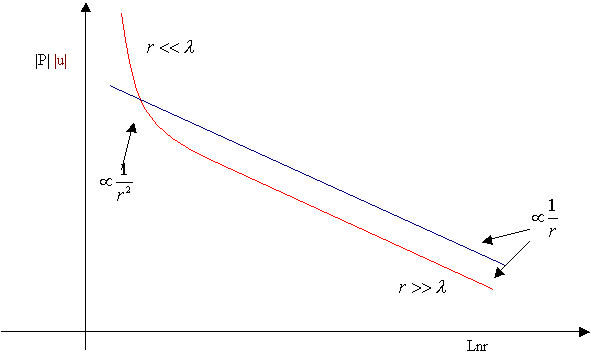
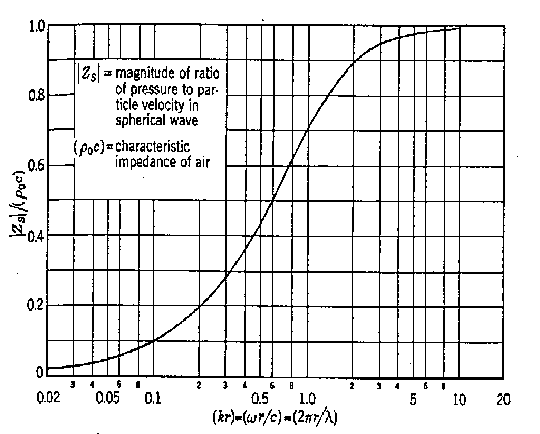
Figura 1.
Andamento qualitativo di pressione e velocità in funzione di r
Sapendo che
![]()
Si ha
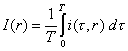
Da cui
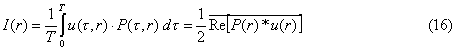
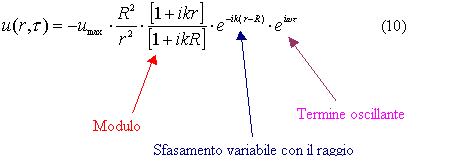
Sostituiamo in (16) le espressioni generali della pressione e della velocita` (in funzione di PMAX). Ricordiamo infatti che:
![]()
![]()
Sostituendo (17) e (18) in (16) si ottiene:
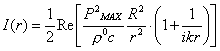
Considerando solo la parte reale si ha:

Espressione valida sia per un campo sonoro vicino alla sorgente che per uno lontano
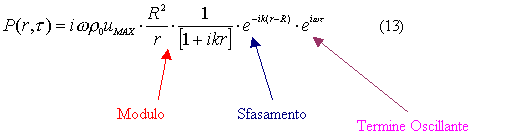
Analogamente si puo` fare per l`intensita` in funzione di uMAX , si ricava:

Rapportiamo quindi l`intensita` dell`onda sferica con quello dell`onda piana, che ricordiamo essere:
![]()
![]()
Definiamo h Efficienza di Radiazione e osserviamo che:
![]()
![]()
Quindi l`efficienza di radiazione diventa pari a quella di un pistone infinito allorche` il raggio R della nostra sorgente sonora S e` molto grande, ossia R >> l .
Il campo sonoro prodotto da un
autoparlante e` proporzionale alla velocita` con cui il diaframma dello stesso
si sta muovendo. Definiamo percui una nuova grandezza: la Velocita` di Volume:
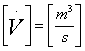 .
.
![]()
Appendice a)
Coordinate Sferiche rispetto al polo(0,0,0)
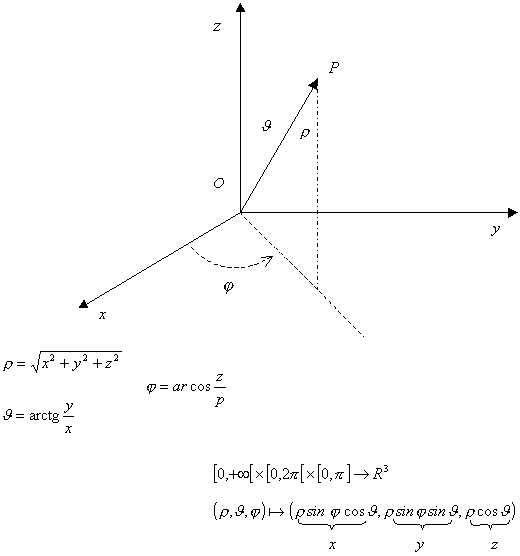
-r distanza radiale
-J colatitudine
-j azimut o longitudine
![]()
![]()
![]()
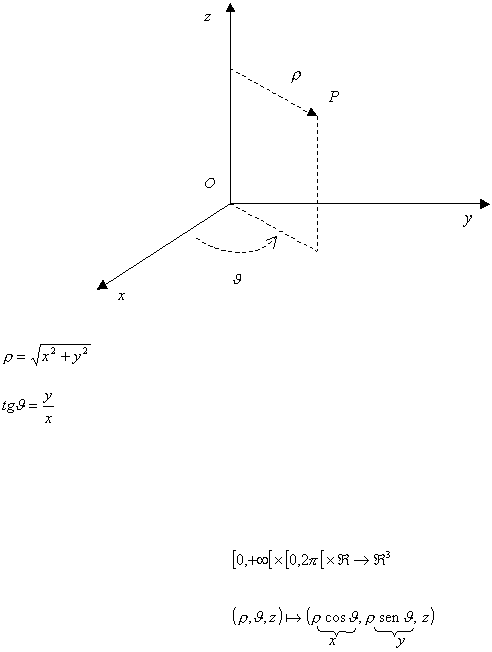
Appendice b)
Coordinate Cilindriche
Appendice c)
Vogliamo osservare come varino l`operatore gradiente e l`operatore Laplaciano in funzione del tipo di coordinate.
Sia:
![]()
Coordinate Cartesiane:
![]()
![]()
Coordinate Sferiche:
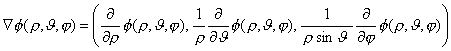
![]()
Coordinate Cilindriche:
![]()
![]()