Università degli studi di Parma
Facoltà di Ingegneria Informatica
Corso di FISICA TECNICA
Docente: Angelo Farina
Anno Accademico 1999/2000
Martedì 2/11/99 - lezione 16.30-18.30
Trascritta da Barigazzi Maddalena e Bertolazzi Rosa
Lezione riguardante la sezione del corso relativa alla termodinamica
MISCELE DI ARIA E VAPORE ACQUEO
Argomenti trattati:
Generalità
In questa lezione saranno analizzate le proprietà delle miscele di aria e acqua.
L’aria sarà considerata come un solo componente, perché la composizione dell’aria sarà assunta costante. La composizione di dettaglio in volume dell’aria secca è:
78% Azoto
21% Ossigeno
1% Gas rari (tra cui elio, neon, argon) e una piccolissima percentuale di Anidride Carbonica. All’aria aperta la percentuale di CO2 è circa 0.03%, quindi si può considerare quasi assente. Nell’aria espirata CO2 aumenta fino ad arrivare a qualche unità a seconda del tempo trascorso nei polmoni. Quindi in un’aula in cui sono presenti un centinaio di persone la percentuale di anidride carbonica non è più trascurabile; essa aumenta raggiungendo un valore costante, bilanciato dal ricambio d’aria.
L’acqua potrà essere in parte liquida ed in parete vapore.
La fase gassosa della miscela sarà considerata una miscela di due gas ideali: aria e vapore acqueo infatti il vapore presenta una pressione parziale molto piccola, quindi è lecito trascurare il comportamento da vapore surriscaldato. La composizione della fase gassosa potrà variare, per effetto di evaporazione o condensazione di acqua.
Quindi la massa di aria secca viene considerata costante (perché l’aria non si crea ne si distrugge a parte casi rari: ad esempio reazioni chimiche) mentre la massa di vapore cambia facilmente. Questo fatto spiega perché le grandezze specifiche non vengono riferite all’unità di massa della miscela, ma all’unità di massa dell’aria secca (si mantiene questa convenzione anche per compatibilità con il passato e per comodità). Ad esempio si parla di entalpia specifica definita come:
![]()
![]() ove Maria = massa dell’aria secca.
ove Maria = massa dell’aria secca.
Saturazione dell’aria e titolo
Consideriamo il seguente esperimento: in presenza di aria inizialmente secca poniamo su una bilancia un recipiente contenente acqua mantenendo pressione P e temperatura T costanti.
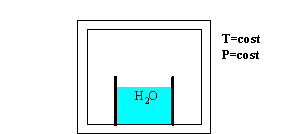
Fig. 1
Dopo un certo periodo di tempo il livello di acqua nel contenitore sarà calato, cioè una certa massa di H2O sarà evaporata nell’aria , e il livello continuerà a calare sempre più lentamente fino a rimanere costante (quindi la bilancia misurerà una diminuzione della massa di acqua)
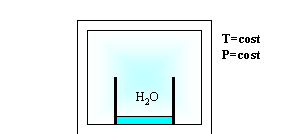
Fig. 2
Questa esperienza mostra che se si mettono a contatto aria e acqua liquida , a temperatura e pressione costanti , l’acqua evapora fino a che la pressione parziale del vapore saturo eguaglia la pressione di saturazione dell’acqua alla temperatura T alla quale si opera.
In altri termini la presenza d’acqua non influisce sulla quantità di acqua che si volatilizza , ma soltanto sulla velocità del processo.
A questo punto possiamo introdurre una nuova grandezza : il titolo, definito come
![]() ( 1 )
( 1 )
ove Mvap = massa di acqua evaporata
Maria= massa di aria secca
Kgvap = chilogrammi di vapore
Kgaria = chilogrammi di aria
Il titolo è il rapporto tra pesi di sostanze chimiche diverse , non si tratta di un numero puro! Quindi non va confuso con il titolo di vapore saturo che invece è un numero puro. Inoltre il titolo x non è confinato ad essere minore di 1 (ricordiamo che per il titolo di vapore saturo vale xvapore saturo < 1).
Di solito per evitare semplificazioni dell’unità di misura, il titolo viene espresso in gvap /kg aria.
La grandezza che esprime quale è la massima massa di acqua che può volatilizzarsi in una massa di aria secca è il titolo di saturazione, cioè il titolo calcolato in condizioni di equilibrio tra aria e acqua in presenza di acqua liquida (in riferimento all’esperimento visto, il titolo calcolato quando il livello dell’acqua resta costante).
Il titolo di saturazione xsat è dipendente da temperatura e pressione
xsat = xsat (p,t), ad esempio cresce al crescere della temperatura, quindi quando si parla di titolo di saturazione si considerano fissati i valori di questa due grandezze.
Solitamente si lavora in un sistema isobaro , a pressione atmosferica patm=1,013 bar quindi la dipendenza viene ad essere dalla sola temperatura.
I valori del titolo di saturazione riferiti alla pressione atmosferica in funzione della temperatura sono reperibili su apposite tabelle.
Tabella 1
Tabella dei valori assunti da alcuni parametri termodinamici della miscela aria-vapore acqueo per j = 1 e P = 1.013 bar
|
Temperatura dell’aria T °C |
Pressione di vapore dell’aria satura P mbar P mmHg
|
Titolo di saturazione x g/Kg |
|
|
-20 |
1.02 |
0.756 |
0.63 |
|
-19 |
1.13 |
0.848 |
0.7 |
|
-18 |
1.25 |
0.938 |
0.77 |
|
-17 |
1.37 |
1.028 |
0.85 |
|
-16 |
1.5 |
1.125 |
0.93 |
|
-15 |
1.65 |
1.238 |
1.01 |
|
-14 |
1.81 |
1.358 |
1.11 |
|
-13 |
1.98 |
1.485 |
1.22 |
|
-12 |
2.17 |
1.628 |
1.34 |
|
-11 |
2.37 |
1.778 |
1.46 |
|
-10 |
2.59 |
1.943 |
1.6 |
|
-9 |
2.83 |
2.123 |
1.75 |
|
-8 |
3.09 |
2.318 |
1.91 |
|
-7 |
3.36 |
2.520 |
2.08 |
|
-6 |
3.67 |
2.753 |
2.27 |
|
-5 |
4 |
3 |
2.49 |
|
-4 |
4.36 |
3.270 |
2.69 |
|
-3 |
4.75 |
3.563 |
2.94 |
|
-2 |
5.16 |
3.870 |
3.19 |
|
-1 |
5.61 |
4.208 |
3.47 |
|
0 |
6.09 |
4.568 |
3.78 |
|
1 |
6.56 |
4.920 |
4.07 |
|
2 |
7.04 |
5.280 |
4.37 |
|
3 |
7.57 |
5.678 |
4.7 |
|
4 |
8.11 |
6.083 |
5.03 |
|
5 |
8.7 |
6.526 |
5.4 |
|
6 |
9.32 |
6.991 |
5.79 |
|
7 |
9.99 |
7.493 |
6.21 |
|
8 |
10.7 |
8.026 |
6.65 |
|
9 |
11.46 |
8.596 |
7.13 |
|
10 |
12.25 |
9.188 |
7.63 |
|
11 |
13.09 |
9.818 |
8.15 |
|
12 |
13.99 |
10.493 |
8.75 |
|
13 |
14.94 |
11.206 |
9.35 |
|
14 |
15.95 |
11.963 |
9.97 |
|
15 |
17.01 |
12.759 |
10.6 |
|
16 |
18.13 |
13.599 |
11.4 |
|
17 |
19.32 |
14.491 |
12.2 |
|
18 |
20.59 |
15.444 |
12.9 |
|
19 |
21.92 |
16.441 |
13.8 |
|
20 |
23.31 |
17.484 |
14.7 |
|
21 |
24.8 |
18.602 |
15.6 |
|
22 |
26.37 |
19.779 |
16.6 |
|
23 |
28.02 |
21.017 |
17.7 |
|
24 |
29.77 |
22.3 |
18.8 |
|
25 |
31.6 |
23.702 |
20 |
|
26 |
33.53 |
25.150 |
21.4 |
|
27 |
35.56 |
26.672 |
22.6 |
|
28 |
37.71 |
28.285 |
24 |
|
29 |
39.95 |
29.965 |
25.6 |
|
30 |
42.32 |
31.748 |
27.2 |
|
31 |
44.82 |
33.618 |
28.8 |
|
32 |
47.46 |
35.575 |
30.6 |
|
33 |
50.18 |
37.638 |
32.5 |
|
34 |
53.07 |
39.806 |
34.4 |
|
35 |
56.1 |
42.078 |
36.6 |
|
36 |
59.26 |
44.449 |
38.8 |
|
37 |
62.6 |
46.954 |
41.1 |
|
38 |
66.09 |
49.572 |
43.5 |
|
39 |
69.75 |
51.317 |
46 |
|
40 |
73.58 |
55.198 |
48.8 |
|
41 |
77.59 |
58.197 |
51.7 |
|
42 |
81.8 |
61.355 |
54.8 |
|
43 |
86.18 |
64.64 |
58 |
|
44 |
90.79 |
68.098 |
61.3 |
|
45 |
95.6 |
71.706 |
65 |
|
46 |
100.61 |
75.464 |
68.9 |
|
47 |
105.87 |
79.409 |
72.8 |
|
48 |
111.33 |
83.504 |
77 |
|
49 |
117.07 |
87.81 |
81.5 |
|
50 |
123.04 |
92.288 |
86.2 |
|
55 |
150.94 |
117.715 |
114 |
|
60 |
198.7 |
149.037 |
152 |
|
65 |
249.38 |
187.05 |
204 |
|
70 |
310.82 |
233.134 |
276 |
|
75 |
384.5 |
288.398 |
382 |
|
80 |
472.28 |
354.239 |
545 |
|
85 |
576.69 |
432.553 |
828 |
|
90 |
699.31 |
524.525 |
1400 |
|
95 |
834.09 |
625.618 |
3120 |
|
100 |
1013 |
759.812 |
- |
Il titolo di saturazione non dipende dalla presenza dell’aria , ma esclusivamente dal vapore. Nell’esperimento precedentemente visto la massa di acqua evaporata sarebbe stata la medesima anche in assenza di aria (nel vuoto) in quanto , per ipotesi di gas perfetto, il vapore si espande come se l’aria non ci fosse . L’unica differenza è data dalla velocità di vaporizzazione in quanto la presenza dell’aria rallenta il raggiungimento dell’equilibrio.
Il concetto che sia l’aria a saturarsi è sbagliato !
In realtà è l’acqua che si satura.
Vediamo ora come interpretare titolo e titolo di saturazione attraverso due esempi .
Una massa di aria umida , la nuvola , che si trova alla temperatura TA e pressione P ha inizialmente un titolo x minore di quello di saturazione xsat A
( relativo alla temperatura TA ).
Se si verifica un calo della temperatura il titolo di saturazione xsat risulta inferiore rispetto a prima . Quindi può verificarsi che il titolo della massa d’aria umida sia minore del nuovo titolo di saturazione. In sostanza la nuvola contiene più acqua di quanta ne possa contenere e si verifica il fenomeno della pioggia.

Fig. 3

Fig.4
2) Normalmente il vapore acqueo è trasparente, quindi non visibile nell’aria , ma in condizioni prossime a quelle del titolo di saturazione si verifica il fenomeno della nebbia. La nebbia è una situazione molto stabile , anche se sembrerebbe non esserlo, che tende ad automantenersi grazie al comportamento da termostato dell’acqua. Supponiamo infatti che la temperatura scenda di qualche grado: l’acqua condensa e cede all’ambiente il calore di vaporizzazione. Questa energia liberata tenderà a riportare il sistema all’equilibrio.
Vista dal satellite la Terra risulta per 3/4 coperta da nebbia , ma se sul nostro pianeta ci fosse qualche miliardo di metri cubi di acqua in più il titolo dell’atmosfera aumenterebbe sino ad arrivare a cavallo del titolo di saturazione e la Terra sarebbe ricoperta dalla nebbia perenne (come lo sono molti pianeti).
Grado igrometrico
Il titolo x è un numero piccolo e preso a se stante non ci da una indicazione diretta del livello di saturazione del vapore acqueo nella miscela : per capire se l’aria sia secca o satura è necessario confrontare il titolo con quello di saturazione . Quindi si rende opportuno introdurre una nuova grandezza: il grado igrometrico , definito come :
![]() ( 2 )
( 2 )
ove r v = massa del vapore acqueo contenuto nell’unità di volume della fase gassosa
r vsat= masa del vapore acqueo che sarebbe contenuto nell’unità di volume della fase gassosa in condizioni di saturazione (cioè in equilibrio con in liquido)
Piochè per un gas ideale , a temperatura fissata , la densità è proporzionale alla pressione si ha anche , equivalentemente:
![]() ( 3 )
( 3 )
ove Pv = pressione parziale di vapore acqueo nella miscela
Pv Sat = pressione di vapore saturo secco
(fissata la temperatura T della miscela)
Il grado igrometrico può assumere valori compresi tra 0 e 1 , oppure in modo equivalente può essere espresso in percentuale ; in tal caso prende il nome di umidità relativa .
Per capire meglio cosa sia in pratica il grado igrometrico affidiamoci a questo esempio:
Consideriamo una massa d’aria umida alla temperatura T = 20°C. La pressione di saturazione ad una tale temperatura è Psat = 23.31 mbar (questo valore è stato ricavato dalla Tabella 1) e la pressione parziale del vapore contenuto nella miscela è Pv = 16.317 mbar.
Il grado igrometrico si ricava dalla ( 3 ) sostituendo i valori numerici forniti:
![]() o equivalentemente Umidità relativa = 70%
o equivalentemente Umidità relativa = 70%
Questo significa che la miscela contiene il 70% della quantità di vapore che la renderebbe satura.
Quindi il grado igrometrico j ci da una misura immediata di quanto l’aria sia effettivamente prossima alla saturazione.
Relazione tra titolo e grado igrometrico
Consideriamo una miscela di aria e vapore acqueo , in assenza di liquido. Noto il grado igrometrico j vogliamo ricavare il titolo x relativo alla miscela.
Per le ipotesi precedentemente fatte , è lecito considerare aria e vapore acqueo0 come due gas ideali. Quindi possiamo scrivere l’equazione di stato dei gas perfetti separatamente per la massa d’aria e la massa di vapore acqueo, considerando come volume a disposizione delle singole massa il volume totale. (questa assunzione discende dalla Legge di Dalton sulle miscele dei gas perfetti)
Quindi
Aria ![]() ( 4 )
( 4 )
Vapore acqueo ![]() ( 5 )
( 5 )
Essendo valide le seguenti relazioni
![]() ( 6 )
( 6 )
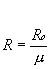 ( 7 )
( 7 )
ove M = massa del gas
n = numero di moli del gas
m = massa molare del gas
si ottiene:
Aria ![]() ( 8 )
( 8 )
Vapore acqueo ![]() ( 9 )
( 9 )
Dividendo membro a membro la ( 8 ) e la ( 9 ) otteniamo:
![]() Þ
Þ
![]() ( 10 )
( 10 )
Ricordiamo che per definizione di titolo
![]() ( 1 )
( 1 )
Quindi per la ( 6 ) e la ( 10 ) si ha :
![]() ( 11 )
( 11 )
I valori delle masse molari di aria e vapore d’acqua sono rispettivamente :
m = 29 kg/mol e m = 18 kg/mol.
Sostituendoli nella ( 11 ) arriviamo alla
![]() ( 12 )
( 12 )
Questa relazione ci permette di calcolare il titolo a partire dalle pressioni parziali di vapore e aria secca.
Dalla definizione di grado igrometrico ( 3 ) si ricava:
![]() ( 13 )
( 13 )
Sostituendo la (13 ) nella ( 12 ) si ottiene:
![]() ( 14 )
( 14 )
Dovendo inoltre valere che
![]() ( 15 )
( 15 )
ove PTOT = pressione totale della miscela (di solito nota e pari a 1 bar)
Si arriva alla formula che esprime la relazione cercata tra titolo x e grado igrometrico j :
![]() ( 16 )
( 16 )
Calore specifico medio a pressione costante
Definiamo il calore specifico della miscela cp’ come la media pesata dei calori specefici dei componenti riferita alla massa di aria secca:
![]() ( 17 )
( 17 )
ove x = titolo della miscela
cparia = calore specifico dell’aria a pressione costante
cpvap = calore specifico del vapore acqueo a pressione costante
Questo risultato si ottiene dalla formula valida per le miscele dei gas perfetti:
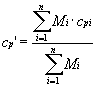 ( 18 )
( 18 )
ove cpi = calore specifico dell’i-esimo componente della miscela
Mi = massa dell’i-esimo componente della miscela
Dalla ( 18 ) il calore specifico medio cp’ si ricava come la media pesata dei calori specifici dei singoli componenti riferita alla massa totale della miscela .
Noi invece vogliamo riferire il calore specifico alla sola massa dell’aria secca M .
Quindi
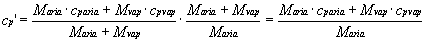 (19)
(19)
ed essendo
![]() ( 1 )
( 1 )
si ottiene la ( 17 ).
Entalpia specifica j in assenza di liquido
L’entalpia è una proprietà estensiva. Pertanto ,l’entalpia specifica j .cioè l’entalpia per chilogrammo di aria , sarà data dalla somma dell’entalpia di 1 Kg di aria e l’entalpia di X Kg di aria , dove X è il titolo della miscela ovvero il contenuto di vapore nell’aria.
Se siamo in assenza di acqua liquida ,sia l’aria sia l’acqua possono essere considerati gas ideali. Si adottano usualmente le seguenti convenzioni:
Per l’aria:
nelle condizioni di gas ideale, alla temperatura T=0° C entalpia specifica h= 0
Per l’acqua:
alla temperatura T=0 °C entalpia specifica h=0 per il liquido sulla curva limite inferiore. (Ricordiamo che in realtà la temperatura minima sulla curva limite inferiore è quella del punto triplo , ma spesso si approssima la temperatora del punto triplo dell’acqua con il valore 0 °C).
Con queste convenzioni si ha :
![]() ( 20 )
( 20 )
Cerchiamo una espressione della ( 20 ) con i valori numerici esplicitati.
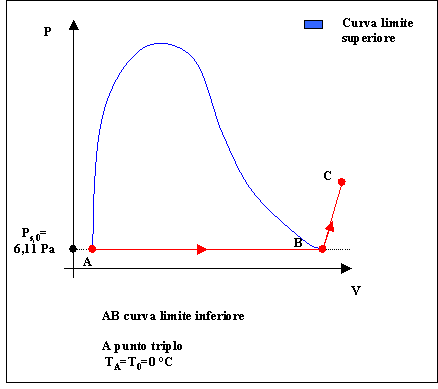
Fig. 5
Scriviamo l’equazione che descrive l’entalpia del vapore acqueo nel punto C:
![]() ( 21 )
( 21 )
Sapendo che :
Si ottiene:
![]() ( 22 )
( 22 )
dove tC è al temperatura espressa in gradi Celsius.
Dalla espressione dell’entalpia per i gas perfetti si ottiene:
![]() ( 23 )
( 23 )
ed essendo il calore specifico dell’aria cparia=1 KJ/Kg
![]() ( 24 )
( 24 )
Quindi sostituendo i valori ottenuti nella ( 20 ) si ricava:
![]()
![]() ( 25 )
( 25 )
Notiamo che la ( 25 ) è una formula dimensionalmente non omogenea , una formulazione più corretta ( che ha un significato fisico ) sarebbe :
![]() ( 26 )
( 26 )
Diagramma Psicrometrico
Sul diagramma psicrometrico è possibile individuare gli stati di equilibrio delle miscele d’aria e acqua (che possono interessare anche il dimensionamento di condizionatori e impianti per il trattamento dell’aria).
Su tale diagramma sono indicati tre assi:
Forniamo un esempio di diagramma psicrometrico ad una pressione pari a 1.013 Bar.
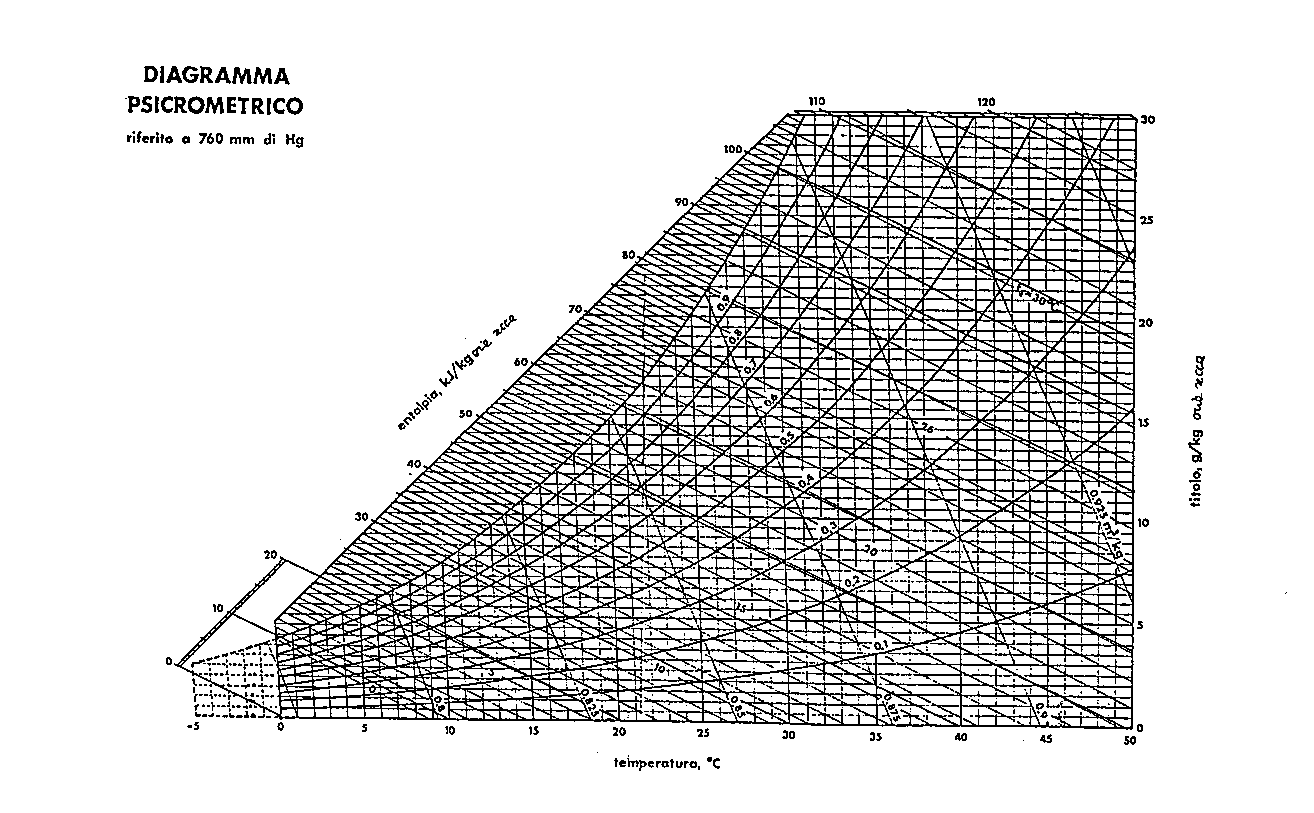
Fig .6
Per maggior chiarezza forniremo anche un diagramma esemplificativo:
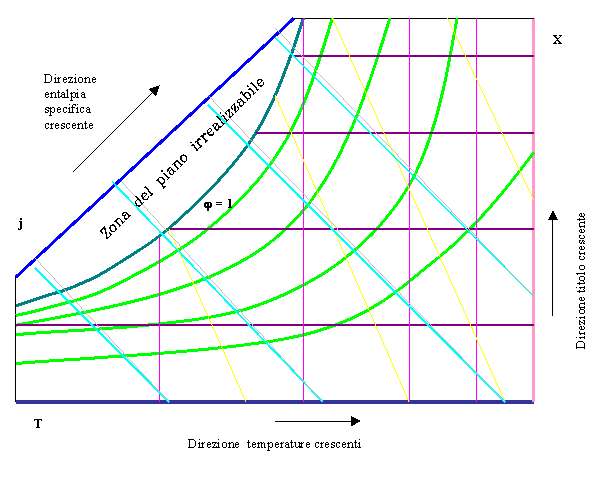 Fig .7
Fig .7
Sul diagramma sono tracciate diverse curve, vediamo quali sono:
Trasformazioni di miscele d’aria e vapore d’acqua
Vediamo ora come si rappresentano su un diagramma psicrometrico le principali trasformazioni termodinamiche (ricordiamo che il diagramma è valido se riferito ad una pressione costante e pari ad 1 Bar, altrimenti è necessario procurarsi un altro diagramma).
Consideriamo l’esperimento del recipiente d’acqua posto in un ambiente chiuso in presenza d’aria secca alla temperatura T = 20 ° C.
Il punto iniziale viene individuato sull'asse x = 0 (titolo nullo corrispondente all'aria secca). La trasformazione prosegue seguendo la retta verticale T = 20 ° C fino all’intersezione con la curva di saturazione j = 1.
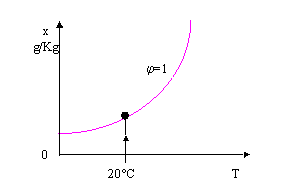
Fig. 8
A questo punto togliamo il contenitore con il liquido residuo e forniamo una certa quantità di calore Q : compiamo una trasformazione a titolo costante. Quindi ci muoviamo, partendo dal punto 1, parallelamente all’asse delle temperature fino ad arrivare al punto 2.
Il punto 2 è individuato dall’equazione :
![]() ( 27 )
( 27 )
che, in relazione alla quantità di calore fornito, fissa l’entalpia specifica corrispondente.
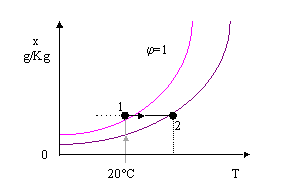
Fig. 9
A questo punto, terminato il riscaldamento, procediamo con una umidificazione dell’aria ottenuta spruzzando acqua nell’ambiente , fino ad arrivare in condizioni di saturazione.
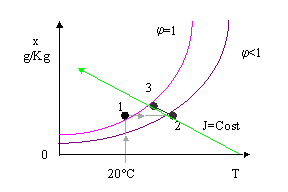
Fig. 10
Questo processo si chiama Saturazione Adiabatica e con buona approssimazione lo si può ritenere isoentalpico (j = Cost)
Quindi:
j3 = j2 dove:
![]()
![]()
Analogamente per j2:
![]()
Chiamiamo calore sensibile la grandezza ( cp’× t), prodotto tra calore specifico medio della miscela aria acqua e la temperatura alla quale la miscela si trova; e calore latente, relativo alla massa di acqua che è evaporata, la grandezza (x× r0) prodotto tra il titolo della miscela e il calore di vaporizzazione dell’acqua.
A entalpia costante il contributo del calore sensibile e quello del calore latente si bilanciano: quindi, essendo cp’ e r0 costanti, se la temperatura diminuisce il titolo dovrà aumentare; nel nostro caso dovendo essere:
j3=j2 si avrà: t3 < t2 x3 > x 2
In realtà però questo processo non è rigorosamente isoentalpico; infatti il punto finale della trasformazione dovrebbe essere individuato lungo le curve di raffreddamento adiabatico (in grigio nella figura….), che si scostano leggermente da quelle a entalpia specifica costante.
Una trasformazione a grado igrometrico costante è difficile da realizzare. Ad esempio, supponiamo di voler passare da una temperatura iniziale di T1=0 °C a T2=20 °C mantenendo il grado igrometrico costante a j =0.7.
Se mi limito a riscaldare l’ambiente fino ad arrivare a T2 avrò un abbassamento del grado igrometrico e, quindi, un’aria molto secca , praticamente irrespirabile (il corpo umano è sensibile all’umidità relativa e non al titolo).
Fig. 11
Per arrivare alle condizioni desiderate è necessario riscaldare fino ad una temperatura T>T2 sovrariscaldando l’ambiente e successivamente umidificare spruzzando acqua fino ad arrivare al grado igrometrico e alla temperatura finali.
Quindi sul diagramma psicrometrico una tale trasformazione si rappresenta nel seguente modo:
Fig. 12
Questo procedimento si utilizza negli impianti di trattamento dell’aria anche se solitamente negli impianti domestici non si rende necessaria la successiva umidificazione perché le nostre case sono ermetiche rispetto ai cambi d’aria e quindi il vapore (dovuto a doccia , cucina……) satura l’ambiente.
Ma nel caso ci siano ricambi d’aria (aprendo una finestra) sono utili soluzioni pratiche molto comuni come le seguenti:
Consideriamo ora, come ulteriore esempio, il funzionamento di un impianto di condizionamento estivo: lo scopo è di passare da una temperatura fissata T1 (che corrisponde alla temperatura dell’ambiente) ad una temperatura T2 (ovviamente più bassa).
Verranno eseguite le seguenti operazioni:
si riduce la temperatura a titolo costante fino ad arrivare alla curva di saturazione per j =1; continuando il raffreddamento lungo la curva di saturazione fino al raggiungimento della temperatura finale, una certa quantità d’acqua condenserà e verrà scolata tramite appositi condotti.
Fig. 13
Osservazione:
Nel punto C il grado igrometrico è pari a 1, cioè l’aria è satura: condizione non accettabile. Sarebbe preferibile ottenere un grado igrometrico inferiore ad una temperatura più elevata; infatti, a parità di titolo, una corrente d’aria più calda, ma avente umidità relativa inferiore ad 1 da una sensazione di fresco maggiore rispetto ad una seconda corrente d’aria più fredda ma satura (la dispersione di calore è facilitata se l’aria è più secca).
Un impianto di condizionamento più raffinato , ma più costoso, presenta anche una batteria di post-riscaldamento che riscalda l’aria mantenendo il titolo costante fino al raggiungimento di una temperatura T3 (T1<T3<T2) che corrisponde alla temperatura desiderata all’interno dell’ambiente da climatizzare raggiungendo un grado igrometrico ragionevole.
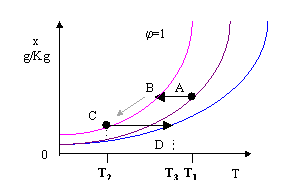
Fig. 14