Propagazione del suono in ambienti chiusi
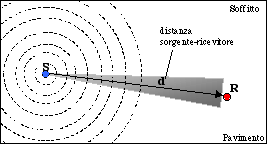
Supponiamo di avere una sorgente omnidirezionale che emette fronti d’onda sferici con uguale intensità in ogni direzione e supponiamo inoltre di collocarla in una stanza di forma perfettamente parallelepipeda (in modo da semplificarci i calcoli). All’interno di questa stanza disponiamo la sorgente S e il ricevitore R come in figura:

Figura 1 — Propagazione sonora in una stanza
All’istante t=0 la sorgente emette un impulso che si propaga con dei fronti d’onda sferici sempre più grandi. Trascorso un tempo
| (c=343 m/s è la velocità del suono nell’aria) |
necessario per la propagazione, il suono arriva al ricevitore R che per un attimo rivela un livello sonoro piuttosto elevato e poi ricade rapidamente a 0 a causa della breve durata dell’impulso. Questo livello chiamato L1 è il livello del suono diretto e rappresenta quel suono che ha viaggiato senza subire l’influenza dell’ambiente esterno, non ha, di fatto, subito fenomeni di riflessione e/o di assorbimento, in quanto ha percorso la minima distanza possibile tra sorgente e ricevitore.
Nella sua corsa il raggio sonoro interagisce anche con le pareti e ad esempio si riflette contro il pavimento. Questo suono ha percorso una distanza maggiore del suono diretto in quanto è come se provenisse da una sorgente immagine S1, lo stesso vale per il suono che si riflette sul soffitto che compie una distanza ancora maggiore ed è come se provenisse da una sorgente immagine S2 (vedi figura 2).
Questi due raggi sonori riflessi dal pavimento e dal soffitto arriveranno con dei ritardi maggiori, se il suono diretto impiegava un tempo t1 per arrivare alla sorgente, il suono riflesso sul pavimento arriverà con un ritardo
![]()
maggiore di t1, perché è maggiore la distanza d2 della sorgente immagine. Analogamente arriverà la riflessione del soffitto con un ulteriore ritardo poiché il percorso è stato maggiore.
Risulta quindi evidente che i livelli sonori sono via via più bassi a causa della legge della divergenza sferica per cui il livello sonoro cala di 6dB per ogni raddoppio di distanza, quindi maggiore è la distanza e più basso sarà il livello sonoro.
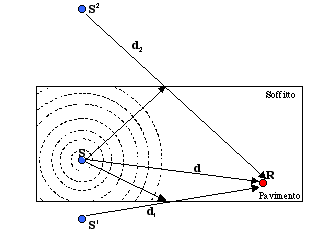
Figura 2 - Sorgenti immagine e riflessioni
Inoltre se ad esempio il pavimento ha un coefficiente di assorbimento a 1 e il soffitto ha un coefficiente a 2, è chiaro che il suono riflesso risultante sarà dato dal suono che sarebbe stato riflesso da una superficie perfettamente speculare moltiplicato per il coefficiente (1-a 1) e lo stesso per il suono riflesso dal soffitto.
Se ad esempio il soffitto è costituito da un materiale molto fonoassorbente con un coefficiente di assorbimento a 2=0,8 allora (1-a 2) =0,2 il che significa che solo il 20% dell’energia sonora incidente sul soffitto viene riflessa ad è anche per questo motivo che i raggi riflessi arrivano al ricevitore con una forte attenuazione.
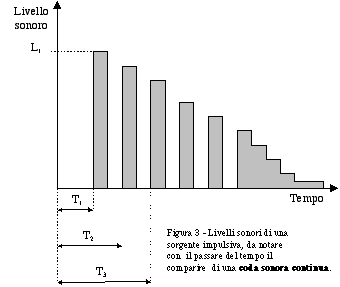
In questo semplice caso si sono presi in esame solamente i raggi riflessi dal pavimento e dal soffitto, ma nella realtà bisognerebbe prendere in esame anche tutte le altre riflessioni prodotte dalla parete posteriore, dalle pareti laterali e via dicendo. I tempi di arrivo di questi raggi tendono ad uniformarsi e l’energia da essi trasportata a calare. Nulla vieta però ai raggi di continuare a riflettersi sulle altre pareti creando raggi riflessi di ordine multiplo che si ottengono geometricamente continuando a specularizzare le sorgenti rispetto al loro piano fino a creare una vera e propria rappresentazione geometrica dei percorsi dei vari raggi sonori.
Di sorgenti immagine di ordine successivo ce ne sono una moltitudine, esse rappresentano cammini di raggi sonori dal percorso molto complicato che hanno rimbalzato un po’ su tutte le pareti accumulando ritardi e perdite di energia via via crescenti. I livelli sonori continuano a decrescere finché ad un certo punto si ha una sorta di coda sonora continua dove non è più possibile separare un’onda riflessa da un’altra in quanto ne arrivano una moltitudine negli stessi istanti di tempo provenienti da direzioni diverse ma con lo stesso centro d’arrivo (vedi figura 3).
Dato un ambiente parallelepipedo con 6 facce il numero di sorgenti del primo ordine è 6, il numero di sorgenti del secondo ordine si ottiene specularizzando ciascuna sorgente del primo ordine rispetto alle altre 5 possibili facce su cui si può riflettere e cioè 5 x 6 = 30, il processo continua in questo modo ed il numero di sorgenti immagine di ordine elevato tende ad essere enorme.
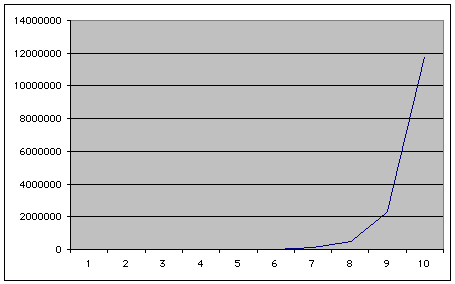
Figura 4 — Crescita esponenziale del numero delle sorgenti immagine
Il numero di sorgenti immagine esplode in maniera geometrica con l’ordine della riflessione. Quindi se di suoni riflessi una volta ne arrivano 6, di suoni riflessi due volte ne arrivano 30, di suoni riflessi 10 volte ne arrivano milioni e questi milioni arrivano con intervalli di tempo casuali creando una coda sonora statistica il cui andamento energetico è decrescente col tempo ma la cui energia decade in maniera proporzionale alla corsa del raggio ed al numero di rimbalzi (ad ogni rimbalzo perde una quota di energia pari a 1-a ).
Il coefficiente di assorbimento a può variare da rimbalzo a rimbalzo, ma su di un gran numero di impatti è plausibile usare il suo valore medio, ![]() . Non tutti i raggi rimbalzeranno nello stesso ordine, ne risulta che la coda sonora non sarà perfettamente liscia ma presenterà delle imperfezioni locali, mediamente però l’andamento della curva sarà liscio e decrescente
. Non tutti i raggi rimbalzeranno nello stesso ordine, ne risulta che la coda sonora non sarà perfettamente liscia ma presenterà delle imperfezioni locali, mediamente però l’andamento della curva sarà liscio e decrescente
Questo è il fenomeno noto come coda sonora o riverberazione che con una sorgente impulsiva è molto chiaro e ben individuabile. Le sorgenti impulsive però non sono in uso da molto, tradizionalmente il campo sonoro veniva studiato mediante sorgenti stazionarie che venivano bruscamente interrotte.
Per esempio se si smette bruscamente di suonare l’organo di una chiesa, si continua a sentirsi una coda che diminuisce sempre più di intensità. Questa situazione non corrisponde esattamente a quella precedentemente analizzata, in quanto la situazione dell’organo rappresenta una risposta in regime stazionario interrotto, che è diversa dal regime di transiente analizzato all’inizio.
Ci si può però ricondurre matematicamente alla situazione iniziale prendendo in esame la situazione di accensione di una sorgente stazionaria e non il suo spegnimento improvviso. Costruiremo quindi un diagramma con i valori dei livelli sonori che si sviluppano per l’effetto di una sorgente non più impulsiva ma stazionaria che viene accesa al tempo 0.
Trascorso il tempo t1 arriva un fronte d’onda e questo assume il valore L1 che assumeva anche con la sorgente impulsiva ammesso che la potenza delle due sorgenti sia la stessa. Siccome la sorgente non cessa dopo 1 ms come succedeva con la sorgente impulsiva ma continua ad erogare energia il livello rimane costante una volta che è arrivato il suono diretto e rimane costante fino al tempo t2 al quale arriva anche il suono prodotto dalla prima riflessione che va a sommarsi al suono dell’onda diretta.
Fatta l’ipotesi che la sorgente sia rumore incoerente, i due segnali si sommano energeticamente senza fenomeni di interferenza e quindi il livello sonoro che si raggiunge è la somma di L1 e di L2, dove L1 è il livello sonoro dell’onda diretta e L2 è il suono della prima onda riflessa.
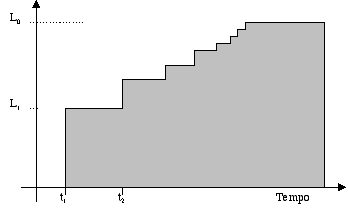
Figura 5 — Livelli sonori di una sorgente stazionaria
A questo punto il livello sonoro rimane costante fino a quando non arriva la terza onda riflessa che fa ulteriormente salire di un gradino il livello sonoro, anche se col passare del tempo e con l’arrivo di nuovi suoni i gradini diventano sempre meno alti in quanto è esperienza nota che se sommo ad un suono elevato dei suoni sempre più deboli il contributo sonoro finale tende a diventare trascurabile. Quindi con una serie di piccoli gradini corrispondenti ai singoli arrivi di energia delle singole riflessioni si giunge asintoticamente ad un livello costante L0 che rappresenta la condizione di equilibrio energetica dell’ambiente.
Volendo paragonare questa situazione con l’idraulica si potrebbe pensare ad un rubinetto che scarica acqua in un recipiente. A regime il livello che si stabilisce dentro al recipiente è tale per cui la portata di acqua che entra nel secchio è uguale alla portata di acqua che esce dal foro.

Figura 6 — Situazione di regime in idraulica
L’energia sonora in un ambiente si comporta allo stesso modo, si stabilizza ad un livello costante che corrisponde al bilancio tra la potenza che continuamente la sorgente emette e quella che continuamente le riflessioni sulle pareti stanno togliendo all’ambiente.
E’ possibile ricavare matematicamente la situazione di regime ragionando su base energetica. La grandezza che mi permette di valutare un bilancio tra l’energia immessa e quella assorbita è la densità di energia sonora e la soluzione a cui si giunge è data dalla seguente equazione:
| (1) |
Attraverso questa relazione diventa facile il calcolo del livello sonoro dentro l’ambiente che teoricamente è uguale dappertutto e passando da questa relazione alla corrispondente che ci fornisce il livello di intensità, troviamo la formula del campo riverberante, che ci fornisce il livello sonoro prodotto da una sorgente di rumore stazionario in un campo perfettamente diffuso e riverberante.
| (2) |
Questo particolare caso teorico si discosta molto dai casi reali in quanto sono molto rare le sorgenti di rumore stazionario ed anche perché è esperienza comune che il livello sonoro non sia sempre lo stesso in tutta la stanza ma vari a seconda delle distanza dalla sorgente di emissione, il concetto è che comunque esiste un suono diretto che cala di 6dB ogni raddoppio della distanza e che sono le componenti riflesse ad essere mediamente sempre le stesse in ogni punto.
Da quanto appena puntualizzato si può comprendere come in generale la formula del campo riverberante sia falsa.
Ne esiste però una versione modificata che considera la sovrapposizione energetica del livello dell’onda sferica del campo libero con il livello del campo diffuso riverberante, svolgendo i calcoli si ottiene un livello d’intensità totale dato dalla formula del campo semiriverberante:
| (3) |
Questa relazione è da tutti comunemente impiegata per valutare il campo sonoro dentro agli ambienti chiusi.
La figura 7 mostra l’andamento del livello sonoro dentro ad una stanza al variare della distanza dalla sorgente nel caso del livello sonoro della formula semiriverberante. Si tratta di un grafico in scala doppio logaritmica poiché sia la distanza dalla sorgente che il livello sonoro sono grandezze logaritmiche.
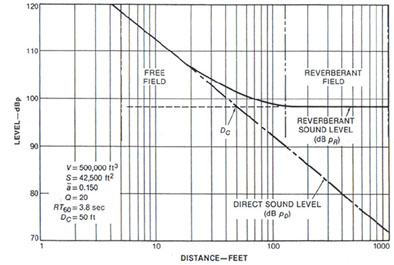
Figura 7 — Andamento del livello del suono diretto e del campo riverberante
Notiamo che la relazione teorica del campo libero corrispondente a 6dB ogni raddoppio della distanza proseguirebbe a decadere inalterata, viceversa in campo riverberante si ha questa sorta di livellamento ad un valore costante che dipende dalla superficie complessiva dell’ambiente e dal suo coefficiente di assorbimento medio, la relazione che li viene riportata è:
| (3) |
Questa relazione viene scritta in maniera leggermente diversa da chi si occupa di altoparlanti in quanto l’altoparlante non è in generale una sorgente omnidirezionale cioè che emette un’intensità uguale in tutte le direzioni. Gli altoparlanti sono di solito sorgenti direttive e si definisce la direttività Q nella direzione che stò considerando q come il rapporto tra l’intensità emessa in una certa direzione e l’intensità media emessa in tutte le direzioni. Esiste quindi un coefficiente numerico Qq che indica quanto l’altoparlante guadagna rispetto alla sua emissione media in una particolare direzione e normalmente un altoparlante è dotato di una direttività che privilegia l’emanazione in direzione frontale.
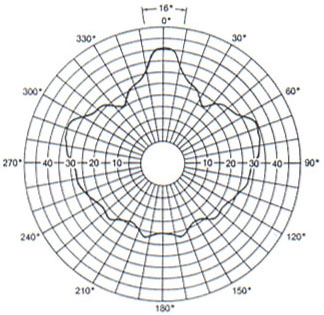
Figura 8 — Curve di direttività di un altoparlante reale
Il fattore di direttività Q può variare da poche unità a valori estremamente elevati. Quindi in presenza di una sorgente non omnidirezionale in campo diffuso mantiene la stessa rappresentazione ![]() .
.
La modifica da apportare alla formula del campo riverberante per tenere conto della direttività, è data semplicemente dalla sostituzione del fattore 1 che rappresentava l’emissione del campo diretto con il fattore Q che rappresenta ora la direttività. Ovviamente Q può essere maggiore o minore di 1. E’ maggiore di 1 se ci troviamo nel lobo di emissione dell’altoparlante, ma se ne siamo dietro o fuori sarà minore 1.
Da notare che la potenza dell’altoparlante è costante quindi se ci sono zone in cui la potenza è maggiore di 1 ci devono essere zone, la maggior parte, in cui il coefficiente sarà minore di 1. A questo punto occorre definire una grandezza fisica importante che è la distanza critica che è quella distanza dalla sorgente alla quale il campo sonoro diretto e il campo sonoro riverberante assumono lo stesso valore.
Analiticamente vale:
| (4) |
si scopre che la distanza critica dipende dal grado di assorbimento dell’ambiente, dalla sua superficie complessiva e dalla direttività e direzione dell’altoparlante.
Il concetto di distanza critica è estremamente importante in termini di qualità e comprensione del massaggio che viene riprodotto da un altoparlante. Infatti se ci si trova entro la distanza critica dalla sorgente allora si è in una situazione dove il suono diretto è predominante sul residuante campo diffuso riflesso riverberante (il suono diretto è chiaro e nitido viceversa il suono riverberante è torbido e confuso), quindi per quanto riguarda soprattutto la comprensione della parola è bene che l’ascoltatore si trovi entro la distanza critica.
In condizioni teoriche si potrebbe pensare ad un diffusore così direttivo che indirizzi il suono solo sul pubblico e non ne sprechi niente altrove.
Tale situazione può essere rappresentata come in figura 9:
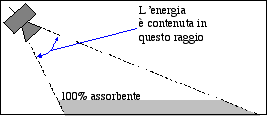
Figura 9 — Altoparlante molto direttivo
L’altoparlante è molto direttivo, il suono arriva sulle persone che hanno un forte potere fonoassorbente e non va ad eccitare il campo riverberante della stanza in quanto la stessa non riceve energia ne diretta ne riflessa. In tale situazione il campo sonoro è tutto diretto anche se il tempo di riverbero dell’ambiente è alto.
Viceversa la situazione rappresentata in figura 10 è un caso molto felice perché è il caso di un altoparlante poco direttivo posizionato in un ambiente senza riverbero, quindi riesce sempre ad emettere un suono diretto forte poiché il riverbero dell’ambiente è nullo. L’altoparlante direttivo ha efficacia solo se è ben posizionato.
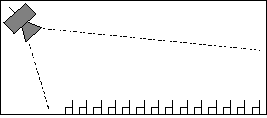
Figura 10 — Altoparlante poco direttivo
La problematica analizzata fino a questo punto è stata esaminata con l’aiuto di un segnale stazionario, ma la situazione in cui l’analisi si complica enormemente è quando il segnale varia nel tempo, quando cioè c’è un forte altalenarsi di suoni deboli e forti a diverse frequenze come ad esempio la voce umana.
In queste situazioni i concetti di livello sonoro (diviso nella sua parte diretta e riverberante) e distanza critica non sono più sufficienti a descrivere il fenomeno nella sua completezza.
Accingiamoci dunque a rifare il processo che ci ha portato alla costruzione del campo sonoro riverberante complessivo. Giunti a regime e quindi a livello complessivo L0 ad un certo istante t1 spegniamo la sorgente sonora che emanava il segnale stazionario. L’ascoltatore posto alla distanza d istantaneamente non si accorge che la sorgente è stata spenta e fino al tempo uguale a t1 il suono continua ad arrivare (non viene più emesso ma quello che era nell’aria continua ad arrivare).
Trascorso il tempo t1 viene a mancare il contributo del suono diretto e c’è da notare che quando dal silenzio è arrivato il suono diretto la differenza si è sentita molto, mentre adesso tra tutti gli altri suoni il fatto che non ci sia più il suono diretto non è così evidente e questo spiega il fatto per cui il grafico ha in salita dei gradini molto evidenti ed in discesa sia così attenuato.
Trascorre poi il tempo tra t1e t2 con il livello che rimane costante, dopo t2 se ne va la prima onda riflessa che fa un gradino ancora più minuscolo , dopo di che se ne va la seconda onda riflessa e via così se ne vanno tutte le altre dando origine ad una curva di decadimento che è molto liscia.
Mentre la risposta all’impulso era molto irregolare, la coda di decadimento del rumore stazionario interrotto è molto liscia e si dimostra matematicamente che questa curva su di un diagramma lineare nel tempo è una retta.
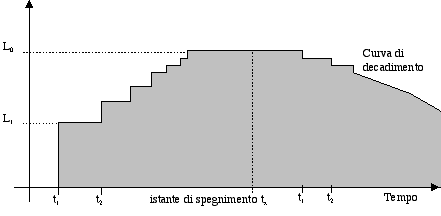
Figura 11 — Curva di decadimento di una sorgente sonora stazionaria
Per il primo livello di decibel c’è un decadimento sonoro che se ne va linearmente col tempo almeno (se ne vanno tot decibel ogni secondo). Questo è il fenomeno che fu studiato da Sabine all’inizio del secolo e che porta alla formulazione della durata convenzionale della coda sonora chiamata anche tempo di riverberazione o di riverbero.
Il tempo di riverbero è definito come il tempo necessario affinché il livello sonoro decada di 60 dB ed è chiamato T60.
Ovviamente nel fare questa valutazione è bene uscire dalla parte irregolare del grafico e farla nel tratto liscio che segue. Secondo la normativa ISO3382 del 1997 il tratto su cui valutare la pendenza media della curva deve iniziare a —5dB rispetto al livello L0 che si aveva con la sorgente in funzione. Operativamente, bisogna spegnere la sorgente, attende che il livello decresca di 5dB, far partire un cronometro, aspettare che il livello arrivi a —65dB ed infine fermare il cronometro.
Il tempo che è passato viene detto tempo di riverberazione T60 ed è il parametro primario che caratterizza quanto un ambiente è riverberante o meno.
Il coefficiente di assorbimento medio è in qualche modo legato al tempo di riverberazione (mediante la formula di Sabine). Però il coefficiente di assorbimento medio non fornisce direttamente il valore del tempo di riverbero, perché dipende anche dalla superficie dell’ambiente. Il tempo di riverbero indica invece direttamente l’effetto percepibile dall’uomo della durata della coda sonora in secondi.
L’ambiente è molto riverberante quando il tempo di riverbero supera i 2 secondi, viceversa è molto asciutto se il tempo di riverbero è sotto al secondo. Quindi la regolazione del tempo di riverbero in un ambiente è uno dei principali parametri di progettazione acustica ad esempio di una sala concerti. Vari tipi di utilizzo della sala richiedono valori diversi del tempo di riverberazione ottimale:
| | |
| Aula piccola | 0,5s |
| Aula grande | 1,0s |
| Cinema | 0,7s ÷ 0,8 s |
| Teatro d’epoca | 1,3s ÷ 1,5 s |
| Concert Hall | 1,7s ÷ 2,3 s |
| Chiesa | 8,0s ÷ 10 s |
Quindi esiste un tempo di riverbero ottimo a seconda del tipo di utilizzo della sala.
Dal punto di vista ingegneristico l’unica cosa che occorre è poter quantificare il valore di tempo di riverbero partendo dalle caratteristiche acustiche dell’ambiente e questo lo si fa con la formula di Sabine:
| (5) |
l’unica difficoltà è conoscere il coefficiente di assorbimento (vedi esercizio 1).
Il coefficiente medio lo si troverà poi come media dei coefficienti di assorbimento delle varie parti della stanza:
| (6) |
e quindi posso scrivere
| (7) |
ESERCIZIO n.1
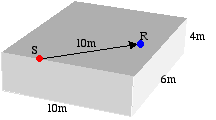
Dati problema:
Coefficienti di assorbimento:
pavimento a 1 = 0,05
pareti a 2 = 0,1
soffitto a 3= 0,6
Distanza della sorgente S dal ricevitore R = 10m
Potenza sonora della sorgente LW=100dB
Calcolare:
LDIR (livello del suono diretto)
LRIV(livello del suono riverberante)
LTOT (livello del suono complessivo)
R/D (livello suono riverberante fratto livello suono diretto, indica quale dei due livelli sonori sta predominando)
T60 (tempo di riverbero)
Svolgimento:
| Livello suono diretto: | |
| Livello suono riverberante: | |
| dove | |
| (60=superficie del pavimento=sup. del soffitto, 128=sup. delle pareti laterali) | |
| Distanza critica: | |
| Livello totale: | |
| R/D = 88,9-69 = 19,9 dB | |
| (0,16 è un valore empirico, la formula non è dimensionalmente esatta). |
Da questi calcoli si può notare come un ascoltatore posto a 10m dalla sorgente in un ambiente che non è dotato di un riverbero molto alto riceve un campo sonoro in massima parte riverberante e in minima parte diretto e quindi di fatto sente male.
ESERCIZIO n.2
Si parte da una misura del tempo di riverbero e si vuole calcolare il coefficiente di assorbimento del materiale. Si prende una stanza di prova chiamata camera riverberante e si misura il tempo di riverberazione dapprima a stanza vuota e poi si ripete la misura dopo aver inserito il materiale fonoassorbente.
Di solito le stanze sono di forma irregolare per evitare che si creino onde stazionarie o treni d’onda.
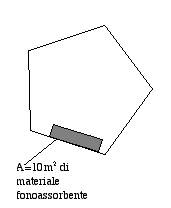
Situazione di partenza:
Volume stanza: V= 220m3
Superficie interna: S= 190 m2
Tempo di riverbero a stanza vuota: (T60)1= 11s
Tempo di riverbero con il materiale: (T60)2= 4s
Svolgimento:
| determino |
| determino l’incognita |
Questa tecnica è comunemente impiegata per misurare il coefficiente di assorbimento dei materiali da utilizzare. La norma ISO che regola questo tipo di misura è la ISO354. Il guaio di questa tecnica è che esistono dei materiali cosi assorbenti che dopo aver fatto i calcoli esce un valore di a maggiore di 1 che è un assurdo (come fa la superficie ad aver assorbito più energia di quanta ne ha ricevuta).
Questo deriva dal fatto che la formula di Sabine funziona bene solo con ambienti che hanno un coefficiente di assorbimento medio minore di 0,5. E’ un fatto noto che usando la norma ISO354 si possono ottenere valori superiori a 1, infatti sul catalogo del materiale si indica che il valore riportato è stato misurato secondo la norma ISO354 o a di Sabine.
Il grosso vantaggio è che il valore precedentemente trovato se reinserito nella formula di Sabine fornisce un valore del tempo di riverbero perfettamente corretto, in parole povere non ha molta importanza ai fini pratici se il valore è sballato se poi usato nella formula porta a dei risultati corretti. Con a SABINE e l’uso della formula di Sabine si ottengono risultati esatti con un a "vero" bisognerebbe usare un programma di simulazione che riproduca il comportamento della stanza ed i calcoli sarebbero enormemente più complicati.
Misura del tempo di riverbero
Esistono una vasta categoria di tempi di riverbero, T10, T30, T40, tutti questi valori sono però tra loro equivalenti, in quanto anche se vengono cronometrati su decadimenti più corti, (poiché è molto difficile in situazioni reali il verificarsi di un decadimento sonoro di 60dB, necessario per il calcolo del T60, tenendo conto anche del rumore di fondo), essi sono sempre estrapolati al T60 corrispondente.
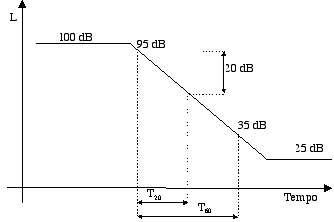
Figura 12 — Misure del tempo di riverbero
Si definisce ad esempio il valore di T20, ma il valore che si trova dalla misura del T20 sarebbe 1/3 del T60 e quindi la gente si confonderebbe perché parlando di tempo di riverbero bisognerebbe sempre specificare a quale T è stato misurato, allora l’ISO stabilisce che il valore trovato (sia esso un T10 o un T15 per esempio) deve essere estrapolato al T60 corrispondente.
Per fare un esempio il T20 trovato lo si triplica e lo si chiama ancora T20. Quindi formalmente anche T20 è il tempo necessario per il decadimento di 60dB solo che è stato misurato estrapolando i primi 20 dB.
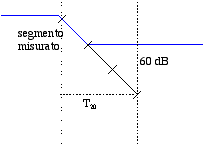
Figura 13 — Estrapolazione del T20 al T60
Non è vero quindi che T10 è la metà di T20, formalmente hanno lo stesso valore. La ISO354 prevede la misura di T30 non di T60 perché anche in laboratorio è difficile avere un decadimento di 60dB.
Calcolo del decadimento sonoro mediante la risposta all’impulso
Il problema che ci prepariamo a risolvere è quello classico del calcolo del decadimento sonoro di una sorgente stazionaria mediante la misura della risposta all’impulso.
Il livello complessivo L0 è dato da:
| (8) |
Il livello corrente è invece dato da:
| (9) |
In termini numerici, attraverso le forme d’onda campionate è possibile misurare una risposta all’impulso in una sala ad esempio con un colpo di pistola. Avendo generato questo segnale impulsivo si procede poi a campionare una serie di numeri (esempio un numero ogni ms) che rappresentano l’intensità sonora.
Mediante un foglio elettronico, ad esempio Excel, si riportano sulla prima colonna i vari tempi di campionamento e sulla seconda colonna i valori delle intensità.
Attraverso un semplice calcolo su di una terza colonna si è in grado di trovare in maniera molto semplice i due valori estremi su cui basare il calcolo del tempo di riverbero (vedi figura 14).
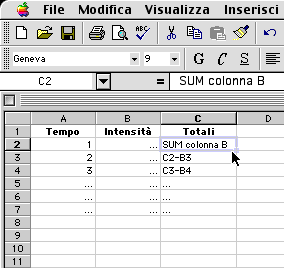
Figura 14 — Schermata di esempio di Excel
La prima cella della terza colonna conterrà la somma di tutta la seconda colonna, la seconda cella della terza colonna conterrà di nuovo questa somma sottratta dal valore della cella B3 e cosi via.
Continuando questo procedimento per tutti i valori campionati si ottiene una lista di valori e sarà proprio partendo da questi dati che bisognerà cercare gli istanti di inizio e di fine necessari per il calcolo del tempo di riverbero.
Questo procedimento matematico è noto come integrazione all’indietro di Schroder, che ha il merito di aver inventato un procedimento molto veloce che permette in maniera molto semplice il calcolo del decadimento di un suono stazionario interrotto (tempo di riverbero) in una stanza mediante la misura della risposta all’impulso.
E’ solo da dopo questa invenzione (1975) che si è incominciato a misurare in maniera sistematica il tempo di riverbero mediante la risposta all’impulso.