Michele Amoretti, n.matricola 95645
lezione del 26/10/99, ore 16:30-18:30
LA MACCHINA DI RANKINE
Il problema di realizzare un ciclo termodinamico che produca la massima quantità di lavoro a parità di calore entrante, ha come soluzione ottimale la macchina di Carnot. Si tratta però di una macchina ideale, perché opera su un ciclo reversibile.
Nella pratica, la soluzione che in maniera più brillante approssima quella ottimale è la macchina di Rankine:

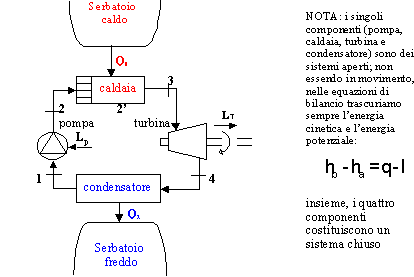
Fig.1 - schema della macchina di Rankine
La macchina di Rankine ha avuto e ha tuttora innumerevoli applicazioni: dalla locomotiva a vapore, alle centrali termoelettriche a combustibile chimico o nucleare. Normalmente, il fluido che descrive il ciclo è l’acqua.
Per studiarne il funzionamento, possiamo ricorrere a tre tipi di diagramma:
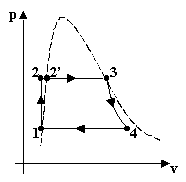
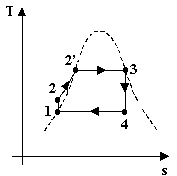
Fig.2 - diagrammi pressione-volume, temperatura-entropia, entalpia-entropia
Il primo è il più intuitivo, ma il secondo è il più importante (il terzo è per uso specialistico).
Facciamo dunque riferimento al diagramma T-s e spieghiamo il ciclo passo-passo:
1® 2: il fluido, che è nella fase liquida, subisce una compressione isoentropica (s è costante); ciò viene realizzato mediante una pompa, sistema aperto che non scambia calore:
![]() (1)
(1)
2® 2’, 2’® 3: il fluido viene prima riscaldato e poi vaporizzato, sempre a pressione costante; si utilizza una caldaia, sistema aperto che non scambia lavoro:
![]() (2)
(2)
![]() la quantità di calore q1 viene prelevata dai fumi caldi prodotti dalla combustione di un combustibile e dell’aria comburente
la quantità di calore q1 viene prelevata dai fumi caldi prodotti dalla combustione di un combustibile e dell’aria comburente
3® 4: il fluido, che ora è nella fase di vapore saturo secco, passa attraverso a una turbina, sistema aperto che non scambia calore, e, espandendosi isoentropicamente, compie lavoro:
![]() (3)
(3)
4® 1: il fluido, nello fase di vapore saturo a bassa pressione, viene portato completamente nella fase liquida, a pressione e temperatura costanti; per fare ciò, si utilizza un condensatore, che cede la quantità di calore
![]() (4)
(4)
a una serpentina (serbatoio freddo)
Calcoliamo il coefficiente economico e , rapporto tra lavoro prodotto e calore assorbito netti:
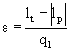 (5)
(5)
ossia, da (1),(2) e (3):
![]()
Ora, poiché in 1® 2 il fluido è nella fase liquida:
![]() (7)
(7)
dove v (= v1 = v2 , i liquidi sono incomprimibili; il valore per l’acqua è 1 dm3/kg) e p1,p2 sono tabulate in funzione di T.
Per gli stati 3 e 4, in cui il fluido è nella fase di vapore saturo, vale la formula:
![]() (8)
(8)
dove hl(p,T) è l’entalpia sulla curva limite inferiore (tabulata), r(p,T) è il calore latente di vaporizzazione (tabulato) e x il titolo. Quest’ultimo vale 1 per lo stato 3 (la massa di vapore coincide con la massa totale del fluido); va invece calcolato per lo stato 4, sfruttando il fatto che la trasformazione 3® 4 è isoentropica:
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
da cui:
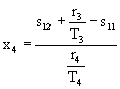 (12)
(12)
dove sl(p,T) è l’entropia sulla curva limite inferiore (tabulata).
Notiamo poi che la (6) può essere così riscritta:
![]() (13)
(13)
e che quindi:
![]() (14)
(14)
Confrontiamo il ciclo di Rankine e il ciclo di Carnot (perché ciò abbia senso, devono operare tra le stesse temperature):
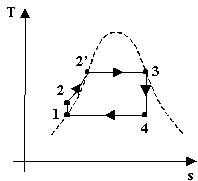
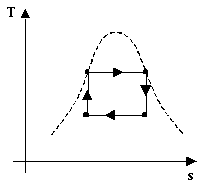
Fig.3 - ciclo di Rankine e ciclo di Carnot, diagramma T-s
il ciclo di Rankine presenta delle irreversibilità; ad esempio, il fatto che man mano che si prende calore dai fumi di combustione la loro temperatura diminuisca, è una causa di irreversibilità esterna; il fluido è comunque sempre in equilibrio termodinamico, per cui l’area del ciclo nel diagramma rappresenta la differenza tra il calore assorbito e il calore ceduto, cioè il lavoro prodotto, come per il ciclo di Carnot. Guardando le figure, è lecito aspettarsi che il rendimento termodinamico
![]()
![]() (15)
(15)
(rapporto tra il coefficiente economico della macchina di Rankine e quello della macchina di Carnot) assuma un valore prossimo all’unità.
Esercizio numerico
Determinare il coefficiente economico e per un ciclo di Rankine con
T1 = T4 = 40 ° C
T2 = T3 = 250,3 ° C
Da (7):
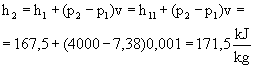
Da (8):
![]()
Da (12):
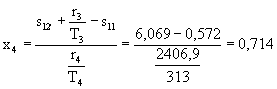
Da (8):
![]()
Quindi, da (6):
![]()
Facciamo un confronto con il ciclo di Carnot:
![]()
Quindi:
![]()
MACCHINA DI RANKINE CON SURRISCALDATORE
Abbiamo visto che il vapore saturo secco in uscita dalla caldaia viene fatto espandere utilizzando una turbina; ma poiché nello stato 4 il titolo è abbastanza minore di 1, ci sono gocce di liquido che entrano in violento contatto con le parti meccaniche della turbina e le erodono.
In genere si adotta la seguente soluzione:
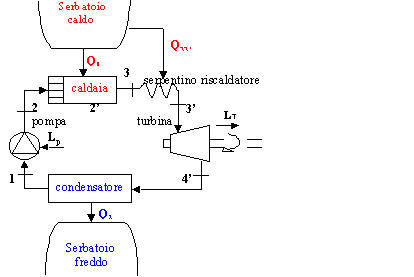
Fig.4 - schema della macchina di Rankine con surriscaldatore
Il serpentino riscaldatore fa sì che il fluido in uscita dalla caldaia passi dalla fase di vapore saturo secco in quella di vapore surriscaldato.
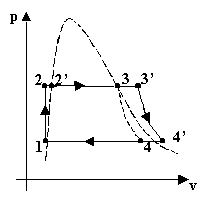
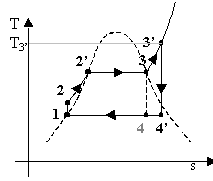
Fig.5 – diagrammi pressione-volume, temperatura entropia
E’ evidente che il valore del titolo nello stato 4’ è molto più vicino a 1.
La nuova formula per il coefficiente economico è:
![]() (16)
(16)
Per lo stato 3’ vale la formula:
![]() (17)
(17)
da cui ricaviamo il calore specifico medio a pressione costante cp, leggendo h3’ dalla tabella del vapore surriscaldato (o viceversa ricaviamo h3’ leggendo cp dalla relativa tabella).
Per h4’ usiamo la (8), con x4’ ricavato da:
![]() (18)
(18)
dove s3 è data dalla (10).
Esercizio numerico
Determinare il cefficiente economico per un ciclo di Rankine con surriscaldamento, date:
T1 = T4 = 40 ° C
T2 = T3 = 250,3 ° C
T3’= 500 ° C
Da (17):
![]()
Da (18):
![]()
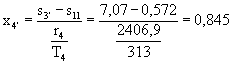
Da (8):
![]()
Quindi, da (16):
![]()
NOTA:
Per confrontare la macchina di Rankine con surriscaldatore e la macchina di Carnot, è sbagliato calcolare h t come rapporto tra i coefficienti economici con
![]()
Si otterrebbe 0,635: apparentemente peggio rispetto al caso della macchina di Rankine senza surriscaldatore!
L’errore sta nel fatto che si sta fornendo alla macchina di Carnot più calore di quello dato alla macchina di Rankine con surriscaldatore:
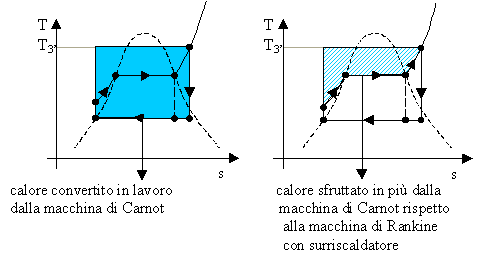
Fig.6 – confronto tra le quantità di calore
Bisogna guardare il diagramma che descrive l’andamento della temperatura del serbatoio caldo (fumi prodotti bruciando combustibile e aria) in funzione della quantità di calore da esso sottratta, e confrontare le due macchine in base alla quantità di calore che effettivamente riescono a sfruttare (exergia):
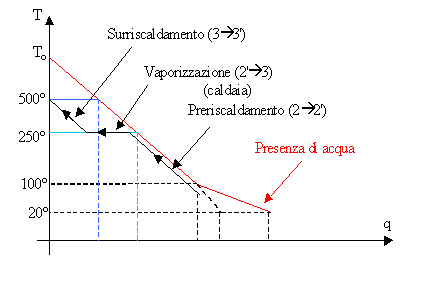
Fig.7 – in rosso: diagramma T-q del serbatoio caldo, in nero: trasformazione 2® 3 nel ciclo di Rankine con surriscaldamento, in blu e celeste: due esempi di passaggi analoghi nel ciclo di Carnot
Concludendo, solo con un’infinita successione di cicli di Carnot si riesce ad estrarre tutto il calore dai fumi:
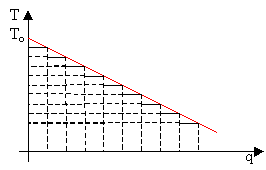
Fig.8 – estrazione totale del calore per mezzo di infiniti cicli di carnot
La macchina di carnot sarebbe ottima se il serbatoio caldo fosse a temperatura costante.
Esercizio numerico conclusivo
Calcolare il CUC (coefficiente di utilizzazione del combustibile = rapporto tra l’energia utilizzata e quella disponibile in partenza) di una centrale di cogenerazione, che funzione secondo il principio della macchina di Rankine con surriscaldatore (e sfrutta Q2 per il riscaldamento cittadino), noti i seguenti dati:
T1 = T4 = 80 ° C
P3 = 40 BAR
T3’ = 700 ° C
h distr = 95% (percentuale di Q2 effettivamente sfruttata)
h comb = 90% (Q1 non è tutto il calore generato nel serbatoio caldo)
E’ facile vedere che, nel caso in esame:
![]()
Dalle tabelle, poi, leggo:
T1 = 80 ° C Û p1= 0,4736 BAR
p3 = 40 BAR Û T3 = T2 = 250,3 ° C
h1 = hl1 = 340,5 kJ/kg
r4 = 2305,4 kJ/kg
Dagli esercizi precedenti, prendo pari pari v, h3 e s3.
Quindi, da (17):
![]()
Da (18):
![]()
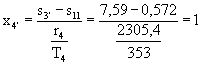 (4’ è sulla curva limite!)
(4’ è sulla curva limite!)
Allora, da (8):
![]()
Poi, da (3), (2), (4) e (7):
![]()
![]()
![]()
![]()
E infine:
![]()
Molto bene! Una centrale Enel tradizionale ha un CUC @ 0,4.
|
T (° C) |
p (BAR) |
hl (kJ/kg) |
r (kJ/kg) |
sl (kJ/kgK) |
|
0,01 |
0,006112 |
0 |
2501,6 |
0 |
|
4 |
0,008129 |
16,8 |
2492,1 |
0,0611 |
|
8 |
0,010720 |
33,6 |
2482,6 |
0,1213 |
|
12 |
0,014014 |
50,4 |
2473,2 |
0,1805 |
|
16 |
0,018168 |
67,1 |
2463,8 |
0,2388 |
|
20 |
0,023366 |
83,9 |
2454,3 |
0,2963 |
|
24 |
0,029821 |
100,6 |
2444,9 |
0,3530 |
|
28 |
0,037782 |
117,3 |
2435,4 |
0,4088 |
|
32 |
0,047534 |
134,0 |
2425,9 |
0,4640 |
|
36 |
0,059400 |
150,7 |
2416,4 |
0,5184 |
|
40 |
0,073750 |
167,5 |
2406,9 |
0,5721 |
|
44 |
0,091001 |
184,2 |
2397,3 |
0,6252 |
|
48 |
0,11162 |
200,9 |
2387,7 |
0,6776 |
|
52 |
0,13613 |
217,6 |
2378,1 |
0,7293 |
|
56 |
0,16511 |
234,4 |
2368,4 |
0,7804 |
|
60 |
0,19920 |
251,1 |
2358,6 |
0,8310 |
|
64 |
0,23912 |
267,8 |
2348,8 |
0,8809 |
|
68 |
0,28563 |
284,6 |
2338,9 |
0,9303 |
|
72 |
0,33958 |
301,4 |
2329,0 |
0,9792 |
|
76 |
0,40191 |
318,1 |
2318,9 |
1,0275 |
|
80 |
0,47360 |
334,9 |
2308,8 |
1,0753 |
|
84 |
0,55573 |
351,7 |
2298,6 |
1,1225 |
|
88 |
0,64948 |
368,5 |
2288,4 |
1,1693 |
|
92 |
0,75608 |
385,4 |
2278,0 |
1,2156 |
|
96 |
0,87686 |
402,2 |
2267,5 |
1,2615 |
|
100 |
1,01325 |
419,1 |
2256,9 |
1,3069 |
|
104 |
1,1668 |
435,9 |
2246,3 |
1,3518 |
|
108 |
1,3390 |
452,9 |
2235,4 |
1,3964 |
|
112 |
1,5316 |
469,8 |
2224,5 |
1,4405 |
|
116 |
1,7465 |
486,7 |
2213,4 |
1,4842 |
|
120 |
1,9854 |
503,7 |
2202,2 |
1,5276 |
TAB.1 – Vapore Saturo
|
T (° C) |
h (kJ/kg) |
s (kJ/kgK) |
|
250 |
2800,3 |
6,0685 |
|
300 |
2962,0 |
6,3642 |
|
350 |
3095,1 |
6,5870 |
|
400 |
3215,7 |
6,7733 |
|
450 |
3331,2 |
6,9388 |
|
500 |
3445,0 |
7,0909 |
|
550 |
3558,6 |
7,2333 |
|
600 |
3672,8 |
7,3680 |
|
650 |
3787,9 |
7,4961 |
|
700 |
3906,6 |
7,5947 |
TAB.2 – Vapore surriscaldato
(p = 40 BAR, hl = 1087,4 kJ/kg)
Tabelle più complete si trovano su: Zemanski "Termodinamica per ingegneri"
|
T (° C) |
cp (kJ/kgK) |
|
300 |
3,136 |
|
350 |
2,891 |
|
400 |
2,742 |
|
450 |
2,648 |
|
500 |
2,579 |
|
550 |
2,533 |
|
600 |
2,500 |
|
650 |
2,475 |
|
700 |
2,458 |
TAB.3 – Calore specifico medio del vapore surriscaldato
(p = 40 BAR, hl = 1087,4 kJ/kg)