Vediamo come e' possibile analizzare un segnale audio attraverso un personal computer, con l'ausilio di specifici software:

• Cool Edit (www.syntrillium.com): è un editor di forme d'onda, e può mostrare anche l'analisi in frequenza attraverso la Fast Fourier Transform (FFT). Contiene anche un generatore di segnali.
• SpectraRTA (www.soundtechnology.com): analizza il segnale in terzi d'ottava, e permette, ad es., di vedere lo spettro ponderato A.
• SpectraLAB (www.soundtechnology.com): è il più completo, permettendo la visualizzazione sia della forma d'onda che degli spettri FFT e in terzi d'ottava. Come SpectraRTA, può generare vari tipi di segnali, come le Frequency Sweep.

Usando Cool Edit registriamo (a 44.100 Hz, 16 bit stereo) il tono di calibrazione, un segnale con frequenza di 1 KHz a 94dB, che serve appunto a calibrare gli strumenti di misura. In questo caso il tono è stato generato con il programma SpectraRTA, mentre se bisogna calibrare un fonometro si usa uno specifico strumento, il calibratore, che emette il tono puro che si fa registrare dal fonometro.

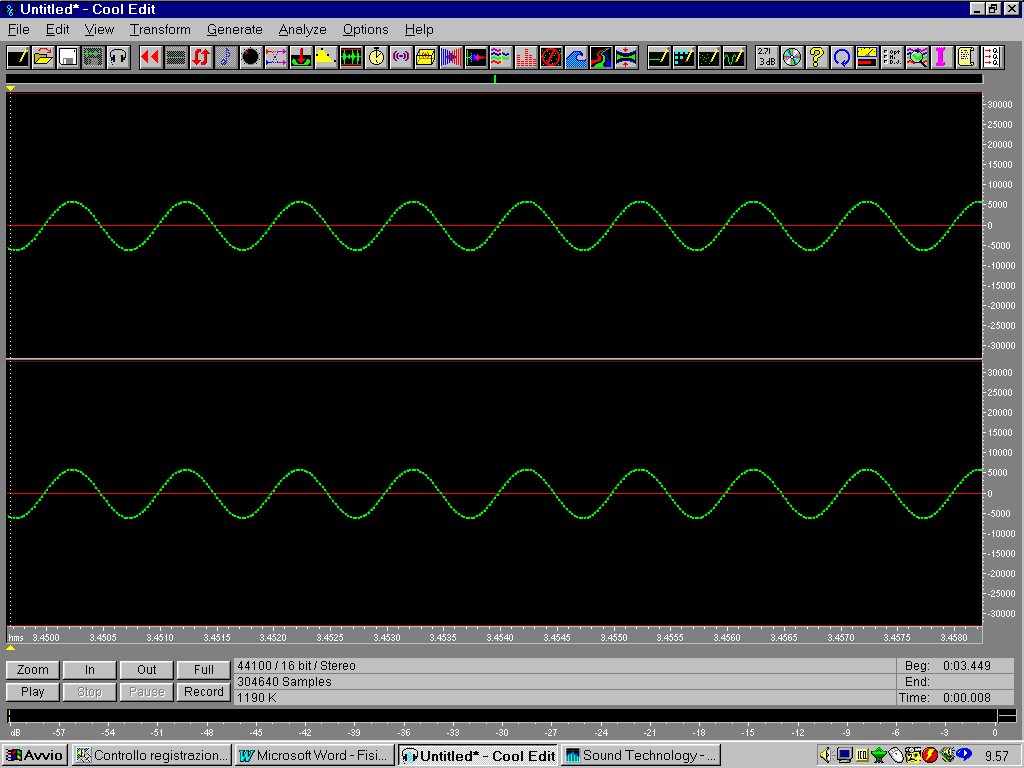
In fig. 1 si può vedere la forma d'onda del tono puro. Attraverso il programma si possono apportare modifiche: si può modificare la sinusoide, tagliare pezzi indesiderati ecc. Ma quando si elimina una parte della forma d'onda e i due estremi non coincidenti vengono "attaccati" dal programma si forma un gradino: osservando l'analisi in frequenza di questo gradino (sempre attraverso CoolEdit), si nota la discontinuità prodotta dalla modifica al segnale. L'analisi in frequenza viene eseguita calcolando la Fast Fourier Transform (FFT) sul segnale. Grazie ad essa si può vedere da quali frequenze è composto il segnale e la loro intensità.

Fig. 1 - Forma d'onda del tono puro di 1KHz

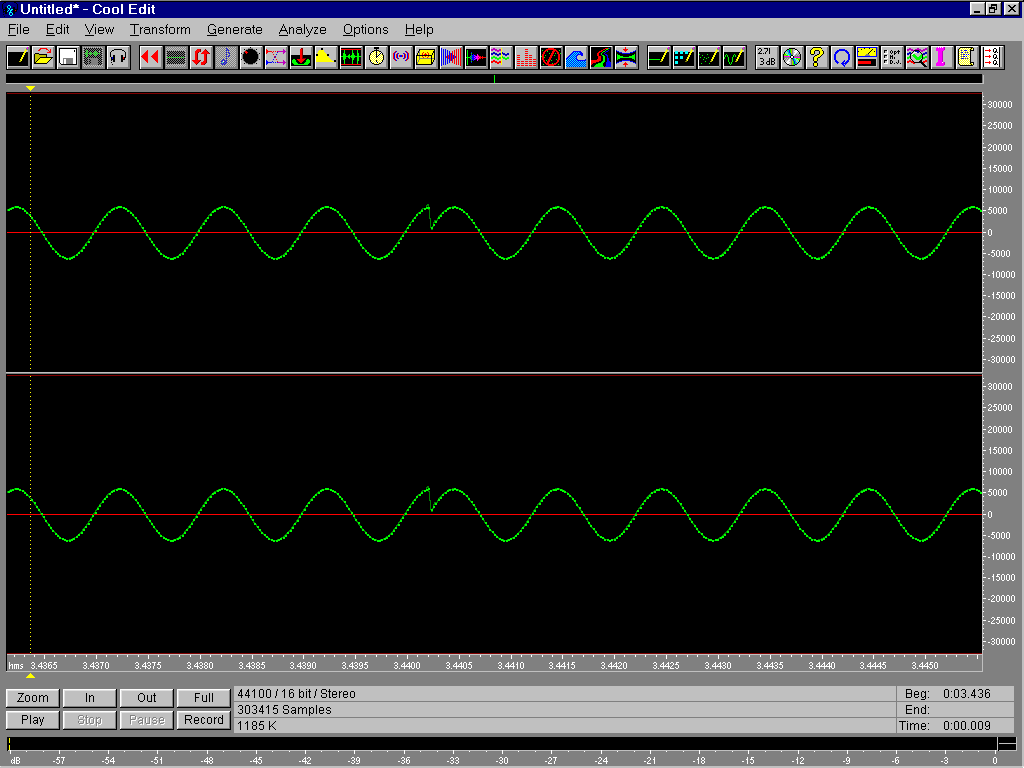
Fig. 2 - effetto dell'asportazione di una parte del segnale

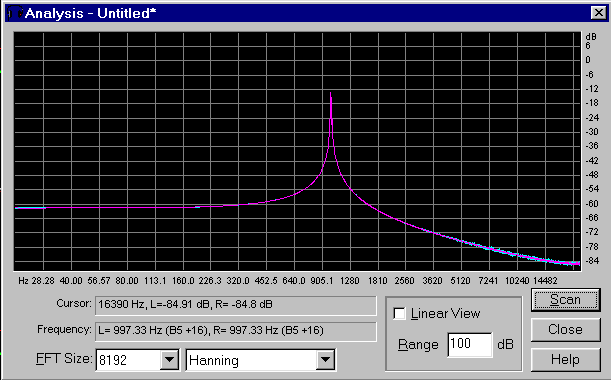
Fig. 3 - Spettro in frequenza del gradino

Dalla fig. 3 si vede chiaramente che nel gradino non c'è solamente la componente ad 1 Khz, ma sono comparse altre frequenze. Questa analisi, come si vede dall'immagine, è stata fatta con una risoluzione di 8192 linee e usando il filtro Hanning. Nella prossima immagine si vede invece lo spettro del tono normale, e si vede chiaramente la sola componente ad 1 Khz.

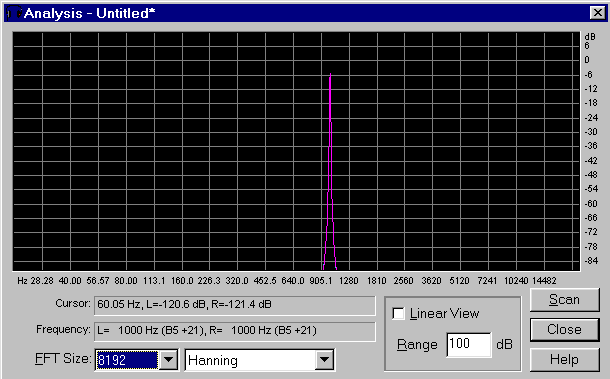
Fig. 4 - Spettro in frequenza del tono puro a 1KHz

Vediamo ora un segnale più complesso. Con Cool Edit si possono generare due segnali particolari (oltre a vari altri tipi): il rumore bianco e il rumore rosa. Il primo ha uno spettro piatto su un analizzatore a banda stretta (ogni frequenza ha la stessa energia), mentre il secondo ha uno spettro piatto su un analizzatore in terzi d'ottava (le alte frequenza hanno meno energia delle basse). Inoltre il rumore rosa contiene più basse frequenze.

Analizziamo i due rumori in frequenza, attraverso la FFT. Le due immagini seguenti (ottenute riducendo la FFT Size a 4096) mostrano gli spettri del rumore bianco e di quello rosa: si vede che il primo è sostanzialmente piatto (uniforme su tutte le frequenze), mentre il secondo scende di 3dB per ottava. Questo perché ogni ottava è larga il doppio di quella precedente e quindi prende il doppio di energia. Di conseguenza l'energia del segnale deve essere la metà rispetto all'ottava precedente se voglio che il livello totale di energia di ogni ottava sia uguale a quello precedente.

Un altro tipo di rumore, il rumore marrone, scende di 6dB per ottava.

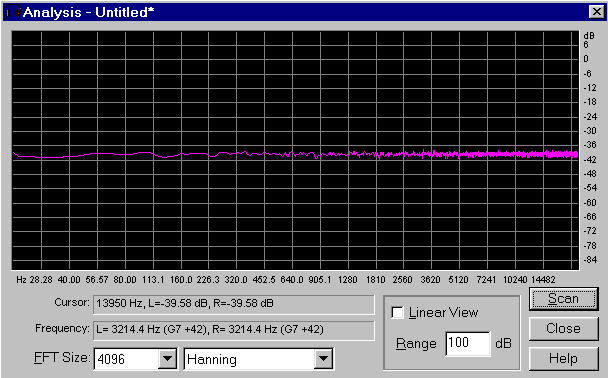
Fig. 5 - Analisi in frequenza del rumore bianco

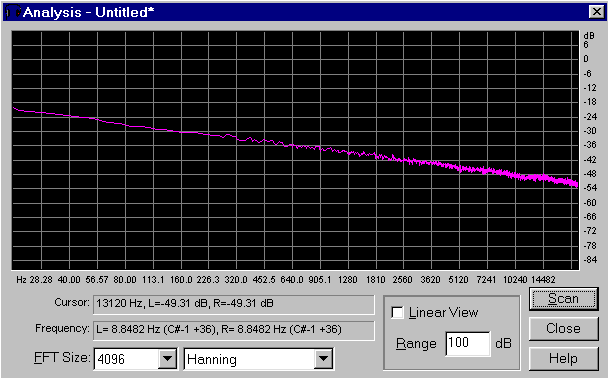
Fig. 6 - Analisi in frequenza del rumore rosa

Adesso verifichiamo che il rumore bianco, analizzato in terzi d'ottava, non ha per nulla uno spettro piatto. Per fare questo si utilizza il software SpectraRTA, un analizzatore in terzi d'ottava.

La prima cosa da fare è calibrare il software. Infatti, se si prova generando un tono puro da 1KHz (attraverso il generatore di segnali incluso in SpectraRTA) a 94dB, si vede che il programma visualizza un valore in dB errato. Quindi attraverso l'apposita funzione (options à calibration) occorre calibrarlo, verificando poi che il tono sia esattamente valutato 94dB.

Nell'immagine seguente il rumore bianco appare crescente di 3dB per ottava: questo perché la forma di uno spettro cambia secondo l'analizzatore utilizzato; inoltre coincide con il fatto che abbia lo spettro FFT piatto. Inoltre bisogna notare che l'asse delle frequenze è logaritmico (in SpectraRTA non si può avere l'asse lineare). Infatti, normalmente le analisi in terzi d'ottava sono fatte con l'asse delle frequenze logaritmico.

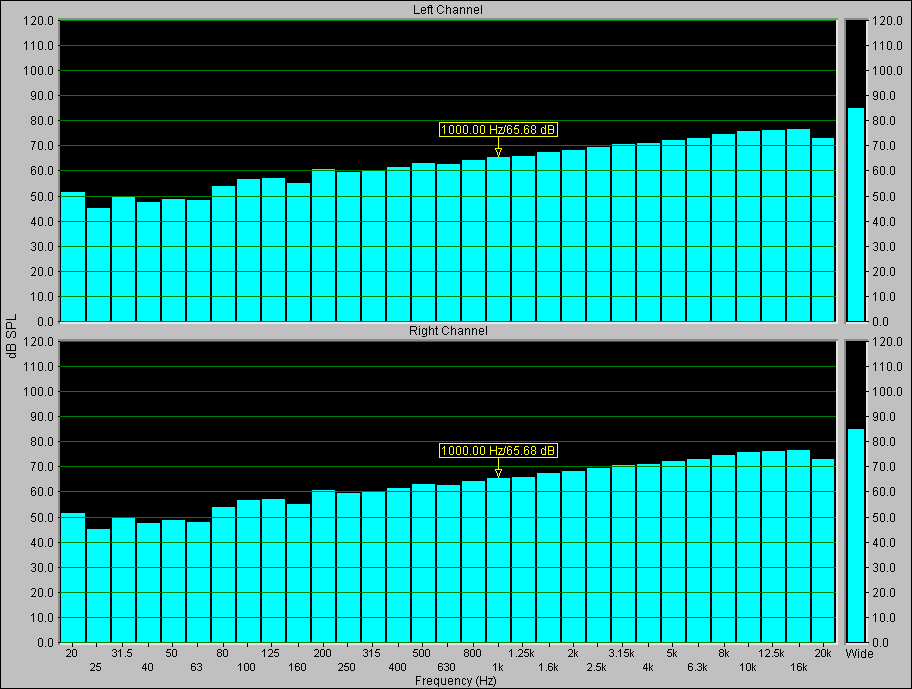
Fig. 7 - Rumore bianco visto in terzi d'ottava

Vediamo ora il rumore rosa:

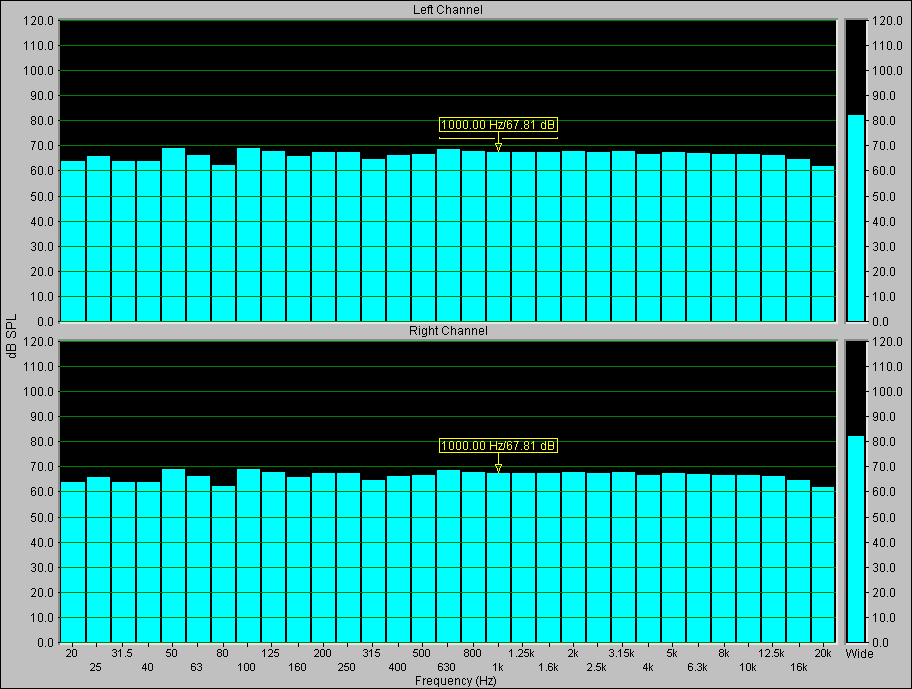
Fig. 8 - rumore rosa analizzato in terzi d'ottava

Si vede che lo spettro è pressoché piatto. Mediando con un tempo infinito si osserverebbe un ulteriore livellamento. Il fatto che non sia perfettamente piatto dipende dalla scheda audio del PC, che non è uno strumento professionale e spesso è di scarsa qualità.

Un'altra analisi che si può fare è il confronto tra lo stesso segnale ponderato A e lineare. Fino ad ora è stato sempre analizzato il segnale lineare, senza alcun tipo di filtraggio. La ponderazione A è un tipo di equalizzazione che esalta le frequenze maggiormente percepite dall'uomo e taglia quelle meno udibili (basse frequenze). Usiamo per questo scopo il segnale generato dalla voce umana, preso dal microfono collegato al computer. Specifichiamo che la barra a destra dello spettro, che rappresenta il segnale "totale" di quel canale, mostra il valore non ponderato. E' possibile anche avere il contrario.

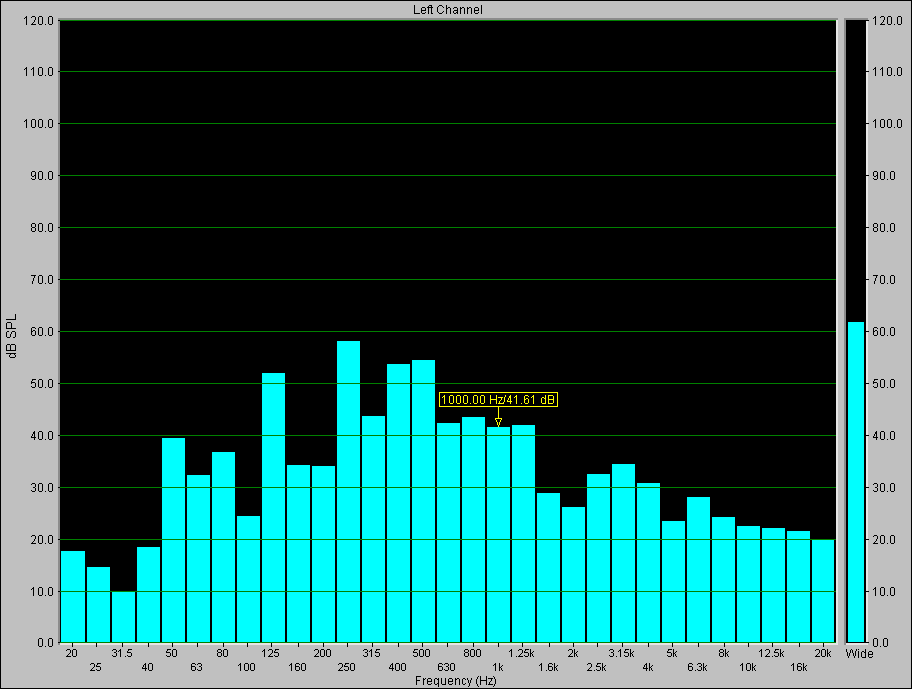
Fig. 9 - Segnale lineare (non ponderato A)

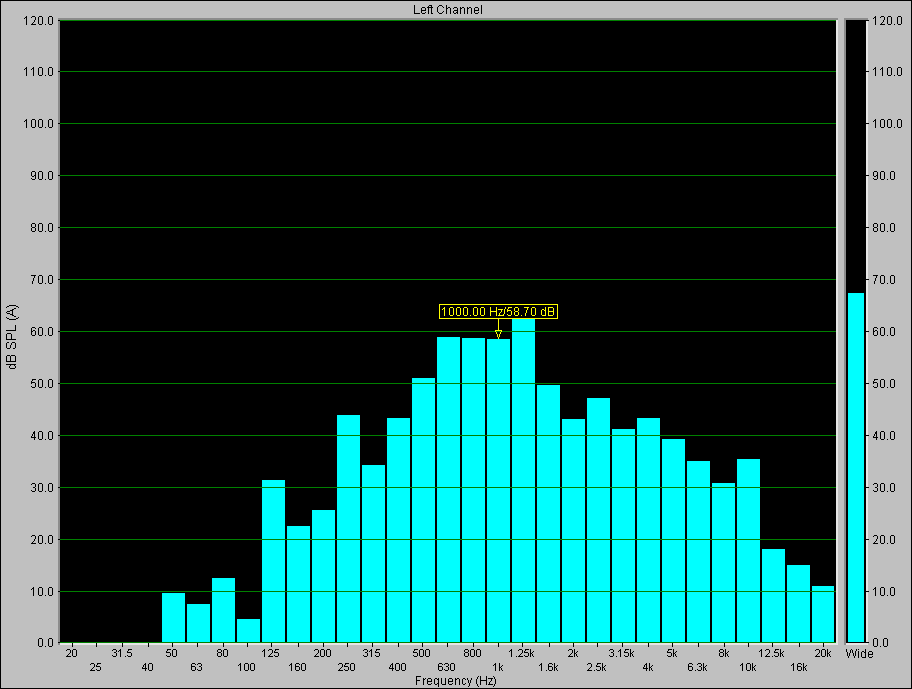
Fig. 10 - Stesso segnale ponderato A

In un caso come questo, cioè senza l'uso del fonometro, il segnale viene ponderato via software, anziché per via analogica come farebbe lo strumento. C'è chi contesta questo modo di eseguire la ponderazione, sostenendo che andrebbe sempre eseguita in modo analogico. In realtà, confrontando i due metodi, si vede che i risultati sono pressoché identici, a condizione ovviamente di utilizzare un buon software.

Un difetto comunque SpectraRTA lo ha: non è possibile visualizzare lo spettro minimo, come è richiesto dalla legge italiana. A tal proposito bisogna ricordare che la normativa del nostro paese è la più avanzata (decreto del 16 marzo 1998, consultabile all'indirizzo www.assoacustici.it), ma è di difficile attuazione a causa, almeno nei primi tempi, della mancanza di strumenti in grado di effettuare le misure richieste. Il caso dello spettro minimo ne è un esempio: a tutt'oggi i valori minimi si possono calcolare solamente utilizzando un software come Excel, e sfruttando la possibilità di copiarvi lo spettro di SpectraRTA sotto forma numerica. Ad esempio,

Fig.11 - es. di spettro in forma numerica come appare in Excel

I valori sopra riportati rappresentano lo spettro (fino a 500 Hz) di un segnale musicale: per ogni frequenza tra 20 Hz e 500 Hz (in terzi d'ottava) vengono riportati i valori in dB per il canale sinistro e destro. Come vedremo più avanti, attraverso Excel si può ampliamente elaborare il segnale.

Utilizziamo ora un altro programma, SpectraLAB. Questo software è un analizzatore in banda stretta (FFT) molto evoluto, con la possibilità di vedere anche la forma d'onda e lo spettro in terzi d'ottava. Il tutto in tempo reale, oltre naturalmente a molte altre funzioni.

Cominciando ad osservare in tempo reale la forma d'onda del segnale, ad esempio di un evento impulsivo (battito di mani, sparo di pistola ecc.), si vede che occorre abilitare il trigger, quella funzione grazie alla quale il programma comincia a visualizzare la forma d'onda, per ogni schermata, sempre a partire dallo stesso valore di ampiezza, ad es. al 15% del fondo scala, permettendo quindi un'analisi sullo schermo più agevole, poiché la forma del segnale e' fissa e non, come si avrebbe altrimenti, in movimento continuo.

Inoltre bisogna impostare anche un certo ritardo nella visualizzazione (delay) per fare in modo che la forma d'onda venga posta al centro dello schermo; ad es. 20 millisecondi.

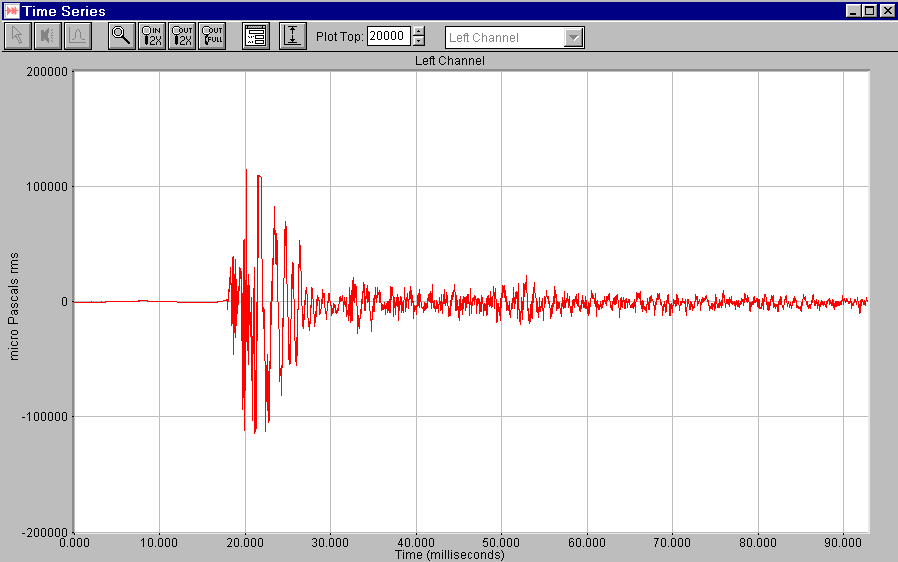
Fig. 12 - forma d'onda di un evento impulsivo (battito di mani)

SpectraLAB ci permetterà di verificare il fenomeno dell'aliasing: si va incontro a questo sgradevole "effetto collaterale" quando si campiona un segnale che contiene frequenze maggiori della metà di quella di campionamento. Per ottenere quindi un risultato corretto bisogna rispettare il teorema di Shannon, secondo il quale la frequenza di campionamento deve essere maggiore/uguale del doppio della frequenza massima contenuta nel segnale. ()

Per vedere l'aliasing occorre impostare correttamente SpectraLAB: cominciamo con un sampling rate di 44100 Hz e un decimation ratio pari a 1 (entrambi impostabili dal menu options à settings). Ora generiamo, attraverso l'apposita applicazione contenuta nel software, una frequency sweep, ossia un segnale che parte, nel nostro caso, da 100 Hz e arriva a 20000 Hz in un tempo di 10 secondi. Osservando lo spettro in tempo reale si può vedere la variazione della frequenza.

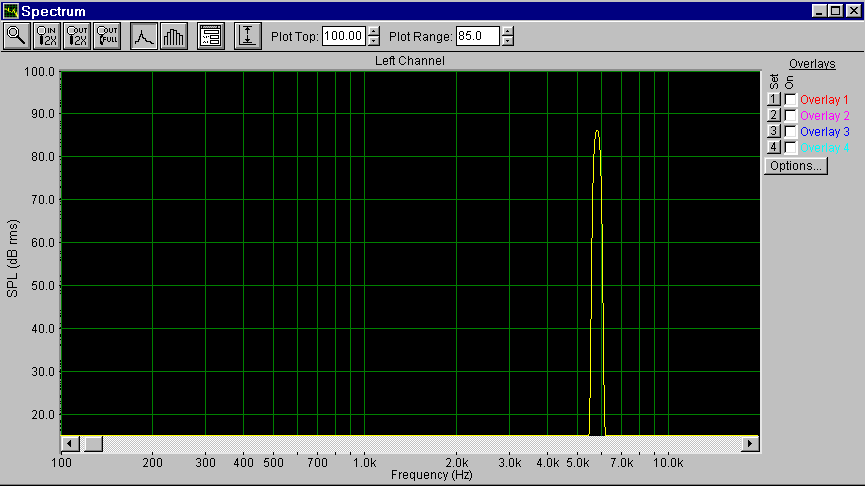
Fig. 13 - Spettro in FFT della frequency sweep a circa 6 KHz (no aliasing)

Per fare in modo che si verifichi l'aliasing impostiamo il decimation ratio a 4: in questo modo in pratica la frequenza di campionamento viene divisa per 8, e quindi possono essere analizzate correttamente frequenze non superiori a 5512,5 Hz .

Ricordiamo che con decimation ratio uguale a 1 la massima frequenza analizzabile è pari alla metà della frequenza di campionamento. Infatti, campionando ad es. 1 secondo a 44100 Hz si ottiene un numero di righe spettrali uguale alla metà della frequenza di campionamento, cioè 22050 Hz. La frequenza massima è detta frequenza di Nyquist, e l'intervallo in frequenza tra una riga spettrale e l'altra è dato dalla relazione

dove N = numero di campioni

Analizzando di nuovo il segnale in queste condizioni si vede che, dopo la frequenza massima consentita, si vede lo spettro che "torna indietro", ossia compaiono frequenze più basse: questo perché l'analisi FFT non viene più effettuata correttamente e il software "vede" frequenze più basse di quello che in realtà sono. Il segnale è sottocampionato. Le frequenze più alte di 5512,5 Hz vengono viste più basse di tale valore.

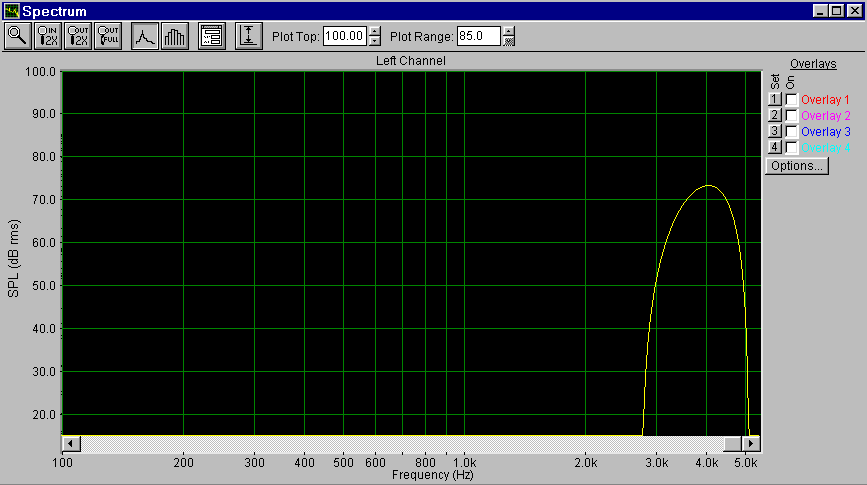
Fig. 14 - Spettro FFT che "torna indietro" oltre i 5 KHz

Per risolvere problema, registriamo con Cool Edit la frequency sweep per poi applicargli un filtro passa basso con frequenza di taglio a 5512 Hz. Riproducendo il segnale così modificato si vede scomparire il fenomeno dell'aliasing.

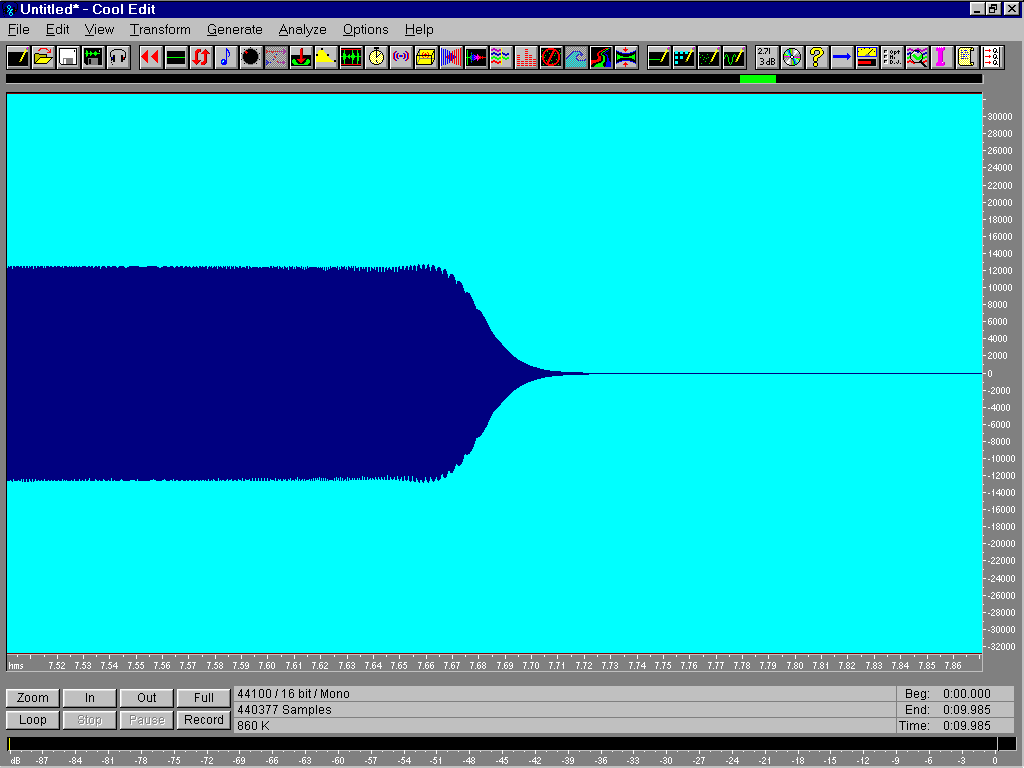
Fig. 15 - zona di taglio del filtro a 5512 Hz

Veniamo ora ad un altro tipo di misura, effettuabile solamente con il fonometro. Si tratta di registrare per un certo intervallo di tempo il livello equivalente sonoro () di ogni secondo di registrazione. Viene utilizzata la funzione data logging dello strumento. Questo tipo di misura è molto diversa da quella effettuata con il microfono ed il computer: mentre con quest'ultimo viene registrato il segnale vero e proprio, con il fonometro si acquisisce la storia temporale dei livelli sonori nel tempo. Nel primo caso posso riascoltare la registrazione, modificarla ecc. Nella seconda situazione si può solamente calcolare il livello equivalente complessivo, scaricando i dati sul computer e poi attraverso un software come Excel fare i calcoli necessari. Il fonometro viene usato in quei casi in cui l'utilizzo del PC sarebbe impossibile, come la registrazione del rumore da traffico per un'intera giornata. Il suono sotto forma digitale a 44100 Hz, 16 bit, stereo, occuperebbe una quantità di spazio su hard disk eccessiva. Restando in tema di misure effettuate con il fonometro, bisogna precisare che con questo strumento non si riescono a fare misure a norma di legge, a causa, come detto prima, della regolamentazione italiana, recente e molto avanzata. Infatti il fonometro:

• Non misura le costanti di tempo in simultanea
• Non fa l'analisi in frequenza in sesti d'ottava e con gli spettri min e fast
• Non misura per l'intera durata necessaria (16 ore per una misura diurna, 8 per una notturna)

Per questi motivi il 99% delle misure fatte in Italia non è a norma, ma con il passare del tempo probabilmente appariranno strumenti più avanzati in grado di soddisfare le richieste di legge.

Per scaricare i dati dal fonometro al computer si utilizza un collegamento via porta seriale e il programma di Windows 95 Hyperterminal, attraverso il quale è anche possibile comandare in remoto il fonometro. I valori, da salvare sotto forma di file di testo, contengono anche i livelli sonori percentili.

Dopo aver importato i dati in Excel, è possibile farne il grafico. Impostando correttamente l'asse delle ascisse (tempi) con gli orari delle rilevazioni e creando il grafico in formato X/Y si costruisce la traccia temporale dei livelli sonori.

Può essere utile calcolare il livello equivalente totale della misura. Calcolo la pressione al quadrato per ogni valore di che mi interessa (quindi fino ad una certa ora, visto che ad ogni minuto corrisponde un ):

Trovo la media aritmetica dei valori ottenuti:

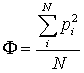
Ed infine trovo il livello quivalente totale:

Usando Excel è possibile creare una macro che esegua automaticamente questi calcoli. Inoltre, salvando lo spettro (in terzi d'ottava) di un segnale sotto forma numerica (attraverso Cool Edit, SpectraRTA o SpectraLAB) e importandolo in Excel, si può utilizzare quest'ultimo per l'elaborazione numerica del segnale. Un esempio classico è il l'applicazione della FFT sul segnale, grazie alla funzione incorporata nel programma. Graficando poi i risultati della FFT, si ottengono gli stessi risultati ottenibili con i software visti in precedenza. L'unico limite è il numero massimo di punti accettato da Excel , pari a circa 32000. Inoltre Excel produce lo spettro in frequenza che comprende anche la parte negativa. Si possono anche applicare filtri, semplicemente effettuando calcoli sullo spettro rappresentato in forma numerica.