![]()
(1)
Acustica
L’argomento di questa lezione è fornire la definizione delle principali grandezze che ricoprono un ruolo importante nel campo dell’acustica. Scopriremo che mentre alcune di loro sono già ben note e mantengono lo stesso significato al quale siamo abituati a pensare nel linguaggio corrente, ce ne sono altre che sono leggermente diverse, in particolare la pressione.
Suono
Il suono è una forma di trasporto di energia meccanica che avviene senza trasporto di materia mediante onde elastiche longitudinali in un mezzo, che può essere un gas, un liquido o un solido; (nel trasporto di calore convettivo si ha trasporto di materia) si ha trasporto di energia senza trasporto di materia, come per l’irraggiamento. Però mentre nell’irraggiamento l’energia è trasportata da un’onda elettromagnetica che non richiede l’esistenza di un mezzo, viceversa l’onda acustica porta energia tramite compressioni e rarefazioni di un mezzo. Nel vuoto quindi non si ha trasporto di energia acustica.
Esempio: la sveglia messa sotto una campana dove è fatto il vuoto. Man mano che si fa il vuoto il suono scompare. Si risente il suono quando si fa rientrare l’aria.
Tempo
Altre forme di energia hanno scale dei tempi per noi prive di importanza.
Per esempio, la luce o più in generale lo scambio termico per irraggiamento: il tempo che la luce impiega a riempire un locale è trascurabile. Non c’è transitorio. Viceversa nel campo acustico la scala dei tempi è fondamentale: il suono viaggia ad una velocità finita e piuttosto piccola: ci vuole del tempo affinché sia raggiunta la condizione di regime, anzi in realtà tale condizione non è mai raggiunta, si è sempre in transitorio. Per esempio, la voce in un ambiente non giunge mai in condizione di regime, è sempre in transitorio perché ogni sillaba è pronunciata in un tempo inferiore a quello che impiega una sorgente stazionaria ad andare a regime.
Tutti i fenomeni del suono li dobbiamo sempre rapportare al tempo. Il tempo lo misuriamo in secondi o millisecondi.
Potenza sonora P
La potenza sonora P (che si misura in W) è l’energia emessa da una sorgente nell’unità di tempo e dice quanto una sorgente è "forte".
Esempio
Per gli altoparlanti a colonnina, in genere si ha che:
Il rendimento h è:
|
(1) |
Intensità sonora I
L’intensità sonora I (che si misura in W/m²) rappresenta l’energia che fluisce nell’unità di tempo attraverso l’unità di superficie.
Supponiamo di avere una sorgente sonora S puntiforme ed omnidirezionale. L’intensità dipende dalla distanza e cala allontanandosi dalla sorgente.
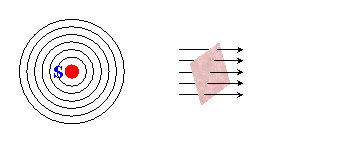
Figura 1 - L'intensità sonora di una sorgente puntiforme omnidirezionale dipende dalla distanza e cala allontanandosi da essa.
Ci sono tipi di sorgenti non puntiformi o non omnidirezionali per cui il calcolo dell’intensità non è così facile.
Velocità del suono
Ci sono in gioco due velocità: la velocità dell’onda sonora e la velocità delle particelle del mezzo. Consideriamo un lungo tubo di sezione circolare. Ad una estremità del tubo è presente uno stantuffo azionato da un albero che ruota a velocità angolare costante w. Il pistone si muoverà avanti ed indietro nel tubo con la legge del moto armonico, essendo la proiezione sull’asse x di un moto circolare uniforme.
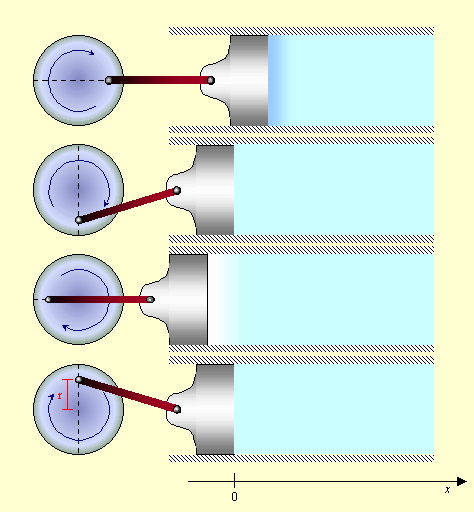
Figura 2 - Il moto del pistone nel tubo è armonico perché è la proiezione sull’asse x del moto uniforme di un punto, lungo una circonferenza di raggio r.
L’ampiezza del moto è:
|
(2) |
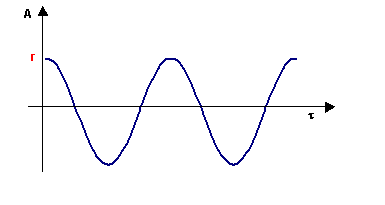
Figura 3 – Ampiezza del moto in funzione del tempo
L’aria immediatamente a contatto con la parete del pistone, per l’ipotesi di aderenza, segue il moto del pistone, si muove perciò alla stessa velocità, che si ottiene derivando A(t) rispetto al tempo:
|
(3) |
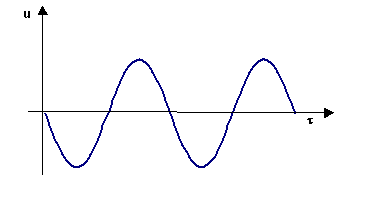
Figura 4 – Velocità delle particelle a diretto contatto con la parete del pistone in funzione del tempo
La velocità delle particelle ha valor medio nullo, perciò le particelle oscillano intorno ad una posizione di equilibrio, lungo l’asse x. Questo è vero per tutte le particelle, non solo per quelle che si trovano immediatamente a contatto con il pistone, poiché ogni strato d’aria funge da pistone per quello che lo segue.
Poiché ogni particella è dotata sia di massa che di elasticità, il mezzo non si comporta come un corpo rigido, cioè tutte le particelle non seguono immediatamente il pistone.
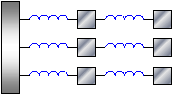
Figura 5 - Ogni particella può essere rappresentata da una massa (la sua inerzia) ed una molla (l'elasticità).
Imponendo una velocità al primo strato di particelle per mezzo del pistone, è necessario un certo lasso di tempo affinché questo funga da pistone per lo strato successivo. Il secondo strato, a sua volta, mette in movimento con un ulteriore ritardo lo strato successivo, e così via.
Invece, l'onda nel suo insieme si propaga con velocità finita come se l'aria fosse un corpo rigido. La perturbazione sonora viaggia lungo il tubo con la velocità del suono c (che si misura in m/s), che è diversa dalla velocità delle particelle.
La velocità del suono c non dipende dal particolare tipo di eccitazione, dalla sua ampiezza o frequenza. Essa è un'invariante rispetto alla legge del moto imposta all'aria (a differenza della velocità delle particelle) e dipende esclusivamente dalle proprietà termodinamiche del mezzo:
Nei gas perfetti è funzione solo della temperatura:
|
(4) |
In generale dipende anche dalla pressione:
|
(5) |
Nell'aria, a temperatura ambiente, c = 343 m/s a T=20°
Esempio
In un'aula di 17 m, la voce viaggia da un estremo all'altro in:
|
(6) |
Questo è il tempo impiegato dall'onda diretta (quella che compie il cammino più breve). La successiva riverberazione porta segnali che possono aver viaggiato nell'aria anche per mezzo secondo.
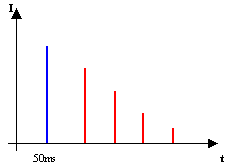
Figura 6 - In rosso è evidenziato il treno di impulsi dovuto alla riverberazione. L'intensità di questi impulsi cala perché percorrendo un cammino più lungo, sono assorbiti maggiormente.
Esistono altri fenomeni fisici di trasporto dell'energia meccanica in un mezzo che non godono della proprietà di avere la velocità di propagazione delle onde costante. Ad esempio le onde del mare viaggiano a velocità diverse a seconda della forma d'onda. In tal caso si parla di propagazione dispersiva.
Questo accade perché la propagazione sonora avviene tramite onde longitudinali), mentre la propagazione delle onde marine ha luogo tramite onde trasversali ( la velocità delle particelle è ortogonale a quella dell'onda).
In generale le onde trasversali sono dispersive, mentre quelle longitudinali o di compressione non lo sono.
Nei fluidi ideali, privi di viscosità, ha luogo esclusivamente la propagazione longitudinale in quanto non sono in grado di trasferire gli sforzi trasversali.
Nei fluidi reali, la viscosità permette il trasferimento di sforzi di taglio; in ogni caso è prevalente la propagazione tramite onde longitudinali: solo le onde marine sono trasversali perché si tratta di onde di interfaccia tra liquido e gas e non in un mezzo omogeneo.
Invece, in un materiale solido che reagisce agli sforzi taglianti, si può trasportare maggiore energia con onde trasversali che con onde longitudinali.
In un terremoto, parte dell'energia si propaga con onde longitudinali, parte tramite onde trasversali: i più devastanti sono quelli in cui predomina il contributo delle onde trasversali. Infatti poiché i treni d'onda di queste ultime viaggiano a velocità diverse, non arrivano contemporaneamente.
Cerchiamo la relazione che lega la velocità delle particelle a quella dell'onda. Per fare ciò bisogna definire la legge dello spostamento o la legge della velocità nello spazio.
Un punto a distanza x dalla parete del pistone si muoverà con legge del moto identica a quella di un qualsiasi punto a diretto contatto con il pistone, che è descritta dalle equazioni (2) e (3), ritardata net tempo. Il tempo di ritardo è quello necessario al suono, che viaggia con velocità c, per percorrere la distanza x:
|
(7) |
Legge del moto in qualsiasi punto del tubo
Fissato un istante di tempo tL , si sarà riempita di suono una lunghezza L di tubo pari a :
|
(8) |
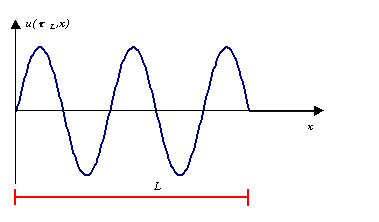
Figura 7 – Fissato tL, si è riempito di suono solo il tratto L di tubo
È più interessante valutare quanta parte di tubo si è riempita in un ciclo completo. Questa lunghezza prende il nome di lunghezza d'onda e si indica con l.
|
(9) |
È una misura in metri dello sviluppo spaziale di una completa oscillazione. Questa grandezza è facilmente definibile solo nel caso del moto armonico, quando la legge del moto è sinusoidale. Quindi la lunghezza d'onda è ben definita solo per i suoni puri, costituiti da una sinusoide a frequenza ben fissata.
Dobbiamo trovare il legame tra la lunghezza d'onda l e la velocità c:
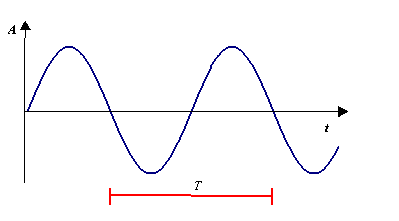
Figura 8
In un giro ci sono 2p radianti, allora:
|
(10) |
Poiché T è il tempo che impiega la manovella a fare un giro, il periodo T è l'inverso della frequenza f:
|
(11) |
Quindi, la relazione che lega lunghezza d'onda e velocità del suono è:
|
(12) |
Pressione sonora
Quando il pistone comprime l'aria, nelle vicinanze dello stesso, l'aria (che è un gas perfetto) diminuisce il suo volume
Consideriamo un elemento di volume che va da 0 a dx
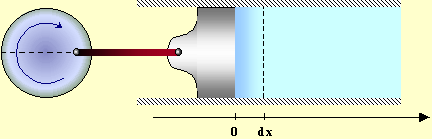
Figura 9
Mentre il pistone avanza, le particelle che si trovano ad una certa distanza dalla parete non si stanno ancora muovendo. Prima che inizino a muoversi deve trascorrere un intervallo di tempo pari a:
|
(13) |
Durante l'intervallo di tempo dt, il pistone si muove, ma l'aria a destra del volumetto di controllo è immobile, perciò varia il volume di quest’ultimo, e di conseguenza la pressione. In particolare durante le fasi in cui il pistone sta comprimendo l’aria, la pressione aumenterà. Una volta che il pistone ha terminato la sua corsa ed inizia a tornare indietro, l’aria continua a muoversi per inerzia verso destra e di conseguenza il volume aumenta ed la pressione diminuisce.
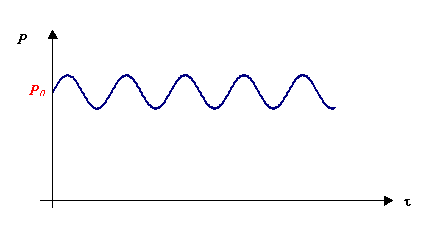
Figura 10 - La pressione fluttua con legge sinusoidale attorno alla pressione atmosferica
Chiameremo Pressione Sonora che indicheremo con Pi' (dove la "i" sta per istantanea e l'apice indica che è relativa), la differenza tra il valore locale istantaneo della pressione sonora P ed il valore medio della stessa P0:
|
(14) |
Osserviamo che la pressione sonora, essendo riferita a quella atmosferica, può assumere anche valori negativi come è facile intuire osservando la Figura 10.
Dal punto di vista del periodo o della lunghezza d’onda, l’onda di pressione è formalmente identica all’onda di velocità.
Nel caso particolare in esame, del suono all’interno di un tubo cilindrico a sezione costante che si propaga restando sempre uguale a se stesso, si ha il fenomeno di onda piana progressiva, nel quale P e u sono tra loro in fase.
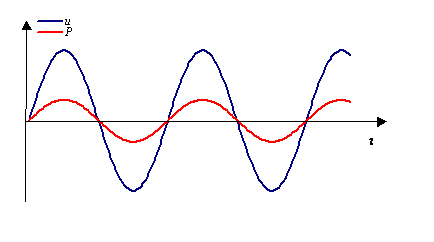
Figura 11 - Pressione e velocità delle particelle in funzione del tempo
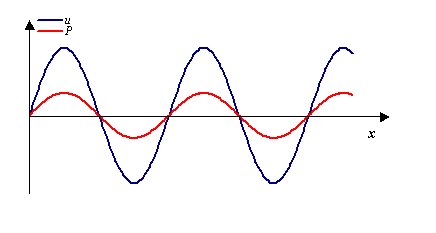
Figura 12 - Pressione e velocità delle particelle in funzione dello spazio
Se la sezione variasse, può succedere che queste due grandezze risultino sfasate; analogamente tensione e corrente in un circuito elettrico non sono sempre in fase.
Comunque se la pressione e la velocità delle particelle sono in fase, si ha il massimo trasferimento di energia; man mano che lo sfasamento cresce l’energia cala, fino al caso limite in cui la differenza di fase è pari a 90° in cui l’intensità diventa nulla.
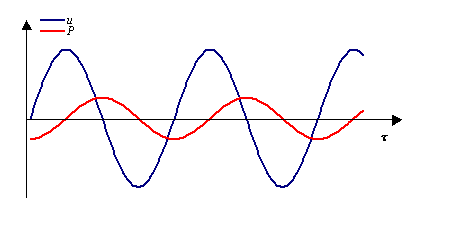
Figura 13 - Se pressione e velocità delle particelle sono in quadratura di fase, non si ha trasporto di energia e quindi propagazione del suono
Misura della pressione sonora
La valutazione e di conseguenza la misurazione della pressione sonora (ma anche della velocità delle particelle) è diventata possibile solo estremamente di recente: i convertitori analogico-digitali in grado di fornire una rappresentazione del segnale, istante per istante, hanno fatto la loro comparsa solo negli ultimi 10 anni.
Prima che ciò accadesse non era possibile misurare i valori istantanei di un qualunque segnale; era dunque necessario ricorrere ad una misura media.
Poiché il valore di una grandezza che oscilla attorno allo zero è zero, non si può ricorrere alla media lineare: è più corretto valutare la media efficace RMS (tale acronimo sta per Root Mean Square).
|
(15) |
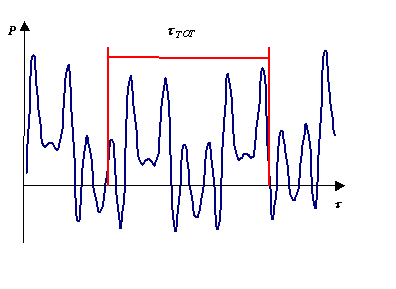
Figura 14 - tTOT è il tempo di integrazione
Questa è la media efficace lineare perché tutto il tempo di integrazione ha lo stesso peso. Questa è la definizione matematica esatta che è applicabile solo grazie alle strumentazioni moderne che prevedono il campionamento della forma d’onda: la potenza efficace si può calcolare per ogni singolo campione,
Poiché pero tutta l’acustica è stata sviluppata all’epoca in cui i sistemi di campionamento digitale non esistevano e si lavorava esclusivamente con sistemi analogici. Si riusciva quindi solo ad approssimare la risposta ideale di un mediatore a media mobile con un circuito RC.
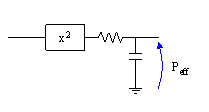
Figura 15 – Circuito RC per misurare la Potenza RMS
Tale circuito si comporta come un mediatore nel tempo, ma di tipo esponenziale e non lineare: ad ogni istante lo strumento risponde con un valor medio in cui ha più peso la storia recente.
|
(16) |
dove teff è uguale alla costante di tempo RC del circuito.
La risposta di un circuito RC tiene traccia di tutta la storia passata solo in teoria, perché in pratica dopo circa 10 teff la riduzione di ampiezza è così forte che si è persa ogni memoria del passato.
Sono state normalizzate due costanti di tempo RC standard chiamate:
costante SLOW = 1s
costante FAST = 0,125s
Tramite uno switch lo strumento di misura può commutare tra queste due costanti, pertanto con la costante SLOW la memoria complessiva è di 7-8 secondi; con costante FAST la memoria massima è di 1 secondo.
La risposta esponenziale con costante FAST è molto ben correlata con la percezione umana di intensità sonora: suoni più brevi della costante FAST tendono ad essere giudicati meno forti dal nostro sistema uditivo rispetto a suoni di lunghezza maggiore.
A questo punto bisogna legare la pressione sonora alla velocità delle particelle.
Questo può essere fatto in vari modi, ad esempio ricorrendo all’equazione di Navier del modo dei fluidi, togliendo il termine relativo alla viscosità, considerando quindi il fluido ideale.
Si possono fare ulteriori semplificazioni, come considerare il fenomeno adiabatico. Supponiamo che l’aria nel pistone (chiuso ad una estremità) si trovi in situazione di riposo, a pressione atmosferica p0 e volume specifico v0 corrispondente alla temperatura ambiente. Il pistone si muove comprimendo l’aria e se il sistema è termicamente isolato, possiamo considerare il fenomeno adiabatico perché immaginiamo che sia così rapido che le particelle non riescano a scambiare calore con quelle circostanti.
L’equazione che regola la trasformazione adiabatica è:
|
(17) |
dove
|
(18) |
Allora
|
(19) |
e derivando rispetto a r si ottiene:
|
(20) |
dove S resta costante poiché si ipotizza che la trasformazione sia reversibile e quindi isoentropica.
Valutiamo il valore in corrispondenza del punto di riposo, poiché ipotizzo piccole oscillazioni attorno al valore della pressione atmosferica.
|
(21) |
che si misura in [m2/s2]. Infatti tale valore è c2; quindi
|
(22) |
Perciò la velocità del suono, nei gas perfetti dipende solo dalla temperatura a cui si trova il gas in condizioni di equilibrio.
Per l’aria g =1,41 e R=0,287 allora:
c = 343 m/s a temperatura ambiente (T=193 °K)
Per i liquidi si ricava
|
(23) |
dove
|
(24) |
è il modulo di compressibilità isoterma ed è tabulato per vari liquidi in funzione della temperatura.
Nei solidi
|
(25) |
dove E è il modulo elastico [N/m2].
Tabella 1 – Valore della velocità del suono in vari mezzi
Mezzo |
Velocità del suono [m/s] |
Quarzo |
5486 |
Acciaio |
6096 |
Azoto (a 27°C e 1 BAR) |
355 |
Azoto (a 27°C e 100 BAR) |
379 |
Mercurio |
1451 |
Glicerina |
1895 |
Idrogeno |
1281 |
Elio |
600 |
Osserviamo che l’azoto non può essere considerato un gas perfetto perché la velocità del suono varia con la pressione.