
Corso semestrale di Fisica Tecnica

Docente del corso: professor Angelo Farina
Corso di laurea: Ingegneria elettronica
Università degli studi di Parma
Relazione della lezione di Fisica Tecnica n° 28
Lezione tenuta in data: 07/12/1998
Orario: 16.30 – 18.30
Oggetto: Il calcolo del coefficiente di convezione.

Autore della relazione: Gaetano Giulio Mongelli
Matricola: 97133
Il coefficiente di convezione
Vogliamo calcolare il coefficiente di convezione. Ricordiamo che nelle lezioni precedenti abbiamo definito il coefficiente di convezione con la seguente relazione
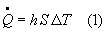
dove:
![]()
![]()
![]()
Se consideriamo l'unità di superficie, nella (1) ![]() rappresenta una sorta di coefficiente di proporzionalità tra
rappresenta una sorta di coefficiente di proporzionalità tra ![]() e
e ![]() : da questa considerazione
: da questa considerazione ![]() prende il nome di coefficiente di convezione .
prende il nome di coefficiente di convezione .
Facciamo tuttavia notare che nella tecnica la parola "coefficiente" è sinonimo di numero puro, mentre ![]() indicato nella (1) non è affatto un numero puro, ma è piuttosto una grandezza dimensionata.
indicato nella (1) non è affatto un numero puro, ma è piuttosto una grandezza dimensionata.
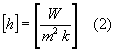
L’unità di misura di ![]() si esprime come indicato dalla (2) e dunque, a rigore, questo non è un coefficiente nel senso che abbiamo inteso di grandezza adimensionale. La nomenclatura che prevede l’utilizzo del termine "coefficiente" non è altro che uno di quei retaggi del passato, dei quali, purtroppo, la termotecnica è piena. A tal riguardo citiamo anche il caso della viscosità che su molti libri è chiamata coefficiente di viscosità sebbene non sia un coefficiente inteso nel senso di numero puro , adimensionale.
si esprime come indicato dalla (2) e dunque, a rigore, questo non è un coefficiente nel senso che abbiamo inteso di grandezza adimensionale. La nomenclatura che prevede l’utilizzo del termine "coefficiente" non è altro che uno di quei retaggi del passato, dei quali, purtroppo, la termotecnica è piena. A tal riguardo citiamo anche il caso della viscosità che su molti libri è chiamata coefficiente di viscosità sebbene non sia un coefficiente inteso nel senso di numero puro , adimensionale.
Ritornando al cosiddetto "coefficiente" di convezione, notiamo che ![]() non è neppure costante, ma dipende, come vedremo, da tutte le variabili dello scambio termico ed è dunque, a tutti gli effetti, una variabile, e non una costante numerica, come il termine "coefficiente" ci potrebbe fare presumere. Tuttavia è invalsa nel tempo la consuetudine di chiamarlo coefficiente e così faremo anche noi dal momento che se facessimo diversamente non ci intenderemmo più con il resto del mondo, pur avendo capito che questo è una grandezza dimensionata e , come tale, prevede un unità di misura.
non è neppure costante, ma dipende, come vedremo, da tutte le variabili dello scambio termico ed è dunque, a tutti gli effetti, una variabile, e non una costante numerica, come il termine "coefficiente" ci potrebbe fare presumere. Tuttavia è invalsa nel tempo la consuetudine di chiamarlo coefficiente e così faremo anche noi dal momento che se facessimo diversamente non ci intenderemmo più con il resto del mondo, pur avendo capito che questo è una grandezza dimensionata e , come tale, prevede un unità di misura.
Utilizzo della Teoria dei Modelli
Come si fa a calcolare operativamente il valore che assume il coefficiente di convezione ![]() ?
?
Si usa la cosiddetta teoria dei modelli alla quale avevamo già fatto cenno quando abbiamo trattato il moto dei fluidi nei condotti.
Ricordiamo che nel moto dei fluidi nei condotti, l’uso della teoria dei modelli aveva consentito di definire un unico numero puro (adimensionale) , chiamato numero di Reynolds che ci permetteva di classificare e correlare tra loro gli stessi fenomeni fisici che avvengono in tubi di diametro diverso, con fluidi diversi a densità diverse.
Avevamo scoperto in quel frangente che tutti i tubi che hanno la stessa geometria, lo stesso tipo di regime di moto (laminare o turbolento) e lo stesso numero di Reynolds danno luogo alle stesse perdite di carico anch’esse espresse in forma adimensionale dal fattore di attrito ![]() [leggi :"csi" ].
[leggi :"csi" ].
Sostanzialmente la teoria dei modelli è una struttura formale che permette la correlazione e l’utilizzo della stessa soluzione per problemi di tipo diverso. Infatti qualora in problemi di tipo diverso (ad esempio con geometria diversa) vengono rispettate delle condizioni chiamate condizioni di similitudine la teoria dei modelli fa corrispondere il risultato, che è, in forma adimensionale, lo stesso.
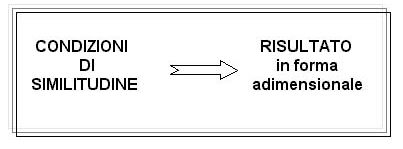
Figura 1 – schema applicativo della teoria dei modelli
Prime condizioni di similitudine : il numero di Reynolds e la similitudine geometrica
All’interno della problematica dello scambio termico per convezione , le prime condizioni di similitudine che devono essere rispettate sono per la prima parte quelle stesse che devono essere rispettate per il problema fluidodinamico. Tra le condizioni di similitudine troviamo allora il numero di Reynolds e un valore geometrico che descrive la geometria del problema.
Il numero di Reynolds
Nel caso del moto dei fluidi avevamo un’unica condizione di similitudine rappresentata dal numero di Reynolds (simbolo ![]() ) al quale corrispondeva un unico risultato rappresentato da:
) al quale corrispondeva un unico risultato rappresentato da:
1. il fattore di attrito ![]() se studiavamo il moto del fluido entro dei condotti
se studiavamo il moto del fluido entro dei condotti
2. il coefficiente ![]() (o
(o![]() , o
, o ![]() ) se studiavamo il moto dei fluidi liberi di scorrere
) se studiavamo il moto dei fluidi liberi di scorrere
Facendo riferimento al moto dei fluidi questo si traduce nel dire che se due problemi diversi hanno lo stesso numero di Reynolds avranno lo stesso valore del fattore di attrito ![]() . Allora l’applicazione della teoria dei modelli secondo il procedimento illustrato in figura 1 è molto semplice, e lo rappresentiamo di seguito in figura 2
. Allora l’applicazione della teoria dei modelli secondo il procedimento illustrato in figura 1 è molto semplice, e lo rappresentiamo di seguito in figura 2
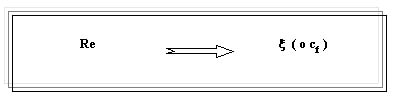
Figura 2 – corrispondenza condizioni di similitudine – risultato
nel caso del moto dei fluidi
Notiamo, per inciso, che ![]() e
e ![]() pur essendo stati storicamente sviluppati nell’ambito di due discipline scientifiche completamente diverse (dal momento che x
è derivato da studi di idraulica mentre il coefficiente
pur essendo stati storicamente sviluppati nell’ambito di due discipline scientifiche completamente diverse (dal momento che x
è derivato da studi di idraulica mentre il coefficiente ![]() è stato introdotto in aerodinamica) sono da considerarsi come grandezze adimensionali sostanzialmente simili. A conferma di questo, tra le due grandezze esiste la seguente relazione che non vogliamo dimostrare:
è stato introdotto in aerodinamica) sono da considerarsi come grandezze adimensionali sostanzialmente simili. A conferma di questo, tra le due grandezze esiste la seguente relazione che non vogliamo dimostrare:
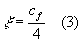
Vogliamo piuttosto sottolineare che la (3) è stata introdotta 50 anni dopo che le due grandezze erano state definite nell’ambito di due settori disciplinari molto lontani. Idraulica e aerodinamica vi sono stati presentati come argomenti della fluidodinamica , ma storicamente sono rami della tecnica dei quali si occupavano e si occupano scienziati e professionisti diversi che adoperano linguaggi e stili di risoluzione dei problemi diversi. Se infatti prendete in mano un libro di idraulica e lo confrontate con un libro di aerodinamica, aerotecnica o aeromodellismo sono in essi utilizzati linguaggi , notazioni, equazioni e simboli apparentemente diversi, poiché gli autori che li hanno scritti provengono da scuole scientifiche diverse. Tuttavia i libri in questione dicono le stesse cose poiché la fisica del moto dei fluidi che vi sta dietro è sempre la stessa.
Questa diversità di linguaggio ha comportato la definizione di due numeri puri che hanno lo stesso significato fisico, nei rispettivi campi e che differiscono fra loro di un fattore ![]() , il che nasconde l’idea dell’intrinseca descrizione dello stesso fenomeno.
, il che nasconde l’idea dell’intrinseca descrizione dello stesso fenomeno.
La similitudine geometrica
L’altra condizione di similitudine che entra nella fluidodinamica è la similitudine geometrica. Consideriamo problemi diversi con la stessa geometria, come ad esempio due tubi entrambi tondi, o due automobili di dimensioni diverse, ma con la stessa forma o aerei con la stessa forma in scale diverse.
Nel caso di tubi tondi si definiva un fattore di forma geometrico espresso dal rapporto adimensionale ![]() che avevamo indicato con il nome di scabrezza relativa.
che avevamo indicato con il nome di scabrezza relativa.
Anche questo rapporto rientra a buon diritto tra le condizioni di similitudine . Se il tubo tondo originale è liscio , il modello riprodotto in scala deve essere liscio perché i risultati sperimentali ottenuti lavorando sul modello si accordino perfettamente con quelli che si otterrebbero utilizzando il tubo originale. Se il tubo tondo è scabro, il modello e il prototipo, devono avere la stessa scabrezza relativa per dar luogo allo stesso fattore di attrito.
Quest’ultimo esempio ci aiuta a comprendere come il diagramma a blocchi illustrato in figura 1, il quale, dalle condizioni di similitudine, produce il risultato in forma adimensionale , non è limitato ad una sola condizione di similitudine e ad un solo risultato in forma adimensionale.
In generale ci possono essere ![]() condizioni di similitudine che producono
condizioni di similitudine che producono ![]() risultati in forma adimensionale con
risultati in forma adimensionale con ![]() e
e ![]() numeri grandi a piacere. Più complesso è il problema più grande sarà il numero delle condizioni di similitudine necessarie per definirlo e più grande sarà il numero delle variabili in uscita intese come risultato. Quindi, mentre nel moto dei fluidi abbiamo visto le cose da un punto di vista meno ampio, senza l’ausilio di una struttura formale, avendo ricavato alcuni risultati dal punto di vista intuitivo, ora che ci occupiamo del problema dello scambio termico in cui entrano in gioco molte più variabili, abbiamo bisogno di uno strumento potente che possa ampliare il nostro punto di vista per possedere in pieno il problema, e questo ci è permesso dall’introduzione di un potente strumento formale costituito dalla teoria dei modelli.
numeri grandi a piacere. Più complesso è il problema più grande sarà il numero delle condizioni di similitudine necessarie per definirlo e più grande sarà il numero delle variabili in uscita intese come risultato. Quindi, mentre nel moto dei fluidi abbiamo visto le cose da un punto di vista meno ampio, senza l’ausilio di una struttura formale, avendo ricavato alcuni risultati dal punto di vista intuitivo, ora che ci occupiamo del problema dello scambio termico in cui entrano in gioco molte più variabili, abbiamo bisogno di uno strumento potente che possa ampliare il nostro punto di vista per possedere in pieno il problema, e questo ci è permesso dall’introduzione di un potente strumento formale costituito dalla teoria dei modelli.
Quello che dobbiamo trovare per risolvere il problema di tipo termico, che è senz’altro uno dei più complessi, è un set di condizioni di similitudine che producono i risultati cercati. Le condizioni di similitudine ,come accadeva per il numero di Reynolds nel caso del problema fluidodinamico, sono, anche nel caso del problema dello scambio termico, espresse da una serie di numeri puri, cioè raggruppamenti adimensionali, che assumono il nome degli scienziati che li hanno introdotti. Tutte le volte che due problemi diversi avranno lo stesso valore di questi numeri puri in ingresso, troveremo in uscita lo stesso valore dei numeri puri risultato.
Altre due condizioni di similitudine: il numero di Grashof e il numero di Prandtl
In particolare all’interno della problematica dello scambio termico per convezione , le condizioni di similitudine, oltre a comprendere il numero di Reynolds e il numero ![]() (o un qualsiasi altro numero che descrive la geometria del problema) , comprendono anche due nuovi raggruppamenti adimensionali che sono il numero di Grashof ( simbolo Gr ) e il numero di Prandtl (simbolo Pr).
(o un qualsiasi altro numero che descrive la geometria del problema) , comprendono anche due nuovi raggruppamenti adimensionali che sono il numero di Grashof ( simbolo Gr ) e il numero di Prandtl (simbolo Pr).
Il numero di Grashof
Definiamo il numero di Grashof (simbolo ![]() ) con la relazione :
) con la relazione :
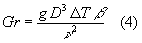
dove:
![]() è l’accelerazione di gravità
è l’accelerazione di gravità
![]()
![]()
![]()
![]()
Il numero di Grashof ha un significato fisico molto importante in quanto è indice del rapporto tra le forze di galleggiamento (rappresentate dal termine ![]() ) e le forze viscose. Dunque questo numero ci dice quanto il fluido tende a muoversi per effetto delle forze di galleggiamento che ricordiamo essere la causa della convezione naturale.
) e le forze viscose. Dunque questo numero ci dice quanto il fluido tende a muoversi per effetto delle forze di galleggiamento che ricordiamo essere la causa della convezione naturale.
Una delle interpretazioni del numero di Reynolds
Abbiamo appena accennato al fatto che il numero di Grashof è legato alla convezione naturale. Ci chiediamo a questo punto se è possibile dare un interpretazione simile per il numero di Reynolds. Ricordiamo l’espressione già nota del numero di Reynolds:
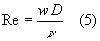
Dal momento che nella (5) compare esplicitamente l’espressione w della velocità del fluido, che è in generale una velocità imposta dall’esterno da una causa di moto, appare evidente che il numero di Reynolds è strettamente legato alla convezione forzata .
In generale il numero di Reynolds e il numero di Grashof esprimono le azioni forzanti del fenomeno: il primo esprime il legame con un’azione di tipo forzato dovuto alle forze esterne, che non ha nulla a che vedere con lo scambio termico; l’altro esprime il legame con un’azione di tipo naturale causata dallo scambio termico stesso.
Il numero di Prandtl
Infine l’ultimo raggruppamento adimensionale che fa parte delle condizioni di similitudine del problema dello scambio termico è il numero di Prandtl
Definiamo il numero di Prandtl (simbolo ![]() ) con la relazione :
) con la relazione :
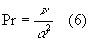
dove:
![]()
![]()
Abbiamo già notato nelle precedenti lezioni che ![]() e
e ![]() hanno la stessa unità di misura espressa in
hanno la stessa unità di misura espressa in ![]() e dunque il loro rapporto è un numero puro.
e dunque il loro rapporto è un numero puro.
Ricordiamo che quando avevamo studiato lo strato limite dinamico, il caso notevole della lastra piana orizzontale investita dal vento ci aveva permesso di fare alcune considerazioni sul significato fisico della viscosità cinematica ![]() . Analogamente, quando avevamo studiato lo strato limite termico, questo era stato lo spunto per fare delle considerazioni sul significato fisico della diffusività
. Analogamente, quando avevamo studiato lo strato limite termico, questo era stato lo spunto per fare delle considerazioni sul significato fisico della diffusività ![]() .
.
Il rapporto ![]() è sostanzialmente il rapporto tra la velocità di sviluppo dello strato limite dinamico e la velocità di sviluppo dello strato limite termico.
è sostanzialmente il rapporto tra la velocità di sviluppo dello strato limite dinamico e la velocità di sviluppo dello strato limite termico.
Quando un fluido investe un corpo come nell’esempio del vento che lambisce una lastra piana di taglio, si sviluppano contemporaneamente, da entrambi i lati della lastra piana uno strato limite dinamico e uno strato limite termico. In generale non è vero che lo strato limite dinamico coincida con lo strato limite termico, anzi quest'ultimo caso costituisce un caso limite molto particolare, che discuteremo.
Supponiamo di avere una lastra piana contro la quale soffia del vento con una certa temperatura ![]() e una certa velocità
e una certa velocità ![]() ,essendo la temperatura
,essendo la temperatura ![]() la temperatura del fluido vicino alla parete ed essendo la velocità del vento in prossimità della parete
la temperatura del fluido vicino alla parete ed essendo la velocità del vento in prossimità della parete ![]() , affinché venga rispettata l’ipotesi di aderenza.
, affinché venga rispettata l’ipotesi di aderenza.
Analizziamo per semplicità solo quello che succede da una parte della lastra, al di sopra della parete, tenendo presente che qualcosa di analogo succederà nella parte inferiore.
Dal punto di vista fluidodinamico si sviluppa uno strato limite dinamico all’interno del quale ricordiamo che il profilo della velocità ha un andamento sostanzialmente parabolico e la velocità ![]() che si ha in prossimità dello strato limite è per definizione di strato limite, il 99%
della velocità
che si ha in prossimità dello strato limite è per definizione di strato limite, il 99%
della velocità ![]() con cui soffia il vento lontano dalla lastra.
con cui soffia il vento lontano dalla lastra.
Nello stesso tempo, sempre dalla stessa parte della lastra si sviluppa anche uno strato limite termico che in generale avrà un profilo diverso dallo strato limite dinamico. Preso un certo punto lungo la lastra, la variazione di temperatura che si ha tra la temperatura ![]() del fluido in prossimità di un punto sulla lastra e la temperatura
del fluido in prossimità di un punto sulla lastra e la temperatura ![]() che si ha in prossimità dello strato limite termico equivale al 99%
della variazione di temperatura totale
che si ha in prossimità dello strato limite termico equivale al 99%
della variazione di temperatura totale ![]() .
.
In figura 3 è rappresentato il contemporaneo sviluppo dei due strati limite.
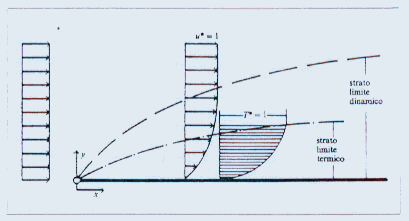
Figura 3 – Contemporaneo sviluppo degli strati limite dinamico e termico
Definiamo con la seguente relazione una variabile adimensionale della temperatura , che chiamiamo temperatura adimensionale e indichiamo con ![]() [leggi :"T star"] :
[leggi :"T star"] :
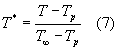
Andando a leggere i valori della temperatura adimensionale ![]() lungo l’asse y indicato in figura 3 , che rappresenta la direzione normale al piano della lastra , troviamo che , in prossimità dello strato limite termico, per definizione stessa di strato limite, la temperatura adimensionale
lungo l’asse y indicato in figura 3 , che rappresenta la direzione normale al piano della lastra , troviamo che , in prossimità dello strato limite termico, per definizione stessa di strato limite, la temperatura adimensionale ![]() vale:
vale: ![]() .
.
Allo stesso modo di quanto abbiamo fatto per la temperatura ,introduciamo una variabile adimensionale della velocità ![]() ,che chiamiamo velocità adimensionale e indichiamo con
,che chiamiamo velocità adimensionale e indichiamo con ![]() [leggi :" u star"]. Esprimiamo la velocità adimensionale
[leggi :" u star"]. Esprimiamo la velocità adimensionale ![]() con la seguente relazione:
con la seguente relazione:
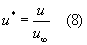
Andando a leggere anche i valori della velocità adimensionale ![]() lungo l`asse y , troviamo che in prossimità dello strato limite dinamico, per definizione stessa di strato limite, la velocità adimensionale
lungo l`asse y , troviamo che in prossimità dello strato limite dinamico, per definizione stessa di strato limite, la velocità adimensionale ![]() vale :
vale : ![]()
Abbiamo già accennato al fatto che in generale i due strati limite non coincidono. Allora comunque prenda un valore lungo l’asse x a cui corrisponde un punto sulla lastra , si ha in corrispondenza di tale punto una determinata altezza dello strato limite dinamico e un’altezza dello strato limite termico che sono in generale diverse.
Se accade che ![]() ovvero se
ovvero se ![]() abbiamo il caso particolare in cui lo strato limite dinamico coincide con lo strato limite termico.
abbiamo il caso particolare in cui lo strato limite dinamico coincide con lo strato limite termico.
Se accade che ![]() ovvero se
ovvero se ![]() abbiamo lo spessore dello strato limite termico è maggiore di quello dello strato limite dinamico. Questo è il fenomeno che si sviluppa tipicamente in aria dal momento che l’aria ha un numero di Prandtl pari a
abbiamo lo spessore dello strato limite termico è maggiore di quello dello strato limite dinamico. Questo è il fenomeno che si sviluppa tipicamente in aria dal momento che l’aria ha un numero di Prandtl pari a ![]() .Quando l’aria soffia contro un corpo lo strato limite dinamico che si sviluppa attorno a quel corpo è più sottile dello strato limite termico. Questo significa sostanzialmente che c’è una zona di fluido in moto che dal punto di vista fluido dinamico non avverte l’effetto frenante della parete, mentre dal punto di vista termico avverte lo scambio termico tra la parete e il fluido.
.Quando l’aria soffia contro un corpo lo strato limite dinamico che si sviluppa attorno a quel corpo è più sottile dello strato limite termico. Questo significa sostanzialmente che c’è una zona di fluido in moto che dal punto di vista fluido dinamico non avverte l’effetto frenante della parete, mentre dal punto di vista termico avverte lo scambio termico tra la parete e il fluido.
Se accade che ![]() ovvero se
ovvero se ![]() abbiamo il caso raffigurato in figura 3 sicché lo strato limite dinamico, proporzionale alla viscosità del mezzo n
, è più vivace e si sviluppa più rapidamente di quanto faccia lo strato limite termico, che è proporzionale alla diffusività
abbiamo il caso raffigurato in figura 3 sicché lo strato limite dinamico, proporzionale alla viscosità del mezzo n
, è più vivace e si sviluppa più rapidamente di quanto faccia lo strato limite termico, che è proporzionale alla diffusività ![]() . Questo è quello che accade tipicamente quando un corpo è investito dall’acqua, dal momento che l’acqua ha un numero di Prandtl variabile compreso tra
. Questo è quello che accade tipicamente quando un corpo è investito dall’acqua, dal momento che l’acqua ha un numero di Prandtl variabile compreso tra ![]() a seconda della temperatura dell’acqua dal momento che la viscosità dell’acqua cambia molto con la temperatura. Nell’acqua succede qualitativamente l’opposto di quanto succeda nell’aria : infatti c’è una zona di fluido in moto relativo rispetto alla parete che ne avverte l’effetto frenante dal punto di vista fluido dinamico e ancora non risente di una variazione di temperatura dovuta allo scambio termico.
a seconda della temperatura dell’acqua dal momento che la viscosità dell’acqua cambia molto con la temperatura. Nell’acqua succede qualitativamente l’opposto di quanto succeda nell’aria : infatti c’è una zona di fluido in moto relativo rispetto alla parete che ne avverte l’effetto frenante dal punto di vista fluido dinamico e ancora non risente di una variazione di temperatura dovuta allo scambio termico.
Problematica dello scambio termico
Per ogni set di dati in ingresso costituiti da queste quattro variabili si produce un risultato in uscita che è sempre lo stesso. Dunque il medesimo risultato in forma adimensionale vale per problemi diversi riguardanti lo scambio termico, ed è del tutto generale, purché le condizioni di similitudine siano rispettate dalle specifiche dei problemi che prendiamo in analisi.
Variabili in ingresso: condizioni di similitudine
Queste sono in generale le variabili di ingresso del problema dello scambio termico. Dunque sono quattro le condizioni di similitudine da rispettare perché in problemi differenti si possano ritenere validi gli stessi risultati e vogliamo qui ricordarle:
(devono essere soddisfatte le stesse condizioni di regime laminare o regime turbolento)
(deve essere verificata l'esistenza di un rapporto in scala tra modello e prototipo)
(deve essere verificata la condizione per cui il rapporto tra le forze di galleggiamento e le forze viscose sia lo stesso)
(deve essere verificata la condizione per cui si manifestino nello stesso modo lo sviluppo dello strato limite dinamico e dello strato limite termico)
Variabili in uscita: il risultato in forma adimensionale
Il risultato in uscita per il problema dello scambio termico è determinato da una coppia di valori adimensionali dove il primo valore è costituito dal fattore di attrito ![]() o dal coefficiente
o dal coefficiente ![]() , a seconda che ci si trovi nel caso di scambio termico con un fluido che viaggia entro un condotto, o con un fluido che è libero di viaggiare nello spazio, come abbiamo già visto prima. Il secondo valore è un parametro adimensionale molto importante nella problematica dello scambio termico dal momento che è strettamente legato al coefficiente di convezione, che è l'oggetto della nostra lezione, e questo è il numero di Nusselt.
, a seconda che ci si trovi nel caso di scambio termico con un fluido che viaggia entro un condotto, o con un fluido che è libero di viaggiare nello spazio, come abbiamo già visto prima. Il secondo valore è un parametro adimensionale molto importante nella problematica dello scambio termico dal momento che è strettamente legato al coefficiente di convezione, che è l'oggetto della nostra lezione, e questo è il numero di Nusselt.
Il numero di Nusselt
Il numero di Nusselt (simbolo ![]() )è espresso dalla relazione:
)è espresso dalla relazione:
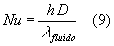
dove:
![]()
![]()
![]()
Notiamo allora che il numero di Nusselt altro non è che il coefficiente di convezione opportunamente adimensionalizzato.
E' ora possibile fare uno schema riassuntivo delle variabili di ingresso e di uscita del problema dello scambio termico applicando la teoria dei modelli. Tale schema è illustrato di seguito in figura 4.
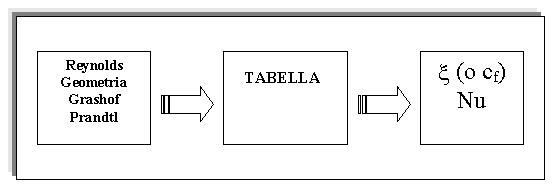
Figura 4 - Applicazione della teoria dei modelli al problema dello scambio termico
All'inizio della lezione ci siamo proposti di calcolare il coefficiente di convezione, ma abbiamo visto che il calcolo del coefficiente di convezione è strettamente legato al calcolo del numero di Nusselt. Procedendo a ritroso nelle nostre considerazioni abbiamo visto che il calcolo del numero di Nusselt è uno dei risultati in uscita di una operazione fatta da una certa "blackbox" di cui non conosciamo nulla per ora, a parte il fatto che questa richieda come variabili di ingresso quattro valori adimensionali che corrispondono alle condizioni di similitudine. Non abbiamo detto ancora nulla su questa "blackbox" ovvero su questa "scatola di elaborazione" dei dati di uscita, ma intuiamo che nel caso più semplice questa è costituita semplicemente da una tabella, ottenuta sperimentalmente, che in base a ogni possibile combinazione delle variabili di ingresso associa le variabili di uscita.
Guardando la figura 4 facciamo fatica a riconoscere una semplificazione introdotta dall'applicazione della teoria dei modelli, ma forse ci può far pensare il fatto che senza l'ausilio dell'analisi dimensionale e della teoria dei modelli il numero delle variabili in ingresso per il problema dello scambio termico non sarebbe quattro, ma almeno dodici o tredici tra le quali figurerebbero il tipo di fluido, la velocità, la temperatura, la densità, il calore specifico, la conducibilità,. Per riempire una tale sterminata tabella occorrerebbero tomi e tomi di carta, e sarebbero necessari millenni di esperimenti per elaborare tutti i possibili casi utili.
Il grande vantaggio introdotto dall'approccio del problema secondo la teoria dei modelli e l'analisi dimensionale, consiste nel fatto che scelta una geometria, e fatti variare in campi ragionevoli i valori dei numeri di Reynolds, Grashof e Prandtl a seconda della geometria, si è trovato un set ridotto di risultati attraverso i quali è possibile, interpolando, stabilire una formula generale da usare al posto della tabella. Queste formule (formulini) sono ottenute empiricamente e molto spesso esistono dei programmi (software) per P.C. che dato un insieme comunque sparpagliato di dati vi trova il formulino che li "fitta" meglio.
Dal momento che le tabelle poggiano su dati raccolti sperimentalmente, la loro storia è relativamente recente. Le prime ricerche e i primi esperimenti sono iniziati all'inizio del secolo scorso e possiamo ritenere che si siano concluse verso la fine degli anni trenta dal momento che i tedeschi prima dell'inizio della seconda guerra mondiale erano in possesso di tabelle e formulini per qualunque fenomeno di scambio termico, in qualunque geometria, con qualunque fluido.
Che poi questi dati fossero considerati come segreto militare, e in parte siano andati perduti durante il conflitto bellico, e si sia faticato nei decenni successivi per ricostruire queste informazioni, ciò non toglie negli anni tra il '39 e il '40 in questo campo non c'era sostanzialmente più niente da scoprire. Infatti i tedeschi di allora avevano fatto una quantità di esperimenti impressionante, con metodi avanzatissimi per l'epoca che prevedevano l'utilizzo di termocoppie con i dataloger per misurare la temperatura, quando nel mondo anglosassone si usavano ancora i termometri a mercurio. Gli scienziati tedeschi avevano raggiunto una conoscenza della relazione che lega il blocco dei dati di ingresso con quello dei dati di uscita per quanto riguarda lo scambio termico, che forse ancora non ripossediamo al giorno d'oggi.
Si rende allora necessaria, per arrivare al calcolo del coefficiente di convezione, la consultazione di tabelle reperibili su un manuale che riporti le diverse geometrie.
Data una certa geometria, ad esempio un tubo, ci sono tabelle che mi danno il numero di Nusselt in funzione del numero di Reynolds e del numero di Prandtl .
Facciamo ora un esempio pratico:
Problema
Consideriamo dell'acqua che scorre in un tubo di diametro D di 0.05 m (50 mm). La temperatura di parete del tubo sia costante e pari a ![]() , mentre la temperatura dell'acqua sia pari a
, mentre la temperatura dell'acqua sia pari a ![]() e dunque vi sia una differenza di temperatura tra la parete del tubo e il fluido in moto di 90°
C. Sia la velocità
e dunque vi sia una differenza di temperatura tra la parete del tubo e il fluido in moto di 90°
C. Sia la velocità ![]() dell'acqua di 2 m/s . Trovare il coefficiente di convezione
dell'acqua di 2 m/s . Trovare il coefficiente di convezione![]() .
.
Figura 5 - Tubo in cui scorre l'acqua
I dati del problema sono:
![]()
![]()
![]()
![]()
![]()
![]()
La geometria del problema è fissata: si tratta di un tubo liscio. Per risolvere il problema dobbiamo calcolare i valori in ingresso del numero di Reynolds, Grashof e Prandtl dal momento che la geometria è fissata. Per avere i valori di questi numeri bisogna ottenere alcuni dati sperimentali dalle tabelle.
Cominciamo dal numero di Reynolds. Sostituendo i valori numerici nella (5) abbiamo che:
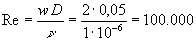
Siamo dunque in regime turbolento.
Se ora consulto un libro per vedere cosa succede in regime turbolento per dell'acqua che viene scaldata dentro un condotto circolare, in convezione forzata trovo un formulino che riguarda il caso in esame. Questo è il formulino di Dittus e Boelter che prende il nome dagli omonimi scienziati ed è molto utilizzato. Viene espresso con la relazione:
![]()
E il numero di Grashof è sparito?
In realtà Grashof è elevato alla zero e non compare in questo caso, dal momento che ci troviamo in una situazione di convezione forzata e la trattazione del problema tramite il formulino di Dittus e Boelter ci dice di trascurare proprio quel termine che abbiamo considerato sopra come indice della convezione naturale. Può essere utile esprimere la (10.1) in modo più dettagliato con l'espressione:
![]()
Consultiamo ora il valore del numero di Prandtl dell'acqua che è funzione della temperatura. A noi interessa l'intervallo compreso tra i 10°C e i 100°Ce dovremo scegliere una temperatura media in cui considerare il valore di tale numero
|
Temperatura in°C |
0 |
25 |
50 |
75 |
100 |
|
Prandtl Per l'acqua |
13,7 |
6,1 |
3,57 |
2,23 |
1,76 |
Tabella 1 Dipendenza del numero di Prandtl dell'acqua dalla temperatura
L'acqua è un mezzo il cui numero di Prandtl varia molto con la temperatura e nel nostro problema c'è un bel salto di temperatura poiché passiamo da 10°C dell'acqua ai 100°C della parete del tubo. Assumiamo come valore del numero di Prandtl per l'acqua il valore relativo alla temperatura di 50°C, poiché è quello che più si approssima al valore relativo alla temperatura di 55°C (ottenuta come media tra 10°C e 90°C). Allora il numero di Prandtl vale approssimativamente 3,57, ma fortunatamente, secondo il formulino di Dittus e Boelter questo numero va elevato a un esponente piuttosto piccolo (0,4) di modo che l'errore che si commette approssimando il numero di Prandtl viene contenuto e non influisce molto sul calcolo del numero di Nusselt.
Sostituendo i valori numerici nella (10.1) ottengo :
![]()
Avendo Nusselt posso ricavare il coefficiente di convezione h sostituendo i valori numerici nella (9) :
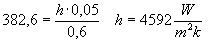
Il valore di h è abbastanza alto, ciò è indice di uno scambio termico vivace.
Perfezioniamo ulteriormente il nostro esempio:
Prendiamo un tubo lungo ![]() e vogliamo trovare la temperatura di uscita
e vogliamo trovare la temperatura di uscita ![]()
I dati aggiuntivi del problema sono:
![]()
![]()
![]()
Abbiamo detto che la temperatura dell'acqua all'ingresso del tubo era 10°C. La temperatura dell'acqua all'uscita del tubo sarà senz'altro più alta perché il fluido ha ricevuto calore dalla parete del tubo mantenuto alla temperatura costante di 100°C.
Quanto calore ha ricevuto il fluido complessivamente dal tubo?
Conoscendo il coefficiente di convezione h è facile calcolare la potenza termica che il fluido ha ricevuto sostituendo i valori numerici nella (1):
![]()
Il fluido riceve una potenza pari a circa 324 kW che è una potenza considerevole ed è responsabile dell'aumento di temperatura dello stesso. Il legame tra la potenza ricevuta e il conseguente aumento di temperatura, si ottiene in questo caso dall'equazione del primo principio per un sistema aperto, scritta tra la sezione di ingresso e la sezione di uscita del tubo. Dall'espressione di primo principio abbiamo:
![]()
dove:
![]()
![]()
Ma il salto di entalpia dell'acqua lo posso esprimere in funzione del salto di temperatura tra il fluido all'uscita e il fluido all'ingresso con la relazione:
![]()
Vogliamo far notare che il![]() non va confuso con la differenza di temperatura
non va confuso con la differenza di temperatura ![]() tra la temperatura di parete e quella del fluido, ma riguarda esclusivamente la temperatura di ingresso e la temperatura di uscita del fluido.
tra la temperatura di parete e quella del fluido, ma riguarda esclusivamente la temperatura di ingresso e la temperatura di uscita del fluido.
Facciamo un disegno per capire meglio:
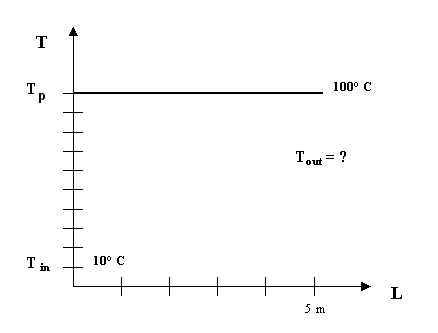
Figura 6 - impostazione del problema della variazione della temperatura del fluido
A priori , non conosciamo la legge con cui varia la temperatura del fluido che scorre nel tubo , né conosciamo la temperatura all'uscita del tubo. Conosciamo solo la temperatura di ingresso dell'acqua nel tubo a 10°C. Nel disegno è indicata anche la temperatura di parete del tubo che rimane costante a 100 °C.
Il fluido entra a ![]() si scalda ed esce con una certa
si scalda ed esce con una certa ![]() .
.
A rigore il ![]() che compare nella ( 1 ) è la differenza tra la temperatura di parete
che compare nella ( 1 ) è la differenza tra la temperatura di parete ![]() e quella del fluido che si sta scaldando e varia con la legge di variazione della temperatura del fluido che ancora non conosciamo.
e quella del fluido che si sta scaldando e varia con la legge di variazione della temperatura del fluido che ancora non conosciamo.
Nel calcolo che abbiamo fatto prima ,abbiamo assunto in prima approssimazione che![]() il che è corretto solo nella misura in cui il valore
il che è corretto solo nella misura in cui il valore ![]() del fluido all’uscita del tubo non si discosti troppo dal valore
del fluido all’uscita del tubo non si discosti troppo dal valore ![]() del fluido all’ingresso . Tuttavia noi non conosciamo a priori di quanto varia la temperatura del fluido all’uscita del tubo rispetto a quella che si ha all’ingresso del tubo, ed è ciò che valuteremo. Se troviamo un valore di
del fluido all’ingresso . Tuttavia noi non conosciamo a priori di quanto varia la temperatura del fluido all’uscita del tubo rispetto a quella che si ha all’ingresso del tubo, ed è ciò che valuteremo. Se troviamo un valore di ![]() che si discosta troppo da
che si discosta troppo da ![]() dovremo tenere conto che la differenza di temperatura tra parete e fluido non è costante, ma varia man mano che il fluido percorre il tubo.
dovremo tenere conto che la differenza di temperatura tra parete e fluido non è costante, ma varia man mano che il fluido percorre il tubo.
Troviamo il valore della portata in massa ![]() con la relazione:
con la relazione:
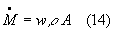
dove:
![]()
![]()
![]()
Sostituendo i valori numerici nella ( 14 ) si ha :
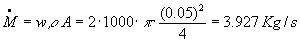
Possiamo ricavare la temperatura ![]() dalla ( 13 ) sostituendo il valore della portata in massa appena calcolato e avremo che:
dalla ( 13 ) sostituendo il valore della portata in massa appena calcolato e avremo che:
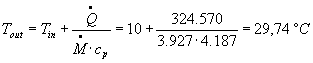
A questo punto abbiamo ottenuto un'informazione utile, comunque approssimata, per quanto riguarda la temperatura del fluido all'uscita del tubo, e possiamo tracciare, non senza un certo margine di errore, l’andamento della temperatura del fluido che percorre il tubo, completando il grafico di figura 6.
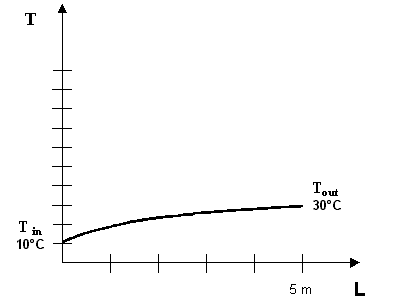
Figura 7 - andamento della temperatura del fluido che scorre nel tubo
Il fluido entra a una![]() = 10 °C ed esce a una
= 10 °C ed esce a una ![]() = 29.74 °C che possiamo arrotondare per semplicità a
= 29.74 °C che possiamo arrotondare per semplicità a ![]() =30 °C. Osservo che la
=30 °C. Osservo che la ![]() tra la parete del tubo e il fluido che vi scorre non è più costante, poiché mentre la temperatura di parete è rimasta sempre a 100°C, mentre la temperatura del fluido è variata da
tra la parete del tubo e il fluido che vi scorre non è più costante, poiché mentre la temperatura di parete è rimasta sempre a 100°C, mentre la temperatura del fluido è variata da![]() a
a ![]() .
.
Possiamo migliorare ulteriormente il risultato cercato sostituendo al valore del ![]() iniziale un più opportuno
iniziale un più opportuno ![]() medio tra il
medio tra il ![]() iniziale di 90 °C e il
iniziale di 90 °C e il ![]() finale di 70 °C. Con una precisione migliore della precedente, posso ripetere il calcolo con
finale di 70 °C. Con una precisione migliore della precedente, posso ripetere il calcolo con ![]() .
.
Il risultato di questo calcolo, così come il procedimento stesso, è comunque approssimato, e se volessi procedere più correttamente, dovrei dividere il tubo in tanti tubi più corti e ripetere il calcolo fatto sopra per ogni singolo tubo, poiché in ciascuno di essi anche il coefficiente di convezione sta cambiando. Sostituendo ![]() al
al ![]() iniziale otteniamo un valore certamente meno errato, ma restiamo sempre nell’ordine di grandezza dei calcoli inesatti, poiché osserviamo che man mano che le proprietà del mezzo variano con la temperatura , cambia il numero di Reynolds, cambia il numero di Prandtl, quindi a seconda del tratto di tubo che considero trovo un numero di Nusselt diverso e quindi cambia la dinamica dello scambio termico, con tutto il set dei valori di ingresso a cui è legato. Comprendiamo allora l'approssimazione che si verifica qualora manteniamo costante il valore del coefficiente di convezione
iniziale otteniamo un valore certamente meno errato, ma restiamo sempre nell’ordine di grandezza dei calcoli inesatti, poiché osserviamo che man mano che le proprietà del mezzo variano con la temperatura , cambia il numero di Reynolds, cambia il numero di Prandtl, quindi a seconda del tratto di tubo che considero trovo un numero di Nusselt diverso e quindi cambia la dinamica dello scambio termico, con tutto il set dei valori di ingresso a cui è legato. Comprendiamo allora l'approssimazione che si verifica qualora manteniamo costante il valore del coefficiente di convezione ![]() su tutto il tubo , e variamo solamente il
su tutto il tubo , e variamo solamente il ![]() . Qui è questione di stabilire qual è il nostro obiettivo di precisione e fino a che punto dobbiamo continuare a raffinare il calcolo, poiché il formulino di Dittus e Boelter fornisce dei risultati con un margine di errore del 20-30% .
. Qui è questione di stabilire qual è il nostro obiettivo di precisione e fino a che punto dobbiamo continuare a raffinare il calcolo, poiché il formulino di Dittus e Boelter fornisce dei risultati con un margine di errore del 20-30% .
Tornando al problema, andiamo a sostituire nella (1) ![]() anziché
anziché ![]() e calcoliamo nuovamente la potenza con:
e calcoliamo nuovamente la potenza con:
![]()
La potenza totale scambiata è scesa da 324 KW a 288 KW. Otterremo un nuovo valore di Tout se sostituiamo questo valore numerico nella seguente espressione :
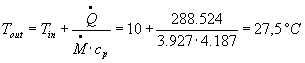
Ora ci si potrebbe chiedere se sia necessario precisare ulteriormente il calcolo prendendo un ![]() ma facciamo notare come questo ennesimo raffinamento del calcolo sia inutile in quanto non ha senso iterare il procedimento fino a più cifre decimali della variabile
ma facciamo notare come questo ennesimo raffinamento del calcolo sia inutile in quanto non ha senso iterare il procedimento fino a più cifre decimali della variabile ![]() quando dovremmo essere più precisi su ben altre variabili quali il numero di Reynolds, il numero di Prandtl e il numero di Nusselt, che per effetto della variazione di temperatura del fluido sono cambiati parecchio.
quando dovremmo essere più precisi su ben altre variabili quali il numero di Reynolds, il numero di Prandtl e il numero di Nusselt, che per effetto della variazione di temperatura del fluido sono cambiati parecchio.
Se volessimo un calcolo davvero più raffinato, l'unica procedura corretta sarebbe quella di suddividere il tubo lungo in tanti pezzi di tubo più corto e per ciascun pezzo di tubo fare un calcolo della temperatura di uscita del fluido, che serve come dato di ingresso per il calcolo della ![]() del tubo successivo. Suddividendo il tubo del problema , lungo 5 m , in tanti tubi più piccoli lunghi 1 m , e ripetendo l'operazione sopra descritta per ciascuno di essi, si arriva alla
del tubo successivo. Suddividendo il tubo del problema , lungo 5 m , in tanti tubi più piccoli lunghi 1 m , e ripetendo l'operazione sopra descritta per ciascuno di essi, si arriva alla ![]() dell'ultimo tubo che coincide con la stima della
dell'ultimo tubo che coincide con la stima della ![]() finale.
finale.
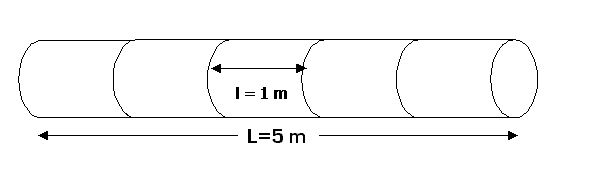
Figura 8 - suddivisione del tubo in cinque elementi più piccoli
Probabilmente così , l'errore commesso è minore di quello commesso nel calcolo fatto prima. Abbiamo detto "probabilmente" dal momento che ciascuno di questi cinque calcoli è poi affetto da un errore congenito del 20-30% dovuto all'uso della formula di Dittus e Boelter. Dunque è sbagliato credere che dividendo e spezzettando il calcolo in tanti calcoli effettuati su porzioni più piccole si riesca sempre ad aumentare la precisione del risultato finale. In generale questo non è vero, poiché se il metodo di calcolo è comunque affetto da errori, voi potete spezzettare il problema finchè volete e pervenire a tanti risultati parziali affetti da errore, con l'effetto che il risultato finale sarà comunque affetto di errore.
Questo è un concetto che purtroppo nel calcolo numerico non viene spiegato a sufficienza e normalmente lo studente crede erroneamente che facendo una serie di raffinamenti e suddivisioni e facendo fare al calcolatore milioni di calcoli, per giorni e giorni, il risultato, alla fine, diventi più preciso. Non è così. Anzi va anche peggio, perché se il metodo che sta alla base del calcolo ha delle vacuità, addirittura facendo accumulare gli errori di calcolo potete trovare un risultato il cui errore cresce, tanto più fate raffinare la cosa. Se voi stimate ogni temperatura a partire da quella precedente voi capite che l'errore di stima compiuto sulla prima, causa un ulteriore errore di stima sulla seconda, e così via per tutte le parti in cui abbiamo suddiviso il sistema. Questo è un errore di tipo cumulativo, ed è ad ogni passo figlio dell'errore precedente. La somma degli errori cumulativi, per discretizzazioni di centinaia, migliaia di incognite può diventare molto più grande dell'errore di stima fatto facendo una simulazione in blocco dall'inizio alla fine del tubo, dove sapevo che comunque più del 20-30% la formula di Dittus e Boelter non ha mai sbagliato, mentre non c'è limite al peggio.
A forza di fare degli errori piccolini e cumulativi voi potete ottenere un risultato che raccoglie tali errori di modo che commettete un errore del 3000% con la massima facilità. Gli stessi scienziati che si occupano di calcolo numerico, che però non sono ingegneri , e quindi non costruiscono gli apparecchi, non si accorgono di questo fatto. Si vendono programmi bellissimi di calcolo agli elementi finiti in cui i relativi manuali suggeriscono erroneamente di raffinare sempre più, per far comprare il computer più potente o l'ultima versione del programma che gestisce più elementi , facendo credere all'utente di avere un risultato più preciso e così non è. Dunque il vecchio metodo basato sull'analisi dimensionale col formulino che trovate su qualunque libro fa un errore, ma che sapete quantificare e vi consente una rapida stima del coefficiente di convezione, che è normalmente l'incognita più difficile da definire con precisione in un problema di scambio termico. Infatti sulla parte conduttiva il calcolo può essere abbastanza preciso anche con calcoli numerici, mentre sulla parte convettiva il calcolo è sempre impreciso.
Metodo per ricavare l'espressione del numero di Nusselt
Adesso vogliamo capire come si ricava l'espressione (9) con la quale abbiamo introdotto il numero di Nusselt. Il trucco per ottenere questa espressione consiste nell'adimensionalizzazione della condizione al contorno termico.
Consideriamo il caso di un fluido che investe una parete piana a temperatura diversa da quella del fluido stesso. Ricordiamo che quando ho una parete che si trova alla temperatura ![]() e ho un fluido che si trova alla temperatura
e ho un fluido che si trova alla temperatura ![]() che investe la parete, la temperatura del fluido varia in prossimità della parete in questo modo:
che investe la parete, la temperatura del fluido varia in prossimità della parete in questo modo:
- a una certa distanza, lontano dalla parete l'effetto della parete non si sente più e la temperatura del fluido è pari alla temperatura![]() del fluido imperturbato.
del fluido imperturbato.
- man mano che mi avvicino alla parete raggiungo lo strato limite termico dove per definizione ho il 99% della variazione totale tra la temperatura di parete e quella del fluido
- tra lo strato limite e la parete ho un forte gradiente di temperatura fino a che raggiungo la temperatura![]() di parete.
di parete.
Abbiamo già definito con l'espressione (7) la temperatura adimensionale![]() come:
come:
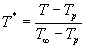
La temperatura adimensionale vale ![]() alla parete e vale
alla parete e vale ![]() a distanza infinita dalla parete che interagisce con il fluido in moto. Abbiamo visto che la temperatura adimensionale
a distanza infinita dalla parete che interagisce con il fluido in moto. Abbiamo visto che la temperatura adimensionale ![]() è una variabile che varia tra 0 e 1.
è una variabile che varia tra 0 e 1.
Per la trattazione che vogliamo fare non ci interessa che il fluido sia in moto dovuto a convezione forzata o convezione naturale dal momento che noi andremo ad indagare unicamente ciò che succede sul primo strato atomico di fluido a contatto con la parete stessa. Nel primo strato infinitesimo a contatto con la parete considero la velocità del fluido nulla poiché resta valida l'ipotesi di aderenza. Possiamo scrivere che la quantità di calore scambiata tra il fluido immobile e la parete nella zona di contatto per unità di tempo e per unità si superficie è data dalla legge di Fourier che avevamo trovato per la conduzione:
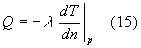
dove ![]() è la grandezza scalare che abbiamo denominato coefficiente di conduttività termica o più semplicemente conducibilità.
è la grandezza scalare che abbiamo denominato coefficiente di conduttività termica o più semplicemente conducibilità.
Tuttavia è valida, più in generale, l'espressione (1) che per unità di tempo e di superficie possiamo riscrivere come:
![]()
Unendo allora la (15) con la (16) abbiamo che:
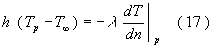
Per ricavare l'espressione del numero di Nusselt dobbiamo adimensionalizzare questa equazione. Per adimensionalizzare questa equazione, oltre a creare una variabile adimensionale della temperatura che abbiamo chiamato temperatura adimensionale ![]() , indicata nella (8), dobbiamo creare una variabile adimensionale anche per la direzione normale che chiameremo normale adimensionale
, indicata nella (8), dobbiamo creare una variabile adimensionale anche per la direzione normale che chiameremo normale adimensionale ![]() . Per fare questo scegliamo un asse
. Per fare questo scegliamo un asse ![]() normale alla superficie di contatto tra parete e fluido e lo dividiamo per la lunghezza caratteristica
normale alla superficie di contatto tra parete e fluido e lo dividiamo per la lunghezza caratteristica ![]() .
.
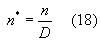
Nel caso in analisi abbiamo una parete piana, e si potrebbe obbiettare che non è facile dire a priori quale sia la lunghezza caratteristica ![]() di una parete piana. Tuttavia osserviamo che il procedimento che stiamo seguendo ora è un procedimento puramente formale e non è legato ad alcun caso particolare. Quindi in generale per qualunque problema esiste sempre una dimensione caratteristica che consente di metterlo in scala dal punto di vista geometrico.
di una parete piana. Tuttavia osserviamo che il procedimento che stiamo seguendo ora è un procedimento puramente formale e non è legato ad alcun caso particolare. Quindi in generale per qualunque problema esiste sempre una dimensione caratteristica che consente di metterlo in scala dal punto di vista geometrico.
Ricavando la variabile dimensionata ![]() in funzione della variabile adimensionale
in funzione della variabile adimensionale ![]() dall'espressione (7) risulta che :
dall'espressione (7) risulta che :
![]()
Ricavando la variabile dimensionata ![]() in funzione della variabile adimensionale
in funzione della variabile adimensionale ![]() dall'espressione (18) risulta che:
dall'espressione (18) risulta che:
![]()
Sostituendo dunque le espressioni (19) e (20) nella (17) risulta che:
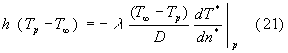
Ho adimensionalizzato la derivata portando fuori dal segno di derivata i fattori ![]() e
e ![]() , entrambi costanti. A questo punto posso dividere entrambi i membri per
, entrambi costanti. A questo punto posso dividere entrambi i membri per ![]() e ottengo:
e ottengo:
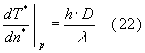
L'espressione (22) coincide con l'espressione (9) con cui avevamo introdotto il numero di Nusselt .Siamo arrivati a uno dei possibili significati fisici del numero di Nusselt per cui può essere visto come il valore adimensionalizzato del gradiente di temperatura alla parete. Facciamo notare che il gradiente è inteso nel verso positivo della normale alla parete, cioè allontanandoci da questa.
Un altro significato fisico lo si ottiene rielaborando in modo opportuno sempre l'espressione (22) e riscrivendola nella forma:
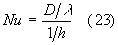
Allora notiamo che nella (23) il termine ![]() , presente a numeratore, rappresenta la resistenza termica di pura conduzione per unità di superficie di un materiale avente spessore
, presente a numeratore, rappresenta la resistenza termica di pura conduzione per unità di superficie di un materiale avente spessore ![]() e avente conducibilità
e avente conducibilità ![]() . Analogamente notiamo che il termine
. Analogamente notiamo che il termine ![]() , presente a denominatore, rappresenta la resistenza termica di convezione per unità di superficie al di fuori della parete. Allora il numero di Nusselt esprime quante volte la resistenza termica di pura conduzione di una parete con spessore
, presente a denominatore, rappresenta la resistenza termica di convezione per unità di superficie al di fuori della parete. Allora il numero di Nusselt esprime quante volte la resistenza termica di pura conduzione di una parete con spessore ![]() e avente conducibilità
e avente conducibilità ![]() è grande rispetto alla resistenza termica di convezione tra una parete e un fluido ai quali è assegnato il coefficiente di convezione
è grande rispetto alla resistenza termica di convezione tra una parete e un fluido ai quali è assegnato il coefficiente di convezione ![]() .
.
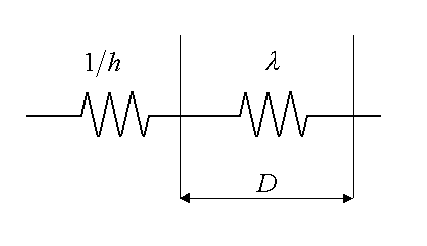
Figura 9 - interpretazione del numero di Nusselt con le resistenze termiche
Fisicamente si può interpretare il numero di Nusselt come un rapporto tra due resistenze termiche: una di pura conduzione e l'altra di convezione. Il numero di Nusselt risulta allora tanto più grande quanto la resistenza di pura conduzione è grande rispetto alla resistenza di convezione. Questo fatto spiega perché il numero di Nusselt è generalmente maggiore di uno. La convezione scambia maggiormente calore rispetto alla pura conduzione, il che significa che la resistenza termica di convezione è normalmente minore della resistenza termica per pura conduzione, e dunque il rapporto di tali resistenze risulta maggiore di uno.
Se il fluido all'esterno della parete restasse immobile, troveremmo un valore del numero di Nusselt circa uguale a 1, poiché confronteremmo tra loro due resistenze termiche che di fatto, con il fluido fermo, si equivalgono.
Esperienza in cui il numero di Nusselt è 1
Ci chiediamo allora se esiste un caso sperimentale, facilmente realizzabile, in cui il fluido è impossibilitato a muoversi di modo che si trovi ![]() . Questo caso esiste e lo rappresentiamo qui brevemente. Consideriamo il caso della cavità con la parete superiore e inferiore che permettono il passaggio di calore, e con le pareti laterali adiabatiche, ovvero isolate termicamente. Poniamo a contatto con la parete superiore un serbatoio caldo, e a contatto con la parete inferiore un serbatoio freddo.
. Questo caso esiste e lo rappresentiamo qui brevemente. Consideriamo il caso della cavità con la parete superiore e inferiore che permettono il passaggio di calore, e con le pareti laterali adiabatiche, ovvero isolate termicamente. Poniamo a contatto con la parete superiore un serbatoio caldo, e a contatto con la parete inferiore un serbatoio freddo.
La lunghezza caratteristica è in questo caso la distanza tra le due pareti non adiabatiche.
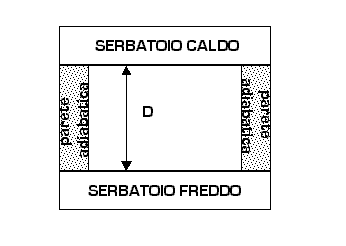
Figura 10 - cavità per ottenere in laboratorio un numero di Nusselt unitario
La parte del fluido posta superiormente dentro alla cavità si scalda e tende a restare verso l'alto poiché avrà una densità minore. La parte del fluido posta inferiormente dentro alla cavità si raffredda e tende a restare verso il basso dal momento che avrà una densità maggiore. Se non c'è alcun agente forzante esterno, come può essere una ventola azionata da un motore elettrico, il fluido tende a restare fermo così com'è e non si instaurano correnti convettive all'interno della cavità. Se il fluido è immobile il numero di Nusselt vale ![]() e posso sostituire questo valore nella (23) ricavando:
e posso sostituire questo valore nella (23) ricavando:
![]()
Misurando la distanza ![]() e conoscendo il valore della conducibilità
e conoscendo il valore della conducibilità![]() del fluido posso trovare il coefficiente di convezione
del fluido posso trovare il coefficiente di convezione ![]() in un modo facilmente realizzabile in laboratorio. In tutti gli altri casi, non appena il fluido incomincia a muoversi il numero di Nusselt supera l'unità. Durante il moto di un fluido che scorre in regime laminare si trovano valori abbastanza bassi del numero di Nusselt. Ad esempio se consideriamo il moto dell'acqua che scorre in regime di moto laminare entro un tubo troviamo dei valori del numero di Nusselt che sono di poco superiori a
in un modo facilmente realizzabile in laboratorio. In tutti gli altri casi, non appena il fluido incomincia a muoversi il numero di Nusselt supera l'unità. Durante il moto di un fluido che scorre in regime laminare si trovano valori abbastanza bassi del numero di Nusselt. Ad esempio se consideriamo il moto dell'acqua che scorre in regime di moto laminare entro un tubo troviamo dei valori del numero di Nusselt che sono di poco superiori a ![]() e in particolare si ottengono valori diversi a seconda che consideri le condizioni al contorno di temperatura imposta o flusso imposto. Non appena il moto passa da regime di moto laminare a moto turbolento il valore del numero di Nusselt cresce e può valere qualche decina o alcune centinaia come nel problema precedente in cui abbiamo trovato
e in particolare si ottengono valori diversi a seconda che consideri le condizioni al contorno di temperatura imposta o flusso imposto. Non appena il moto passa da regime di moto laminare a moto turbolento il valore del numero di Nusselt cresce e può valere qualche decina o alcune centinaia come nel problema precedente in cui abbiamo trovato ![]() . Nel caso del problema si verifica uno scambio termico di natura convettiva che è circa 400 volte più efficace dello scambio termico che avremmo avuto per pura conduzione lasciando scaldare il fluido fermo a contatto con il tubo. Comprendiamo allora come il valore numerico del numero di Reynolds mi dice quante volte lo scambio convettivo è amplificato rispetto allo scambio conduttivo che avrei per opera del fluido stagnante, che giace fermo nel tubo.
. Nel caso del problema si verifica uno scambio termico di natura convettiva che è circa 400 volte più efficace dello scambio termico che avremmo avuto per pura conduzione lasciando scaldare il fluido fermo a contatto con il tubo. Comprendiamo allora come il valore numerico del numero di Reynolds mi dice quante volte lo scambio convettivo è amplificato rispetto allo scambio conduttivo che avrei per opera del fluido stagnante, che giace fermo nel tubo.
Condizione al contorno fluidodinamica adimensionalizzata
Così come abbiamo ricavato il numero di Nusselt dall'adimensionalizzazione della condizione al contorno termica, allo stesso modo vogliamo ricavare un espressione in cui compaia il numero di Reynolds dall'adimensionalizzazione della condizione al contorno fluidodinamica .
Consideriamo un fluido che scorre lungo la direzione x e lambisce una parete. Se consideriamo la direzione y normale alla parete stessa, lungo tale direzione si avrà un profilo parabolico della velocità come si vede in figura 11.
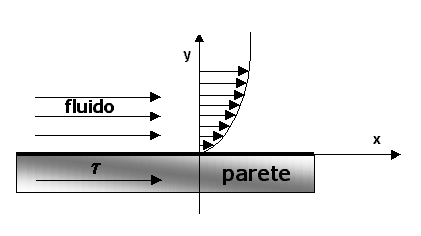
Figura 11 - profilo parabolico della velocità di un fluido che lambisce una parete
Abbiamo definito la velocità adimensionale ![]() con l'espressione (8)
con l'espressione (8)
![]()
dove:
![]()
![]() è la velocità del fluido lontano dalla parete.
è la velocità del fluido lontano dalla parete.
La velocità adimensionale, definita così, vale ![]() alla parete e vale
alla parete e vale ![]() a distanza infinita dalla parete che interagisce con il fluido in moto. Il fluido che scorre sulla parete sviluppa uno sforzo tangenziale
a distanza infinita dalla parete che interagisce con il fluido in moto. Il fluido che scorre sulla parete sviluppa uno sforzo tangenziale ![]() che tende a trascinare con sé la parete. Posso esprimere matematicamente l'entità dello sforzo tangenziale
che tende a trascinare con sé la parete. Posso esprimere matematicamente l'entità dello sforzo tangenziale ![]() tramite due espressioni. In primo luogo esprimiamo
tramite due espressioni. In primo luogo esprimiamo ![]() con la legge di Newton che abbiamo introdotto nella prima lezione di fluidodinamica:
con la legge di Newton che abbiamo introdotto nella prima lezione di fluidodinamica:
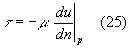
Posso esprimere lo sforzo tangenziale ![]() in funzione del coefficiente
in funzione del coefficiente ![]() . Avevamo trovato nelle lezioni precedenti l'espressione:
. Avevamo trovato nelle lezioni precedenti l'espressione:
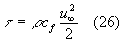
Unendo la (25) con la (26) abbiamo che:
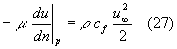
Seguendo lo stesso procedimento di prima, andiamo ad adimensionalizzare il gradiente di velocità alla parete![]() presente nella (27). Per fare questo oltre a creare una variabile adimensionale della velocità, come abbiamo fatto nella (8) in cui figura la velocità adimensionale
presente nella (27). Per fare questo oltre a creare una variabile adimensionale della velocità, come abbiamo fatto nella (8) in cui figura la velocità adimensionale ![]() , dobbiamo creare una variabile adimensionale anche per la normale, come abbiamo fatto nella (18) in cui compare la già nota normale adimensionale
, dobbiamo creare una variabile adimensionale anche per la normale, come abbiamo fatto nella (18) in cui compare la già nota normale adimensionale ![]() . Ricavando la variabile dimensionata
. Ricavando la variabile dimensionata ![]() in funzione della variabile adimensionale
in funzione della variabile adimensionale ![]() dall'espressione (8) risulta che:
dall'espressione (8) risulta che:
![]()
Dall'espressione (20) abbiamo :
![]()
Sostituendo queste due espressioni nella (27) abbiamo che:
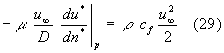
Possiamo ricavare dalla (29) il gradiente di velocità alla parete adimensionalizzato:
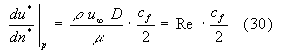
dove abbiamo riconosciuto nel fattore ![]() il numero di Reynolds. Il gradiente della velocità alla parete è proporzionale al numero di Reynolds e al coefficiente
il numero di Reynolds. Il gradiente della velocità alla parete è proporzionale al numero di Reynolds e al coefficiente ![]() .
.
Analogia di Reynolds
Abbiamo visto che sia per il problema termico che per il problema fluidodinamico è stato possibile definire due variabili di tipo adimensionale, ![]() e
e ![]() che variano nello stesso range di valori e cioè sono comprese tra 0 e 1. Inoltre entrambi i problemi sono governati da equazioni che in forma adimensionale sono abbastanza simili.
che variano nello stesso range di valori e cioè sono comprese tra 0 e 1. Inoltre entrambi i problemi sono governati da equazioni che in forma adimensionale sono abbastanza simili.
Per il problema termico vale l'equazione di Fourier che in forma adimensionale si esprime così :
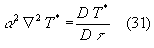
dove a secondo membro compare la derivata sostanziale rispetto al tempo.
Per il problema fluidodinamico vale l'equazione di Navier che in forma adimensionale si esprime così :
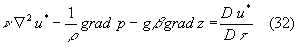
dove anche qui a secondo membro compare la derivata sostanziale rispetto al tempo.
Osservo che il secondo membro della (31) e il secondo membro della (32) sono già formalmente identici dal momento che entrambe sono derivate sostanziali rispetto al tempo e che![]() e
e ![]() variano nello stesso range di valori.
variano nello stesso range di valori.
Se voglio che queste due equazioni diventino formalmente simili devo poter trascurare i due termini con segno meno a primo membro della (32). In generale questi due termini non sono trascurabili e quindi, in generale non è vero che la soluzione del problema termico coincida con la soluzione fluidodinamica. In quei casi particolari in cui nel problema fluidodinamico posso trascurare il gradiente di pressione![]() e non si applica il termine
e non si applica il termine ![]() dovuto all'applicazione delle forze gravitazionali, se valgono le condizioni di similitudine tra il problema termico e quello fluidodinamico, per quanto abbiamo visto dalla teoria dei modelli, la soluzione delle due tipologie di problemi coincide.
dovuto all'applicazione delle forze gravitazionali, se valgono le condizioni di similitudine tra il problema termico e quello fluidodinamico, per quanto abbiamo visto dalla teoria dei modelli, la soluzione delle due tipologie di problemi coincide.
Consideriamo il problema fluidodinamico in cui una lastra piana orizzontale come può essere un laghetto viene investito dall'aria. In tal caso non ho gradiente di pressione in quanto l'aria che lambisce il laghetto ha la stessa pressione ovunque che coincide con la pressione atmosferica. Immaginiamo che l'aria soffi orizzontalmente sopra il laghetto di modo che non ci sia una componente del moto lungo l'asse z e dunque non si applica nemmeno il termine dovuto alle forze gravitazionali. In tal caso anche la parte relativa al laplaciano nel primo membro viene a coincidere. Quello che ostacola una perfetta analogia tra le due equazioni è la presenza dei due coefficienti ![]() e
e ![]() che sono in generale diversi. La condizione di similitudine mi chiede che
che sono in generale diversi. La condizione di similitudine mi chiede che ![]() affinché la soluzione del problema fluidodinamico sopra esposto coincida con la soluzione di un problema termico che vogliamo risolvere (e che in generale è più complicato). Ma abbiamo già visto dalla (6) che
affinché la soluzione del problema fluidodinamico sopra esposto coincida con la soluzione di un problema termico che vogliamo risolvere (e che in generale è più complicato). Ma abbiamo già visto dalla (6) che ![]() significa avere un numero di Prandtl
significa avere un numero di Prandtl ![]() .
.
Ipotizziamo ora che tutto il pacchetto di ipotesi esposte sopra siano vere e che valga anche la condizione di similitudine ![]() allora posso impostare il problema termico e il problema fluido dinamico con la stessa equazione. Appurato che le condizioni al contorno siano le stesse, allora anche il risultato dei due problemi sarà lo stesso e la temperatura
allora posso impostare il problema termico e il problema fluido dinamico con la stessa equazione. Appurato che le condizioni al contorno siano le stesse, allora anche il risultato dei due problemi sarà lo stesso e la temperatura ![]() coinciderà con la velocità
coinciderà con la velocità ![]() . Allora da
. Allora da ![]() si ricava che:
si ricava che:
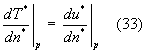
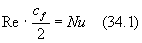
Questo modo di ragionare per analogia è chiamato analogia di Reynolds e si esprime dicendo che problemi fluidodinamici e problemi termici, costituiscono lo stesso problema se se valgono tutte le ipotesi semplificative che abbiamo fatto per cui possiamo considerare che i problemi abbiano le stesse condizioni al contorno.
Quindi se ho fatto degli esperimenti fluido dinamici che mi hanno portato a determinare il valore di ![]() e di
e di ![]() io posso utilizzare questi stessi risultati per calcolare il numero di Nusselt e viceversa!
io posso utilizzare questi stessi risultati per calcolare il numero di Nusselt e viceversa!
Normalmente l'analogia di Reynolds non viene scritta come in (34.1) , ma con l'espressione:
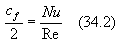
Analogia di Reynolds generalizzata
Ferme restando le ipotesi per cui possiamo trascurare le forze gravitazionali e il gradiente di pressione, cosa succede se abbiamo ![]() ? Vale ancora l'analogia di Reynolds? Così come è scritta nella (34.1) non è più vera. Si scopre tuttavia che l'analogia di Reynolds diventa vera in una forma generalizzata in cui oltre alle variabili precedenti compare anche il numero di Prandtl e che si esprime nella forma:
? Vale ancora l'analogia di Reynolds? Così come è scritta nella (34.1) non è più vera. Si scopre tuttavia che l'analogia di Reynolds diventa vera in una forma generalizzata in cui oltre alle variabili precedenti compare anche il numero di Prandtl e che si esprime nella forma:
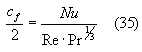
Non vogliamo illustrare come si ricava l'espressione dell'analogia di Reynolds generalizzata dal momento che è legata a una trattazione troppo complicata e tuttavia rimarchiamo che questa ha un'alta validità purché siano rispettate le condizioni per le quali è possibile trascurare i gradienti di pressione e le forze gravitazionali.
Trascurare i gradienti di pressione implica un restringimento della soluzione di problemi con una geometria molto semplificata. È invece possibile postulare l'assenza degli effetti gravitazionali ogni qualvolta ci troviamo in condizioni forzate, dal momento che se la velocità del fluido è abbastanza forte è possibile coprire totalmente gli effetti naturali con quelli dovuti alle azioni forzanti.
L'utilizzo dell'analogia di Reynolds mi permette di ricavare il numero di Nusselt dalla conoscenza di parametri come ![]() ,
, ![]() e
e ![]() che sono molto più facili da determinare sperimentalmente rispetto a quanto sia possibile fare con
che sono molto più facili da determinare sperimentalmente rispetto a quanto sia possibile fare con ![]() . Infatti per determinare
. Infatti per determinare ![]() dovrei utilizzare delle termocoppie , mentre per determinare
dovrei utilizzare delle termocoppie , mentre per determinare ![]() mi basta una semplice prova in galleria del vento.
mi basta una semplice prova in galleria del vento.
Notiamo anche il significato fisico insito nella (35). Crescere lo scambio termico significa crescere le perdite di carico. Non è possibile far crescere lo scambio termico e contemporaneamente ridurre le perdite di carico. I due fenomeni sono strettamente legati. Anche quando non sono verificate le ipotesi semplificative per cui nella (35) non vale più il segno di uguaglianza vale sempre un discorso di proporzionalità tra scambio termico e perdite di carico che è legato a un concetto fisico generale. Un esempio estremamente illuminante a tal riguardo è la gestione del raffreddamento di una vettura da "formula uno" o di una motocicletta da corsa. In questi casi da un lato vorrei avere un buono scambio termico per raffreddare il motore e dall'altro vorrei diminuire le perdite di carico per non frenare la vettura. Se doto il mezzo di batterie alettate con superficie sovradimensionate in modo da migliorare lo scambio termico devo mettere in bilancio una perdita nelle prestazioni di velocità. Alla base di questo criterio di progetto sta l'analogia di Reynolds.