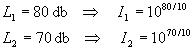
Titolo lezione: Propagazione esterna
Somma di due livelli sonori
Suppongo di avere 2 sorgenti incoerenti (L1 e L2),quindi devo sommare le due intensità.
Come si vede si è avuto un incremento inferiore ai 0,5 decibel, si può quindi affermare che se uno dei due livelli è inferiore all’altro di 10 decibel il suo contributo alla somma è praticamente trascurabile.
Questo appare evidente osservando il seguente diagramma:
Differenza di livelli
Supponiamo di voler calcolare il rumore prodotto da una macchina, per farlo bisogna considerare anche il rumore prodotto dall’esterno (L0) che si misura con la macchina spenta, quindi bisogna fare una differenza di livelli sonori.
Questo è il rumore prodotto dalla nostra macchina.
Livello di potenza
Si definisce livello di potenza (Lw):
Esso serve per misurare quanto una sorgente emette.Il livello di potenza non è un livello sonoro, ma energetico.
Esso assume valori diversi e scorellati dal livello di inntensità.
Figura 1:Fronti d’onda di una sorgente puntiforme
Figura 2: Sorgente puntiforme in campo libero
Solo in alcuni casi si può trovare una relazione tra i due livelli, come illustreremo adesso per la sferetta sonante (sorgente puntiforme in campo libero):
Figura 3: Dispersine del suono da una sorgente puntiforme
Prendiamo ad esempio:
Si possono quindi avere dei livelli altissimi di potenza.
E’ da notare anche che con sorgenti puntiformi ogni volta che raddoppio la distanza ho una diminuzione del livello di intensità di 6 decibel.
Questo si nota chiaramente dal seguente diagramma che rappresenta i livelli di intensità in funzione della distanza:
Consideriamo invece una sorgente sonora lineare come può essere ad esempio un autostrada:
Figura 4: Dispersione del suono da una sorgente lineare
Dove LW’ è il livello di potenza su metro quadrato.
Si vede subito come nel caso di una sorgente lineare il livello sonoro diminuisce ogni raddoppio della distanza.

Consideriamo infine il caso di una sorgente piana, come può essere il muro di un edificio:
Figura 6: Sorgente piana
Un caso significativo da prendere in considerazione è quello di un osservatore dotato di strumento di misura sonoro che si allontana perpendicolarmente da un muro di un edificio.
Figura 7 :Osservatore che si allontana dall’edificio
All’inizio vedrà l’edificio come una sorgente piana, superati i 5 m di distanza lo considererà come una sorgente lineare e infine ad una distanza superiore i 200 m l’edificio potrà essere considerato come una sorgente puntiforme.
Quindi i livelli di intensità sonora si comporteranno come nel seguente diagramma:
Attenuazioni in eccesso
In verità bisogna tenere conto delle attenuazioni provocate dalle situazioni reali come l’atmosfera che ci circonda aggiungendo quindi un fattore di correzione.
Nel caso della sorgente lineare l’equazione viene corretta così:
Ad esempio una causa di attenuazione può essere il vento
Se un suono passa da una zona in cui non è presente il vento in una in cui è presente, la velocità del suono si somma vettorialmente con quella del vento.
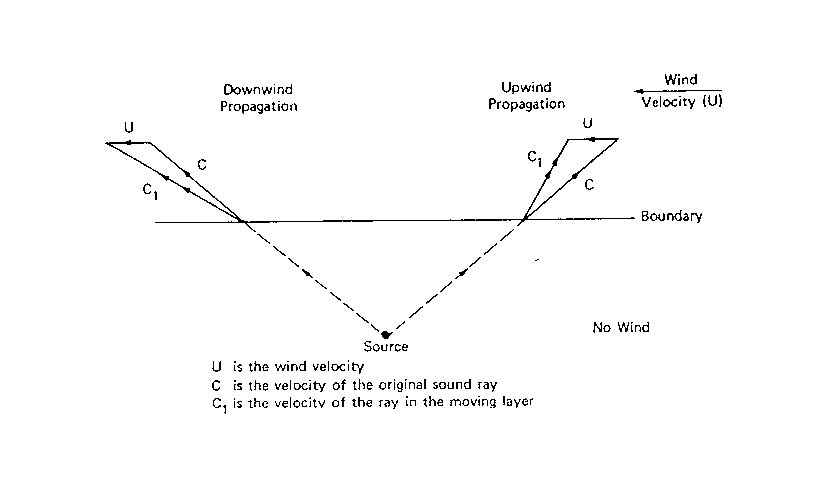
Ad esempio se noi abbiamo una sorgente rialzata da terra e il vento che varia linearmente con la quota si tenderanno a creare attorno alla sorgente a livello del terreno delle zone d’ombra in cui non si sentirà il suono proveniente dalla sorgente stessa.
Un altro fattore importante è la temperatura dell’aria, infatti di solito essa diminuisce con l’aumentare dell’altezza, ma si possono verificare delle zone di inversione termica in cui c’è un aumento di temperatura nonostante aumenti l’altezza dal suolo.
Si possono avere anche delle strane situazioni (c) in cui c’è una lama di aria che porta il suono lontano anche per chilometri.
Figura 9: Tipico gradiente della temperatura
La situazione (a) fa si che la temperatura decrescente porti i raggi che seguono il freddo ad inclinarsi verso l’alto e a far si che si creino delle zone di ombra.
Nella situazione (b) di inversione termica i raggi sonori si inclinano dalla parte opposta e può anche succedere che superano degli ostacoli tipo dei muri, in questo caso non si creano delle zone di ombra.
E’ molto difficile tenere conto delle attenuazioni dovute a questi fenomeni, infatti non esistono delle formule precise, ma ci sono le complicatissime regole ISO 9613.
Tecnica della sorgente immagine
Questa tecnica serve per calcolare i livelli d’intensità dei raggi sonori riflessi dal terreno. E’ lecito costruire la sorgente immagine solamente se il terreno su cui si riflette il raggio è una superficie liscia e dura e con asperità piccole rispetto alla lunghezza d’onda.
Figura 11: Tecnica della sorgente immagine
Come si sommano i due raggi?
Dipende dalla natura del suono, se il suono è uguale e periodico i due suoni interferiscono.
Se i due segnali sono in fase si crea un segnale con una potenza fino a 6 decibel più alta, in verità saranno meno di 6 decibel perché il segnale riflesso è sempre minore di quello diretto. In altri punti l’interferenza sarà distruttiva e quindi si potrebbero avere delle cancellazioni, in verità non si verificano delle cancellazioni ma delle diminuzioni di 10-15 decibel per la minore potenza del segnale riflesso.
Si potrebbe quindi fare il calcolo delle fasi per vedere quale sia il segnale risultante, ma questo calcolo sarebbe troppo instabile , infatti basterebbe cambiare solo leggermente la posizione del microfono per rifare tutti i calcoli.
Il discorso si fa più facile se ho un suono variabile in cui il segnale diretto e quello inverso sono completamente diversi, in questo caso si sommano le intensità.
In questo caso vale questa formula:
In questa formula non ho considerato l’assorbimento del terreno.
Assorbimento del terreno
Figura 12: Assorbimento del terreno
Si definisce coefficiente di assorbimento acustico (a ) e il coefficiente di assorbimento ( r):
Quindi considerando l’assorbimento la (6) diventa:
Assorbimento dell’aria
Si ha assorbimento massimo dell’aria quando l’aria secca, con l’aumentare di j
(grado idrometrico) diminuisce l’attenuazione dell’aria.
L’attenuazione dell’aria dipende anche dalla frequenza del suono ed è maggiore con l’aumentare della frequenza, infatti all’aperto l’attenuazione subita dai suoni con frequenze basse è praticamente trascurabile.
Esiste anche una formula che vale fino a quando la relazione tra attenuazione e frequenza è lineare.
Figura 13:Attenuazione dovuta all’assorbimento atmosferico in funzione dell’umidità e della frequenza
Diffrazione e schermatura
E' il fenomeno che si verifica quando un suono a basse frequenze passa attraverso un muro di cinta o attraverso un buco nel muro.
Figura 15: Effetto della diffrazione alle alte frequenze
Il buco e il muro diffraggono l'onda e si formano dei fronti d'onda che sembrano provenire dal bordo di diffrazione stesso.
E’ molto difficile studiare questo effetto, e ci si riesce solo in casi molto semplici; uno di questi è il caso degli schermi sottili di lunghezza infinita che è stato studiato e viene rappresentato nella formulazione di Maekawa
Esiste anche il diagramma di Maekawa dove viene rappresentate le variazioni di D L in funzione di N.
Teorema di Fourier
Un qualsiasi suono complesso p(t ) può essere descritto come una sommatoria di infinite sinusoidi e cosinusoidi ognuna dotata di una propria ampiezza, frequenza e fase.
Trasformata discreta di Fourier
Di solito non è possibile considerare un numero infinito di sinusoidi e quindi si fa un approssimazione discretizzando sia il numero di sinusoidi che quello di cosinusoidi, sia le frequenze e le ampiezze.
Questa operazione mi permette di passare dal segnale nel dominio del tempo in quella della frequenza e di determinarne quindi lo spettro.
Figura 16:Spettro del segnale
Nello spettro non compare nessuna informazione sulla fase del nostro segnale.
In verità non ha molto senso parlare di fase assoluta perché essa dipende dalla distanza dalla sorgente; ha invece senso parlare di fase relativa soprattutto quando si usano degli strumenti di misura con più canali.
Lo spettro risulta molto utile quando voglio calcolare il livello totale del suono, infatti posso fare la somma dei livelli delle righe spettrali.
In questo caso posso fare la somma energetica trattandosi di linee spettrali indipendenti ognuna delle quali dotate di una sua frequenza specifica.
Il livello sonoro calcolato con questo procedimento è uguale a quello calcolato conoscendo la forma d’onda.