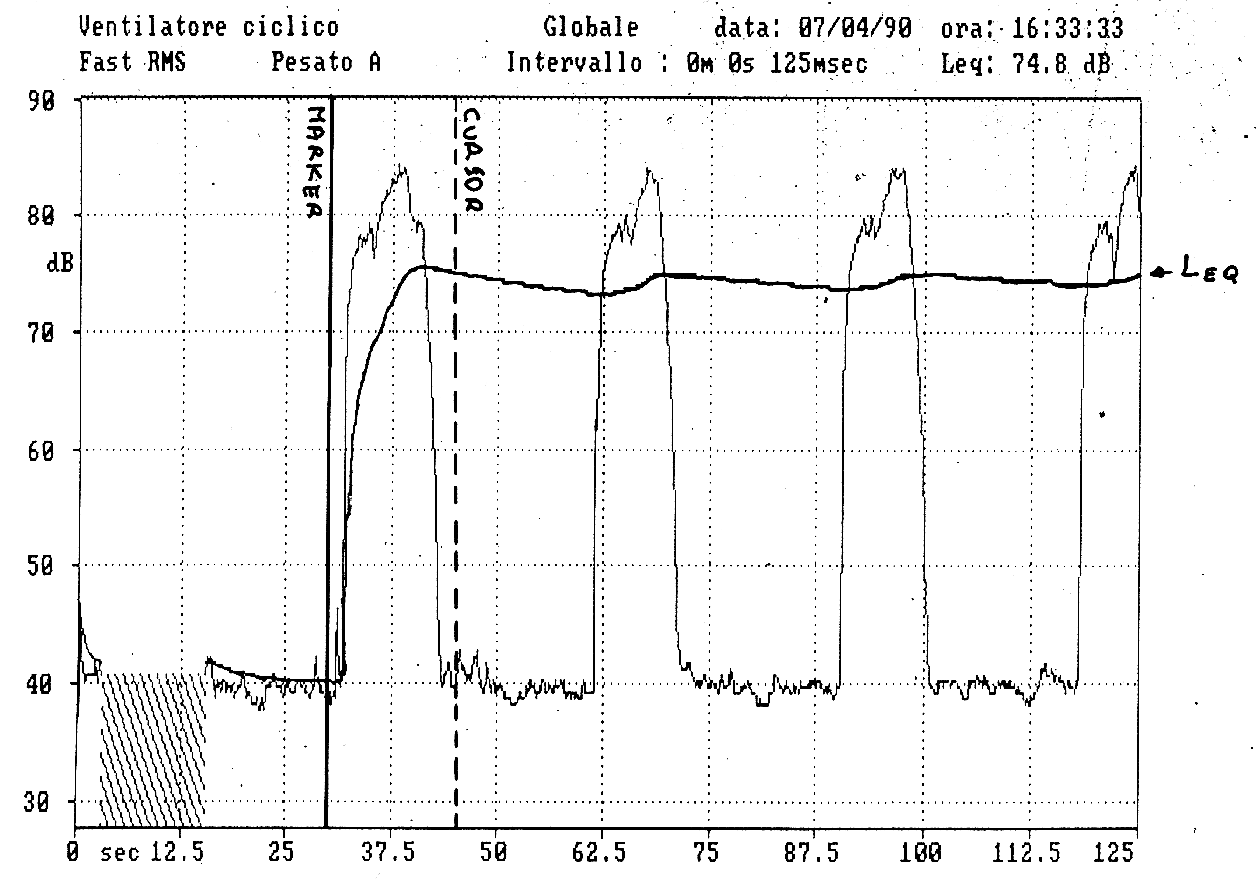
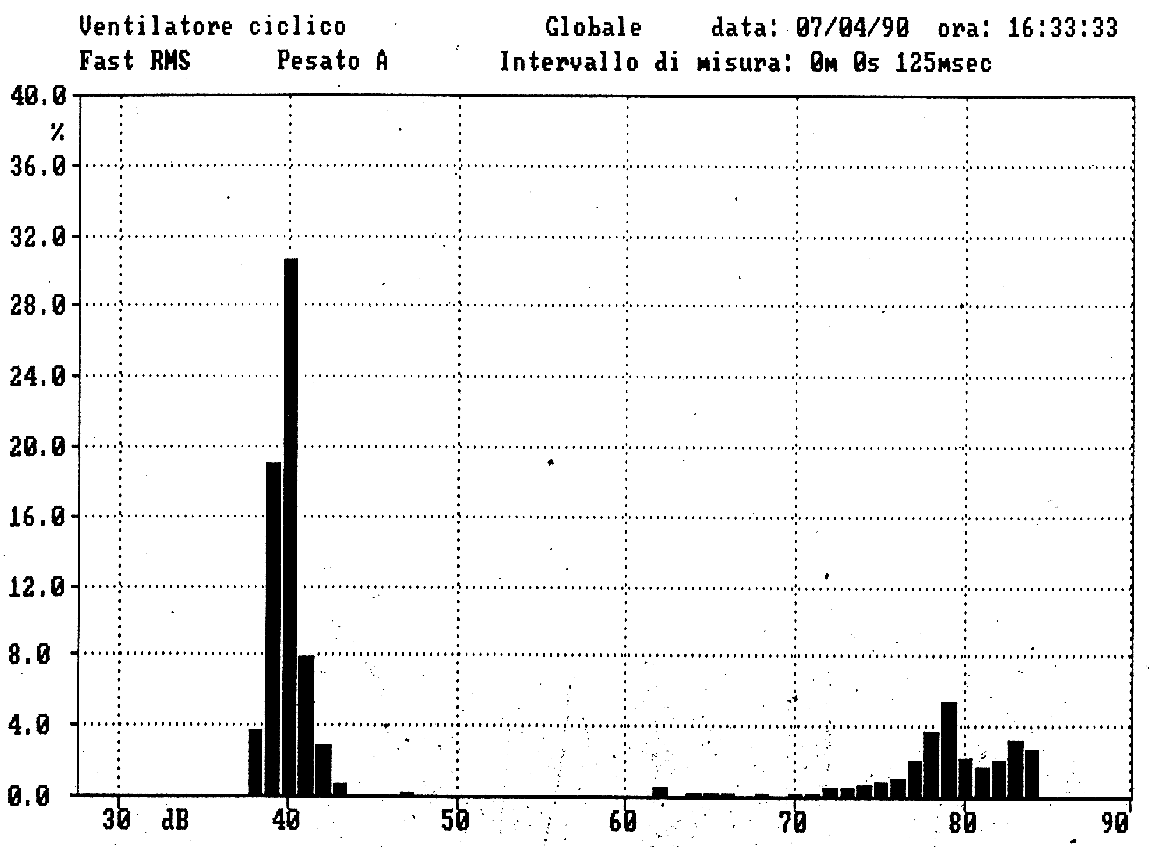
Nell’esempio in figura abbiamo un rumore pressoché costante nel quale si manifestano, ogni tanto, dei picchi dovuti all’azionamento di un ventilatore. In tutti questi casi è chiaramente possibile calcolare il L_eq, però il semplice valore del L_eq non la dice tutta su cosa è successo nel frattempo nel corso della misura. In questo caso sono successe molte cose: c’è un rumore di fondo molto basso e periodicamente ci sono punte di rumore. Se si lascia partire lo strumento e lo si lascia integrare nel tempo il L_eq assume l’andamento mostrato in figura. Se si guarda il valore del L_eq si leggono 74dB. Questo valore contiene indubbiamente delle informazioni importanti sul rumore che c’è stato, ma non dice del fatto che il rumore è variato. Lo stesso L_eq si sarebbe potuto ottenere per un rumore che non aveva queste forti variazioni ma che oscillava stabile intorno al valore medio. Non si riesce cioè a discriminare questi due fenomeni. Per fare ciò è necessario utilizzare l’analisi statistica che è fatta costruendo un istogramma che riporta le frazioni del tempo totale di misura in cui è stato presente ciascun livello sonoro. Nell’istogramma sono indicati in ascissa i livelli sonori ed in ordinata le percentuali del tempo complessivo di rumore in cui è stato presente quel livello sonoro.

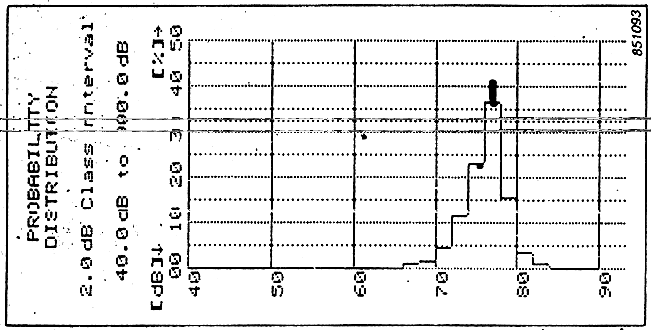
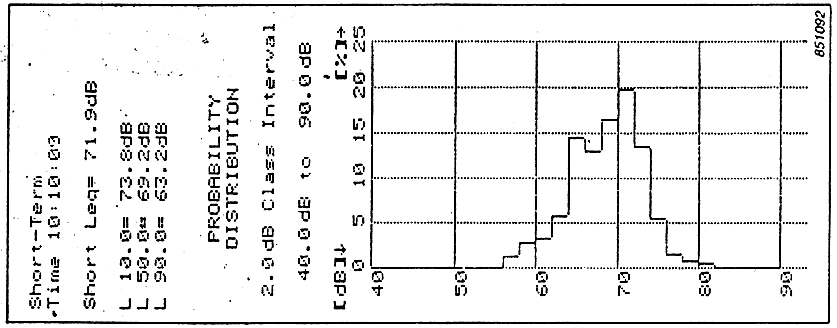
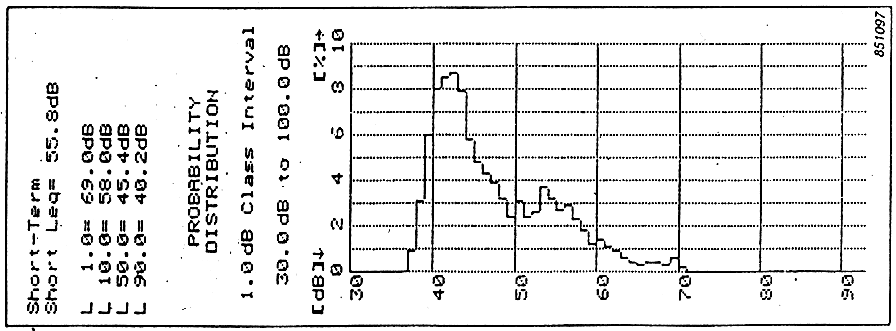
Qua si ha un segnale che sta variando nel tempo e l’istogramma corrispondente rappresenta i tre casi di rumore diverso.

Quando sotto una banda c’è scritto un valore, ad esempio 60 e questo valore è il 6%, vuol dire che per il 6% del tempo il livello è stato maggiore od uguale a 60 e minore di 61. Ogni banda può avere una qualunque larghezza, ma solitamente si usano bande larghe 0,5dB. La somma dei livelli di tutte le bande di tutti i livelli deve essere 100.

L’istogramma può essere tradotto in una curva chiamata curva statica distributiva. Questa curva può essere costruita automaticamente dallo strumento che digitalizza l’istogramma e rende possibile il trasferimento di tali dati sul computer tramite collegamento seriale.

La curva statistica distributiva corrispondente all’esempio del ventilatore sarà formata da due campane, una, del rumore di fondo, centrata sui 40dB e l’altra, riguardante la messa in funzione del ventilatore, centrata sugli 80dB. Da questa curva e dall’istogramma corrispondente, si possono ricalcolare i L_eq parziali di ogni singolo rumore che fa parte del rumore complessivo. In questo esempio il rumore del ventilatore ha una potenza così superiore al rumore di fondo che quest’ultimo diventa irrilevante al fine del calcolo del L_eq totale.

Ci sono casi non così fortemente sbilanciati ove il L_eq non è dominato da solo un livello di rumore, come ad empio in questo grafico ove il rumore di fondo è dato dal traffico stradale ed ogni tanto si avverte il rumore del treno che è molto più raro. Quindi si ha una grande campana dovuta al traffico ed una campana molto più piccola riferita al rumore del treno.

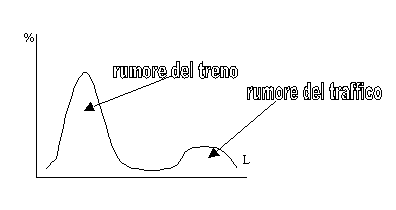
Se si va ad integrare magari si ottiene un L_eq del traffico pari a 65dB ed un L_eq del treno pari a 68dB. Ed è questo il modo corretto, utilizzando appunto un’analisi statistica con i percentili, di calcolare il L_eq di due rumori che coesistono nel periodo di misura e che non è facile separare in altro modo.

In molti casi si ha solo il L_eq complessivo e l’analisi statistica e non sempre si ha uno strumento in grado di memorizzare ogni intervallo di misurazione il valore del rumore. Il grande vantaggio dell’analisi statistica è che il numero di numeri che vanno memorizzati non cresce con il tempo di misura. Con l’analisi statistica una volta che si stabilisce un range di misura per lo strumento e la classe, ad esempio da 20dB a 100dB con classe 1dB, ci sono un numero predefinito di numeri da memorizzare qualunque sia la durata della misura. L’analisi statistica è una tecnica consente di buttare via moltissimi numeri pur mantenendo un’informazione sufficiente a separare fra loro le varie correnti sonore.

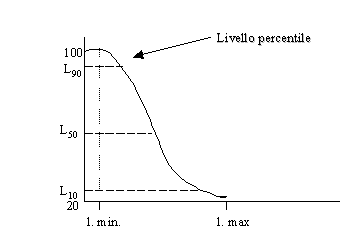
Dalla curva statistica distributiva si passa alla curva statistica cumulativa. La curva statistica cumulativa rappresenta sempre una percentuale del tempo, ma una percentuale del tempo in cui si è superato un certo livello. Quindi se si parte da un livello basso, ad esempio 20dB, abbiamo superato 20dB dal 100% di tempo; man mano che cresce il livello comincia ad esserci una frazione del tempo in cui il livello è stato più basso del valore che abbiamo in ascissa e quindi questa curva inizia a scendere fino a che raggiunge il valore nullo e si hanno il livello massimo e quello minimo.

Matematicamente si può calcolare l’integrale sommando tra loro i valori delle bande partendo da 100 e sottraendo via via i valori delle bande che si incontrano ed in questo modo si ricostruisce matematicamente la curva cumulativa a partire da quella distributiva.

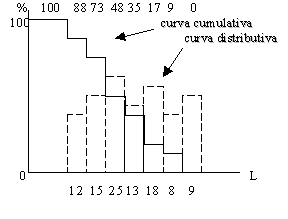
Di fatto l’informazione contenuta nella curva distributiva è la stessa contenuta in quella cumulativa.

Sulla curva cumulativa vengono definiti i livelli percentili che rappresentano i livelli superati per una certa percentuale del tempo. Ad esempio L₉₀ indica il livello che si è superato per il 90% del tempo. Per misurare i livelli percentili lo strumento ha bisogno dei livelli fast. L’analisi statistica ha senso solo in relazione ad una ben precisa costante di tempo e questa costante di tempo deve essere la costante fast che vale 0,125s che corrisponde approssimativamente al vettore risposta dell’udito umano. In questo modo l’analisi statistica da un’idea piuttosto esatta di quella che è la variabilità del rumore che è stata percepita soggettivamente dall’uomo.

Se prendiamo delle costanti di tempo più grandi della costante fast il valore misurato tenderà ad essere più vicino al valore medio e la curva distributiva tenderà a stringersi tutta attorno ad un valore molto vicino al L_eq.

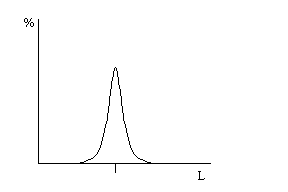
Se al limite il tempo di integrazione coincide con il tempo di misura totale si avrà un solo dato coincidente con il valore medio e la curva distributiva si ridurrà ad un’unica riga in corrispondenza di quel valore. Se viceversa usassimo delle costanti di tempo più piccole della costante fast la curva distributiva sarebbe molto più appiattita.

Lo strumento, quando fa una misura di L_eq, memorizza da tre a cinque percentili impostabili dall’utente, ma che normalmente, quando sono tre, sono L₁₀, L₅₀ e L₉₀ e quando sono cinque si aggiungono L₅ o L₁ e L₉₅ o L₉₉.

Per poter però ricostruire perfettamente la curva distributiva è necessario collegare lo strumento al PC, altrimenti gli unici dati che appaiono sul display dello strumento sono i livelli percentili e L_min e L_max con i quali si può in ogni modo costruire un abbozzo di curva cumulativa. Questi dati possono sembrare scarsi ed invece se ne possono ricavare molte informazioni. Ad esempio se si trova che la differenza fra L₁₀ e L₉₀ è di 1dB o 2dB significa che il rumore è stabile fra i due valori, cioè c’è stato un clima acustico stabile. Se viceversa L₁₀ vale 90 e L₉₀ vale 30, allora c’è stato un 10% del tempo con valori maggiori di 90 e solo un 10% del tempo con valori minori di 30 e ciò significa che il clima acustico è variabilissimo.

Il sistema uditivo umano è in grado di abituarsi al rumore. Se il rumore è stabile, anche se forte, non da poi tanto fastidio perché il nostro sistema uditivo compensa il rumore e ci può resistere. Quello che è estremamente disturbante e dannoso è la presenza di un rumore fortemente variabile che non da tempo al nostro sistema uditivo di adattarsi via via alle variazioni di rumore.

Per misurare l’intensità dei microfoni a pressione si prendono due microfoni a pressione posti ad una certa distanza d uno dall’altro. Quando un’onda, che supporremo piana e progressiva, passa lungo la congiungente di questi due microfoni, questi ultimi danno due segnali di pressione diversi p1 e p2.

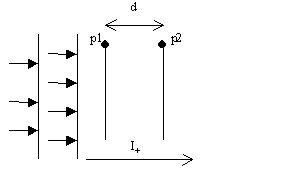
Fra p1, p2 e la velocità esiste il legame dato dall’equazione di Eulero.

Da questa equazione diventa così possibile calcolare la velocità delle particelle facendo:

Per uno strumento digitale fare l’integrale nel tempo è facile e quindi non è un problema. Mentre si hanno delle difficoltà a calcolare il gradiente della pressione. Per ovviare a questo si approssima il gradiente della pressione con il rapporto fra la differenza di pressione dei due microfoni e la distanza che li separa.

per

Questa approssimazione, però, vale solo per lunghezze d’onda molto maggiori della distanza d, in modo da commettere un errore trascurabile. All’aumentare della frequenza questa approssimazione non è più vera e l’errore che si commette inizia ad essere rilevante. Questo errore si chiama errore delle differenze finite.

Andando verso frequenze molto basse, il segnale si appiattisce talmente tanto che i due microfoni tendono a prendere lo stesso segnale. A questo punto la differenza tra i due segnali comincia ad essere così piccola da essere dello stesso ordine di grandezza della differenza tra i due microfoni. I microfoni non sono comunque uguali ed avranno in generale una diversa sensibilità ed una diversa risposta in fase, saranno cioè mal accoppiati in fase. Come accoppiamento in ampiezza è facile mettendo il caricatore dapprima su uno e poi sull’altro e regolando il guadagno dei due canali sullo strumento in modo da avere lo stesso segnale letto su entrambi. Molto più difficile è compensare un errore di fase. Se due segnali sono fra loro sfasati si legge una differenza che è maggiore di zero anche quando si sta dando lo stesso segnale ai due microfoni. Si montano allora i due microfoni faccia a faccia sul calibratore e si va a vedere cosa segna lo strumento. Se i due microfoni sono in fase lo strumento segna zero. Non è in ogni modo banale rimuovere il disaccoppiamento che è possibile rimuovere solo con strumentazione digitale piuttosto raffinata. Quindi l’unica soluzione è acquistare due microfoni già accoppiati in fase.

Questo diagramma mostra l’errore prodotto dallo sfasamento dei microfoni in funzione della reattività del campo ottenuto con microfoni che hanno un accoppiamento in fase migliore di 0,1 grado.

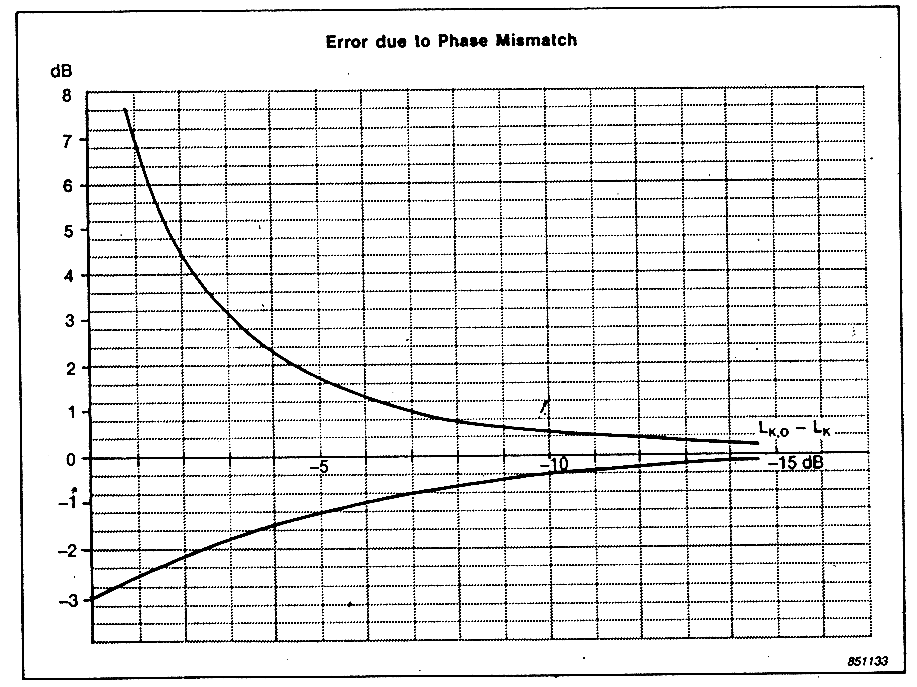
Tanto più si misura per un tempo breve tanto più cresce l’errore e questo dipende anche dall’indice di reattività. Il prodotto B x T è il prodotto della larghezza di banda in Hz per il tempo di misura in s quindi è adimensionale. Tanto più è grande il prodotto e tanto più ci si può permettere un indice di reattività elevato per commettere un certo errore percentuale.

Si prende una sonda intensimetrica commerciale e si monta fra le capsule microfoniche uno spaziatore che garantisce la distanza costante fra le due capsule. La scelta dello spaziatore influenza il campo di frequenza in quanto, se i microfoni sono molto vicini, funziona bene alle alte frequenze, se i microfoni sono lontani, funziona bene alle basse frequenze.

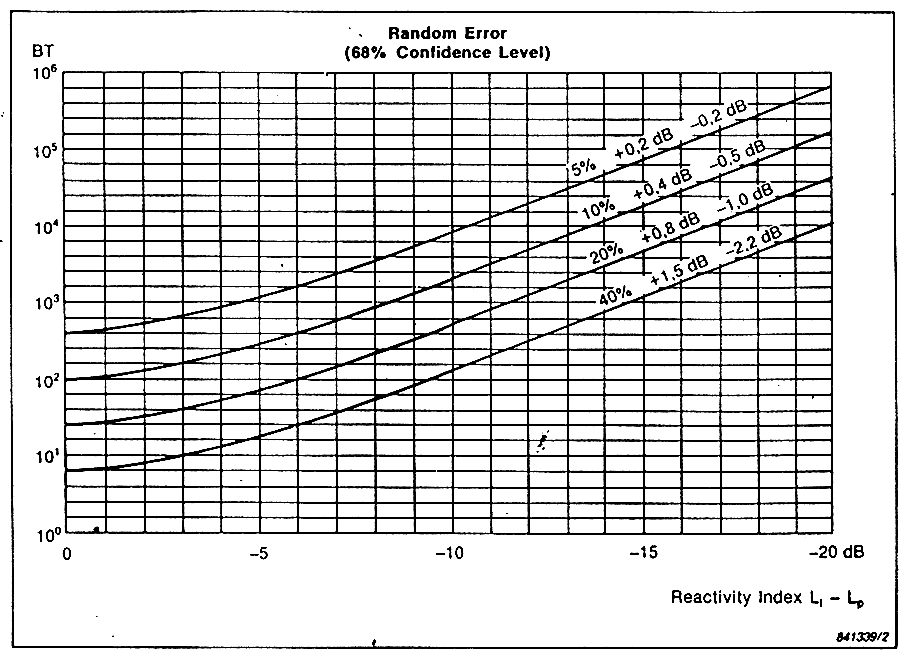
Qui abbiamo un diagramma che fa vedere il campo di misura utile con dei microfoni spaziati 6mm, 12mm, 50mm che sono le tre spaziature standard che si utilizzano in funzione del grado di accoppiamento in fase che hanno i microfoni. Se l’accoppiamento in fase è migliore di 0,3 gradi il campo di misura è la banda nera, se è migliore di 0,2 gradi il campo di misura è la banda tratteggiata e se l’accoppiamento in fase è migliore di 0,1 grado si riesce ad arrivare più in basso.

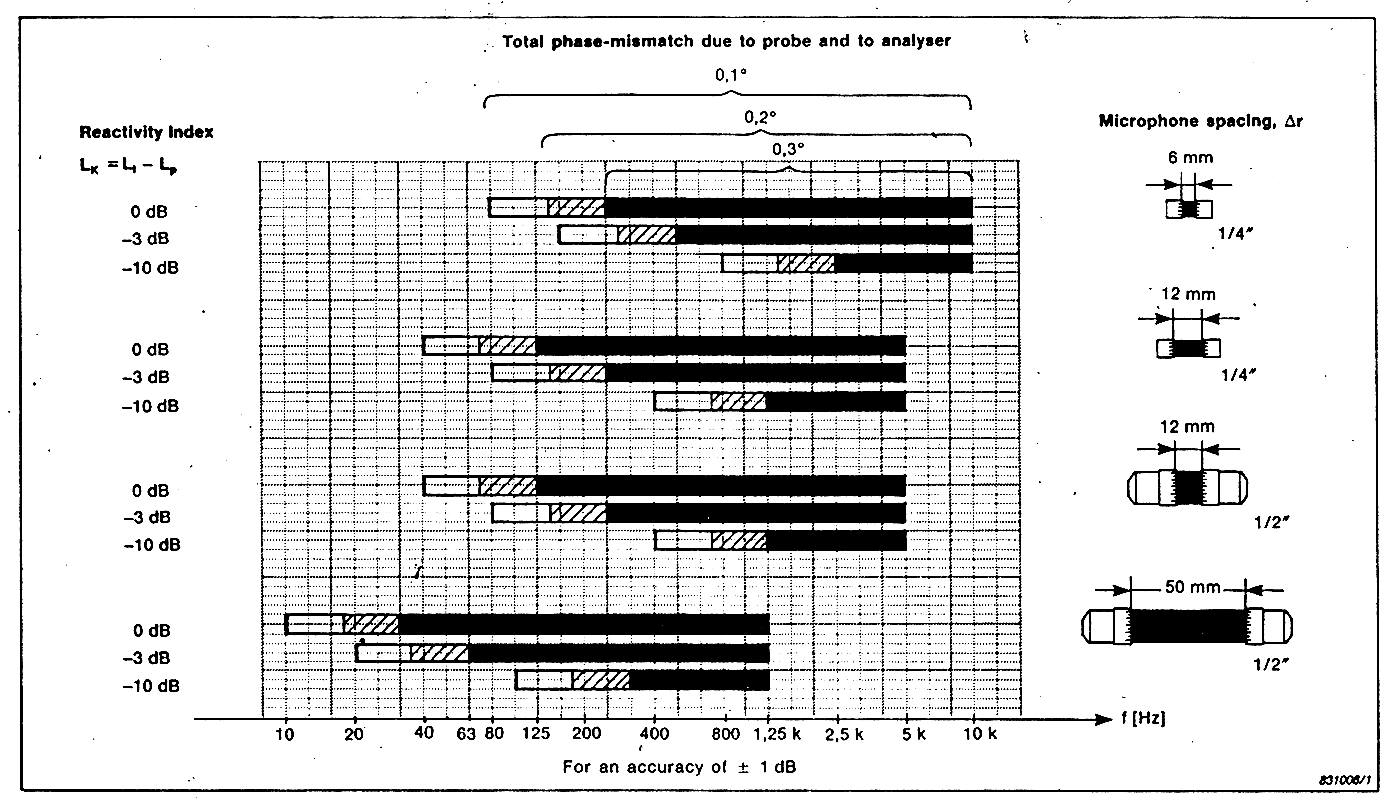
I valori scritti 0dB, 3dB, 10dB sono i cosiddetti indici di reattività del campo. L’indice di reattività del campo veniva definito fino a pochi anni fa come la differenza fra il livello di tensione ed il livello di intensità. La maniera di valutare l’indice di reattività L_k è variata ed è:

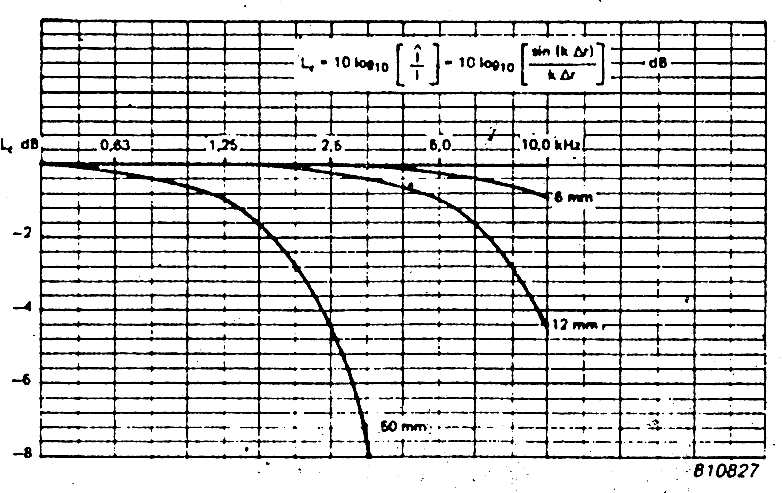
Tanto maggiore è l’energia stazionaria rispetto all’energia che si propaga, tanto più la misura è difficile, soprattutto a bassa frequenza. Trovare un indice di reattività di 10dB non è così infrequente. Al crescere della reattività del campo sonoro si riduce il campo di misura possibile.

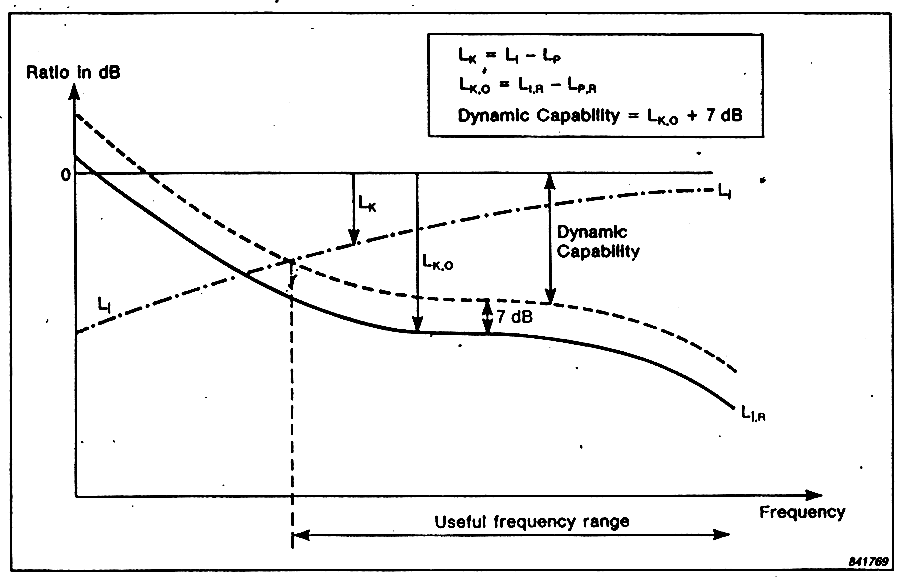
Il campo di misura utile dello strumento si ottiene prendendo il campo di reattività L_k0 ottenuto in condizioni di calibrazione e decrementando il campo dinamico di circa 7dB. La capacità dinamica di un intensimetro è 7dB in meno della differenza L_d - L_i che si misura in condizioni di calibrazione con in due microfoni accoppiati sul calibratore. L’intensimetro ha un campo dinamico di circa 20dB, quindi molto più ristretto rispetto a quello di un fonometro che è di circa 80dB. Ciò richiede di regolare accuratamente il fondo scala dello strumento in base all’intensità che devo misurare in modo che quest’ultima cada nel campo dinamico dello strumento.

L’intensità misurata ha un segno e può essere positiva se va dal microfono uno al microfono due e negativa se va nel verso opposto. L’intensimetro in realtà misura una componente cartesiana del vettore velocità, per la precisione quella lungo l’asse congiungente i due microfoni perché non calcola il vero gradiente, ma fa il rapporto fra le differenze di pressione e la distanza fra i due microfoni. Quindi gli spinotti BNC portano fuori due segnali di pressione ed uno di velocità, quindi è un microfono velocimetrico. Se prendiamo il segnale di velocità e andiamo a vedere quanto vale mettendo il microfono su un piatto rotante che gira e vado a fare la curva polare di risposta del microfono trovo un diagramma polare che rispetto all’asse x è:

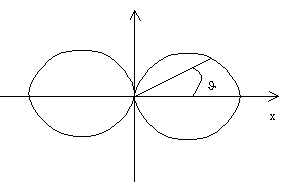
Ma se valuto questo in funzione dell’angolo J rispetto all’asse x l’ampiezza del segnale varia con il coseno dell’angolo J . Coseno che diventa anche negativo. Quando il segnale supera i 90° il segnale cambia segno e la polarità del segnale che esce dallo spinotto BNC finisce in controfase rispetto al segnale di pressione. Questo tipo di microfono si chiama microfono a velocità o microfono a figura di otto.

Questo microfono unito a quello a pressione consente di fare delle magnifiche registrazioni stereofoniche in quanto se si prendiamo i due segnali e andiamo a fare la somma e la differenza, e li buttiamo su due altoparlanti attraverso due canali U e P, ad esempio sull’altoparlante destro P+U e su quello sinistro P-U, succede che un suono che veniva da destra sarà con uguale ampiezza e uguale fase buttato su entrambi gli altoparlanti, i due segnali sono in fase e quindi avrò un segnale 2P, mentre sull’altoparlante di sinistra P-U vale zero ed il suono uscirà solo dall’altoparlante di destra. Se viceversa il suono fosse venuto da sinistra, il segnale del canale U andava in controfase e quindi avrò un segnale 2P sull’altoparlante sinistro e non uscirà suono da quello destro. I suoni che vengono da destra vanno quindi sull’altoparlante di destra, quelli che vengono da sinistra vanno all’altoparlante di sinistra e quelli che vengono da su o da giù non vengono presi dal segnale U ma solo dal segnale P. Quindi un suono che arriva da su o da giù viene riprodotto in modo uguale dai due altoparlanti. Questa è la base della tecnologia stereofonica. Chiaramente avere due altoparlanti posti a 180° rende impossibile riprodurre correttamente i suoni, perciò avendo a disposizione solo due canali si è preferito stringere l’angolo disponibile a circa 60° e gli impianti stereofonici tradizionali prevedono di utilizzare due altoparlanti posti ai vertici di un triangolo equilatero con l’ascoltatore posto al terzo vertice.

L’ideale sarebbe comunque avere un microfono che misura le tre componenti di velocità e che butta fuori i tre segnali delle velocità ed un segnale di pressione. Con quello ed utilizzando sei altoparlanti diventa possibile una ricostruzione tridimensionale completa del campo sonoro.

L’intensimetro dà la componente di un vettore, quindi o avendo una sonda tridimensionale o ripetendo la misura più volte, è possibile creare delle mappe vettoriali che misurano punto per punto la direzione in cui l’intensità sonora si sta propagando.

In questa immagine è stata mappata la rumorosità prodotta dal motore dell’autoveicolo dentro l’abitacolo di un’automobile ed ogni vettorino rappresenta direzione ed anche intensità.

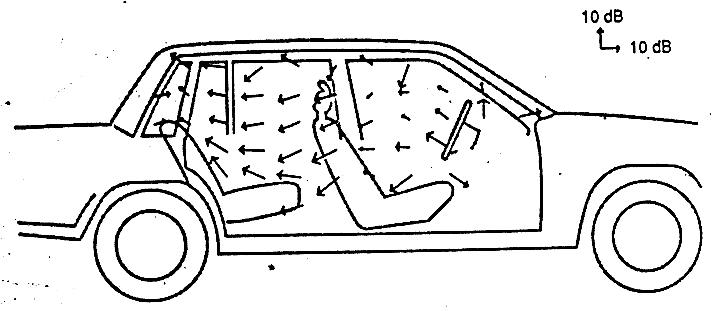
E’ anche possibile mappare il modulo dell’intensità come curva isolivello.

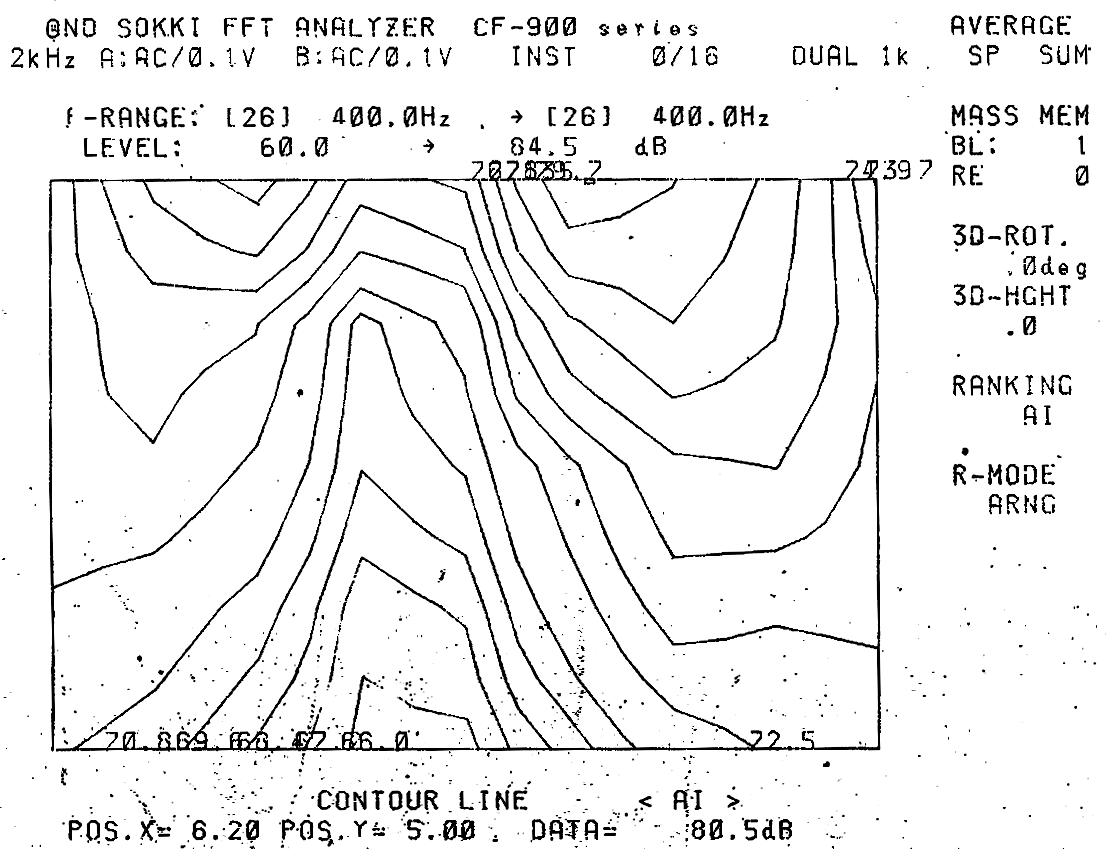
La tecnica intensimetrica viene solitamente accoppiata a sistemi di diagrammazione vettoriale dei valori misurati.

L’intensità è la misura ideale per trovare la potenza di una sorgente, quindi l’intensità misura la propagazione di un suono, cioè il fatto di non avere intensità significa solo che il suono non si sta propagando e non che non c’è. La sua principale utilità è quella di ottenere il livello di potenza e questo è possibile utilizzando il teorema di Gauss. Se abbiamo una sorgente ed andiamo a misurare la componente normale dell’intensità rispetto ad una certa superficie di area A ed in ogni punto misuriamo la componente normale del vettore intensità, vuol dire che dobbiamo sempre posizionare la sonda ortogonalmente alla superficie.

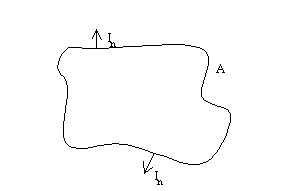
La tecnica intensimetrica è quindi una delle migliori tecniche per trovare la potenza di una sorgente. Le norme ISO che governano questa tecnica sono le norme ISO9614 parti 1 e 2.