Esercizio di dimensionamento di una pompa
Problema:
Si intende far fluire dell'olio per motori da una bacinella ad un'altra posta a 50 metri di altezza rispetto alla precedente. Per realizzare questo sistema si usa un tubo di diametro interno di 100 millimetri e di lunghezza 1 chilometro. La portata richiesta in volume è di 20 litri al secondo. Sono richieste la Potenza e la Prevalenza relative alla pompa.
Dati:
D h = 50 m ( altezza della seconda bacinella rispetto alla prima )
L = 1 km = 103 m ( lunghezza del tubo )
Dint = 100 mm = 10-1 m ( diametro interno del tubo )
![]()
DATI TABULATI:
m = 8,5 Poise = 0,85 Ns/m2 ( viscosità dinamica dell'olio per motori )
r = 0,92 g/cm3 ( densità dell'olio per motori )
Richiesti:
Potenza ( P ) e prevalenza della pompa ( D p ).
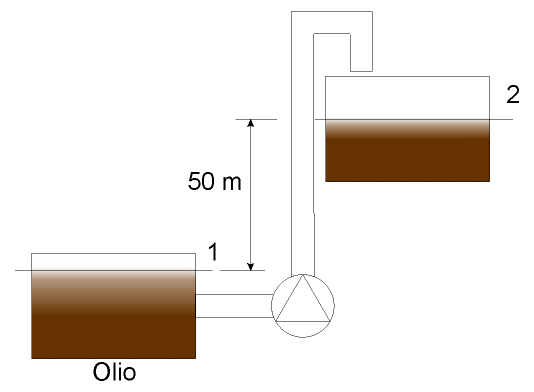
Figura 1 - Primo esercizio
Osservazioni:
Una pompa è caratterizzata da due dati principali: potenza e grafico prevalenza-portata. La prevalenza è per definizione la differenza di pressione uscita-ingresso della pompa e varia con la portata in volume secondo un grafico tipo quello a destra (curva A).
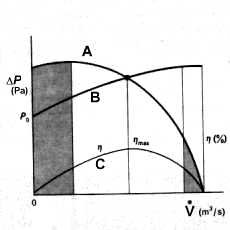
Grafico portata-prevalenza di una pompa (A), rendimento (C),
curva caratteristica di un sistema (B)
Sovrapponiamo a questo grafico quello che esprime le variazioni di pressione ingresso-uscita del circuito in relazione alla portata in volume (Curva B).
Il punto in cui le due curve si incontrano sarà il punto di lavoro del nostro sistema e cioé la coppia differenza di pressione-portata in volume raggiunta a regime dal sistema stesso. Una forte analogia si ritrova con la caratteristica volt-amperometrica di un generatore non ideale messa a confronto con quella di un carico resistivo. In un caso generale:
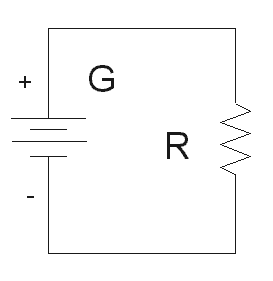
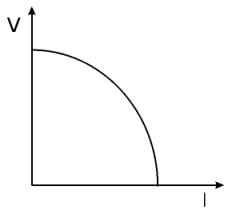
Curva caratteristica e schema di un circuito a carico resistivo
Questo è un esempio di come, grazie alla teoria dell'analogia, sia possibile ricavare da modelli di tipo elettrotecnico risultati validi anche in ambiti e discipline completamente differenti.
Notiamo inoltre che sarebbe buona norma sovradimensionare la portata in volume rispetto a quella prevista durante l'utilizzo potendo poi eventualmente ridurla usando una valvola regolabile.
Soluzione:
Una scelta opportuna delle sezioni permette di semplificare la soluzione delle equazioni. L'equazione di Bernoulli applicata al sistema ( trascurando gli a ) :
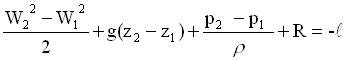
si semplifica scegliendo come sezioni i due peli liberi assunti dall'olio nelle bacinelle. Infatti:
L’equazione si semplifica in:
(1) ![]()
dove H rappresenta il dislivello e ![]() il lavoro compiuto dalla pompa. Applicando l’equazione di Bernoulli al sistema costituito dalla sola pompa si trova facilmente che in generale
il lavoro compiuto dalla pompa. Applicando l’equazione di Bernoulli al sistema costituito dalla sola pompa si trova facilmente che in generale 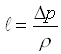 dove
dove ![]() è la densità del fluido.
è la densità del fluido.
R rappresenta le perdite di carico concentrate e distribuite, per cui può essere calcolato con la formula:
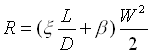
Possiamo calcolare W:
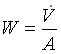 dove A è l’area della sezione normale del tubo e vale
dove A è l’area della sezione normale del tubo e vale 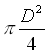 con D=100mm. Ne consegue che W = 2.55 m/s.
con D=100mm. Ne consegue che W = 2.55 m/s.
Ora, per calcolare le perdite di carico devo valutare in quale regime si muove l’olio: laminare o turbolento. Poichè l’olio è un fluido molto viscoso mi aspetto che sia laminare ma verifichiamo con i calcoli:
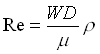 dove tutti i termini sono noti per cui: Re = 276 (<2300) e siamo in pieno regime laminare. In questo caso la relazione per il tubo tondo fra x
e Re è:
dove tutti i termini sono noti per cui: Re = 276 (<2300) e siamo in pieno regime laminare. In questo caso la relazione per il tubo tondo fra x
e Re è: 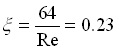 . Le perdite di carico distribuite sono:
. Le perdite di carico distribuite sono: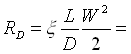 7539
7539 ![]() . L’unità di misura è
. L’unità di misura è ![]() perchè le perdite di carico sono energie specifiche per unità di massa di fluido. Le perdite di carico concentrate sono trascurabili essendo b
circa 3 per i tre gomiti e l’imbocco.
perchè le perdite di carico sono energie specifiche per unità di massa di fluido. Le perdite di carico concentrate sono trascurabili essendo b
circa 3 per i tre gomiti e l’imbocco.
Passiamo al calcolo della prevalenza della pompa:
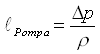 e dall’equazione 1:
e dall’equazione 1: 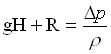
![]() 7387.6 Kpa = 73.87 bar
7387.6 Kpa = 73.87 bar
La potenza vale 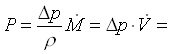 147752 W
147752 W
Una volta stabilito il punto di lavoro del nostro sistema (coppia ![]() ), bisogna dimensionare opportunamente la pompa. Se ne sceglierà una il cui grafico caratteristico passi per il punto trovato (o sia appena superiore) e il cui rendimento sia massimo in un suo intorno.
), bisogna dimensionare opportunamente la pompa. Se ne sceglierà una il cui grafico caratteristico passi per il punto trovato (o sia appena superiore) e il cui rendimento sia massimo in un suo intorno.

Grafico caratteristico di una pompa: il rendimento h max deve essere in
prossimità del punto di lavoro
Trovato il valore del rendimento h
sarà: 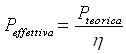 nel nostro caso @
250 KW. Il motore che aziona la pompa deve allora erogare almeno una potenza di 250 KW.
nel nostro caso @
250 KW. Il motore che aziona la pompa deve allora erogare almeno una potenza di 250 KW.
Esercizio sull’autoclave
Problema:
Dato il sistema in figura, determinare la prevalenza della pompa che garantisce una portata in massa di ![]() .
.
Dati:
D = 0.05 m
L = 8 m
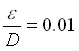
DATI TABULATI:
n = 10-6 m2/s ( viscosità cinematica dell'acqua )
r = 1000 Kg/m3 ( densità dell'acqua )
Diagramma di Moody
Nomogramma per le perdite concentrate
Richiesti:
Prevalenza della pompa ( D p ).

Figura 2 - Secondo esercizio
Soluzione:
Scegliamo i peli liberi come sezione di lavoro. L’equazione di Bernoulli si riduce a:
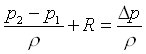 . Infatti i peli liberi hanno grande sezione, quindi le loro velocità sono trascurabili così come le variazioni di altezza.
. Infatti i peli liberi hanno grande sezione, quindi le loro velocità sono trascurabili così come le variazioni di altezza.
Le perdite di carico sono 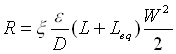 . Per trovare x
occorre il numero di Reynolds
. Per trovare x
occorre il numero di Reynolds 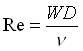 dove
dove 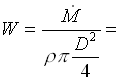 1.53 m/s. Re vale allora 76500 per cui siamo in regime turbolento. Dal diagramma di Moody:
1.53 m/s. Re vale allora 76500 per cui siamo in regime turbolento. Dal diagramma di Moody:
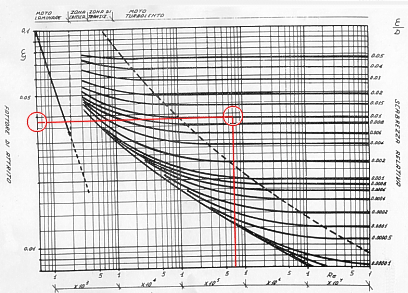
Diagramma di Moody: le linee in colore indicano come trovare il valore del fattore di attrito in base al numero di Reynolds e alla scabrezza relativa
si ricava un fattore di attrito x pari a 0.0385.
Dal Nomogramma si può ora colcolare la lunghezza equivalente dovuta all’imbocco ed allo sbocco.
Leq = 1.1 m (imbocco) + 1.7 m (sbocco) = 2.8 m.
Allora 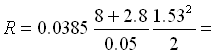 9.73
9.73 ![]()
La prevalenza che deve avere la pompa vale:
![]() 159700 Pa @
1.6 bar.
159700 Pa @
1.6 bar.
Nota: le perdite di carico dovute alla pompa sono considerate nel suo rendimento.
Esercizio: acqua in caduta
Problema:
Dato il sistema in figura, determinare da quale delle due vasche l’acqua cade più velocemente.
Dati:
D = 0.1 m per entrambi i tubi
L1 = 10 m
L2 = 20 m
e = 0 ovvero tubi lisci
DATI TABULATI:
n = 10-6 m2/s ( viscosità cinematica dell'acqua )
Diagramma di Moody
Richiesti:
Velocità di caduta dell’acqua.
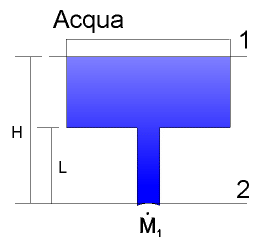
Figura 3 - Terzo esercizio
Soluzione:
Come prima approssimazione consideriamo H = L.
Scegliamo i peli liberi come sezione di lavoro. L’equazione di Bernoulli si riduce a:
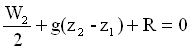 dove
dove 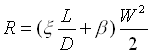 con b
= 1 a causa dell’imbocco. Infatti l’acqua al pelo è praticamente ferma rispetto alla velocità che assume in 2. Oltretutto i punti 1 e 2 si trovano entrambi a pressione atmosferica. Ne consegue:
con b
= 1 a causa dell’imbocco. Infatti l’acqua al pelo è praticamente ferma rispetto alla velocità che assume in 2. Oltretutto i punti 1 e 2 si trovano entrambi a pressione atmosferica. Ne consegue:
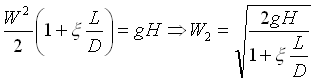 che è l’espressione generale della velocità. Possiamo notare subito che raddoppiare H non vuol dire raddoppiare le perdite di carico totali perchè il b
associato all’imbocco non varia. Ne consegue che la velocità aumenta se il tubo è più lungo.
che è l’espressione generale della velocità. Possiamo notare subito che raddoppiare H non vuol dire raddoppiare le perdite di carico totali perchè il b
associato all’imbocco non varia. Ne consegue che la velocità aumenta se il tubo è più lungo.
Il problema ora è calcolare x
che dipende da Re, il quale a sua volta dipende da W. Si procede ad una soluzione ricorsiva. Considero il tubo di lunghezza 10 m e parto da un valore di prova della velocità che può essere per esempio ![]() 14 m/s ovvero il massimo possibile, come se l’acqua cadesse come corpo libero senza attriti. Allora
14 m/s ovvero il massimo possibile, come se l’acqua cadesse come corpo libero senza attriti. Allora 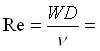 1.400.000 moto turbolento. e
è dato a 0 quindi nel diagramma di Moody si usa la curva più in basso relativa ai tubi lisci. Si ottiene: x
= 0.011 e quindi W* = 9.67 m/s. Ripetiamo usando questo valore di W per calcolare Re:
1.400.000 moto turbolento. e
è dato a 0 quindi nel diagramma di Moody si usa la curva più in basso relativa ai tubi lisci. Si ottiene: x
= 0.011 e quindi W* = 9.67 m/s. Ripetiamo usando questo valore di W per calcolare Re:
Re = 966584 turbolento
x = 0.012
W**=9.44 m/s
Re = 944361 turbolento
x = 0.012 indistinguibile dal valore precedente sul diagramma di Moody quindi scegliamo W**=9.44 m/s.
Questo meccanismo di calcolo ricorsivo funziona sempre perchè le curve di Moody sono monotone decrescenti. Di solito la ricorsione si ferma quando la variazione nei valori ottenuti riguarda cifre decimali oltre la terza.
Analogamente per il tubo da 20 m si ottiene:
W*=19.8 m/s
Re = 198090 turbolento
x = 0.0159
W**=9.68 m/s
Re = 968894 turbolento
x = 0.012
W***=10.74 m/s
Re = 1074298 turbolento
x = 0.0119
W****=10.77 m/s che consideriamo il valore risolutivo. Come previsto la velocità è più elevata.
Esercizio: la fontana
Problema:
Una fontana viene azionata da una pompa con prevalenza 1 bar. Si chiede l’altezza h raggiunta dallo zampillo.
Dati:
H = 2 m ( altezza dell’ugello )
D p = 1 bar
D = 0.04 m
d = 0.01 m
e = 0.05 mm
DATI TABULATI:
n = 10-6 m2/s ( viscosità cinematica dell'acqua )
r = 1000 Kg/m3 ( densità dell'acqua )
Richiesti:
Altezza h dello zampillo.
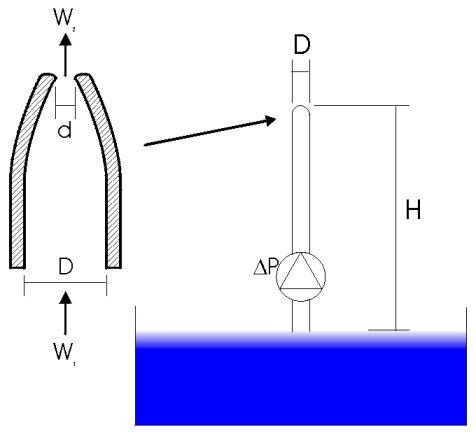
Figura 4 - Quarto esercizio
Soluzione:
Consideriamo le superfici determinate dal pelo dell’aqua nella fontana e dal ugello di uscita. l’equazione di Bernoulli :
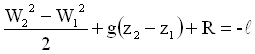 . Entrambe le velocità sono incognite quindi mi servirà un sistema di due equazioni e la prima è proprio quella di Bernoulli. La seconda si ottiene facilmente eguagliando le portate prima e dopo l’ugello per cui si ha W2 = 4W1.
. Entrambe le velocità sono incognite quindi mi servirà un sistema di due equazioni e la prima è proprio quella di Bernoulli. La seconda si ottiene facilmente eguagliando le portate prima e dopo l’ugello per cui si ha W2 = 4W1.
Cominciamo con il calcolare 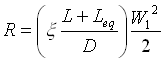 . La Leq della strozzatura dell’ugello vale 0.7 m e quindi
. La Leq della strozzatura dell’ugello vale 0.7 m e quindi 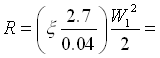 33.75×
x
×
W12.
33.75×
x
×
W12.
Il lavoro della pompa vale ![]() 100 J/Kg
100 J/Kg
L’equazione di Bernoulli diventa allora:
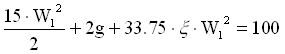 e quindi
e quindi 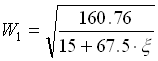 .
.
Per calcolare x mi serve però il numero do Re che dipende a sua volta da W1. Il problema si risolve attraverso il metodo ricorsivo.
Prendiamo come velocità di prova quella che l’acqua avrebbe se fosse x = 0.
W1 = 3.27 m/s.
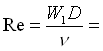 130800 turbolento
130800 turbolento
x = 0.016 dal diagramma di Moody
W*=3.16 m/s
Re = 126475 turbolento
x = 0.0159
W**=3.16 m/s che consideriamo il valore risolutivo. Allora W2 = 12.64 m/s.
L’altezza h vale: 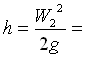 8.14 m.
8.14 m.
Esercizio: il serbatoio
Problema:
Calcolare la velocità di uscita dell'acqua dal serbatoio in figura e la sua portata in massa.
Dati:
H = 5 m
D = 0.15 m diametro del tubo di scarico
Angolo del tubo = 45°
e = 0.5 mm tubo di calcestruzzo
DATI TABULATI:
b = 5.5 della valvola e dell'imbocco
n = 10-6 m2/s ( viscosità cinematica dell'acqua )
r = 1000 Kg/m3 ( densità dell'acqua )
Richiesti:
Velocità di uscita dell'acqua e portata in massa.
Figura 5 - Quinto esercizio
Soluzione:
La lunghezza del tubo è L = 7.071. Consideriamo nulle la velocità del pelo libero e la variazione di pressione ambientale fra il pelo e lo sbocco. Anche il lavoro compiuto sul sistema è nullo e perciò l'equazione di Bernoulli si riduce a:
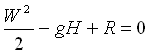 .
.
R = Rc+Rd =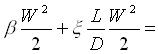 W2 ( 2.75 + 23.57x
). Mettendo questo nella formula si ottiene:
W2 ( 2.75 + 23.57x
). Mettendo questo nella formula si ottiene:
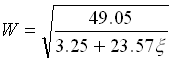 . Per calcolare x
valutiamo
. Per calcolare x
valutiamo 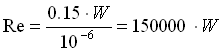 . A partire da un valore iniziale di
. A partire da un valore iniziale di ![]() 9.9 m/s procediamo per ricorsione:
9.9 m/s procediamo per ricorsione:
Re = 1485000 turbolento
scabrezza relativa = 0.0034
x = 0.028
W*=3.54 m/s
Re = 531281 turbolento
x = 0.028
W**=3.54 m/s che consideriamo il valore risolutivo.
La portata in massa è ![]() 6.34 Kg/s
6.34 Kg/s
Esercizio: la sorbona
Problema:
Determinare la portata in massa d'acqua della sorbona.
Dati:
L = 10 m
D = 0.5 m ( diametro del tubo )
e = 0.05 mm
![]()
DATI TABULATI:
n = 10-6 m2/s ( viscosità cinematica dell'acqua )
r acqua = 1000 Kg/m3 ( densità dell'acqua )
r aria = 1.03 Kg/m3 ( densità dell'aria a 20 °C )
Richiesti:
Portata in massa d’acqua.
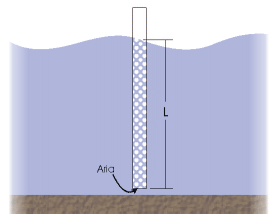
Figura 6 - Sesto esercizio
Soluzione:
Prima di tutto è importante capire secondo quale principio fisico funziona la sorbona: l’aria immessa dalla base sotto forma di piccole bollicine e l’acqua all’interno del tubo vengono considerate un unico fluido di densità inferiore a quello della sola acqua. Spinto dalla differenza di pressione il fluido misto sale verso la superficie.
Questo tipo di pompa viene utilizzato per esempio in mare per aspirare acqua quando la presenza di agenti in sospensione o di sabbia potrebbe interferire con il funzionamento di pompe meccaniche convenzionali.
Il problema principale nel formalizzare il meccanismo prima descritto è che salendo l’aria si espande per cui la densità del fluido diminuisce. Per i nostri calcoli impostiamo perciò due metodi risolutivi: nel primo, non considerando questa variazione di desità, troveremo una soluzione che a rigore sarà valida solo un un tratto infinitesimo all’inizio della sorbona. Successivamente useremo il risultato trovato come punto di partenza per un calcolo che comprenda la variazione di densità.
Un’approssimazione comune ai due metodi sarà di non tenere conto del differenziale di velocità fra acqua e aria: si ammetterà quindi che il fluido si comporti come se fosse omogeneo. Inoltre i calcoli funzionano bene finchè non intervengono termini di perdite di carico dovuti a turbolenze per la presenza di troppa aria rispetto all’acqua nel tubo. Il fluido misto è quindi quasi completamente acqua.
Primo metodo:
Impostiamo l’equazione di Bernoulli tenendo conto che, se non consideriamo l’espansione dell’aria, il fluido si mouve con la stessa velocità per tutta la sorbona. Inoltre la differenza di pressione fra le imboccature è data dalla legge di Stevino:
D P = r acqua× g× h
L’equazione di Bernoulli viene:
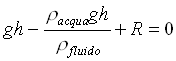 dove
dove 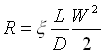 .
.
Prima di tutto 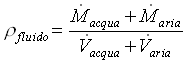 dove
dove ![]() 0.001 m3/s,
0.001 m3/s, 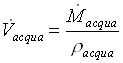 e per la stessa equazione è nota
e per la stessa equazione è nota ![]() . Per cui r
fluido rimane funzione solo di
. Per cui r
fluido rimane funzione solo di ![]() , a sua volta funzione della velocità di salita:
, a sua volta funzione della velocità di salita: ![]()
Come al solito per calcolare x
abbiamo bisogno del numero di Reynolds 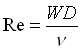 . Per poter procedere al calcolo per ricorsione impostiamo primi calcoli e mettiamo insieme le equazioni di cui disponiamo (e
/D = 0.0001):
. Per poter procedere al calcolo per ricorsione impostiamo primi calcoli e mettiamo insieme le equazioni di cui disponiamo (e
/D = 0.0001):
![]()
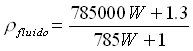
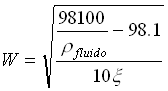
![]()
Re = 50000W
Scegliamo una prima velocità di tentativo di 0.7 m/s (ragionevole). Iterando si ottiene un risultato di W = 0.82 m/s e una densità del fluido r fluido= 998.47 Kg/m3 ovvero come se il fluido fosse quasi tutta acqua, come previsto. Questo comporta una portata in massa di fluido pari a r fluidoWS = 642,715 Kg/s che sono certo una grande quantità, anche se bisogna considerare che il tubo ha diametro di 50 cm. Questa è anche con buona approssimazione la portata in massa d’acqua perchè l’aria contribuisce solo per 0.0013 Kg/s sui più di 600.
Secondo metodo:
Consideriamo ora la variazione di desità del fluido. Impostare completamente il problema comporterebbe risolvere equazioni differenziali non facili quindi ci limiteremo a valutare un densità media e una velocità media di salita. Anche la velocità di salita del fluido infatti varia perchè l’aria espandendosi sale più velocemente. L’equazione di Bernoulli diventa:
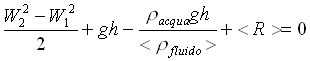 . I termini fra parentesi angolari sono valori medi sulla variazione lungo tutta la sorbona. Cerchiamo di rendere tutto funzione della W2, in modo da poter poi procedere con il metodo ricorsivo.
. I termini fra parentesi angolari sono valori medi sulla variazione lungo tutta la sorbona. Cerchiamo di rendere tutto funzione della W2, in modo da poter poi procedere con il metodo ricorsivo.
Prendiamo come valore di W1 quello calcolato prima: 0.82 m/s e lo stesso vale per r fluido, iniziale = 998.47 Kg/m3. Si ha comunque:
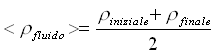
Per calcolare r
fluido, finale consideriamo che vale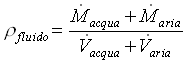 dove
dove ![]() questa volta cambia, per esempio linearmente al variare della pressione (isotermicamente):
questa volta cambia, per esempio linearmente al variare della pressione (isotermicamente): 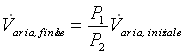 . Se la sorbona è alta 10 m il rapporto fra le pressioni vale 2 dato che la pressione atmosferica è di circa 1 atm e ogni 10 m la pressione dell’acqua aumenta di 1 atm. A 10 m di profondità vi sono quindi 2 atm di pressione. Il valore di
. Se la sorbona è alta 10 m il rapporto fra le pressioni vale 2 dato che la pressione atmosferica è di circa 1 atm e ogni 10 m la pressione dell’acqua aumenta di 1 atm. A 10 m di profondità vi sono quindi 2 atm di pressione. Il valore di ![]() è fissado dai dati e non varia. Diversamente
è fissado dai dati e non varia. Diversamente ![]() e
e 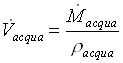 dipendono dalla velocità di salita dell’acqua:
dipendono dalla velocità di salita dell’acqua: ![]() . Per calcolare i valori finali saranno tutte funzioni di W2.
. Per calcolare i valori finali saranno tutte funzioni di W2.
Anche < R > va calcolata in base alla < W >, anche se ricordando che 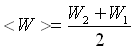 , si riesce a renderla funzione solo di W2 ( W1 = 0.82 m/s ). Stesso ragionamento anche per il numero di Reynolds:
, si riesce a renderla funzione solo di W2 ( W1 = 0.82 m/s ). Stesso ragionamento anche per il numero di Reynolds: 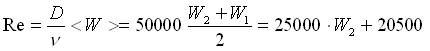 . Le equazioni che abbiamo a disposizione sono ora tutte funzioni di W2:
. Le equazioni che abbiamo a disposizione sono ora tutte funzioni di W2:
e /D = 0.0001
![]()
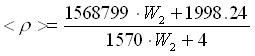
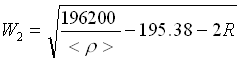
![]()
Scegliamo come W2 di prova proprio il valore di W1 = 0.82 m/s. Iterando si ottiene il valore ragionevole di W2 = 0.945 m/s per una < r > = 997.88 kg/m3. La < W > cercata è allora 0.8825 m/s da cui la portata in massa di fluido (che è circa quella dell’acqua) di 691,29 kg/s. Come ci si aspettava viene leggermente superiore.