Argomento della lezione :

Esercizio sui vapori surriscaldati
Esercizio sull’uso del calorimetro

ESERCIZIO N°1 : LO SCATOLONE ADIABATICO

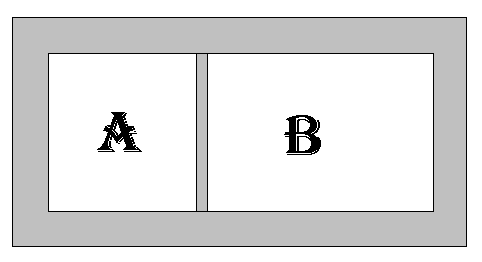
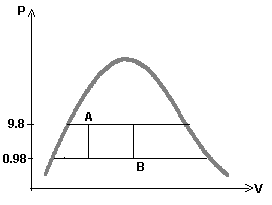
Il recipiente contiene vapor d’acqua surriscaldato A e B . I due vapori sono separati tra di loro da un isolante . Sappiamo che M_A=1 Kg , M_B=2 Kg , P_A=9.8 BAR , P_B=0.98 BAR , X_A=0.1 , X_B=0.5 .

In un secondo momento viene tolto il setto che divide due vapori, si chiede di studiare lo stato finale di questo sistema chiuso (cioè titolo, pressione e anche variazione di entropia)

RISOLUZIONE DEL PROBLEMA

Questo è un problema a volume costante, in cui non c’è scambio di calore . Per ciò l’energia interna del sistema finale si conserva.

U_C = U_A + U_C (1)

Inoltre osserviamo che il fenomeno non è lineare , non si può trattare con le leggi dei gas perfetti.

Osservando il classico grafico PV si vede subito che la soluzione sarà dentro il rettangolo delimitato da A e B. Non essendo il fenomeno lineare non troverò la soluzione sulla retta che unisce i due punti.

Osserviamo ora che in generale vale che :

U = M *( u_L + X_A* u_D) ( 2 )

Allora la ( 1 ) si può riscrivere come :

U_C = M_A * ( u_LA + X_A* u_DA) + M_B * (u_LB + X_B * u_DB ) ( 3 )

Ricaviamo ora u_A e u_B dalla opportuna tabella in funzione della pressione :

° C	P (BAR)	v_DM³/Kg	h_LKJ/Kg	r KJ/Kg	s_L KJ/(Kg*K)	v_L M³/Kg
70	0.3116	5.046	292.97	2334.0	0.9548	0.001022
80	0.4736	3.409	334.92	2308.8	1.0753	0.001029
90	0.7011	2.361	376.94	2283.2	1.1925	0.001036
100	1.0133	1.673	419.06	2256.9	1.3069	0.001043
150	4.760	0.3924	632.15	2113.2	1.8416	0.001090
155	5.433	0.3464	653.78	2097.4	1.8923	0.001096
160	6.181	0.3068	675.47	2081.3	1.9425	0.001102
165	7.008	0.2724	697.25	2064.8	1.9923	0.001108
170	7.920	0.2426	719.12	2047.9	2.0416	0.001114
180	10.027	0.1938	763.12	2013.1	2.1393	0.001127
190	12.551	0.1563	807.52	1976.7	2.2356	0.001415

Siccome noi conosciamo la pressione possiamo ricavare da questa tutti i dati termodinamici e sfruttare la (3) per ricavare U_C ( ricorda che h_L = u_L e u_D = r - P * v_D )

u_A = 763.12 + 0.1 * (2013 - 981* 0.1938 ) = 941 KJ/Kg

u_B = 419.06 +0.5 * (2256.9 - 98.1 * 1.673 ) = 1460 KJ/Kg

u_C= ( M_A * u_A + M_B * u_B) / M_C = ( 2* 1460 + 941) / 3 = 1287 KJ/kg

Sfruttando la tabella possiamo ricavare anche il volume occupato dalla nota relazione :

v = v_L + x* v_D (4 )

Dalla (4) si ha v_A = 0.0208 m³/ Kg e v_B = 0.863 m³/ Kg

Moltiplicando per la massa è ora facile ricavare il volume totale iniziale che sarà ovviamente uguale al volume finale :

V_A = v_A * M_A = 0.0208 m³/ Kg

V_B = v_B * M_B = 1.726 m³/ Kg

V_C = V_A + V_B = 1.7468 m³/ Kg

v_C = V_C / M_C = 0.582 m³/ Kg

Abbiamo così ricavato il volume specifico e l’energia interna dello stato finale ; dobbiamo ora cercare pressione e titolo. Restano sempre valide per lo stato C la (4) e la (2), perciò :

0.5823 = v_LC + X_F * v_DC
1287 = u_LF + X_F ( r_F - P_F * v_DF)

Queste sono due equazioni la cui unica vera incognita è X_F. Le altre grandezze si troveranno su una riga della tabella dell’acqua. In questi casi comunque non è possibile attuare una soluzione algebrica, useremo allora un metodo ingegneristico che consiste nel procedere per tentativi fino a che il sistema non è soddisfatto. Indicativamente sappiamo che la pressione sarà compresa tra 9.8 BAR e 0.98 BAR

Il risultato finale è P = 1.20 BAR e X = 0.40

Calcoliamo la variazione di entropia :

D S = M_C*s_C - ( M_A * s_A + M_B * s_C ) (5)

s_A =s_L + r_A/ T_A= 2.1393 + 0.1 * 4.443 = 2.58

s_B = s_L + r_B/ T_B= 1.312 + 0.5 * 6.022 = 4.323

s_c = s_L + r_C/ T_C= 1.352 + 0.4 * 5.996 = 3.750

Dalla (5) si ha che D S = 3 * 3.750 - 2.58 -2 * 4.323 = 0.03 kJ / K

ESERCIZIO N°2 :

In un tubo gira acqua alla pressione di 1 BAR e alla temperatura di 100°C. Si vuole conoscere la percentuale di vapore e liquido presenti nel tubo ( oppure il titolo X ) e per questo si fa gorgogliare da un piccolo ugello l’acqua in un calorimetro dove inizialmente la temperatura è di 25°C. La massa d’acqua nel calorimetro prima che l’acqua gorgogli è M₁ = 0.570 Kg ; la massa d’acqua finale è M_F = 0.615 Kg

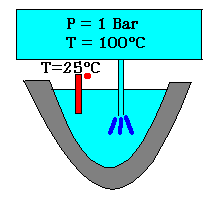
Osserviamo innanzitutto che il processo avviene a pressione costante di 1 BAR perché il calorimetro è a cielo aperto. Allora si conserva l’entalpia del sistema essendo : dh = dq + v * dp = dq (1)

Allora H₃ = H₁ + H₂ (2)

H₃ è lo stato finale del sistema dove resta solo acqua liquida ad una temperatura compresa tra 100°C e 25°C. H₁ è l’entalpia dell’acqua liquida presente all’inizio del processo e H₂ è l’entalpia del vapore umido all’inizio del processo (alla fine non ci sarà vapore). Ricordiamo poi che l’entalpia nel campo del liquido sottoraffreddato non varia

H₃ = M_F * C_P * T_F = (0.615) * 4.1886 * 64 = 164.86 KJ ( 3 )

H₂ = M₁ * C_P * 25 = ( 0.570 ) * 4.1186 * 25 = 59.68 KJ ( 4 )

H₁ = ( M_F - M₁ ) * ( h_L + X₁ * r1 ) = 0.045 * ( 419 + X * 2257 ) = 18.855 + 101.5 * X ( 5 )

E’ da notare che H₃ e H₂ sono stati trattati come liquidi e H₁ come vapore saturo.

Da quest’ultime equazioni si può ricavare facilmente il titolo X= 0.85

In generale comunque i calorimetri non vengono utilizzati nelle industrie per il costo elevato e perché funzionano unicamente a pressione atmosferica.