Fabio Giavarini matr. 112533
Lezione del 7/12/98 ore 8:30-10:30
Transitori Termici
INDICE
1. Introduzione: metodi di analisi 3
2. L’equazione della conduzione (o di Fourier) 3
3. Il metodo numerico 5
3.1 Discretizzazione del dominio 5
3.2 Discretizzazione del tempo 6
3.3 L’equazione di Fourier alle differenze finite 6
3.4 Passo temporale limite e ottimale
73.5 Esempio di calcolo
94. Programmi all’elaboratore 14
5. La formulazione implicita 19
1. INTRODUZIONE : I METODI DI ANALISI
In questa relazione si parlerà riguardo a problemi di conduzione del calore e ai loro metodi risolutivi. Tali problemi, nella pratica, causa un contorno irregolare e la non uniformità della temperatura, necessitano solitamente di una trattazione di tipo bi- o tridimensionale.
Ciò nonostante, in questa sezione, si preferirà dare grande rilievo a problemi monodimensionali, tali cioè che, sia la potenza termica, sia la temperatura, possano essere trattate come funzioni di una sola variabile.
Una simile scelta non dà luogo ad alcuna perdita di generalità. Questi problemi infatti, pur essendo meno complicati a risolversi, illustrano egualmente bene i fondamenti dei metodi di analisi utilizzati, che possono facilmente essere ampliati ai casi più complessi.
In una trattazione generalizzata, si dovrebbero evidenziare quattro principali metodi di analisi:
ma in questa sede si preferiranno i metodi numerici per le ragioni seguenti.
I metodi analitici richiedono una buona conoscenza delle serie di Fourier, delle funzioni di Bessel, dei polinomi di Legendre, delle trasformate di Laplace e della teoria delle variabili complesse, con una conseguente trattazione troppo avanzata per i nostri scopi. Tra gli altri tre metodi, spiccano per la loro immediatezza e semplicità proprio quelli numerici. Si preferirà pertanto una completa discussione dei suddetti, che, inoltre, si prestano particolarmente bene alla soluzione mediante calcolatori digitali.
A tal proposito si è dedicata un’ampia sezione allo studio di semplici programmi capaci di calcolare numericamente la conduzione del calore in una lastra discretizzata. Poiché essi usano un linguaggio di programmazione obsoleto come il qbasic non sarà tanto importante studiarne il listato, comunque inserito per ragioni di completezza, ma sarà necessario capirne il funzionamento, in quanto essi sono un potente strumento capace di risolvere agevolmente quei problemi la cui trattazione andiamo ora a incominciare.
2. L’EQUAZIONE DELLA CONDUZIONE (O DI FOURIER)
È necessario, ai fini della completa comprensione del problema, un breve richiamo sulla derivazione dell’equazione di Fourier, trattante la conduzione del calore.

Figura 2-1
: volumetto elementare nello spazioSupponiamo di avere un corpo solido e consideriamone un volumetto infinitesimo di spigoli dx, dy e dz, paralleli rispettivamente agli assi x, y e z di un diagramma cartesiano, come mostrato in figura 2-1. Scrivendo il bilancio di energia per tale elemento di volume si ottiene:
|
potenza termica entrante |
+ |
potenza termica generata da sorgenti interne |
= |
potenza termica uscente |
+ |
variazione energia interna nell’unità di tempo |
che, naturalmente, può essere posto in forma simbolica:
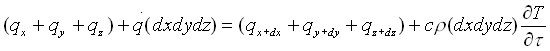 (1)
(1)
dove:
![]() è la potenza termica generata per unità di volume,
è la potenza termica generata per unità di volume,
T è la temperatura,
t è il tempo,
c è il calore specifico,
r è la densità.
Poiché in generale, Fourier aveva definito la potenza termica (dalla Legge di Fourier) come:
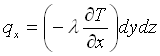 (2)
(2)
se viene considerata entrante lungo la direzione x come in figura 2-1, tenendo conto che l’elemento uscente dal volumetto, sempre nella medesima direzione, può essere scritto:
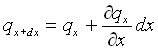 (3)
(3)
si ottiene che, generalmente:
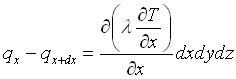 (4)
(4)
Poiché tale discorso può essere riportato lungo le altre direzioni con le medesime conseguenze, sostituendo tutto nell’equazione di bilancio e dividendo per dxdydz si ottiene:
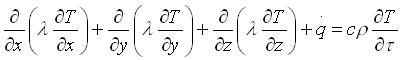 (5)
(5)
se il calore specifico c e la densità r sono indipendenti dal tempo.
Supponendo la conducibilità termica del materiale l uniforme e utilizzando la notazione di operatore vettoriale laplaciano, l’equazione può essere scritta nella forma più compatta:
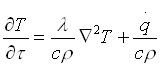 (6)
(6)
tale è una delle forme dell’equazione di Fourier. Il termine cr
viene chiamato inerzia termica mentre il termine ![]() definito dall’equazione:
definito dall’equazione:
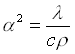
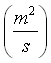 (7)
(7)
viene chiamato diffusività termica.
Ipotizzando infine che nel sistema non vi siano sorgenti di calore, si può finalmente scrivere:
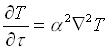 (8)
(8)
forma finale dell’equazione di Fourier, dalla quale partiremo per la trattazione del problema di transitorio termico.
3. IL METODO NUMERICO
Nei problemi pratici le condizioni al contorno e la geometria del sistema non consentono di utilizzare né la soluzione analitica né quella analogica. In questi casi si può, tuttavia, risolvere il transitorio per via numerica. Ci si basa sullo scrivere l’equazione di Fourier alle differenze finite, particolarmente adatte allo studio tramite calcolatori digitali. Nel nostro esempio, essa verrà scritta per una lastra piana e indefinita, in modo che il problema risulti unidimensionale.
3.1 DISCRETIZZAZIONE DEL DOMINIO
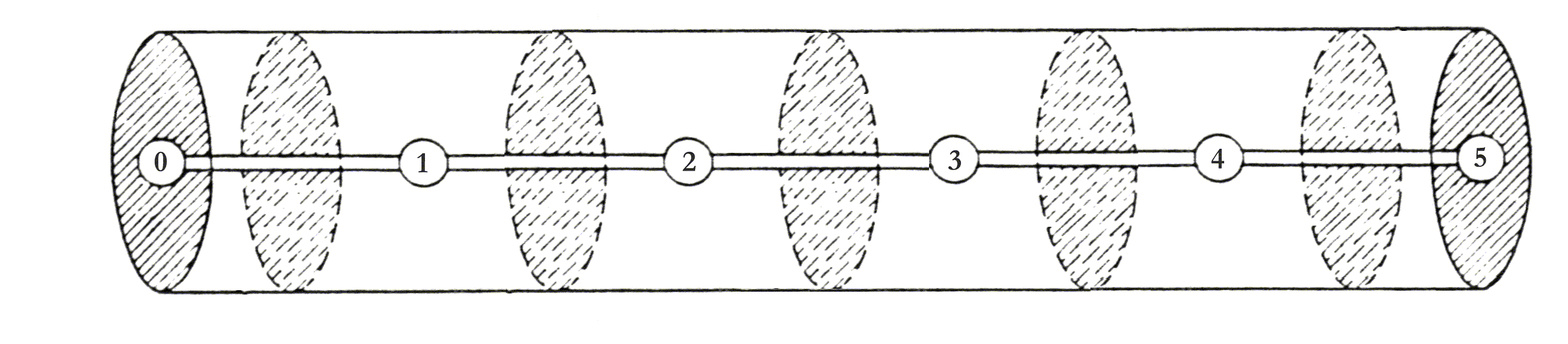
Figura 3-1
: barretta suddivisa da sei nodi numeratipartendo da zero. Si notano le barrette conduttrici
e la serie di sottovolumi.
Preliminarmente, si discretizza nello spazio lo spessore della nostra lastra, sostituendo al dominio continuo una serie di punti discreti in esso contenuti. In pratica, dividiamo la lastra in una serie di fette, o sottovolumi, supponendoli ognuno a temperatura uniforme uguale a quella del loro punto centrale. Si sostituisce così il sistema con una serie di barre fittizie conduttrici di calore che collegano ogni fetta della lastra tramite il suo centro, o meglio detto nodo. Tale rete di barre, prese con conduttanza uguale al materiale che attraversano, approssimano relativamente bene il flusso di calore nel sistema continuo.
Il primo nodo sarà preso esattamente su una delle due pelli della lastra, poi seguiranno gli altri, intermedi, tutti con eguale distanza D x (costante) dal precedente. Si arriverà così infine a determinare l’ultimo nodo sulla pelle opposta della lastra (vedi figura 3-1). Questa discretizzazione spaziale ci permette di affermare che la variabile x, anziché appartenere all’insieme dei numeri reali, è discreta ed è uguale a:
![]() (9)
(9)
nella quale D x viene chiamato passo spaziale, n invece, numero puro, viene chiamato indice di nodo (vedi figura 3-2). Tale indice viene convenzionalmente fatto partire da 0 o da 1.
In effetti, il problema del numero di partenza dal quale enumerare i nodi è storico, e la causa di ciò sono i linguaggi di programmazione. Questi, in passato, erano molto rigidi, e l’utilizzo dell’uno o dell’altro comportava l’adeguamento alle loro regole e alla loro sintassi. Per alcuni di essi il primo numero intero era l’uno, per altri lo zero, e ciò creava diversità nella trattazione dei problemi, risolvibili solamente da particolari linguaggi. Al giorno d’oggi tale problema è stato superato grazie alla maggiore versatilità degli strumenti digitali di calcolo, capaci di risolvere una vasta gamma di problemi fisici senza dover seguire regole troppo rigide.
In questa sede, comunque, si supporrà n partire da 0 fino a raggiungere N. Ciò significa che in realtà il numero di nodi sarà N+1, mentre il numero di divisioni sarà N:
![]()
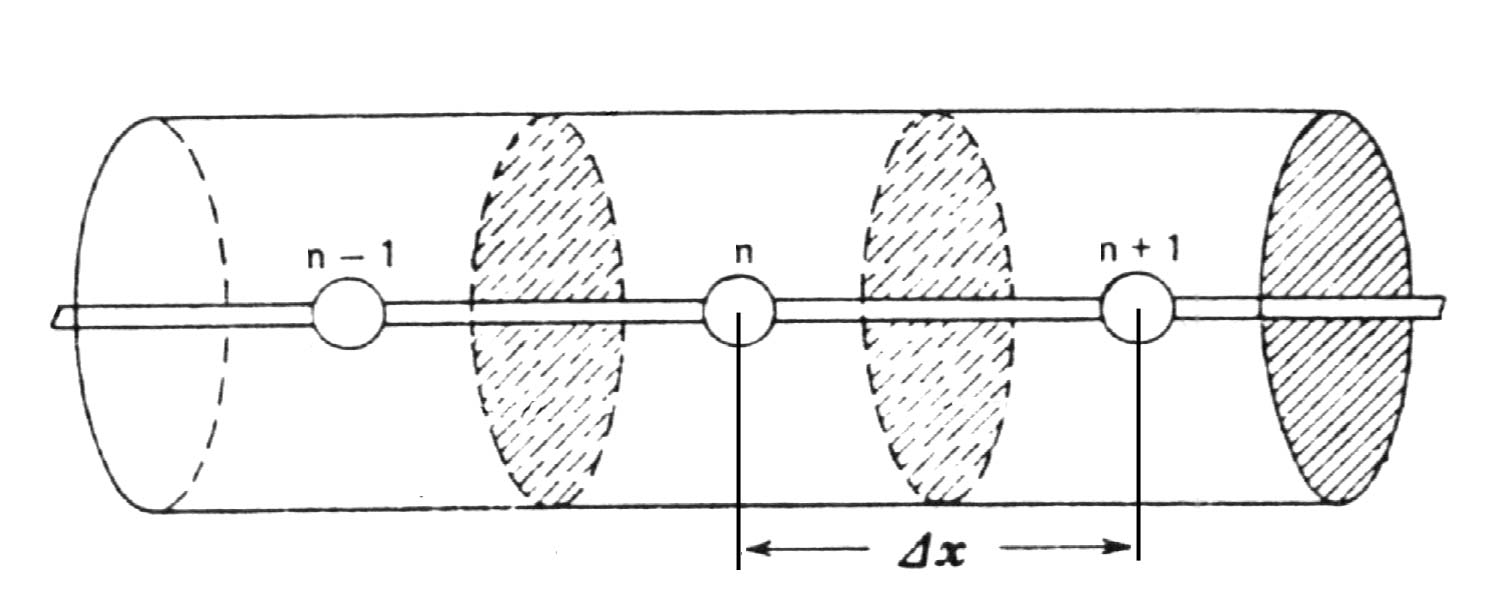
Figura 3-2
: rappresentazione del nodo ennesimo e dei suoiadiacenti in un’aletta circolare. Si noti il passo spaziale D x.
3.2 DISCRETIZZAZIONE DEL TEMPO
Ricordiamoci ora che stiamo studiando un transitorio, cioè un’evoluzione nel tempo del sistema. Ciò significa che in ciascun nodo della lastra la temperatura varierà col trascorrere del tempo.
Anche il tempo va quindi discretizzato, prendendo un opportuno intervallo temporale D t , chiamato correttamente passo temporale. La variabile t , a questo punto discreta, può essere individuata come:
![]() (10)
(10)
con t chiamato indice di tempo, anch’esso numero puro come n. Questo indice non ha però alcun limite superiore e varia come:
![]()
![]()
Questo poiché non esiste alcuna maniera pratica per fissare un limite di tempo che indichi la conclusione del transitorio. In generale comunque, il problema terminerà quando sarà stata raggiunta una situazione di regime.
3.3 L’EQUAZIONE DI FOURIER ALLE DIFFERENZE FINITE
Dobbiamo ora riscrivere l’equazione di Fourier alle differenze finite, cioè tramite le variabili discretizzate. Invece di procedere partendo dall’equazione stessa (cosa analiticamente corretta ma che ingegneristicamente s’usa poco) ricostruiamola già discretizzata. Ricordiamo quindi che essa non è altro che l’applicazione del primo principio termodinamico di un sistema chiuso in forma differenziale: il flusso di calore entrante o uscente da un volumetto del sistema produce una variazione dell’energia interna.
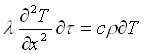
![]() (11)
(11)
Ciò perché il laplaciano di T si riduce alla derivata seconda rispetto a x, essendo il problema monodimensionale. Scriviamo pertanto la derivata nel tempo e nello spazio presenti nell’equazione utilizzando i rapporti incrementali.
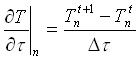 (12)
(12)
Cioè la derivata parziale rispetto al tempo della temperatura calcolata al nodo n è data dalla differenza tra la temperatura che si ha allo stesso nodo al tempo futuro t+1 e quella al tempo attuale t, divisa per il passo temporale. Questo basarsi sulle temperature al tempo futuro viene detto predittivo e risulta per i nostri scopi particolarmente confacente. Così facendo infatti saremo agevolmente in grado di dedurre le temperature future in base a quelle attuali con una semplice formula.
È possibile utilizzare anche un altro metodo, detto implicito, che verrà discusso più avanti nel paragrafo numero 5.
Usiamo dunque il metodo predittivo per calcolare la derivata della temperatura rispetto all’ascissa. Essa può essere scritta in due modi diversi, utilizzando cioè il nodo a destra o a sinistra dell’ennesimo.
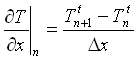 usando il nodo a destra. (13)
usando il nodo a destra. (13)
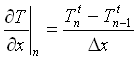 usando il nodo a sinistra. (14)
usando il nodo a sinistra. (14)
Poiché a noi interessa la derivata seconda, essa, applicando due volte l’approssimazione alle differenze finite, può essere scritta con la differenza delle derivate prime:
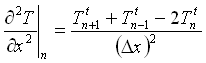 (15)
(15)
Possiamo pertanto scrivere l’equazione di Fourier alle differenze finite come:
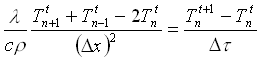 (16)
(16)
espressione algebrica grazie alla quale si riesce a trovare la temperatura del nodo n al tempo t+1. La nostra incognita è pertanto data dalla formula:
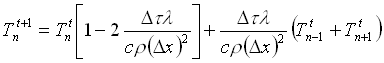 (17)
(17)
Questa formula permette di calcolare la temperatura del nodo n al tempo futuro, sapendo solo le temperature al tempo attuale del nodo stesso e di quelli immediatamente adiacenti ad esso.
Normalmente in questo tipo di problemi è nota la temperatura iniziale della lastra, uniforme e pari a ![]() in ogni nodo. La lastra viene poi immersa in un bagno e nell’istante di tempo successivo la pelle si porta alla temperatura imposta dal bagno stesso. Comincia così il transitorio che può essere risolto tramite il cosiddetto time marching, ovverosia tramite il trovare, dal tempo attuale, le temperature al tempo successivo. Iterando il ragionamento fino ad una situazione di regime si raggiunge la soluzione del problema.
in ogni nodo. La lastra viene poi immersa in un bagno e nell’istante di tempo successivo la pelle si porta alla temperatura imposta dal bagno stesso. Comincia così il transitorio che può essere risolto tramite il cosiddetto time marching, ovverosia tramite il trovare, dal tempo attuale, le temperature al tempo successivo. Iterando il ragionamento fino ad una situazione di regime si raggiunge la soluzione del problema.
3.4 IL PASSO TEMPORALE LIMITE E OTTIMALE
La soluzione tramite time marching, detta di tipo esplicito (causa l’esplicitazione dell’incognita nella formula risolutiva stessa), ha però un difetto. Essa in pratica pone un limite al rapporto
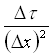 (18)
(18)
poiché esso governa il segno del termine, nella formula (17) :
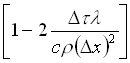 (19)
(19)
Se tale termine diventa negativo si pone infatti un serio problema di contraddizione con il principio zero e il secondo principio della termodinamica. Supponiamo per un istante che i due nodi adiacenti siano a temperatura più alta dell’ennesimo. Ci si aspetterebbe, per i principi suddetti, che la temperatura di tale nodo cresca. Tuttavia, causa il segno negativo del termine prima evidenziato, la temperatura del nodo n, invece di salire, diminuisce: ciò significa che il calore è fluito spontaneamente da un corpo freddo ad uno più caldo!
In questo caso il problema viene definito numericamente instabile. In effetti ciò che succede è che il discriminante dell’equazione differenziale a cui è associata l’equazione da noi considerata, è diventato negativo. Come conseguenza di ciò si hanno come soluzione due radici complesse coniugate; le soluzioni esponenziali dell’equazione differenziale diventano pertanto, sviluppate con Eulero, una somma di seni e coseni, dando origine a fenomeni oscillanti.
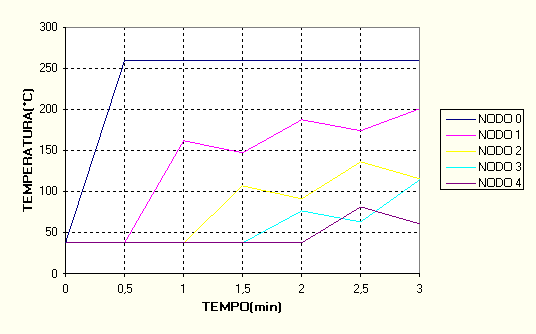
Figura 3-3
: fenomeni oscillanti nelle temperature dei nodi di una lastra a 38°Cimmersa nell’olio a 260°C. Il D t è stato preso come 30s.
Graficamente, nel nostro caso tale oscillazione si vede chiaramente nella temperatura di nodi generici, in figura 3-3.
Benché fisicamente esistano fenomeni di vibrazioni e corpi che oscillano nei quali è possibile una soluzione di questo tipo, in essi comunque rimane saldo il principio di conservazione dell’energia e pertanto, tali oscillazioni, tendono comunque a calare nel tempo. Ma se, come in questo caso, tali oscillazioni non si smorzano, allora si è in presenza di un fenomeno inaccettabile dal punto di vista energetico che viene appunto definito instabile.
Questo fa sì che utilizzando intervalli di tempo molto piccoli si debba comunque prendere un passo spaziale ridotto con una conseguente mole di calcoli elevata. Viceversa, prendendo intervalli D x ridotti per aumentare la precisione, sono costretto a utilizzare un passo temporale dell’ordine dei nanosecondi, allungando spaventosamente il tempo di calcolo.
Viene quindi definito il concetto di passo temporale limite, cioè il valore che annulla il termine tra parentesi quadre nell’equazione risolutiva:
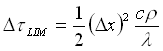 (20)
(20)
e ricordando la definizione di diffusività termica (che risulta, quindi, grandezza fondamentale nel governare il transitorio) diventa:
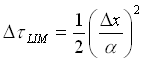 (21)
(21)
e l’equazione risolutiva, scegliendo come passo temporale quello limite, diventa:
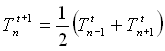 (22)
(22)
Ciò significa che posso esprimere la temperatura al tempo t+1 del nodo ennesimo come la media aritmetica delle temperature al tempo t dei due nodi adiacenti. Tuttavia questo comporta un andamento nel tempo della temperatura di nodo n con bruschi salti (vedi figura 3-4). Questi gradini sono dovuti al fatto che siamo al limite dell’inizio dei fenomeni oscillanti.
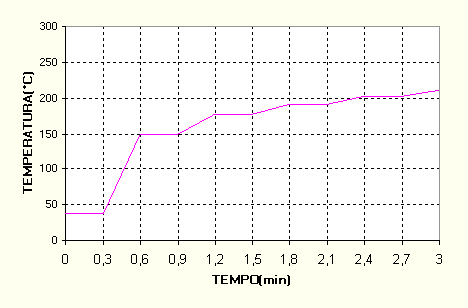
Figura 3-4
: temperatura di nodo calcolata con D t limite.Si usa definire perciò anche un passo temporale ottimale come:
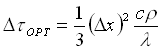 (23)
(23)
che quindi è esattamente 2/3 di quello limite. In altre parole, il numero di passi ottimali è una volta e mezzo quelli limite. Usando il passo temporale ottimale la formula risolutiva diventa:
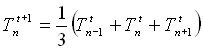 (24)
(24)
Con una formula molto semplice ed un aggravio di calcoli decisamente trascurabile si riesce ad ottenere quella che si definisce soluzione ottima del problema. Come si può vedere in figura 3-5 ora la temperatura di nodo sale più gradualmente, senza gradini né salti eccessivi.
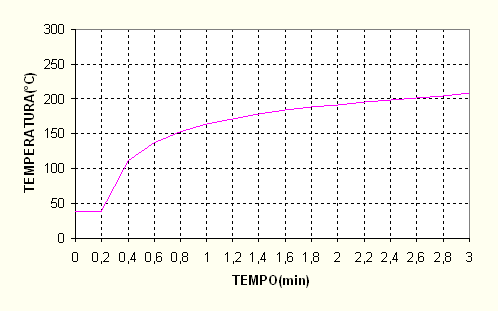
Figura 3-5
: temperatura di nodo calcolata con D t ottimale.3.5 ESEMPIO DI CALCOLO
Supponiamo di avere una piastra infinita di spessore 120 mm, con diffusività ![]() pari a 0,023
pari a 0,023 ![]() . Al tempo t
= 0, uniforme su tutto il volume, la temperatura della lastra
. Al tempo t
= 0, uniforme su tutto il volume, la temperatura della lastra ![]() è 38°C. Si supponga poi di immergere la lastra nell’olio alla temperatura
è 38°C. Si supponga poi di immergere la lastra nell’olio alla temperatura ![]() di 260°C. Il nostro scopo è calcolare T(x,t
) nei primi tre minuti.
di 260°C. Il nostro scopo è calcolare T(x,t
) nei primi tre minuti.
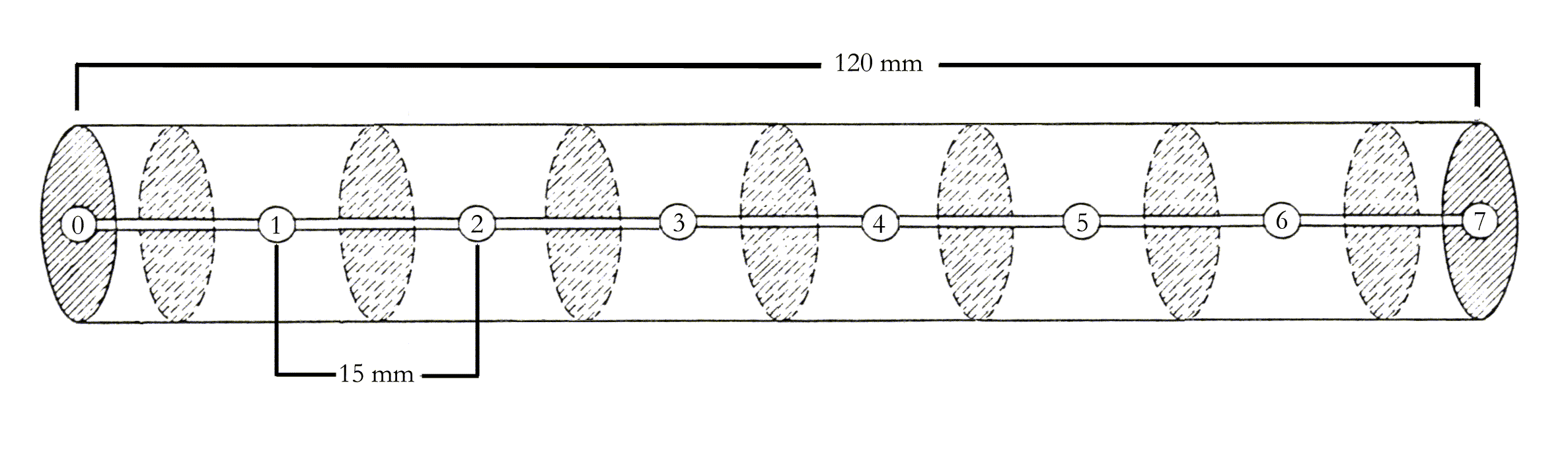
Figura 3-6
: discretizzazione della lastra. Sono presenti 8 nodi.Innanzitutto si noti che il problema è simmetrico. Entrambe le pelli della lastra, infatti, vengono a contatto con l’olio e raggiungono al primo intervallo temporale la temperatura del liquido. È possibile quindi studiare metà della lastra.
Il primo passo da compiere è la discretizzazione della lastra stessa; prendiamo dunque, ad esempio, 8 nodi (vedi figura 3-6). Si avrà pertanto un passo spaziale uguale a:
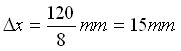
Volendo utilizzare il passo temporale limite esso sarà:
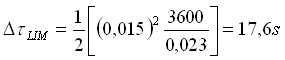
vale a dire circa 0,3 minuti. Avremo dunque 11 intervalli di tempo (contando l’istante 0) in cui calcolare le temperature dei nodi di metà lastra.
Ora si può costruire il tabulato che riporta tutte le temperature dei nodi, tenendo presente che la temperatura del nodo ennesimo al tempo t+1 è la media aritmetica delle temperature dei nodi adiacenti al tempo precedente t. Nella figura 3-7 è riportata la tabella del problema, costruita semplicemente come foglio di Excel.
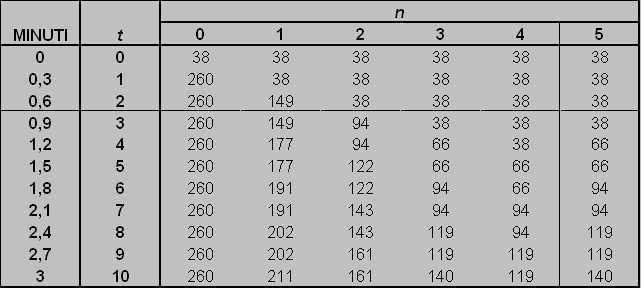
Figura 3-7
: la tabella, costruita con Excel, riporta le temperature dei nodi di metà lastra adogni intervallo temporale.
Si nota quindi che per t uguale a:
0. la temperatura è 38°C ovunque, essendo la lastra a temperatura ambiente.
1. la lastra è immersa nell’olio e la pelle si porta istantaneamente a 260°C.
2. il calore inizia a diffondersi nella lastra partendo dal nodo adiacente alla pelle.
3. si noti che il secondo nodo è rimasto alla temperatura del tempo precedente. È salito invece il terzo nodo.
4. ora sale il nodo 2, mentre rimangono alla stessa temperatura quelli a lui adiacenti. In effetti tale fenomeno si avrà anche per gli istanti successivi, come se i nodi della lastra salissero di temperatura "incrociando" i loro percorsi.
Si riporta ora il grafico delle temperature dei nodi per consentire un’agevole riscontro dei risultati:
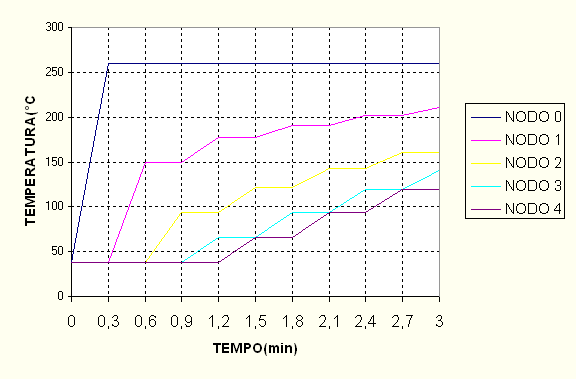
Figura 3-8
: grafico riportante le temperature di tutti i nodi.Si notino i bruschi salti e l’andamento "incrociato"
Il fenomeno descritto in precedenza causa un errore di discretizzazione ad ogni passaggio del time marching. Questo fa sì che la tecnica del metodo numerico sia imprecisa se sviluppata per lassi di tempo piuttosto lunghi, mentre sia affidabile in casi come il nostro problema, dove si è cercato di calcolare le temperature dei nodi della lastra solo nei tre minuti successivi alla sua immersione nell’olio. In figura 3-8 è descritta la variazione di temperatura dei nodi. Si possono notare i bruschi salti già evidenziati in precedenza.
Con questo il nostro problema è risolto. La sua soluzione però è fortemente caratterizzata da tutti quei limiti che sono già stati evidenziati.
Ovviamente la soluzione trovata sarebbe stata molto più accurata se invece del passo temporale limite avessimo scelto quello ottimale. Se si provasse, mantenendo inalterati tutti i dati del problema, a ricostruire la tabella, questa diventerebbe quella di figura 3-9, più pesante ma molto più soddisfacente.
Per costruirla si è calcolato:
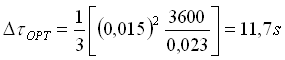
cioè circa 0,2 minuti. Il numero di intervalli è, come si vede, una volta e mezzo quelli limite. Si nota immediatamente dai valori immessi che i gradini visti in precedenza sono in questo caso spariti, come si può riscontrare anche in figura 3-10. Con una quantità di calcoli trascurabile siamo così giunti ad una soluzione ben più precisa della precedente.
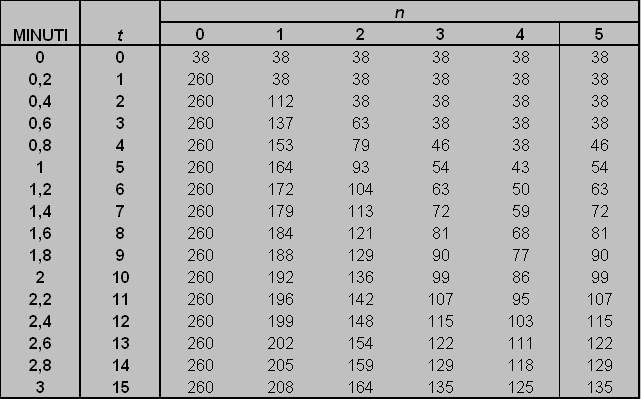
Figura 3-9: tabella ricostruita partendo dal passo temporale ottimale.
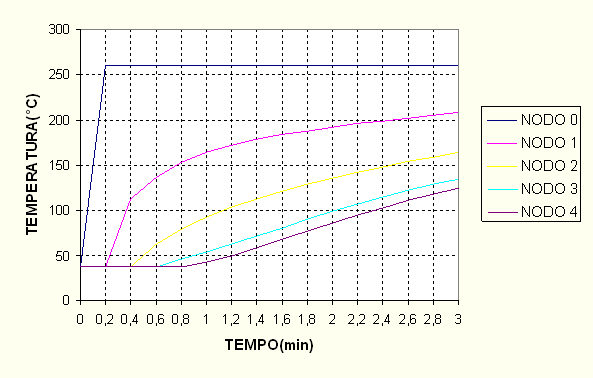
Figura 3-10
: grafico dei valori di temperatura ai nodi. Si nota che lecurve sono senza salti né tratti orizzontali. È sparito l’andamento
"incrociato".
4. PROGRAMMI ALL’ELABORATORE
Con le semplici basi di teoria finora presentate e un’infarinatura di un qualsiasi linguaggio di programmazione sarebbe già possibile creare un semplice programma capace di risolvere il problema citato nel capitolo precedente.
Sono di seguito riportati, a titolo di esempio, due listati di programmi in qbasic, stesi da studenti dell’Università di Parma qualche anno fa (1992). Sebbene il linguaggio di programmazione sia obsoleto è possibile rendersi conto di quale sia la semplicità di tali programmi e con quale facilità essi risolvano il problema che è stato posto. Sono in ogni modo programmi ad uso proprio il cui scopo non era quello di essere letti da un pubblico di persone, e perciò poco commentati.
NOME FILE : TRANSTRM.BAS
DEFDBL A-Z
DECLARE SUB graf ()
DECLARE SUB disp ()
DECLARE FUNCTION sy (y)
DECLARE FUNCTION sx (x)
DIM SHARED s, alfa, Nd, ts, td, tzero
DIM SHARED dx, dt, ymin, ymax, fl, tempo
fl = 1
COLOR 15, 0, 1
CLS
INPUT "Spessore lastra (mm)"; s
s = s / 1000' converto in m
INPUT "diffusivita' (m/sý)"; alfa
INPUT "numero divisioni "; Nd
INPUT "Temp. par. sx (øC)"; ts
INPUT "Temp. par. dx (øC)"; td
INPUT "Temp. iniziale (øC)"; tzero
dx = s / Nd
dt = 1 / 2 / alfa * dx * dx
PRINT "interv. temporale limite dt="; dt; "s"
INPUT "nuovo intervallo temporale "; nint
IF nint <> 0 THEN dt = nint
INPUT "Quanti intervalli vuoi vedere "; Ninterv
PRINT "premi un tasto"
DO: LOOP UNTIL LEN(INKEY$) > 0
CALL graf
Np1% = Nd + 1
DIM SHARED t(1 TO Np1%, 150)
t(1, 0) = ts
t(Np1%, 0) = td
FOR i = 2 TO Nd
t(i, 0) = tzero
NEXT
cost = dt * alfa / dx ^ 2
FOR tempo = 0 TO Ninterv
t(1, tempo + 1) = t(1, tempo)
t(Np1%, tempo + 1) = t(Np1%, tempo)
FOR i = 2 TO Nd
t(i, tempo + 1) = t(i, tempo) * (1 - 2 * cost) + (t(i - 1, tempo) + t(i + 1, tempo)) * cost
NEXT i
FOR j = 1 TO 2000: NEXT ' ciclo di rallentamento visualizzazione
CALL disp
NEXT tempo
END
SUB disp
IF tempo > 0 THEN
FOR i = 2 TO Nd + 1
LINE (sx(i - 2), sy(t(i - 1, tempo - fl)))-(sx(i - 1), sy(t(i, tempo - fl))), 0
NEXT
END IF
LOCATE 1, 1: PRINT "tempo" + LEFT$(STR$(tempo * dt) + " ", 8) + " s "
FOR i = 2 TO Nd + 1
LINE (sx(i - 2), sy(t(i - 1, tempo)))-(sx(i - 1), sy(t(i, tempo))), 12
NEXT
END SUB 'disp
SUB graf
DIM dat%(10000)
SCREEN 12
CLS 0
ymin = ts
IF td < ts THEN ymin = td
IF tzero < ymin THEN ymin = tzero
ymax = ts
IF td > ts THEN ymax = td
IF tzero > ymax THEN ymax = tzero
LINE (40, sy(tzero))-(600, sy(tzero))
LINE (40, sy(tzero))-(40, sy(ts))
LINE (40, sy(ts))-(36, sy(ts))
LINE (40, sy(tzero))-(36, sy(tzero))
LINE (40, sy(td))-(36, sy(td))
LINE (600, sy(tzero))-(600, sy(td))
LINE (600, sy(td))-(605, sy(td))
LOCATE 1, 1: PRINT tzero: GET (0, 0)-(31, 15), dat%(0)
PUT (1, sy(tzero) - 7), dat%(0), OR
LOCATE 1, 1: PRINT " "
LOCATE 1, 1: PRINT ts: GET (0, 0)-(31, 15), dat%(0)
PUT (1, sy(ts) - 7), dat%(0), OR
LOCATE 1, 1: PRINT " "
LOCATE 1, 1: PRINT td: GET (0, 0)-(31, 15), dat%(0)
PUT (1, sy(td) - 7), dat%(0), OR
LOCATE 1, 1: PRINT " "
END SUB 'graf
FUNCTION sx (x)
sx = 40 + 560 * x / Nd
END FUNCTION
FUNCTION sy (y)
sy = 450 - 400 * (y - ymin) / (ymax - ymin)
END FUNCTION
DEFINT I-N, T
SUB vecmult (a() AS DOUBLE, TT() AS DOUBLE, N, t)
FOR i = 1 TO N
TT(i, t + 1) = 0
FOR j = 1 TO N
TT(i, t + 1) = TT(i, t + 1) + a(i, j) * TT(j, t)
NEXT j
NEXT i
END SUB
Questo primo programma permette di variare lo spessore della lastra, il numero di nodi, la temperatura iniziale e tutte le condizioni al contorno, ammettendo casi anche non simmetrici. Viene poi calcolato il D t limite e chiesto se si vuole inserire un nuovo intervallo temporale differente. graf è la subroutine che mostra il grafico della temperatura in ogni istante. Il cuore del programma è il ciclo for nel quale vengono calcolate tutte le temperature in ogni istante: quelle sulle due pelli rimangono quelle imposte dalle condizioni al contorno, quelle dei nodi interni vengono trovate attraverso la formula risolutiva vista nel capitolo 3. Infine viene chiamata la subroutine disp che visualizza i risultati ottenuti.
Ecco un altro esempio di listato:
NOME FILE : TRANSTR2.BAS
defdbl a-z
DECLARE SUB graf ()
DECLARE SUB disp ()
DECLARE FUNCTION sy (Y)
DECLARE FUNCTION sx (X)
DECLARE SUB vecmult (A() AS DOUBLE, TT() AS DOUBLE, N%, T%)
DIM SHARED s, alfa, Nd, ts, td, tzero
DIM SHARED DX, dt, YMIN, YMAX, fl, tempo%
fl = 1
COLOR 15, 0, 1
CLS
INPUT "Spessore lastra (mm)"; s
s = s / 1000' converto in m
INPUT "diffusivita' (m/sý)"; alfa
INPUT "numero divisioni "; Nd
INPUT "Temp. par. sx (øC)"; ts
INPUT "Temp. par. dx (øC)"; td
INPUT "Temp. iniziale (øC)"; tzero
DX = s / Nd
dt = 1 / 2 / alfa * DX * DX
PRINT "interv. temporale limite dt="; dt; "s"
INPUT "nuovo intervallo temporale "; NINT
IF NINT <> 0 THEN dt = NINT
INPUT "Quanti intervalli vuoi vedere "; Ninterv
PRINT "premi un tasto"
DO: LOOP UNTIL LEN(INKEY$) > 0
CALL graf
Np1% = Nd + 1
DIM SHARED T(1 TO Np1%, 150)
DIM A(1 TO Np1%, 1 TO Np1%)
DIM Y(1 TO Np1%, 1 TO Np1%)
' riempimento della matrice A
cost = dt * alfa / DX ^ 2
A(1, 1) = 1
FOR I = 2 TO Np1% - 1
A(I, I) = 1 + 2 * cost
A(I, I - 1) = -cost
A(I, I + 1) = -cost
NEXT
A(Np1%, Np1%) = 1
' inversione della matrice A
CALL MATINV(A(), Y(), Np1%)
' ora Y() contiene l' inversa di A
' condizione iniziale
T(1, 0) = ts
T(Np1%, 0) = td
FOR I = 2 TO Nd
T(I, 0) = tzero
NEXT
FOR tempo% = 0 TO Ninterv
CALL vecmult(Y(), T(), Np1%, tempo%)
CALL disp
FOR j% = 1 TO 2000: NEXT ' ciclo di rallentamento visualizzazione
NEXT tempo%
END
SUB disp
IF tempo% > 0 THEN
FOR I = 2 TO Nd + 1
LINE (sx(I - 2), sy(T(I - 1, tempo% - fl)))-(sx(I - 1), sy(T(I, tempo% - fl))), 0
NEXT
END IF
LOCATE 1, 1: PRINT "tempo" + LEFT$(STR$(tempo% * dt) + " ", 8) + " s "
FOR I = 2 TO Nd + 1
LINE (sx(I - 2), sy(T(I - 1, tempo%)))-(sx(I - 1), sy(T(I, tempo%))), 12
NEXT
END SUB 'disp
SUB graf
DIM DAT%(10000)
SCREEN 12
CLS 0
YMIN = ts
IF td < ts THEN YMIN = td
IF tzero < YMIN THEN YMIN = tzero
YMAX = ts
IF td > ts THEN YMAX = td
IF tzero > YMAX THEN YMAX = tzero
LINE (40, sy(tzero))-(600, sy(tzero))
LINE (40, sy(tzero))-(40, sy(ts))
LINE (40, sy(ts))-(36, sy(ts))
LINE (40, sy(tzero))-(36, sy(tzero))
LINE (40, sy(td))-(36, sy(td))
LINE (600, sy(tzero))-(600, sy(td))
LINE (600, sy(td))-(605, sy(td))
LOCATE 1, 1: PRINT tzero: GET (0, 0)-(31, 15), DAT%(0)
PUT (1, sy(tzero) - 7), DAT%(0), OR
LOCATE 1, 1: PRINT " "
LOCATE 1, 1: PRINT ts: GET (0, 0)-(31, 15), DAT%(0)
PUT (1, sy(ts) - 7), DAT%(0), OR
LOCATE 1, 1: PRINT " "
LOCATE 1, 1: PRINT td: GET (0, 0)-(31, 15), DAT%(0)
PUT (1, sy(td) - 7), DAT%(0), OR
LOCATE 1, 1: PRINT " "
END SUB 'graf
FUNCTION sx (X)
sx = 40 + 560 * X / Nd
END FUNCTION
FUNCTION sy (Y)
sy = 450 - 400 * (Y - YMIN) / (YMAX - YMIN)
END FUNCTION
DEFINT I-N, T
SUB vecmult (A() AS DOUBLE, TT() AS DOUBLE, N, T)
FOR I = 1 TO N
TT(I, T + 1) = 0
FOR j = 1 TO N
TT(I, T + 1) = TT(I, T + 1) + A(I, j) * TT(j, T)
NEXT j
NEXT I
END SUB
L’unica differenza dal programma precedente è che qui si utilizza il metodo implicito, che sarà ampiamente trattato nel prossimo capitolo. Si consiglia pertanto di rivedere tale programma dopo la lettura del suddetto.
Con il perfezionamento dei linguaggi di programmazione sarebbe ora possibile scrivere queste istruzioni in poche righe, includendo un sensibile miglioramento dell’interfaccia grafica. Ciò non significa però che gli strumenti moderni siano più semplici di quelli sorpassati. In visual basic questi programmi risulterebbero senza dubbio più "friendly" per l’utente, ma sarebbero d’altra parte molto più onerosi da scrivere.
Un buon compromesso è rappresentato da Excel, di cui già in precedenza si è accennato: la sua rudezza d’approccio combinata ad un’eccellente visualizzazione ne fa uno strumento assai potente per i nostri scopi. Esso ha raggiunto una potenza che non ha molto da invidiare a matlab e può essere usato con profitto per risolvere questi tipi di calcoli, creando tabelle e grafici con poco dispendio di tempo (vedi il capitolo precedente) e un’ottima interfaccia utente.
5. LA FORMULAZIONE IMPLICITA
È possibile evitare il problema del passo temporale limite e delle oscillazioni nelle temperature dei nodi semplicemente ricorrendo alla formulazione implicita.
L’unica differenza con il metodo predittivo consiste nello scrivere la derivata temporale. Se prima si utilizzava la temperatura del nodo n all’istante di tempo successivo a t, ora si utilizzerà quella all’istante di tempo precedente. In pratica:
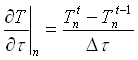 (25)
(25)
L’equazione di Fourier alle differenze finite dovrà dunque essere scritta come:
![]()
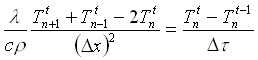 (26)
(26)
Ma in questa equazione sono presenti tre incognite, ovverosia le tre temperature al tempo t che si cerca di calcolare in funzione del tempo precedente t-1.
Per risolverla si è costretti a scrivere la medesima equazione per tutti gli n nodi, ottenendo così un sistema di n equazioni in n incognite. Infatti la temperatura al tempo t del nodo ennesimo compare in tre equazioni: in una come nodo centrale, nelle altre due come nodo adiacente di destra e di sinistra.
Il sistema è dunque algebrico lineare che in forma matriciale può essere scritto come:
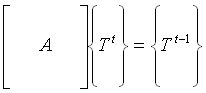 (27)
(27)
dove le temperature incognite al tempo presente costituiscono un vettore n x 1, così come i termini noti (ovvero le temperature vecchie) . La matrice A è quadrata, più precisamente n x n, tridiagonale e simmetrica. Infatti in ogni equazione compaiono solo il nodo centrale e i suoi adiacenti e pertanto tutti gli altri coefficenti risultano essere 0. In corrispondenza della riga k-esima si ha quindi:
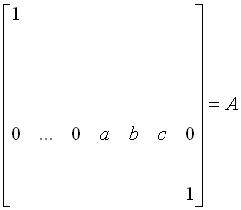
I coefficenti 1 sulla prima e l’ultima riga sono dovuti al fatto che i nodi sulle due pelli non cambiano mai temperatura, ma rimangono sempre a quella imposta dalle condizioni al contorno. Si ha cioè:
![]() (29)
(29)
che vale anche per l’ennesimo e ultimo nodo. I tre termini diversi da zero di ogni riga sono ottenibili mettendo in evidenza nell’equazione di Fourier i coefficenti delle temperature al tempo presente:
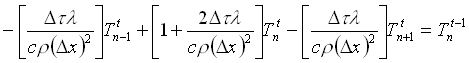 (30)
(30)
L’equazione così definita viene detta in forma normale. Si riconoscono così i tre coefficenti indicati con a, b e c nella formula (28):
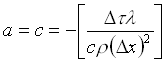 (31)
(31)
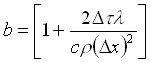 (32)
(32)
e la matrice si riconosce facilmente essere simmetrica. Si noti inoltre che in questo caso il termine b non può essere negativo, escludendo così ogni problema riguardo al limite del passo temporale utilizzabile nell’analisi.
A questo punto è possibile risolvere il problema semplicemente invertendo la matrice A e ottenendo il sistema in forma matriciale:
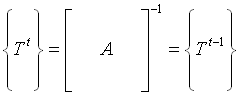 (33)
(33)
Si può vedere la matrice A come un filtro che, convoluto con il vettore delle temperature al tempo precedente, dà come risultato il vettore delle temperature al tempo presente. L’inversione della matrice è fondamentale perché in tal modo si ottiene facilmente il risultato per ogni istante di tempo senza eccessivi calcoli.
Il grande vantaggio di questo metodo rispetto al precedente, risiede nel fatto che qualunque passo temporale si scelga di utilizzare per l’analisi del problema, i grafici delle temperature dei nodi in funzione del tempo non avranno mai salti e bruschi gradini, né si correrà il rischio di violare alcun principio della termodinamica.
![]()
![]()