
Esercizi sullo scambio termico per irraggiamento
Esercizio 1
Testo
Dato un forno cilindrico, rotante, per la cottura del cemento, di lunghezza 5 m, diametro 1.5 m, con temperatura di parete 523 K, coefficiente di assorbimento 0.8, calcolare la potenza termica dispersa per irraggiamento dal forno.
E' nota, inoltre, la temperatura ambiente di 300 K
Dati

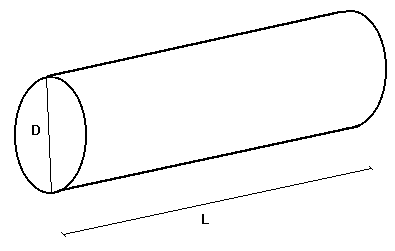
Figura 1 - Forno Rotante
Richiesti
![]() (Potenza termica dispersa dal forno per irraggiamento per unità di tempo)
(Potenza termica dispersa dal forno per irraggiamento per unità di tempo)
Risoluzione
Il problema è il caso limite di scambio termico per irraggiamento tra due corpi, uno convesso contenuto in uno concavo, in cui la superficie del corpo contenitore è molto più grande di quella del corpo contenente e perciò ![]() (
( ![]() fattore di forma, con A: ambiente esterno, F: forno)
fattore di forma, con A: ambiente esterno, F: forno)
Posso utilizzare quindi la formula semplificata.
Indico con
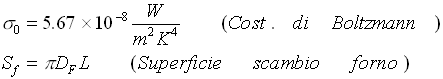
Quindi
![]()
E' un valore eccessivo per un buon rendimento del forno!
Viene deciso perciò di isolare il forno tramite l'installazione di un tubo coassiale ad esso, di lamiera lucida zincata, che funge da schermo metallico.
Il diametro dello schermo è 1.5 volte quello del forno.
E' dato inoltre il coefficiente di assorbimento dello schermo.
Mi domando, ora, di quanto si è ridotto lo scambio termico per irraggiamento tra forno e ambiente esterno.
Dati aggiunti
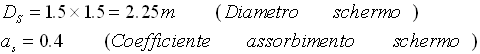
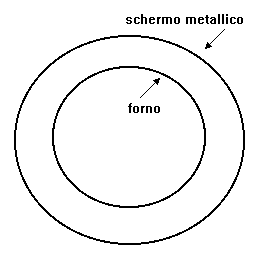
Figura 2 - Forno e Schermo in sezione
Richiesti aggiunti
![]() (potenza termica dispersa per irraggiamento, per unità di tempo, dal
(potenza termica dispersa per irraggiamento, per unità di tempo, dal
forno in presenza dello schermo)
Risoluzione
Con l'installazione dello schermo, lo scambio termico per irraggiamento del forno con l'esterno diminuisce.Infatti il "salto" di temperatura è diviso in due parti: dal forno allo schermo e dallo schermo all'esterno; poiché la dipendenzadella potenza termica dalla temperatura è quartica, lo scambio totale diminuisce.
Indico con
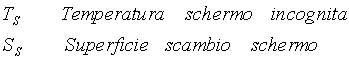
A regime la potenza termica scambiata tra il forno e lo schermo è la stessa scambiata tra schermo e ambiente esterno. Perciò calcolo ![]() in due modi:
in due modi:
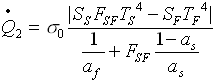
Poichè il forno è un corpo convesso, 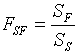
Perciò sostituendo si ha
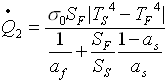 (1) equazione nelle due incognite
(1) equazione nelle due incognite ![]()
2) Come potenza scambiata tra schermo e ambiente esterno per unità di tempo. Essendo la superficie dell’ambiente esterno molto più grande di quella dello schermo, posso usare la formula semplificata:
![]() (2) equazione nelle due incognite
(2) equazione nelle due incognite ![]()
Quindi uguaglio le due espressioni per ricavare ![]() e quindi
e quindi ![]()
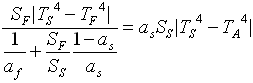
![]()
Essendo inoltre
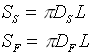 si ha
si ha
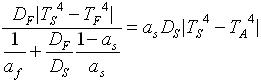
e quindi, togliendo i moduli, dopo aver tenuto conto che ![]()
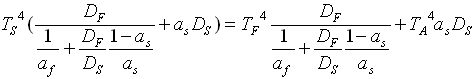
Sostituendo i simboli con i rispettivi valori numerici, ottengo:
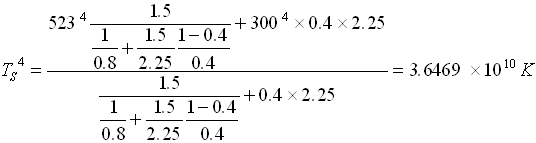
![]()
Ricavo ora ![]() dalla relazione (2), essendo più semplice
dalla relazione (2), essendo più semplice
![]()
Quindi l’installazione dello schermo ha prodotto una riduzione della dispersione del calore del 32% circa.
( infatti ![]() )
)
Inoltre dal punto di vista conduttivo e convettivo la presenza dello schermo non ha effetti particolari.
Il risultato di questo esercizio si può generalizzare affermando che, allo scopo di diminuire lo scambio termico per irraggiamento di un corpo, è utile rivestire il corpo stesso di uno schermo lucido.
Le navi spaziali e le tute degli astronauti sono infatti di materiale lucido, proprio per evitare enormi escursioni termiche, dannose sia per il corpo umano che per le parti meccaniche (dilatazione, ecc.)
Esercizio 2
Questo è l’ampliamento di un esercizio svolto il 14/12/98, in cui, nello svolgimento del suddetto, non si era tenuto conto del fenomeno dell’irraggiamento termico
Testo
E’ dato un tubo d’acciaio, di cui sono noti i raggi interno ed esterno, rivestito di uno strato di materiale isolante di cui è noto il raggio.
All’interno del tubo scorre acqua ad una temperatura e ad un grado igrometrico noti.
Si conosce inoltre il coefficiente di assorbimento dell’isolante, la sua conducibilità termica, il coefficiente di convezione interno ed esterno.
Si domanda se, tenendo conto anche del fenomeno dell’irraggiamento termico, il raggio dell’isolante determinato in precedenza è ancora efficace per evitare la formazione di rugiada.
Dati

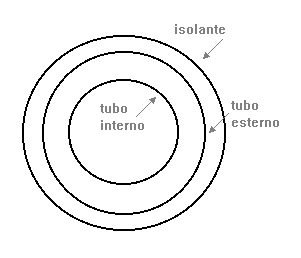
Figura 3 - Tubo e Isolante in sezione
Richiesti
![]()
Risoluzione
Lavoriamo per unità di lunghezza
Indico con

Dal diagramma psicrometrico, tenendo conto di ![]() e di
e di ![]() avevamo trovato che, per evitare la formazione di rugiada, la temperatura della parete esterna dovesse essere maggiore di 9°C.
avevamo trovato che, per evitare la formazione di rugiada, la temperatura della parete esterna dovesse essere maggiore di 9°C.
Assumo quindi la temperatura di parete esterna
![]()
La rete di resistenze calcolata era di questo tipo:
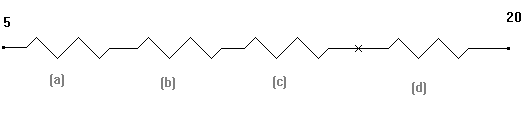
con:
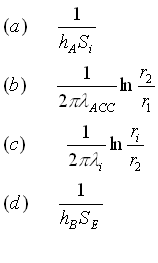
Indico con:
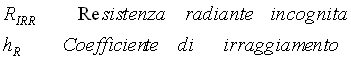
![]() Potenza termica scambiata per irraggiamento per unità di tempo e di superficie
Potenza termica scambiata per irraggiamento per unità di tempo e di superficie
Visto che le prime due resistenze erano state già calcolate, nella rete successiva le posso trascurare.
Nella nuova rete, per tener conto dell’effetto dell’irraggiamento termico, è necessario mettere in serie la resistenza conduttiva con il parallelo tra quella convettiva e quella radiante, ottenendo perciò:
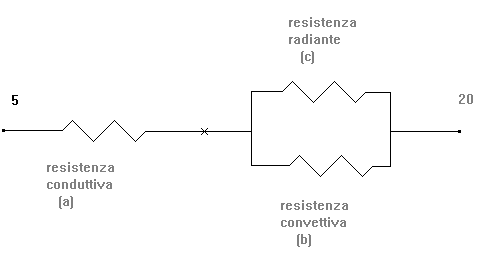
con:
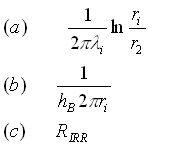
Posso scrivere la potenza ![]() scambiata per irraggiamento in due modi:
scambiata per irraggiamento in due modi:
1) Linearmente come 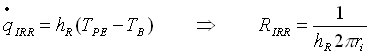
2) Usando la formula semplificata per l’irraggiamento (non lineare):
![]()
Dalla definizione di coefficiente di irraggiamento:
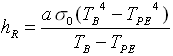
Sostituendo numericamente si ha:
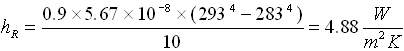
Facendo la composizione delle due resistenze in parallelo per ridurle a una sola:
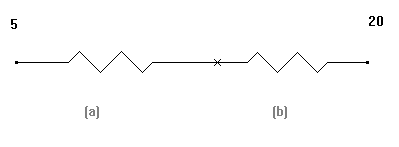
con:

Sostituendo con valori numerici:
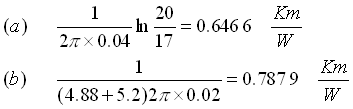
La resistenza totale ![]() sarà:
sarà:
![]()
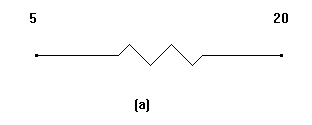
con :
![]()
Indico con ![]()
![]()
Per trovare ![]() :
:
![]()
Quindi il raggio dell’isolante determinato nell’esercizio precedente è ancora valido, essendo la nuova temperatura di parete ancora maggiore di 10°C.
Esercizio 3
Testo
Una mattonella lunga 0.5m , appoggiata su un materiale isolante ( ad esempio lana), è esposta ai raggi solari, inclinati di un angolo di 30° rispetto alla verticale.
L’aria è ferma e alla temperatura di 20°C.
La potenza termica emanata dal sole per unità di tempo e di superficie è ![]() .
.
E’ noto inoltre il coefficiente di assorbimento della mattonella.
Si domanda qual è l'incremento di temperatura della mattonella (per unità di tempo).
Dati

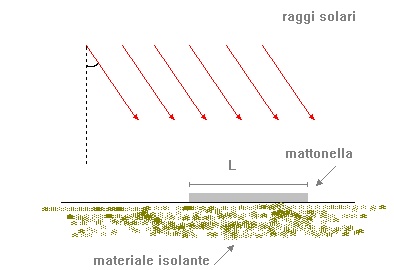
Figura 4 - Mattonella colpita dai raggi solari
Richiesti
![]()
Risoluzione
Dall’esperienza possiamo supporre che la mattonella si porterà ad una temperatura superiore di quella dell’aria (d’estate le pietre sotto ai nostri piedi scottano).
Indico con

![]() Potenza termica scambiata tra la mattonella e l’ambiente esterno
Potenza termica scambiata tra la mattonella e l’ambiente esterno
Dalle relazioni cateto-ipotenusa per un triangolo rettangolo:
![]()
Mi domando qual è la parte di potenza incidente la mattonella che viene assorbita.
![]()
Inoltre la potenza termica assorbita è pari a quella scambiata; la potenza termica viene scambiata in due modi:
1) Tramite convezione con l’ambiente esterno a 20°C
2) Tramite irraggiamento con l’ambiente esterno a 20°C
Per cui
![]() (1)
(1)
con incognite ![]()
e 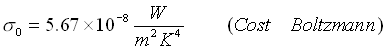
Cerco ![]()
Indico con
![]() Differenza di temperatura tra mattonella e aria
Differenza di temperatura tra mattonella e aria

Si procede per tentativi (soluzione ingegneristica); cioè si attribuisce un valore all’incognita, nel nostro caso la temperatura della mattonella, e, con l’aiuto delle tabelle e delle equazioni già scritte, si può sapere di quanto la soluzione tentativo si avvicina a quella esatta.
1) I TENTATIVO: ![]()
Dalla definizione del Numero di Grashof 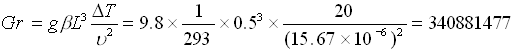
Dalle tabelle, ![]()
Dalla definizione del Numero di Rayleigh, ![]()
Poiché ![]() il regime è turbolento e posso usare la formula di
il regime è turbolento e posso usare la formula di
Fishenden e Saunders:
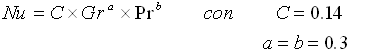
Quindi ![]()
Dalla relazione tra ![]() trovo che
trovo che
![]()
Quindi, risolvendo l’equazione (1), dopo aver sostituito il termine di tentativo nel termine lineare, trovo che:
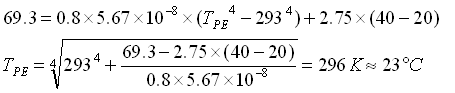
2) II TENTATIVO ![]() Ripetendo le operazioni fatte nel I tentativo:
Ripetendo le operazioni fatte nel I tentativo:
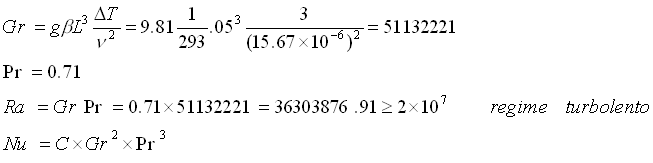
con : C=0.14 a=b=0.3
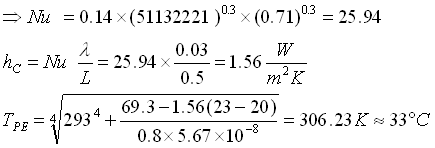
![]() 3) III TENTATIVO
3) III TENTATIVO ![]()
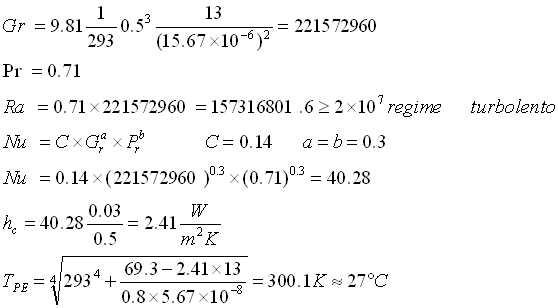
4) IV TENTATIVO ![]()
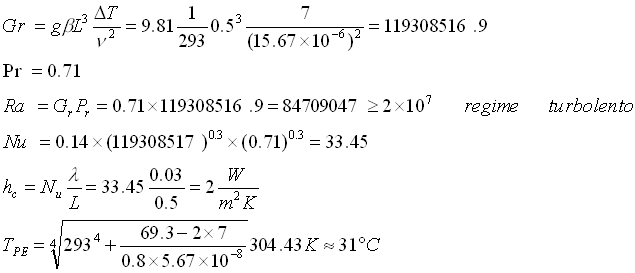
5) V TENTATIVO ![]()
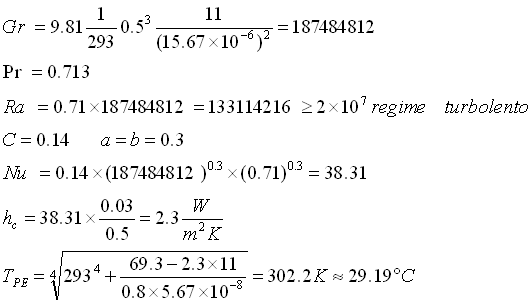
6) V I TENTATIVO ![]()
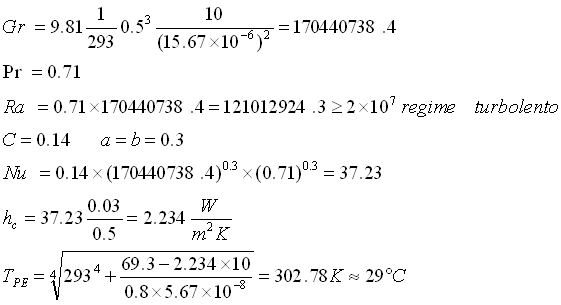
Quindi la temperatura cercata sarà circa 29.5 °C.
Ulteriore domanda
Supponendo 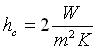
Qual è il coefficiente di irraggiamento hR nei due casi?
Risoluzione
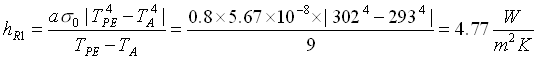
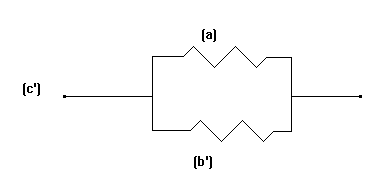
La rete elettrica equivalente è :
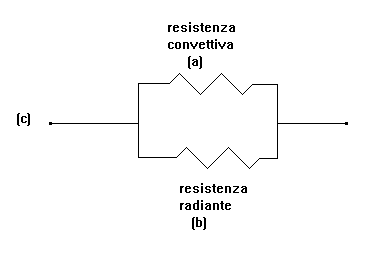
Con
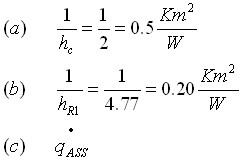
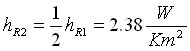
La rete elettrica equivalente è :
Con :
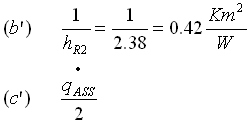
Da questo esempio si osserva che il corpo con a=0.4 si scalda meno di quello con a=0.8. Da ciò si deduce che più è basso il coefficiente di assorbimento, meno un corpo si sbaglia.
Si può costruire per punti un diagramma del sovralzo della temperatura di un corpo in funzione del suo coefficiente di assorbimento.
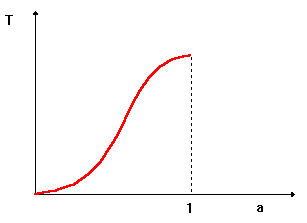
Figura 5 - Grafico del sovralzo di temperatura di un corpo in funzione del suo coefficiente di assorbimento.
Questo risultato è confermato anche dall'esperienza quotidiana; ad esempio in estate , le automobili nere parcheggiate al sole possono raggiungere temperature superiori ai 70°C, mentre quelle bianche esposte al sole per lo stesso periodo di tempo non superano i 40°C.
Questo appunto a causa del diverso coefficiente di assorbimento della carrozzeria delle due automobili.
Un altro esempio può essere quello delle CPU dei computer: una CPU nera funziona senza surriscaldarsi, una CPU di alluminio si surriscalda più facilmente, proprio perché quella nera scambia molto più calore per irraggiamento con l'esterno a causa del suo maggiore coefficiente di assorbimento.