RELAZIONE DI FISICA TECNICA
ONDE STAZIONARIE
GALLINARI DANIELE
INDICE:
TEORIA DELLE ONDE STAZIONARIE
TUBO DI KUNDT
SOLUZIONE DEL PROBLEMA SU BASE ENERGETICA
1. TEORIA DELLE ONDE STAZIONARIE
Le onde stazionarie si hanno ad esempio in un tubo quando invece di essere infinitamente esteso, è chiuso con una terminazione rigida, quindi l’onda picchia e torna indietro (fig 1). Siamo nella situazione in cui all’onda progressiva corrisponde anche un’onda regressiva. Quindi la soluzione generale dell’equazione di Helmholtz è:
![]()
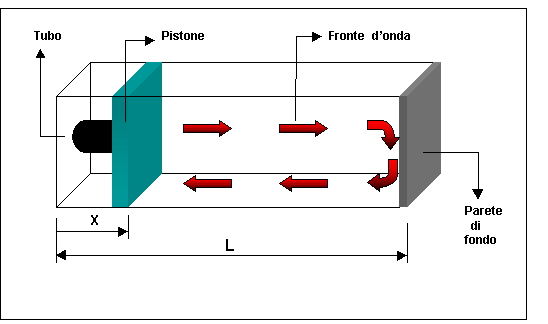
![]() Fig 1- Andamento dell’onda in un tubo a terminazione rigida
Fig 1- Andamento dell’onda in un tubo a terminazione rigida
Vedo un fronte d’onda progressivo che va da sinistra verso destra e uno regressivo da destra a sinistra; si ha un potenziale che ha una parte positiva che va verso le x crescenti (quindi con un segno meno del termine kx).Infatti per ritrovare questo segnale che si aveva ad un certo istante all’istante successivo dovrò incrementare la x perché l’argomento di questa funzione potenziale viene mantenuto costante per x crescenti al variare del tempo. Viceversa sovrapposto ho un fronte che viaggia in senso opposto. La x va decrementata al variare del tempo per mantenere il termine costante.
Il potenziale è legato alla pressione dalla relazione di Eulero ed alla velocità tramite il potenziale:
![]()
dove :
![]()
Con k = numero d'onda
c = velocità del suono
Bisogna applicare le condizioni al contorno opportune per poter risolvere questa equazione, condizioni che sono date da una certa velocità sul vettore mobile ,quindi è più comodo usare l’equazione della velocità:
![]()
Le condizioni che impongo sono considerare un certo valore di velocità sul pistone (per x= 0) ed un valore di velocità nulla per x= L (L= lunghezza del tubo)
Se per x= L la velocità si annulla, vuol dire che in quel punto il valore dell’impedenza è infinito, quindi la terminazione rigida equivale ad una terminazione ad impedenza infinita. Da queste condizioni si ricava algebricamente che i due termini in parentesi devono annullarsi cioè
![]()
Quindi un tubo a terminazione rigida è un tubo in cui il modulo del potenziale non cambia.
Il valore assoluto del potenziale dipende dalla velocità massima che impongo nel punto di eccitazione del sistema ;imponendo U(-L)=(U max) si ottiene:
![]()
Tolgo il valore eiw t perché mi interessa il valore massimo dell’escursione. Posso quindi ricavare il valore del potenziale che rende vera l’equazione.
Nella pratica interessa poco determinare il rapporto tra U ed il potenziale, interessa molto di più vedere cosa succede spazialmente all’interno del tubo. Vado allora a diagrammare P ed U.
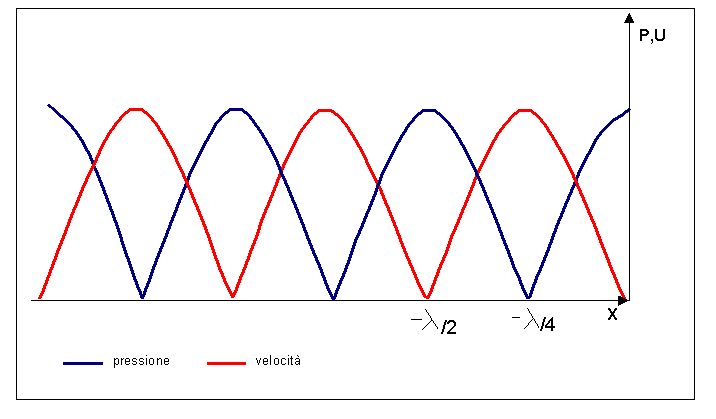
Fig 2 – Diagramma della pressione e della velocità
All’inizio U=0 e P= max. Questo lo vedo dal fatto che nelle formule di P e U i due potenziali hanno segno discorde quindi nella formula della P si sommano mentre in quella di U si sottraggono.
Il primo termine e-ikx ruota in senso orario (al variare di x),il secondo termine e+ikx ruota invece in senso antiorario, come è mostrato dal grafico di fig 3 ;quando kx=1/4 della lunghezza d’onda in realtà la differenza tra e+ikx ed e-ikx è di 180°.
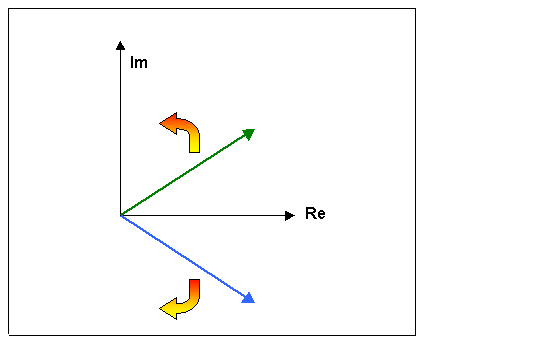
Fig 3 – Andamento dei fasori nel piano complesso
Analizziamo a questo punto l’impedenza:
![]()
Ogni ¼ di lunghezza d’onda la Z varia tra 0 ed infinito. Se facessimo un diagramma di Z si otterrebbero una serie di picchi dove U si annulla (punti ad asintoti verticali).
Quando P si annulla Z si annulla, quando U si annulla Z va ad infinito.
L’eccitazione del sistema è molto delicata infatti se vado a mettere il pistone, che genera il segnale in una situazione di impedenza infinita(considerando il pistone anch’esso rigido),mi trovo in una situazione di velocità praticamente nulla, ho il massimo trasferimento di energia e in teoria sono in una condizione di pressione infinita.
Se invece il pistone viene messo in zona dove U è massima e la pressione nulla ho un trasferimento di energia nullo. Se c’è lo spostamento ma non c’è la forza, non c’è energia.
In tutte le situazioni intermedie avremo un trasferimento di energia intermedia tra 0 ed infinito quindi siamo in una situazione instabile specie ad alte frequenze dove la lunghezza d’onda è piccola: il pistone nel corso della sua corsa può trovarsi in una zona ad impedenza variabile quindi il sistema non è lineare.
Il sistema stesso dipende dall’entità del carico applicato, ed i campi reattivi e stazionari sono altamente instabili dal punto di vista energetico.
L’applicazione pratica di tutto questo non c’è quando la terminazione ha un’impedenza infinita.
Analizziamo il caso di impedenza minore di infinito, attraverso la misura della pressione lungo l’asse del condotto.
Scrivere la formula (7) con il potenziale o con la pressione è la stessa cosa perché esiste un legame di proporzionalità diretta tra il valore della pressione e quello del potenziale. Preferisco usare la pressione perché è più semplice da misurare:
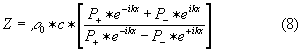
Osservo che il punto dove avrò P massima e la velocità minima non sarà dov’era prima ma spostato e la velocità minima non sarà 0 ma un valore diverso. Analogo ragionamento per P che non sarà massima sulla terminazione. La situazione è meno chiara ,ma ci saranno comunque dei picchi (muovendo il microfono lungo il condotto avrò sempre dei punti dove P è massima e U è minima).
Allora supponiamo di avere fatto la misura. Consideriamo solo il grafico delle P(fig 4).Non importa dove sia la terminazione, considero una zona centrale del condotto.
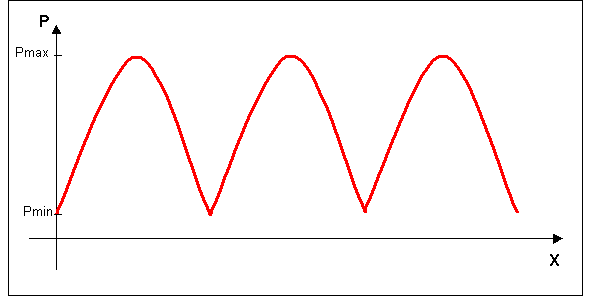
Fig 4 – Andamento della pressione considerando una zona centrale del tubo
La ricerca dei valori di massimo risulta agevole (perché l’andamento del grafico in prossimità dei massimi è dolce).La misura dei minimi è più difficile soprattutto alle alte frequenze quando la lunghezza d’onda è piccola: non riesco ad effettuare questa misura se non tramite l’uso di una vite micrometrica per muovere il microfono. Quest’ultimo è legato ad uno strumento che permette di leggere la pressione: determino la pressione massima e quella minima:
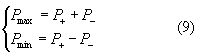
Quando conosco P+ e P- posso determinare l’impedenza.
L’impedenza del materiale sarebbe quella valutata in x=0,cioè sulla terminazione, equazione derivata dalla soluzione ad impedenza infinita:
![]()
![]()
Questa formula in realtà mi da solo il modulo dell’impedenza e sarebbe il risultato corretto solo se l’impedenza fosse reale, ma nella realtà i materiali hanno impedenza complessa: non sarò esattamente sulla parete con il massimo, sarò spostato di una certa x (fig 5).
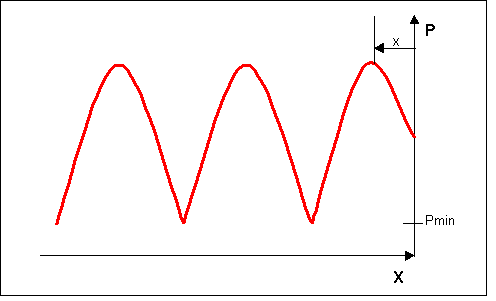
Fig 5 – Andamento reale della pressione (massimo spostato dalla parete)
Il modulo sarà determinato guardando come varia il modulo lungo l’asse del condotto, ma se voglio la fase non posso usare solo i valori massimi e minimi della pressione devo sapere anche la distanza del massimo dalla terminazione. Sapendo che il vettore ruota di 2kx ottengo che l’impedenza sarà:
![]()
Dal punto di vista operativo l’impedenza non serve a molto. Di solito quando un’onda picchia su una parete quello che interessa è il coefficiente di assorbimento acustico a ,che non è una grandezza complessa ma un parametro puramente energetico. Per determinarlo si consideri l’intensità dell’onda stessa, la quale quando picchia contro una parete (intensità incidente II ) viene divisa in due parti: intensità assorbita(IA ) ed intensità riflessa (IR ) (fig 6)
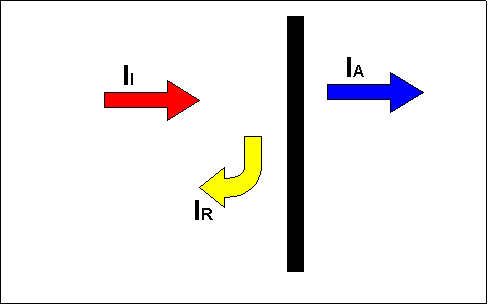
Fig 6 – Andamento dell’intensità dell’onda in prossimità della parete
![]()
![]()
![]()
Dove r è il coefficiente di riflessione.
Si può quindi vedere a come:
![]()
Le intensità per le onde progressive sono calcolate dal quadrato della pressione:
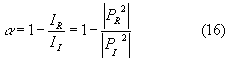
Il coefficiente di assorbimento è una grandezza chiara e ben definita, rappresenta il rapporto tra l’energia dell’onda riflessa e l’energia dell’onda progressiva, interessano i moduli di P, non si tiene quindi conto della fase.
Ora dalla (10) ricordo che Z è il rapporto tra la somma delle onde riflesse ed incidenti e la loro differenza. Posso anche esprimerla come:
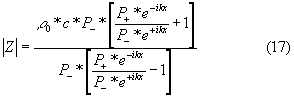
Definisco ora il rapporto di riflessione complessa
![]()
Dalla (17) e dalla (18) ottengo:
![]()
Mi interessa il modulo di R perché il rapporto di riflessione complessa è la radice quadrata del coefficiente di riflessione.
Posso calcolare a :
![]()
Il modulo dell’impedenza serve per calcolare il coefficiente di assorbimento. Se vado a sostituire l’espressione che ottengo nella (9) .Se indico con n il rapporto tra la Pmax e la Pmin, posso riscrivere la formula (19) in funzione del rapporto n:
![]()
Dalla (21) posso scrivere la (20) come:
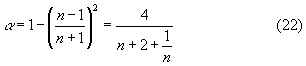
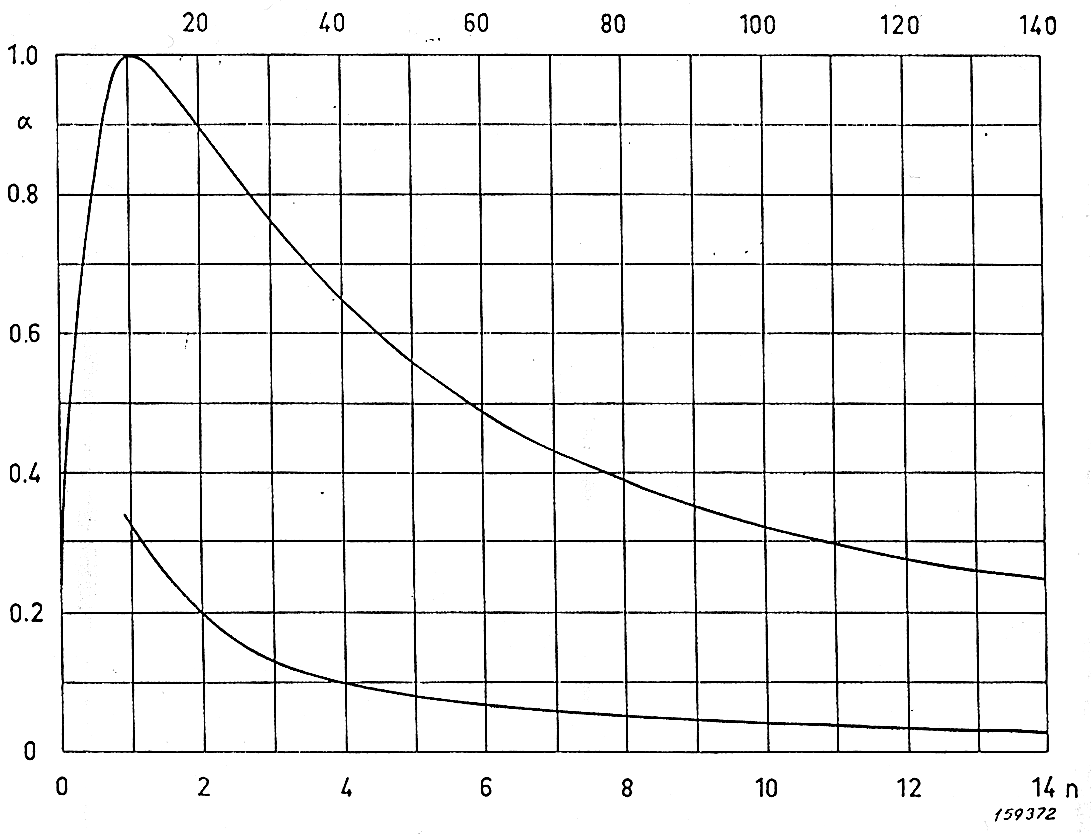
Fig 7 – Andamento del coefficiente di assorbimento in funzione di n
Posso misurare il coefficiente di assorbimento di un materiale posto in fondo ad un tubo andando a trovare Pmax e Pmin. Ottengo a .Questo se non mi interessa l’impedenza in modulo e fase. Se mi interessa posso ricavare Z.
Dalla (19) e dalla (21) ricavo l’impedenza:
![]()
Devo conoscere la posizione del massimo di velocità e del minimo della pressione, quella che definisco xmin (fig 7): infatti devo mettermi in un punto dove i vettori sono in fase e Z è reale e minima. Questo accade dove U è massima e P+ e P- sono sfasati di 180°(cioè la P è minima),ad una distanza xmin dalla terminazione. Il minimo è più facile da determinare perché xmin è un punto più preciso di xmax Il valore della Pmax è più facile da determinare ma è più difficile misurare la posizione. Poiché la fase cambia facilmente allo spostarsi di pochi mm sul grafico si preferisce usare xmin. Inoltre è indipendente dal numero di giri.
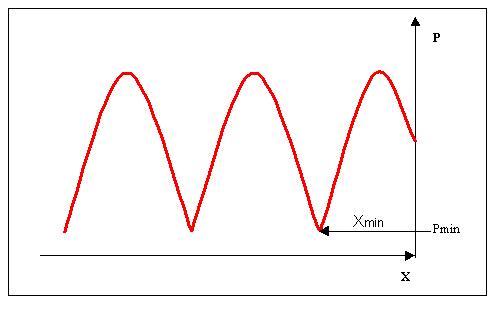
Fig 8 – Posizione in cui Z è reale e minima alla distanza Xmin
Il vettore fa un giro completo ogni mezza lunghezza d’onda, quindi non importa quale minimo sto misurando. L’importante è misurare un minimo e la distanza di questo dalla parete stessa. La fase in questi punti è sempre uguale; fatto un numero intero di mezzi giri torna sempre nello stesso punto.
2. TUBO DI KUNDT
Analizziamo a questo punto la strumentazione normalmente utilizzata per la misura del coefficiente di assorbimento a ,strumentazione che consiste nel cosidetto tubo di Kundt o tubo ad onde stazionarie(fig 8).
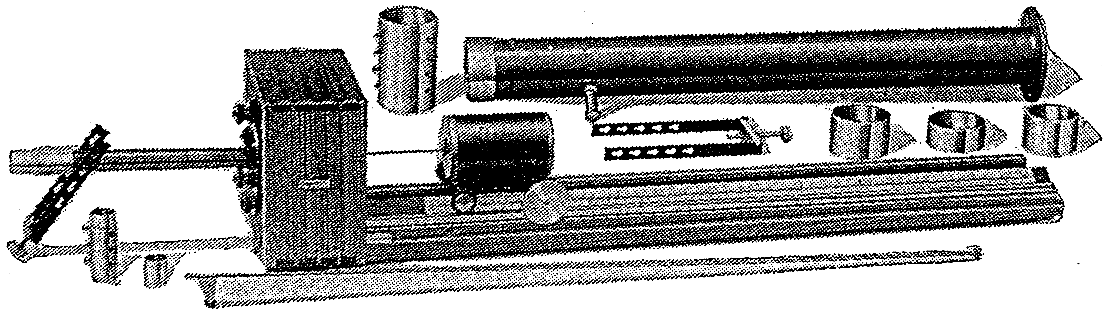
Fig 9 – Tubo di Kundt
Questo strumento è costituito da una cassetta all’interno della quale è montato un altoparlante. Sulla cassetta viene a sua volta montato un tubo di 29 mm per le misure ad alte frequenze e di 99 mm per le misure di frequenze basse ( intorno ai 1800 Hz ). Sulla terminazione monto dei tappi d’acciaio all’interno dei quali colloco il provino. I tappi vengono montati su un bicchiere che a sua volta viene fissato sul tubo tramite una staffa con un tirante per tenere pressato il provino contro il tubo. All’interno dell’altoparlante scorre un tubicino che porta il microfono che corre su un carrellino ; sulle ruote del carrellino c’è una scala graduata, il tubicino scorre avanti e indietro con il microfono che è collegato ad un voltmetro che misura un valore RMS della forma d’onda; trovo il massimo ed il minimo e prendo nota del valore. Non importa di calibrare il microfono, quindi se misuro in Volt o Pascal, perché tanto interessa il rapporto. Uso un frequenzimetro, e ripeto la prova per ogni frequenza.
E’ importante conoscere lo spessore del provino per posizionare correttamente lo zero sulla scala graduata, per questo uso un supporto variabile che consente di posizionare micrometricamente la superficie del provino in modo che coincida con lo zero della scala graduata come in fig 9 Se si vuole l’impedenza assoluta in modulo ed in fase la distanza della superficie del provino è molto importante.
Il segnale arriva al microfono tramite un sondino ( indicato con il numero 332).
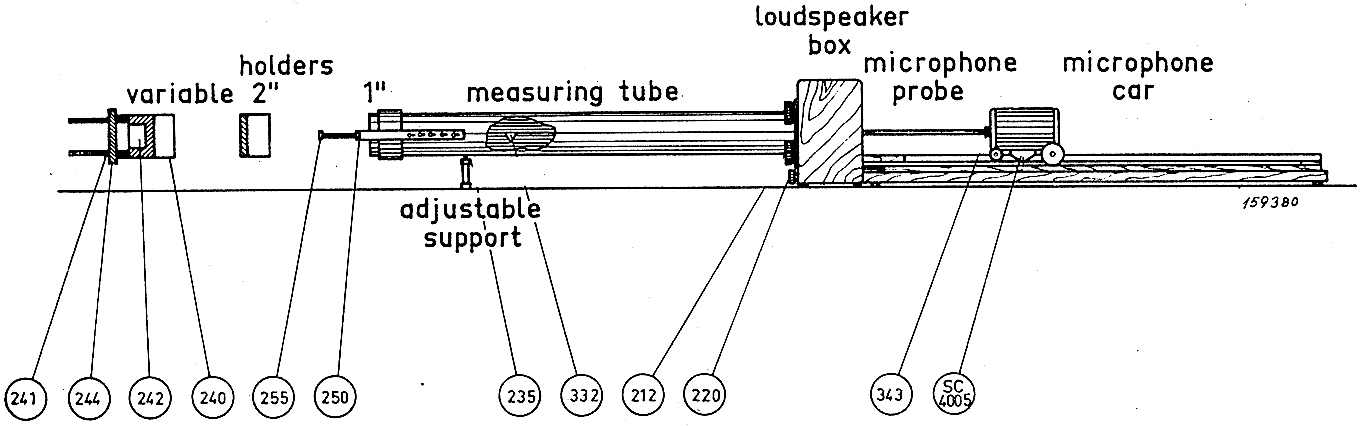
Fig 10 – Schema del Tubo di Kundt con supporto variabile
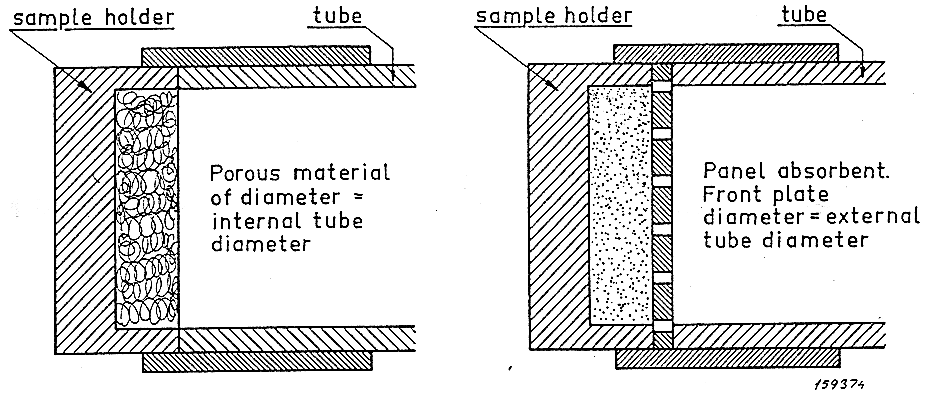
Fig 11 – Particolare del bicchiere e del provino
Il sistema è collegato ad una strumentazione analogica: collegato al microfono c’è un voltmetro a lancetta, mentre per generare le frequenze uso un generatore sinusoidale a valvole
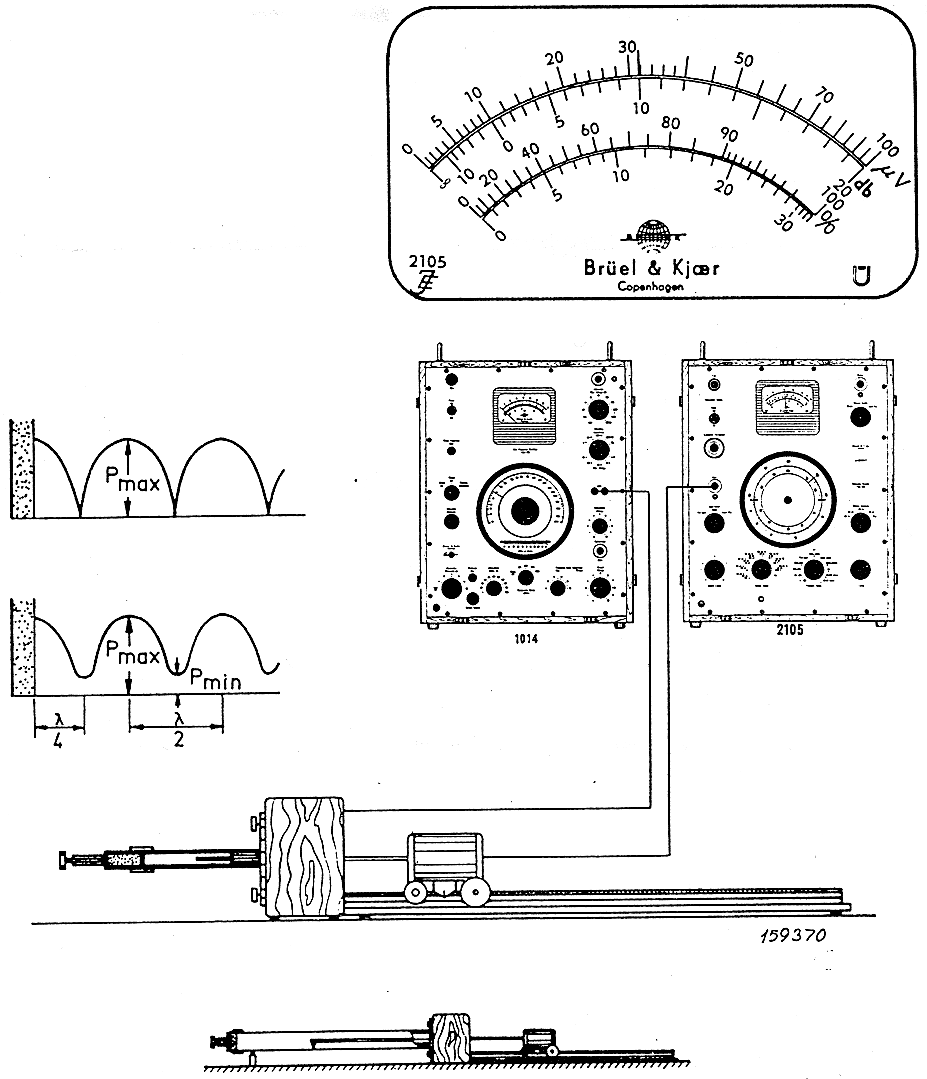
Fig 12 – Strumentazione analogica per rilevazione dati.
3. SOLUZIONE DEL PROBLEMA SU BASE ENERGETICA
La soluzione più semplice è su base energetica, si basa sulla misura della densità e intensità sonora.
Mi metto dentro il tubo che ha la terminazione di un certo materiale con un certo a incognito. Genero un treno di onde progressive che chiamo II. Poiché la terminazione non è completamente assorbente si avrà un treno che di onde riflesse che viaggia in senso opposto con intensità IR come visto in figura 6.
Il mio strumento di misura non è però in grado di misurare separatamente II da IR.
Se prendo una sonda intensimetrica speciale (cioè a doppio microfono) che misura tutto (U,P,I) e la metto dentro il tubo questa non mi misura II ed IR ma ITOT definita come:
![]()
Prendo un verso positivo dell’intensità verso destra ed il valore sarà positivo perché II è maggiore di IR perché la parete non può ributtarmi maggiore intensità di quella che gli mando.
Per calcolare a mi interessano II ed IR ma separatamente.
Ne posso comunque misurare la somma, o meglio posso misurare la densità totale di energia che gode della proprietà additiva :
![]()
Entrambe vengono misurate e non dipendono dal punto di misura. Mentre P ed U creano problemi I e D sono costanti ovunque quindi non mi interessa muovermi cercando un punto particolare. Posso mettere la sonda più lontano o più vicino ed in ogni misurare la stessa I e D.
Altro vantaggio: non ho fatto alcuna ipotesi di tono puro, quindi non ho bisogno di quelle equazioni scritte alla Helmholtz con w esplicitata dove posso i conti solo una frequenza alla volta. La misura può essere effettuata simultaneamente su tutte le frequenze senza muovere il microfono.
Il problema fondamentale è ricavare II ed IR conoscendo la somma e la differenza .
Ricavo IR dalla (25):
![]()
Sostituendo nella (24) ricavo:
![]()
Risostituendo nella (26) ottengo:
![]()
A questo punto dalla (16) ricavo il coefficiente di assorbimento acustico:
![]()
Posso anche esprimere questo fatto in un altro modo: definisco velocità dell’energia acustica come:
![]()
Quindi si tratta di un vettore allineato con il vettore velocità. Il suo valore va da zero (non c’è propagazione di energia) alla velocità del suono (il campo è tutto attivo). Posso quindi determinare quando il campo è reattivo: introduco b , coefficiente di propagazione, che va da 0 (caso di onda stazionaria, quindi non c’è propagazione quindi il campo è completamente reattivo) ad 1 (caso di onda piana e progressiva senza onda riflessa, quindi nel caso di completo assorbimento del materiale):
![]()
Ottengo:
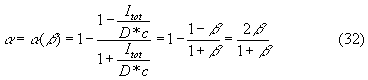
b
è un parametro che lo strumento mi da subito perché è dato dal rapporto tra l’intensità e la densità sonore, normalizzato alla velocità del suono, quindi si tratta di un numero puro che si misura direttamente in qualunque campo acustico, il tutto con due enormi vantaggi:- non devo lavorare ad una frequenza alla volta
Il problema principale in questo procedimento consiste nel fatto che non esistono ancora norme ISO che regolano questo nuovo metodo e la misura dell’intensità acustica non risulta facile.