sono le perdite di carico dovute ad irregolarità geometriche dei tubi nei quali scorre il fluido (come ad esempio un brusco restringimento od allargamento di sezione, un gomito, una giunzione a "T", ecc.). Questa classe di perdite di carico sono anche dette LOCALIZZATE, poiché sono generate in un luogo ben preciso del tubo.

Per calcolarle esistono due metodi distinti:

Metodo 1: definendo un coefficiente adimensionale b tale che moltiplicato per la velocità media W al quadrato e diviso per due mi dà il valore della perdita di carico concentrata R_C:

(1)

b viene definito COEFFICIENTE DI PERDITA CONCENTRATA ed è funzione del fattore di forma geometrico (cioè della forma e dimensione geometrica del tubo) e del numero di Reynolds:

Tuttavia nella pratica si approssimano i valori di b costanti in funzione del tipo di accidentalità che si presenta nel circuito idraulico. I valori di b sono tabellati:

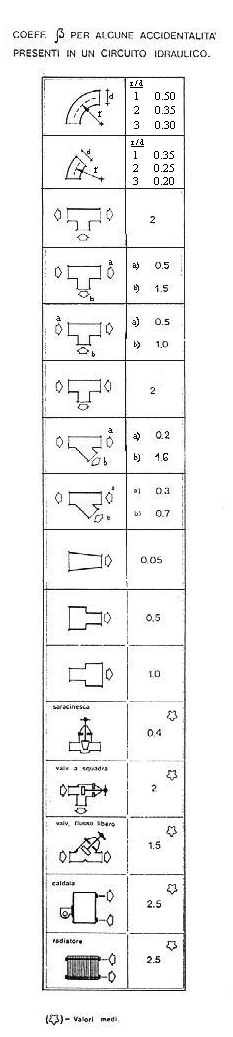
Tabella 1

Un esempio dell’utilizzo della tabella 1 è il seguente:

dato un condotto che presenta un "gomito a 180° ", per ottenere il b complessivo occorre sommare per due volte i b dell’accidentalità "gomito a 90° ". Numericamente abbiamo che b "gomito a 90° " (con fattore di forma geometrico r/d pari a 1) è 0,5, quindi per il "gomito a 180° " risulta 0,5+0,5 = 1.

Se in un circuito idraulico sono presenti diversi tipi di accidentalità, la perdita di carico concentrata totale R_Ctot è pari alla somma della perdite di carico dovute alle singole accidentalità:

(3)

ove b _i è caratteristica di ogni singola accidentalità.

Analogamente la perdita di carico distribuita totale R_Dtot di un certo circuito idraulico complesso (cioè composto di tubi di diversi diametri) la si ottiene sommando le singole perdite di carico distribuite:

(4)

ove x_i sono i fattori d’attrito per ogni tratto di tubo.

Infine la perdita di carico totale (distribuita più concentrata) di un qualunque circuito idraulico è data da:

(5)

Metodo 2: Il secondo metodo per esprimere le perdite di carico concentrate consiste nell’accorpamento delle perdite di carico concentrate con le perdite di carico distribuite ottenuto allungando fittiziamente il tubo; cioè si incrementa il valore della lunghezza del circuito idraulico (e quindi delle perdite di carico distribuite) di un valore (definito LUNGHEZZA EQUIVALENTE L_eq) che è desumibile dal nomogramma in Fig.1.

Il nomogramma si utilizza seguendo le seguenti regole:

• Individuo nella dicitura in basso il numero indicativo del tipo di accidentalità.
• Traccio una retta fra i seguenti due punti:

1. Il punto posto sulla I riga verticale all’altezza del numero indicativo dell’accidentalità.
2. Il punto posto sulla III riga verticale in corrispondenza del valore del diametro del tubo.

• L’intersezione della retta tracciata con la II riga verticale è il punto che mi indica il valore della lunghezza equivalente.

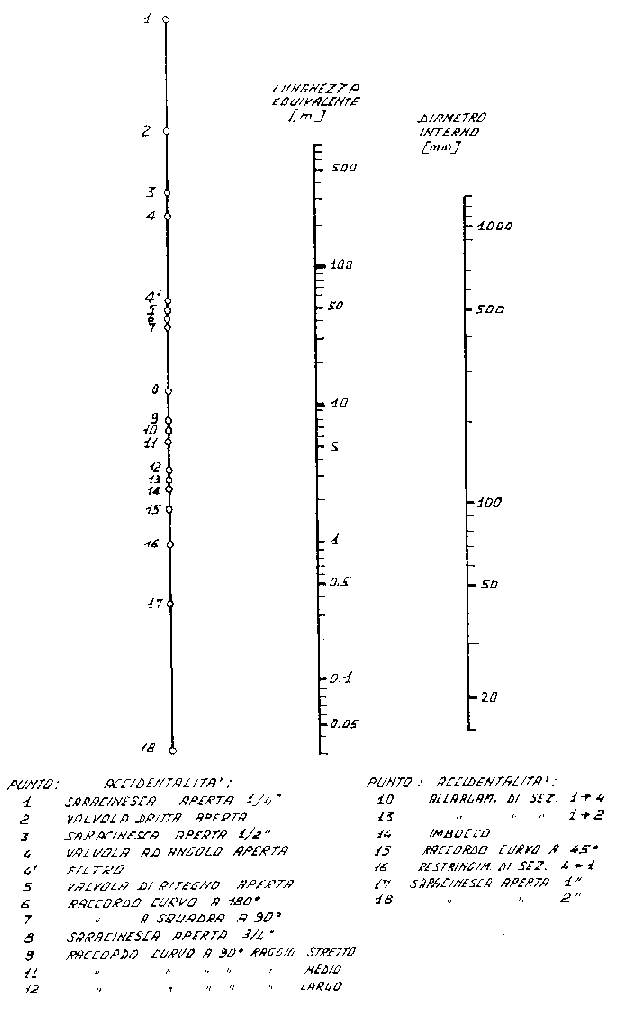
Fig. 1 – Nomogramma della lunghezza equivalente

Es. 1) Suppongo di avere un’accidentalità del tipo raccordo a squadra a 90° (numero indicativo 7) e di avere un tubo di diametro 100 mm, allora dall’utilizzo del nomogramma:

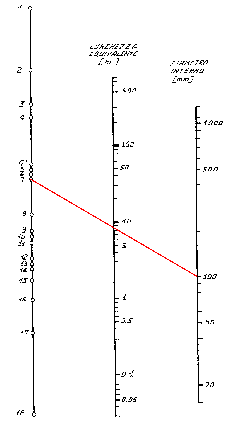
Fig. 2 – Applicazione del nomogramma nella risoluzione dell’esempio 1

ricavo che la lunghezza equivalente è pari a 7,5 m cioè al punto d’incrocio della retta (rossa in Fig.2 ) con la II riga verticale.

Es. 2) Suppongo di avere come accidentalità un brusco imbocco (numero indicativo 14) in un tubo di diametro 500 mm, utilizzando il nomogramma:

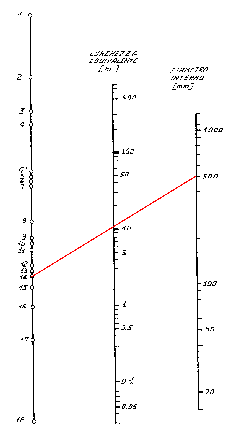
Fig. 3 – Applicazione del nomogramma nella risoluzione dell’esempio 2

ricavo che la lunghezza equivalente è circa 10 m.

Con questo secondo modo di esprimere le perdite di carico distribuite, la formula della perdita di carico totale (distribuita più concentrata) assume la seguente forma:

(6)

ove la lunghezza equivalente L_eq, nel caso di più accidentalità, è definita come la somma delle singole lunghezze equivalenti di ogni accidentalità:

(7)

E’ importante ricordare che i due metodi sopra descritti per esprimere le perdite di carico concentrate sono metodi distinti, cioè l’utilizzo di un metodo esclude l’utilizzo dell’altro.

Risulta evidente, viste le approssimazioni fatte, che la precisione nel calcolo delle perdite di carico è molto bassa, per questo motivo il margine d’errore tollerabile nei problemi di dimensionamento idraulico è del 50% sia in eccesso che in difetto. Questo significa che se per esempio si deve dimensionare una pompa per un circuito idraulico e dallo studio analitico sopra descritto, troviamo che la pompa deve avere una pressione di 10 bar, è sensato visti i margini d’errore, decidere d’acquistarne una da 15 bar così da essere sicuri che anche nel caso peggiore (errore pari a –50%) nel circuito idraulico l’acqua girerà alla velocità desiderata. E se l’errore è in difetto (errore pari a +50%) sarà sufficiente collegare il motore elettrico della pompa in modo da girare a velocità ridotta per diminuire la pressione della pompa.

Vogliamo ora calcolare le perdite di carico nel caso di tubi a sezione non circolare.

Per far ciò sarà sufficiente sostituire nella formula delle perdite di carico in tubi a sezione circolare un diverso fattore d’attrito x. Nel calcolo di x possiamo suddividere l’analisi in due casi:

1. Nel caso di moto laminare in tubi circolari sappiamo che

(8)

ove x è il valore costante 64. Nei tubi non circolari è sufficiente sostituire alla x il valore desumibile dalla colonna "laminare" della tabella seguente:



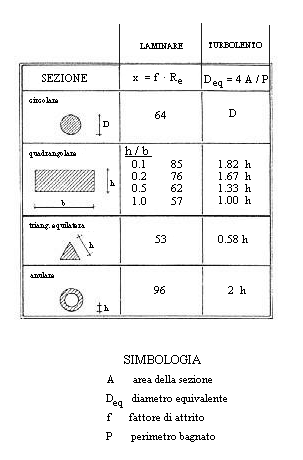
Tabella 2

 

2. Nel caso di moto turbolento il procedimento è il seguente:

• Si calcola il DIAMETRO EQUIVALENTE D_eq che è definito dalla seguente relazione:

(9)

ove P_b è la parte del perimetro del condotto bagnato dal fluido e A è l’area della sezione.

Valori del diametro equivalente per i tipi di sezione più comuni sono desumibili dalla colonna "turbolento" della tabella 2 riportata sopra.

• Si calcola il numero di Reynolds R_e e la scabrezza relativa utilizzando le seguenti formule:

(10)

(11)

• Infine si utilizza il diagramma di Moody (esattamente come nel caso del tubo a sezione circolare, ma utilizzando i valori della scabrezza relativa e del numero di Reynolds calcolati al punto precedente) per ottenere il fattore d’attrito x.

Abbiamo visti due tipi di strumenti:

1. MANOMETRO DIFFERENZIALE:

Questo apparecchio misura direttamente la variazione di pressione fra due punti (P1 e P2 in fig.4). Un modello di questo trasduttore, che abbiamo già analizzato nella lezione precedente, è formato da una vasca di liquido dalla quale esce un tubo, ed il livello del liquido in tale tubo è proporzionale alla variazione di pressione. Il tipo di misuratore appena descritto è stato sostituito da strumenti tecnologicamente più avanzati che sfruttano la caratteristica degli strain gate. Lo strain gate è una resistenza elettrica il cui valore è proporzionale alla forza di contrazione o di trazione applicata ai capi della resistenza elettrica.

 

 



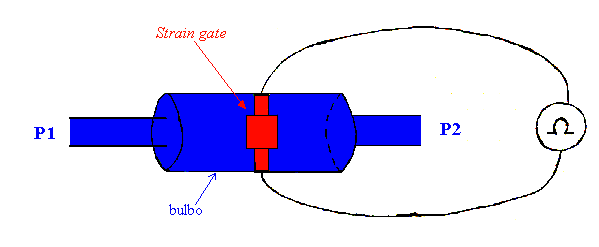
Fig. 4 – Applicazione dello strain gate come misuratore di pressione

 

 

 

Riferendomi allo strumento in fig.4 posso osservare che se la differenza di pressione D P=P2-P1 è diversa da zero allora vi è un’espansione del bulbo e quindi lo strain gate sarà sottoposto a una forza di trazione proporzionale alla pressione D P. Dalla misura della resistenza elettrica si determina la variazione di pressione D P che è presente fra i due condotti.

 

 

 

 

2. MANOMETRO A VALORE ASSOLUTO:

Strumento che misura il valore assoluto della pressione P per mezzo dell’utilizzo di un cristallo piezoelettrico il quale ha la caratteristica di variare la differenza di potenziale ai suoi capi al variare della pressione alla quale è sottoposto. Un esempio di manometro a valore assoluto è il manometro a vite riportato in fig.5.

Il cristallo piezoelettrico è posto fra un supporto fisso e un piccolo foro sul quale agisce la pressione del fluido che tende a comprimere il cristallo piezoelettrico al quale è collegato un Voltmetro che misura così la differenza di potenziale ai capi del cristallo e da questa misura posso determinare il valore della pressione P del fluido.

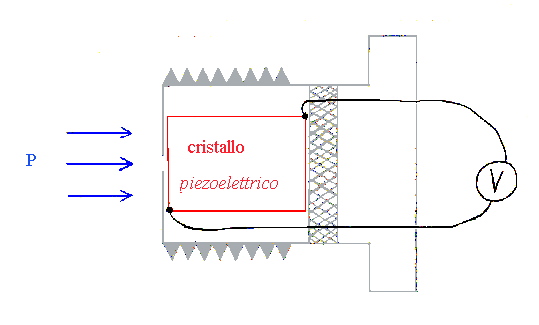
Fig. 5 – Manometro a vite che utilizza il cristallo piezoelettrico

In conclusione se ciò che si vuol determinare è una differenza di pressione D P è conveniente utilizzare un manometro differenziale rispetto ad uno a valore assoluto poiché col primo si commette un errore nella misura minore rispetto all’utilizzo del secondo.

Ricordiamo prima di iniziare la trattazione degli strumenti di misura di portata una relazione che verrà più volte richiamata:

Grazie a questa formula si può ricondurre il problema della misura di portata al più semplice problema della misura della velocità W del fluido nel condotto.

1. I primi strumenti di misura di portata che analizziamo sono il diaframma (Fig. 6a) ed il boccaglio (Fig. 6b) riportati in figura:

 



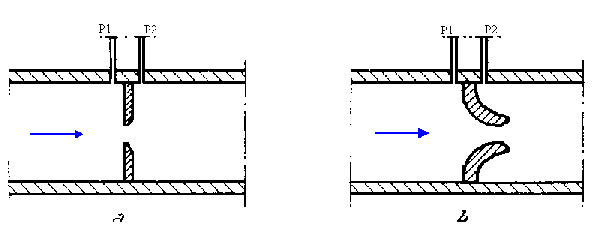
Fig. 6 – Diaframma e Boccaglio

 

Entrambi gli strumenti in figura sfruttano la perdita di carico concentrata ottenuta per mezzo di un restringimento e successivo allargamento della sezione del tubo. Applicando la forma operativa dell’equazione di Bernoulli a questo semplice sistema risulta:

(13)

ove è possibile ottenere la misura di D P per mezzo di un manometro differenziale o delle misure di P₁ e di P₂ per mezzo di un manometro "assoluto". Rielaborando l’equazione di Bernoulli si ottiene

(14)

ove r è la densità del fluido e b , coefficiente di perdita concentrata, è caratteristico dello strumento.

Questo tipo di misuratori di portata presenta il vantaggio di essere facilmente intercambiabile e con un range di velocità W (e quindi di portate dalla 12) misurabili più ampio (grazie a diversi valori di b che può assumere lo strumento) rispetto al tubi di Venturi.

2. I misuratori di portata del I° punto presentano il grande svantaggio di interferire col moto del fluido nel condotto; questa condizione, ad esempio nel caso di applicazioni nell’industria alimentare, causa l’accumulo di residui alimentari, sporcizia nel condotto. Dall’esigenza di avere misuratori di portata che non interferiscono con il flusso sono stati creati trasduttori che vengono montati "a cavallo" del condotto e che sfruttano diversi effetti fisici e diverse proprietà del fluido.

 



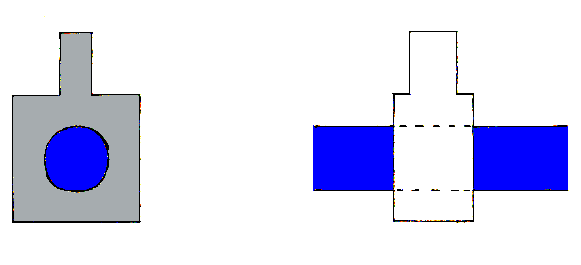
Fig. 7 – Viste dei misuratori di portata esterni al condotto

 

II a) TRASDUTTORE DI TIPO MAGNETICO

Si avvolgono delle spire attorno al condotto e le vi si fa scorrere una corrente variabile nel tempo in maniera tale che nel condotto vi sia un campo magnetico oscillante. Questo campo magnetico viene perturbato (cioè si genera una forza elettromagnetica) dal passaggio di fluido paramagnetico nel condotto (come ad esempio l’acqua). Da misure dell’intensità della perturbazione è possibile risalire alla velocità e quindi alla portata del fluido (per la 12). Risulta evidente dalla descrizione il limite del funzionamento di questo trasduttore: esso funziona solamente in presenza di fluido paramagnetico.

 

II b) TRASDUTTORE AD ULTRASUONI

 



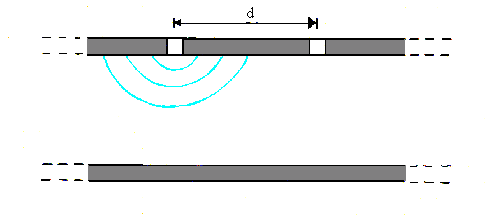
Fig. 8 – Sezione del tubo in cui è posto il trasduttore ad ultrasuoni.

 

Questo traduttore si realizza facendo due minuscoli fori nel condotto ed iniettando un’onda sonora a una frequenza n _o nel primo foro. Misurando la frequenza n _D del suono dal secondo foro per mezzo di un microfono si riesce a risalire alla velocità W del fluido ed alla sua direzione sfruttando l’effetto Doppler. Infatti l’onda sonora iniettata nel primo foro si propaga nel fluido che se è fermo non ne influenza la propagazione (quindi si avrà n _D uguale a n _o); se invece il fluido si sta’ muovendo si misurerà al secondo foro una variazione della frequenza del suono che è direttamente proporzionale alla velocità W del fluido. Dal confronto fra n _o e n _D si ha che se n _D > n _o allora il fluido si stà muovendo con lo stesso verso di propagazione del suono, mentre se n _D < n _o allora il verso di propagazione è contrario a quello del suono. Per comprendere meglio questo concetto è bene illustrare un esempio chiarificatore: consideriamo un treno che fischia, se esso si stà avvicinando a noi si sente il suono salire in frequenza (fischio più acuto) mentre se esso si stà allontanando il suono diminuisce in frequenza; inoltre la variazione di frequenza è tanto maggiore quanto maggiore è la velocità del treno.

Un importante vantaggio del trasduttore ad ultrasuoni è quello di poter analizzare la composizione del fluido: iniettando un suono di brevissima durata (impulso) misuro il tempo che quest’ultimo impiega ad arrivare al microfono; ho così la velocità v di propagazione del suono nel liquido:

(15)

Essendo v funzione della composizione del fluido è possibile ottenere la composizione stessa.

 

Questo strumento non consente un’alta precisione nella misura della velocità W del fluido e quindi della portata; ciò implica che il suo utilizzo è sconsigliato in processi nei quali è fondamentale il preciso controllo del tempo di percorrenza del fluido nel tubo (quale ad esempio la pastorizzazione UHT, nella quale è fondamentale che il latte venga riscaldato ad un’alta temperatura per un tempo preciso altrimenti si ha la "cottura" del latte stesso).

 

II c) TRASDUTTORE AD EFFETTO CORIOLIE

 



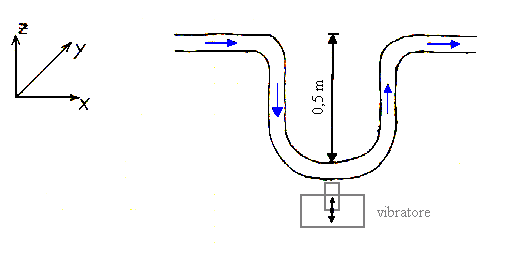
Fig. 9 – Trasduttore ad effetto Coriolie

 

Il misuratore di portata ad effetto Coriolie si realizza aggiungendo al condotto un percorso "a ferro di cavallo" sul piano xy ed al vertice dello stesso viene posto un vibratore che ha il compito di fare oscillare il condotto lungo l’asse z mentre è attraversato dal fluido.

Per rispettare la conservazione della quantità di moto si ha una coppia di forze costante che torce il condotto; questa coppia di forze è dovuta all’effetto Coriolie.

Da equazioni fisiche sappiamo che la velocità W del fluido è proporzionale alla coppia di torsione la quale è facilmente misurabile per mezzo di strain gate posizionati sulle braccia del condotto come in figura.

 

 



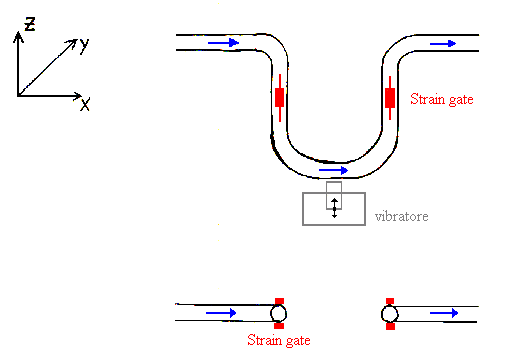
Fig. 10 – Apparato di misura dell’effetto Coriolie per mezzo di Strain gate.

 

Gli svantaggi di questo trasduttore sono legati all’effetto Coriolie: misura unicamente la portata in massa del fluido indipendentemente dal tipo di fluido presente nel condotto ed inoltre è inutilizzabile all’equatore ove l’effetto Coriolie è nullo.

 

II d)ANEMOMETRO LASER – DOPPLER

 



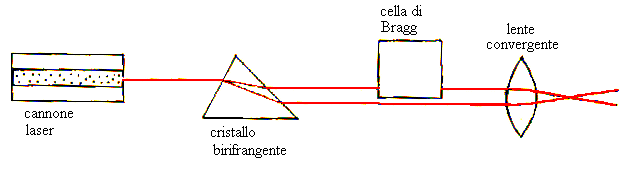
Fig. 11 – Rappresentazione schematica dell’anemometro laser-doppler.

 

Un fascio di luce laser (quindi coerente cioè tutti i fotoni mantengono una differenza di fase costante fra loro) viene sdoppiato da un cristallo birifrangente (cioè con due indici di rifrazione) ed uno dei due fasci formatisi subisce uno shift in frequenza (cioè viene portato ad una frequenza pari a 40 MHz) passando nella Cella di Bragg; infine i due raggi così elaborati passano in una lente convergente e si intersecano nel punto, interno al condotto, in cui voglio misurare la velocità W del fluido. Nel punto di intersezione si hanno fenomeni di interferenza che generano frange chiare e frange scure (cioè luoghi distinti in cui vi è luce e in cui vi è buio che si alternano fra loro); avendo inoltre i due raggi diversa frequenza si potrà osservare un costante movimento delle frange in un determinato verso.

 

 



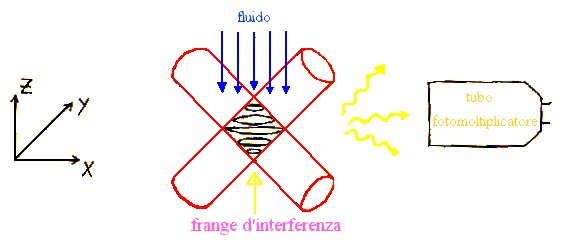
Fig. 12 – Zoom nel punto di intersezione dei raggi laser

 

Il fluido passa in direzione normale al piano delle frange. Se il fluido è trasparente e contenente delle particelle o polveri fotoluminescenti (capaci cioè di emettere luce quando illuminate) quando queste passano nella frangia chiara riflettono la luce, generando così un impulso luminoso, mentre quando attraversano la frangia scura non danno luogo a riflessione; misurando per mezzo di un tubo fotomoltiplicatore (che è un trasduttore fotonico-elettrico) il tempo D t fra due distinti impulsi luminosi emessi dalla particella fotoluminescente si ottiene la frequenza n di emissione con la semplice regola:

(16)

Per meglio comprendere il funzionamento dell’anemometro laser-doppler, studiamo lo strumento senza Cella di Bragg e quindi con le frange fisse nel punto d’intersezione dei raggi laser. Se il fluido nel condotto è fermo, le particelle fotoluminescenti non attraversano le frange chiare e quindi non si ha emissione di impulsi luminosi. Se il fluido è in movimento le particelle fotoluminescenti che attraversano il punto d’intersezione (e quindi la sequenza di frange chiare e scure) emettono una sequenza di impulsi luminosi. Minore è il tempo D t fra l’emissione di due impulsi consecutivi, maggiore è la velocità della particella fotoluminescente.



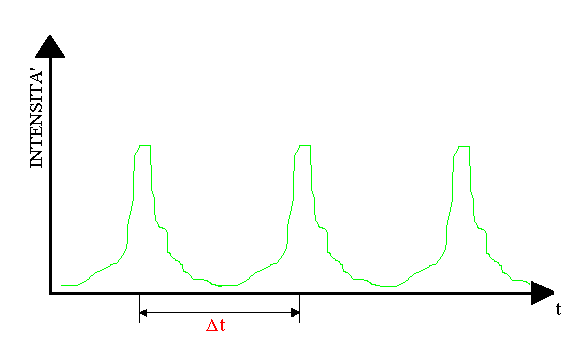
Fig. 13 – Emissioni luminose rilevate dal tubo fotomoltiplicatore nel caso di anemometro laser sprovvisto della Cella di Bragg.

 

Senza l’effetto della Cella di Bragg non si riesce però a determinare il verso del movimento del fluido nel condotto. Analizziamo ora l’anemometro laser-doppler completo: se il fluido è fermo, la frequenza n di emissione della luce da parte delle particelle è 40 MHz cioè la frequenza di movimento delle frange stesse imposta da noi mediante l’inserimento della Cella di Bragg nello schema dell’anemometro.

Se il fluido è in movimento si ha l’effetto Doppler dovuto al contemporaneo movimento sia del fluido che delle frange: se la frequenza n di emissione degli impulsi luminosi dovuti alle particelle è maggiore di 40 MHz significa che la particella fotluminescente e quindi con essa il fluido si stà muovendo in senso opposto rispetto al verso di scorrimento della frange. Dalla misura di n si riesce a risalire alla velocità W del fluido poiché, come nel caso del trasduttore ad ultrasuoni,

essa è proporzionale alla frequenza n .

 



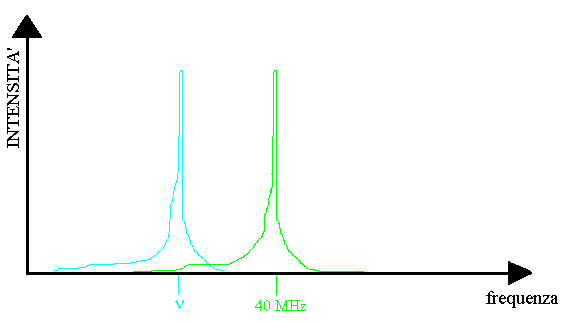
Fig. 14 – Grafico della variazione della frequenza di emissione degli impulsi luminosi con il fluido in moto

 

Questo dispositivo presenta lo svantaggio di essere molto costoso e funziona solo con liquidi trasparenti, nei quali è possibile mischiare particelle fotoluminescenti, e che possono essere contenuti in condotti anch’essi trasparenti ai raggi laser. Nonostante questi svantaggi è uno strumento di altissima precisione nella misura della velocità, che riesce ad analizzare un’area ristrettissima (praticamente puntiforme) del condotto poiché la misura viene effettuata nel punto d’intersezione dei raggi laser.

 

3. RUOTAMETRO

Questo strumento, come il precedente richiede un condotto trasparente, ma il suo funzionamento è al quanto più semplice: il fluido entra nel verso della freccia di Fig.15 ed esercita un forza di tipo tangenziale sul "galleggiante" che comincia a salire. Il condotto nel quale è contenuto il "galleggiante" presenta una sezione maggiore man mano che il "galleggiante" sale, in modo tale da diminuire le forze tangenziali che agiscono su di esso che così tende a stabilizzarsi ad un certo livello. Se il ruotametro è stato opportunamente tarato il valore raggiunto sulla scala graduata dal "galleggiante" è la portata.

 



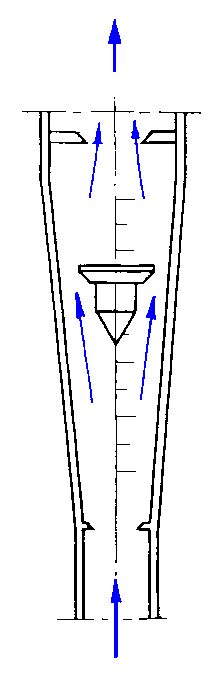
Fig. 15 – Figura del Ruotametro

 

4. ANEMOMETRI A PRESSIONE

Possono essere di due tipi:

1. RUOTA A PALETTE: È composto da un albero su cui è montata la ruota che sostiene le palette (vedi Fig.16). Se le palette sono immerse in un fluido in movimento, si genererà una coppia di forze dovuta alla diversa forma aereodinamica delle stesse, che avrà come effetto quello di far girare la ruota con le palette. Maggiore è la velocità del fluido, maggiore è la coppia di forze, maggiore è la velocità di rotazione delle palette; quindi dalla misura di quest’ultima si risale alla velocità del fluido. Questo genere di anemometro a pressione è molto utilizzato in meteorologia.

 



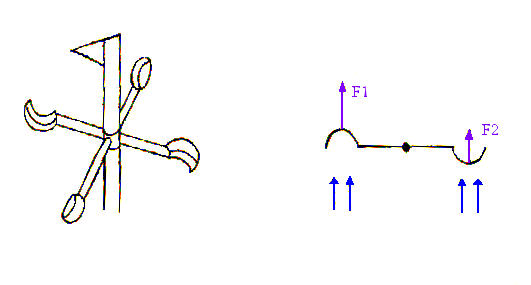
Fig. 16 – Anemometro a pressione: ruota a palette.

 

 

 

 

2. ELICA: La versione portatile del trasduttore a ruota a palette è composta da un’elica, la quale sottoposta ad un fluido in movimento ruota e per mezzo di fili di interfaccia possiamo, attraverso un apposito strumento elettronico, ottenere il valore della velocità del fluido. Questa seconda versione dell’anemometro a pressione presenta il vantaggio di poter essere facilmente spostato in più punti di un condotto e poter così effettuare misure dell’andamento della velocità W del fluido in tutto il circuito idraulico.

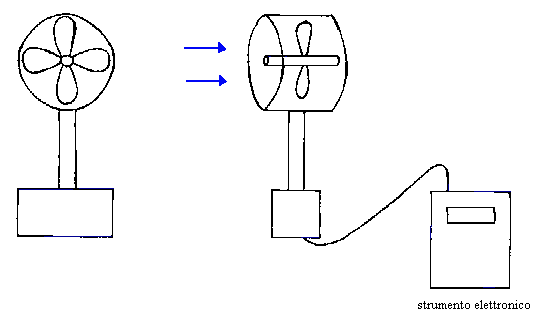
Fig. 17 – Anemometro a pressione: elica.

4. ANEMOMETRO A FILO CALDO

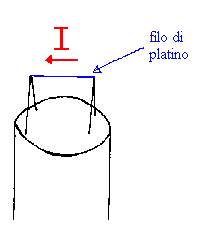
Fig. 18 – Anemometro a filo caldo.

È composto da un filo di platino nel quale viene fatta passare una corrente I. Dalla misura del rapporto fra la tensione ai capi del filo D V e la corrente I riusciamo a conoscere il valore della resistenza elettrica R:

che sappiamo essere legata alla temperatura T da una formula matematica:

Inoltre dal prodotto D V * I sappiamo il calore dissipato per effetto Joule per unità di tempo; dalle relazioni dello scambio termico si ha

Ove S è la superficie del filo, T è la temperatura del filo ottenuta dalla misura della resistenza elettrica, Tµ la temperatura dell’aria ad un’adeguata distanza, mentre R è l’incognita che abbiamo così determinato. R è definito come coefficiente di convezione ed è funzione della velocità del fluido W.

L’anemometro a filo caldo presenta il vantaggio di essere molto più piccolo rispetto ai precedenti trasduttori di portata, e quindi utilizzabile in condotti stretti, ma le ridotte dimensioni del filo di platino lo rendono molto fragile.