Trasmissione del calore
Argomenti della lezione:
Termocamera
In questa lezione si è spiegato il funzionamento della termocamera. Questo strumento è in grado di rilevare le temperature dei corpi analizzati anche se, in verità, essa non misura propriamente la temperatura T bensì la intensità di radiazione I e, di conseguenza, la quantità di calore q emessa dal corpo.
Si presentano però numerosi problemi da risolvere per la corretta gestione delle informazioni acquisite dallo strumento. Prima fra tutte la non linearità della equazione di Stefan- Boltzmann:
![]() (1)
(1)
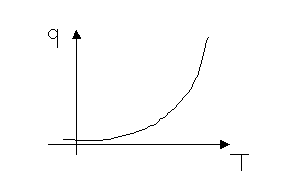
FIGURA 1: grafico qualitativo della relazione di Stefan-Boltzmann
che mi fa notare come a basse T il sistema sia impreciso. Infatti, in questa zona del grafico per discrete variazioni di T sono associati valori di q poco diversi tra loro.

FIGURA 2: immagine ripresa da una termocamera ccd
Un altro problema è dato dal fatto che la q che la macchina misura non è quella che il corpo scambia con l’ambiente ma quella che il corpo stesso emette. Per meglio dire la T del corpo analizzato è falsata dalla T degli altri corpi che lo irraggiano.
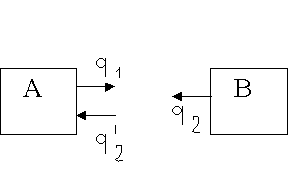
FIGURA 3: i corpi interagiscono tra loro mediante scambio termico per irraggiamento che avviene in ogni direzione
Inquadrando il corpo A con la termocamera non riesco a misurare ![]() ma rilevo per forza una quantità q , più grande, falsata dalla presenza del corpo B: misurerò quindi
ma rilevo per forza una quantità q , più grande, falsata dalla presenza del corpo B: misurerò quindi
![]()
dove a rappresenta il coefficiente di assorbimento del corpo A.
Per risolvere questa situazione si usano corpi con valori di a prossimi all’unità (in genere è sufficiente ![]() ). Se invece si ha a che fare con corpi con a molto bassi (una lastra di alluminio, con
). Se invece si ha a che fare con corpi con a molto bassi (una lastra di alluminio, con ![]() , riflette la temperatura ambiente) è necessario rivestirli di vernici particolari per raggiungere alti valori di a.
, riflette la temperatura ambiente) è necessario rivestirli di vernici particolari per raggiungere alti valori di a.
Questo sistema, se serve per misurare il q scambiato da un’aletta di raffreddamento in convezione forzata, non dà alcun problema poiché ![]() . Al contrario, dove la convezione è naturale (ad esempio un circuito elettrico), la componente
. Al contrario, dove la convezione è naturale (ad esempio un circuito elettrico), la componente ![]() diventa rilevante e la misura può risultare falsata.
diventa rilevante e la misura può risultare falsata.
Non per ultimo va infine ricordato che l’introduzione di uno strato di vernice introduce inevitabilmente una nuova resistenza termica che può fare variare la situazione dello scambio termico all’interno del corpo.

FIGURA 4: immagine ripresa da una termocamera ccd
Vediamo ora lo schema tecnico di funzionamento.
La termocamera è al suo interno autoraffreddata. Questo per raffreddare i componenti che, scaldatisi per il funzionamento, potrebbero alterare le letture dei sensori. Le moderne termocamere sono tutte del tipo CCD-MATRIX, in altre parole presentano una matrice di sensori in grado di ricevere l’immagine dell’oggetto, che è quindi scomposta pixel per pixel.
Ogni sensore della matrice presenta un suo errore di taratura, cioè ad ogni T radiante ogni sensore risponde con una tensione V differente dagli altri che può dare origine, a volte, ad errori anche di un grado. I sensori vanno quindi tarati uno ad uno. La curva di taratura, che è memorizzata dal computer all’interno della termocamera, viene costruita per punti. Si inquadra un corpo nero avente una temperatura T nota e costante e si vanno a misurare i segnali in volt forniti da ogni sensore. Questa operazione viene svolta con corpi neri a temperature diverse in modo da completare la curva di taratura con tutte le temperature che la termocamera deve essere in grado di analizzare.
Il segnale fornito in volt dai sensori è un segnale analogico. Per convertirlo in digitale nelle termocamere furono usati prima ADC a 8 bit (che forniscono 256 diverse discretizzazioni) e poi i migliori ADC a 12 bit (che ne forniscono 4096) in grado di permettere tarature raffinate anche a basse T , zona in cui le escursioni di V sono molto piccole.
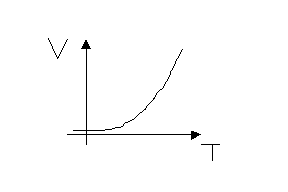
FIGURA 5 :grafico qualitativo della caratteristica della curva di taratura di un sensore
Le immagini vengono poi memorizzate nelle memory card.

FIGURA 6: immagine ripresa da una termocamera ccd
Ogni immagine, formata da 480*308 pixel, è memorizzata come fosse una matrice all’interno della quale ad ognuno dei 1824 pixel viene associato un numero (da 0 a 4095) rappresentante il valore di tensione che il sensore aveva registrato e di conseguenza ne rappresenta il livello di luminosità da adottare per la visualizzazione della immagine.
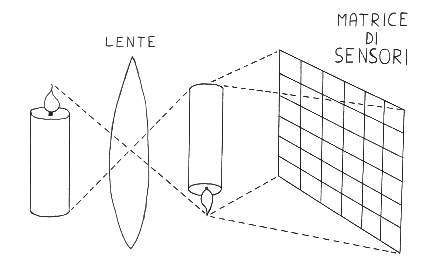
FIGURA 7: schema di funzionamento delle termocamere ccd-matrix
Prima della disponibilità di queste nuove tecnologie le termocamere erano dotate al loro interno di prismi rotanti che deviavano la luce proveniente dall’immagine inquadrata in modo tale da far pervenire all’unico sensore presente, uno per volta, tutti i raggi luminosi che descrivevano l’immagine stessa. I prismi erano due: uno verticale che ruotava velocemente spazzando l’immagine orizzontalmente ed uno orizzontale, più lento, che deviava il raggio del primo prisma verticalmente in modo tale da cominciare una nuova colonna quando il primo prisma aveva finito di spazzare un’intera riga.
Il vantaggio che subito si nota (e che ne giustifica il suo primo sviluppo) è che la presenza di un solo sensore permette la memorizzazione e la gestione di una sola curva di taratura anche da parte di un computer di bassa potenza.
Lo svantaggio però riguarda la definizione dell’immagine: essa infatti risulta essere un po’ mossa (i prismi vibrano) e leggermente sfuocata poiché mano a mano che il prisma verticale spazza una riga dell’immagine quello orizzontale inevitabilmente la abbassa alterando quindi la corrispondenza tra il raggio analizzato dai prismi e quello ricevuto dal sensore.
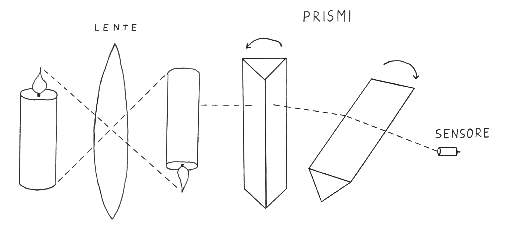
FIGURA 8: schema di funzionamento della termocamera a scansione
L’immagine che ne risulta è quindi piena di rumore, cosa che invece non accade nei sistemi CCD-MATRIX. Questi ultimi devono essere gestiti da processori più potenti ma in cambio forniscono un’immagine senza rumore, il che permette di invertire la matrice e di risalire dalla q alla T di un corpo.
Se confronto i due spettri infatti si nota subito che quello della termocamera a scansione presenta due picchi di rumore in corrispondenza delle frequenze di rotazione dei prismi.
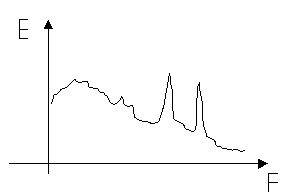
FIGURA 9:grafico qualitativo dello spettro del rumore di una termocamera a scansione. Si possono notare i caratteristici picchi generati dai prismi in rotazione. In ascissa è presente la frequenza spaziale, espressa in![]()
Nelle termocamere CCD invece il rumore si presenta mediato nel tempo: questo comporta quindi una sua progressiva attenuazione contrariamente invece al rafforzamento del segnale utile che compone l’immagine.
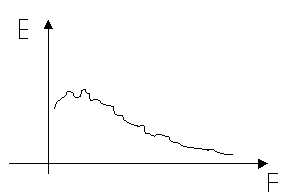
FIGURA 10: grafico qualitativo dello spettro del rumore di una termocamera ccd-matrix. In ascissa è presente la frequenza spaziale, espressa in ![]()
Esercizio
Vengono dati i parametri caratteristici del condotto verticale di un camino costituito da un foglio di lamiera non isolata e con resistenza termica nulla. Si chiede di determinare la quantità di calore Q che il condotto scambia con l’esterno e la temperatura di uscita dei fumi caldi di combustione.
I parametri sono:
Le incognite sono:
Lo scambio termico che sta avvenendo può essere schematizzato come si vede in figura 11 tramite le resistenze termiche equivalenti.
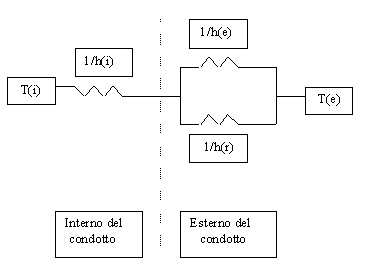
FIGURA 11
Si nota quindi come all’interno del condotto sia presente la sola resistenza di convezione rappresentata dal termine ![]() mentre all’esterno è presente, oltre alla resistenza di convezione
mentre all’esterno è presente, oltre alla resistenza di convezione![]() , anche quella derivante dall’irraggiamento da parte della parete del condotto stesso
, anche quella derivante dall’irraggiamento da parte della parete del condotto stesso ![]() .Queste ultime due possono essere sommate, sommandone le rispettive conduttanze, per ottenere un’unica resistenza che descriva lo scambio termico all’esterno del condotto nel modo seguente:
.Queste ultime due possono essere sommate, sommandone le rispettive conduttanze, per ottenere un’unica resistenza che descriva lo scambio termico all’esterno del condotto nel modo seguente:
![]()
Posso infine sommare le due resistenze (interna ed esterna) per ottenere la resistenza totale : ![]()
Questa resistenza mi permette quindi di ricavare la quantità di calore scambiato secondo la relazione:
![]()
per unità di superficie S.
Comincio quindi col ricavare il valore di ![]() . Questo valore si può ricavare dalla relazione
. Questo valore si può ricavare dalla relazione
![]()
nella quale compaiono:
![]() conducibilità termica in questo caso riferita all’aria a
conducibilità termica in questo caso riferita all’aria a ![]() (tabulata)
(tabulata)
D diametro del condotto
Nu numero di Nusselt
Per ricavare il numero di Nusselt mi servo della relazione valida per la
convezione forzata
![]()
nella quale compaiono:
a, b, c costanti
Pr numero di Prandt (per l’aria costante di valore 0,71 )
Re numero di Reynolds
Per conoscere il valore delle tre costanti devo calcolare il valore di Re tramite l’equazione
![]()
nella quale compaiono:
W velocità media dei fumi
D diametro del condotto
![]() viscosità cinematica calcolata per l’aria a
viscosità cinematica calcolata per l’aria a ![]() (tabulata)
(tabulata)
Essendo la viscosità tabulata e diametro e velocità forniti dal testo del problema, si trova facilmente
![]()
Si nota come il regime di moto del fluido sia evidentemente turbolento; devo quindi usare i valori delle costanti attribuiti dalla relazione di Dittus-Boelter e cioè a=0.8
b=0.3
c=0.023
ricavando quindi
![]()
Sono quindi in grado di calcolare ![]() dalla relazione (4)
dalla relazione (4)
![]()
Calcolo ora il valore di ![]() , che posso ottenere dalla relazione
, che posso ottenere dalla relazione
![]()
ove compaiono:
![]() conducibilità termica calcolata questa volta per l’aria a
conducibilità termica calcolata questa volta per l’aria a ![]() (tabulata)
(tabulata)
Nu numero di Nusselt
L lunghezza del condotto
Si noti come ora siamo in presenza di convezione naturale e come quindi cambi l’espressione per ricavare il valore di Nu :
![]()
nella quale non compare più Re ma compare il numero di Grashof Gr. Questo mi serve per poter determinare, come nella (5), il valore delle tre costanti a, b, c.
La relazione per ricavare Gr è la seguente:
![]()
nella quale compaiono:
g accelerazione di gravità
![]() coefficiente di dilatazione termica
coefficiente di dilatazione termica
L lunghezza caratteristica (viene adottata la lunghezza del condotto)
![]() temperatura di parete del condotto
temperatura di parete del condotto
![]() temperatura esterna
temperatura esterna
![]() viscosità cinematica
viscosità cinematica
L’unica incognita di questa equazione è rappresentata dalla ![]() . Bisogna quindi ipotizzarne il valore, per esempio
. Bisogna quindi ipotizzarne il valore, per esempio ![]() . Posso pertanto ricavare il valore di
. Posso pertanto ricavare il valore di ![]() , che per i gas perfetti vale
, che per i gas perfetti vale
![]()
Ipotizzata la temperatura di parete, per calcolare ![]() devo prima convertire i valori delle temperature da gradi Centigradi a gradi Kelvin. Posso quindi ricavare dalla (13)
devo prima convertire i valori delle temperature da gradi Centigradi a gradi Kelvin. Posso quindi ricavare dalla (13)
![]()
Ora ho tutti i valori per poter calcolare Gr . Dalla(12):
![]()
Poiché il valore Gr è maggiore di![]() il regime del fluido è turbolento e pertanto vale la relazione di Mc Adams che assegna alle tre costanti i seguenti valori:
il regime del fluido è turbolento e pertanto vale la relazione di Mc Adams che assegna alle tre costanti i seguenti valori:
a = 0.33
b = 0.33
c = 0.13
che mi permettono di calcolare Nu secondo la (11)
![]()
con il quale finalmente posso trovare il valore di ![]() con la (10):
con la (10):
![]()
Resta ora da calcolare ![]() tramite la relazione
tramite la relazione
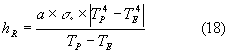
nella quale sono noti tutti i parametri:
a coefficiente di assorbimento (a = 0.8 )
![]() costante
costante ![]()
![]() temperatura esterna
temperatura esterna
![]() temperatura di parete (ipotizzata)
temperatura di parete (ipotizzata)
in questo modo ricavo
![]()
Posso calcolare, dalla (1)
![]()
e dalla (2) ![]()
per ottenere infine il primo dato richiesto dal problema. Dalla (3) ricavo
![]()
Devo però verificare la correttezza dell’ipotesi sulla temperatura di parete. Ora che conosco Q posso ricavarla dalla relazione
![]()
e ottengo ![]() . Ben diverso da quanto si era ipotizzato. Devo pertanto utilizzare ora questo valore di temperatura e iterare i calcoli, a partire dalla (10) fino a quando il valore si stabilizza. Ricavo nell’ordine i seguenti valori:
. Ben diverso da quanto si era ipotizzato. Devo pertanto utilizzare ora questo valore di temperatura e iterare i calcoli, a partire dalla (10) fino a quando il valore si stabilizza. Ricavo nell’ordine i seguenti valori:
dalla (13) ![]()
dalla (12) ![]()
dalla (16) ![]()
dalla (10) ![]()
dalla (18) ![]()
dalla (21) ![]()
dalla (22) ![]()
dalla (23) ![]()
La temperatura è ancora diversa. Ripeto un’altra volta i calcoli usando questo nuovo valore.
dalla (13) ![]()
dalla (12) ![]()
dalla (16) ![]()
dalla (10) ![]()
dalla (18) ![]()
dalla (21) ![]()
dalla (22) ![]()
dalla (23) ![]()
La temperatura è diminuita. Questo è un buon segno perché vuole dire che sta cominciando a stabilizzarsi. Itero un’altra volta.
dalla (13) ![]()
dalla (12) ![]()
dalla (16) ![]()
dalla (10) ![]()
dalla (18) ![]()
dalla (21) ![]()
dalla (22) ![]()
dalla (23) ![]()
La temperatura oscilla sempre meno. Itero l’ultima volta per ricavare il valore stabilizzato.
dalla (13) ![]()
dalla (12) ![]()
dalla (16) ![]()
dalla (10) ![]()
dalla (18) ![]()
dalla (21) ![]()
dalla (22) ![]()
dalla (23) ![]()
La temperatura si è stabilizzata. Il valore reale è ![]() e il calore scambiato è
e il calore scambiato è ![]() . Posso quindi rispondere al secondo quesito del problema: calcolare la temperatura di uscita dei fumi. Questa si trova facilmente dalla relazione
. Posso quindi rispondere al secondo quesito del problema: calcolare la temperatura di uscita dei fumi. Questa si trova facilmente dalla relazione
![]()
ove compaiono:
![]() calcolato sopra
calcolato sopra
![]() portata in massa
portata in massa
![]() calore specifico dell’aria a pressione costante
calore specifico dell’aria a pressione costante
![]() temperatura interna dei fumi
temperatura interna dei fumi
![]() temperatura di uscita dei fumi
temperatura di uscita dei fumi
La portata in massa si ricava dalla relazione
![]()
con:
![]() densità dei fumi
densità dei fumi
W velocità media dei fumi
S sezione del condotto
Prima bisogna quindi calcolare la densità. Dalla relazione dei gas perfetti:
![]()
e la portata in massa diventa, dalla (25)
![]()
Dalla (24) posso infine calcolare il secondo dato richiesto dal problema
![]()
Ora che conosco le temperature di ingresso e di uscita dei fumi posso rendere più preciso il calcolo del calore scambiato Q utilizzando un valore medio di temperatura dei fumi
![]()
ricavando in questo modo dalla (3)
![]()