Scambio termico per irraggiamento
Introduzione
Questo tipo di scambio
termico è, dopo la conduzione e la convezione , il terzo modo attraverso il
quale i corpi cedono e ricevono energia dal sistema nel quale si trovano; tale
scambio avviene attraverso l’emissione e l’assorbimento di onde
elettro-magnetiche e si differenzia dai due precedenti poiché non necessita di
un mezzo trasmissivo.
Supponiamo allora di
avere un sistema costituito solamente
da due corpi , come in fig .1, che siano separati da un mezzo trasparente alla
radiazione elettromagnetica (ad esempio il vuoto) e si trovino a due
temperature diverse:
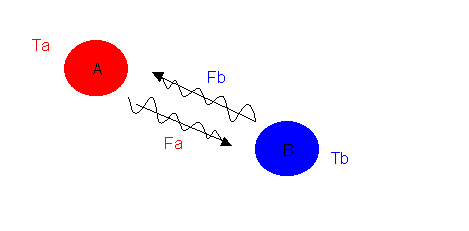
Fig.1 Scambio termico per
irraggiamento tra due corpi
Il flusso di energia tra
questi due corpi è continuo ed in generale è diverso da zero (cioè Fa ¹Fb); anche quando si raggiunge l’equilibrio
termodinamico essi continuano comunque ad emettere e assorbire radiazione.
Questo discorso vale
anche , nel caso di un corpo concavo, per le varie parti di un corpo stesso:
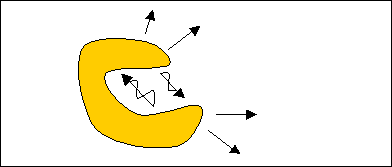
Fig.2 Scambio termico
per irraggiamento in un corpo concavo
In seguito ,per
semplicità , faremo sempre riferimento a corpi
convessi nei quali questo fenomeno non avviene.
Onde
elettro-magnetiche
La propagazione di
un’onda elettro-magnetica è descritta completamente dalle equazioni di Maxwell
in assenza di sorgenti che esprimono il legame tra la variazione del vettore
campo elettrico E e il vettore induzione magnetica B e viceversa:
(1) 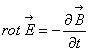 (2)
(2) 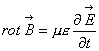
dove i vettori E e
D sono ortogonali tra loro e rispetto alla direzione di propagazione,
che è rettilinea .Come si può notare dalla presenza delle derivate rispetto al
tempo nelle equazioni (1) e (2) , non si può avere propagazione di un’onda
elettromagnetica se non si hanno valori del campo E o del campo B fluttuanti
nel tempo.Ne consegue che un oggetto fortemente carico,pur producendo un
elevato campo elettrico , non è in grado di scambiare calore per
irraggiamento.Neanche la presenza simultanea di campo elettrico e
magnetico(dovuti ad esempio ad una elettrocalamita) è sufficiente a garantire
l’emissione di onde elettromagnetiche.
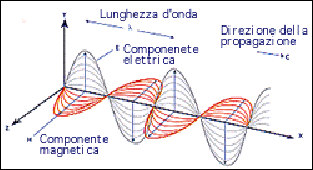
Fig.3 Propagazione di un’onda elettromagnetica
La condizione che massimizza il valore dell’energia trasportata è che i due
vettori siano in fase (come in fig.3).
La lunghezza d’onda e la frequenza sono legate dalla relazione:
(3) ![]()
dove l è lunghezza d’onda, f
la frequenza e c è la velocità della luce nel mezzo considerato; in
particolare nel vuoto essa raggiunge il suo valore massimo
![]()
Negli
altri mezzi invece tale velocità vale :
(4)
![]()
dove n è una costante tipica del mezzo nel
quale si propaga l’onda ed è detta indice di rifrazione assoluto del mezzo. Non
esistono mezzi nei quali n è minore di uno,cioè la luce nel vuoto si
propaga con la massima velocità possibile.
La tabella che segue mostra alcuni indici di
rifrazione rispetto al vuoto, per l=589nm (riga gialla del sodio):
|
Mezzo materiale |
Indice |
Mezzo materiale |
Indice |
|
Aria(c.n di T e p) Acqua(20°C) Fluoruro di sodio Acetone Alcool etilico Soluzione di zucchero(30%) Quarzo fuso Soluzione di zucchero(80%) |
1.000029 1.33 1.33 1.36 1.36 1.38 1.46 1.49 |
Normale vetro crown Cloruro di sodio Polistirene Bisolfuro di carbonio Vetro flint denso Zaffiro Il più denso vetro flint Diamante |
1.52 1.54 1.55 1.63 1.65 1.77 1.89 2.42 |
Fig.4
Alcuni indici di rifrazione rispetto al vuoto per l=589nm.
Le onde elettromagnetiche vengono poi suddivise e
classificate in base alla loro lunghezza d’onda :
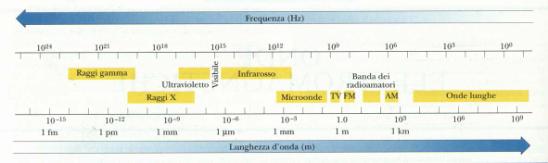
Fig.5
Lo spettro elettromagnetico
Come si può osservare la luce visibile è solo una
riga sottilissima dell’intero spettro che si estende intorno alla l=550nm.
Considerazioni energetiche
Per quanto riguarda il trasporto di energia da parte di un’onda elettromagnetica ,esso avviene ad ogni lunghezza d’onda.Occorre però fare distinzione tra le varie bande poiché ,a valori “normali” di campo, gli effetti predominanti su un corpo investito dalla radiazione possono essere molto diversi .Il fenomeno che a noi interessa è quello dello scambio termico di energia.
Ad esempio per l’ultravioletto , raggi X, raggi g e radiazione cosmica già a valori modesti di
campo si osservano forti effetti ionizzanti che tendono a danneggiare
componenti organici pur non provocandone un sensibile riscaldamento.
Per quanto riguarda invece le onde radio, per
avere una variazione di temperatura apprezzabile, occorre investire il campione
con valori di campo elevatissimi.
Per le onde di Hertz invece (50 Hz<f <1000
Hz) il problema principale è il valore della frequenza che può interagire con
alcuni meccanismi biologici che regolano il sistema nervoso;anch’esse però non
contribuiscono efficacemente allo scambio termico.
Per tutte queste ragioni ci si occupa degli
effetti termici praticamente solo per le microonde , la luce visibile e
l’infrarosso.
A questo
proposito è perciò opportuno dare alcune definizioni di grandezze che ci
aiuteranno a capire quale sia la quantità di energia scambiata da un corpo per
irraggiamento.
Spettro di emissione
Fino ad ora abbiamo
considerato solamente onde monocromatiche, quella che in acustica
chiamiamo toni puri, sinusoidi ad una
ben determinata frequenza.
Sono poche le sorgenti di
radiazione elettromagnetica che emettono questo tipo di radiazioni, una delle
quali è la lampada laser.
Gli altri corpi emettono simultaneamente su
un ampio spettro di frequenze, compiendo una cosiddetta emissione in banda
larga.Questo accade poiché ogni elemento ha un numero finiti di stati
elettronici eccitabili che corrispondono a diverse lunghezze d’onda che possono
essere emesse; quando si ha a che fare con un elemento singolo si osservano
quindi delle righe isolate mentre più in generale quando si ha a che fare con
un corpo composito lo spettro di emissione è solitamente continuo, a banda
larga e presenta dei picchi corrispondenti agli elementi che lo costituiscono.
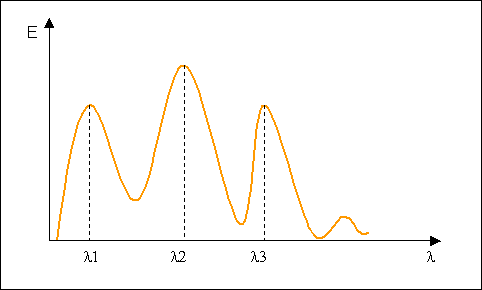
Fig. 6 Spettro di emissione di un corpo generico
Spettro di assorbimento
Supponiamo di avere un
materiale semitrasparente sul quale incide una radiazione elettromagnetica
“bianca”(cioè con intensità Ii costante a tutte le frequenze); in
generale parte di essa verrà trasmessa( It) mentre la restante verrà
in parte riflessa(Ir), in parte assorbita(Ia).
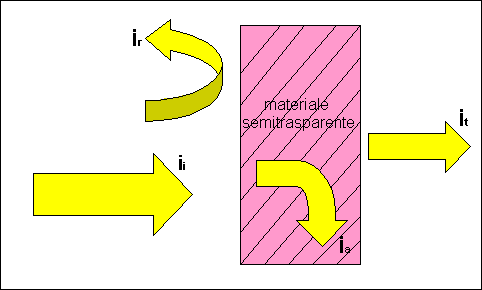
Fig.7 Comportamento della radiazione elettromagnetica
Se si va a misurare la quantità di energia trasmessa e la si va a disegnare in funzione della lunghezza d’onda si trova lo spettro di assorbimento del materiale.Tale spettro sarà il duale di quello di emissione cioè si troveranno dei minimi in corrispondenza delle lunghezze d’onda alle quali si aveva il massimo di emissione e viceversa.
Siamo di fronte ad un fenomeno simmetrico: l’elettrone che da uno stato eccitato si porta in una condizione di minore energia emette un fotone ad una determinata lunghezza d’onda, ma nel momento in cui sotto l’azione di una luce bianca è eccitato assorbe un fotone alla stessa frequenza, caratteristica della particolare transizione.
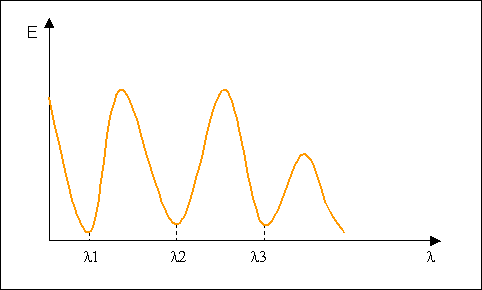
Fig.8 Spettro di
assorbimento dello stesso materiale di fig.6
Corpo Nero
Qualunque corpo che si trovi ad una temperatura
diversa dallo zero assoluto emette una
certa quantità di energia che in generale è diversa per corpi diversi.Il corpo
nero è definito come quel corpo che è in grado di emettere più energia di
qualsiasi altro.
In generale lo spettro di emissione di un
materiale ad una certa temperatura in funzione della lunghezza d’onda presenta
un andamento curvilineo con diversi massimi e minimi:
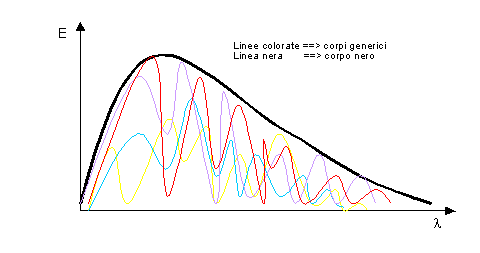
Fig. 9 Spettri di emissione di corpi diversi tutti
alla stessa temperatura
(ogni linea di diverso colore rappresenta lo spettro di un corpo)
Lo spettro di emissione del corpo nero si ottiene dall’inviluppo di infiniti spettri di corpi diversi poiché nessun corpo ,ad una qualsiasi lunghezza d’onda, può emettere più energia di esso.
Una definizione alternativa di corpo nero (vista la reciprocità tra spettri di emissione e assorbimento) potrebbe anche essere quella di corpo che colpito da una radiazione è in grado di assorbirla completamente.
Anche se sembra solo una astrazione matematica il corpo nero può essere realizzato con buona approssimazione attraverso una cavità di materiale con buona conducibilità termica e pareti interne il più possibile opache alla quale si possa accedere solo attraverso un piccolo foro sulla superficie.
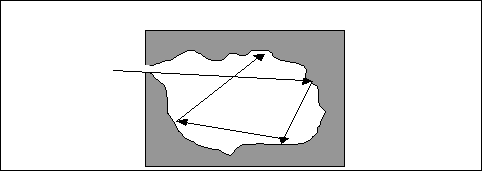
Fig.10 Esempio di corpo nero
Il piccolo foro sulla superficie, dal quale la radiazione entrante non riesce più ad uscire poiché dopo varie riflessioni all’interno della cavità viene assorbita dal materiale, può essere un buon esempio di corpo nero.
Inoltre, facendo riferimento alla fig.7, definendo:
(5) ![]() Coefficiente di
assorbimento
Coefficiente di
assorbimento
(6) ![]() Coefficiente di
riflessione
Coefficiente di
riflessione
si può anche contraddistinguere il corpo nero osservando che per esso e solo per esso a=1 e r=0.
I corpi non neri vengono detti colorati poiché emettono(assorbono) in modo differente alle diverse lunghezze d’onda e quindi sono distinguibili per il “colore” maggiormente emesso (assorbito).
Grandezze energetiche caratteristiche
E’ necessario introdurre alcune grandezze specifiche che permettano di quantificare la quantità di energia scambiata da un corpo per irraggiamento.
Detta
q la potenza emessa per unità di superficie ( W/m2 s)(si può
osservare per quanto detto precedentemente che essa è funzione della
temperatura), si definisce il potere emissivo monocromatico o specifico
q| come
(7) ![]() (W/m3s)
(W/m3s)
ed
esso rappresenta la quantità di energia emessa per un certo intervallo unitario
di lunghezza d’onda
Allora sarà
(8) ![]()
e q viene detto perciò potere
emissivo integrale, in quanto rappresenta la quantità totale di energia
emessa su tutto lo spettro.
Leggi del corpo
nero
Legge di Stefan-Boltzmann
Questa legge lega tra loro la quantità totale di energia emessa da un corpo
nero q0 alla temperatura, in gradi Kelvin, alla quale esso si trova
tramite la semplice relazione:
(9) ![]()
dove
![]() è detta costante
di Stefan-Boltzmann .
è detta costante
di Stefan-Boltzmann .
Per
quanto detto in precedenza, per ogni corpo che non sia nero ,varrà perciò
sempre la relazione q<q0.
Definendo
poi emissività monocromatica il rapporto:
(10) ![]()
si può notare come per un corpo generico essa sia
una quantità variabile al variare della lunghezza d’onda mentre per il corpo
nero sia costante e uguale a 1.
Se per un corpo vale che l’emissività
monocromatica è costante ma diversa da 1
(può essere soltanto minore) allora esso viene chiamato corpo grigio e
vale ancora la legge di Stefan-Boltzmann corretta da tale coefficiente.
(11)
![]()
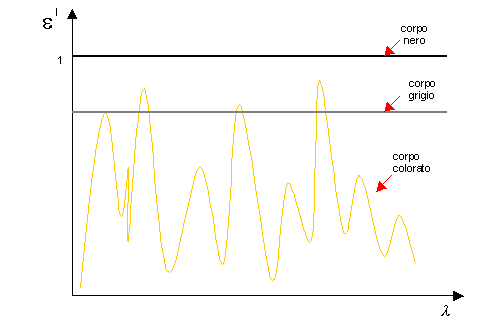
Fig.11 Andamento dell’emissività monocromatica in funzione di l
Corrispondenza tra effetti emissivi e assorbenti
Come è già stato fatto quando si parlava di spettri di emissione e di assorbimento, anche ora si vuole mettere in luce la corrispondenza tra questi due effetti; ciò è possibile tramite il semplice esperimento illustrato qui di seguito:
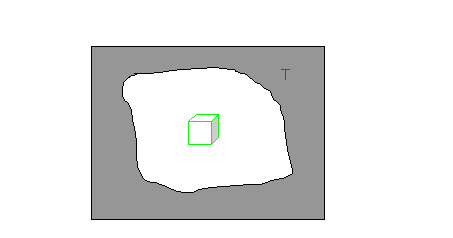
Fig.12 Corpo inserito in una cavità isoterma
Se inseriamo un corpo in
una cavità isoterma possiamo osservare come esso si porti più o meno velocemente
alla stessa temperatura della cavità e venga a trovarsi in equilibrio
termodinamico con il sistema; questo perciò implica che il corpo a regime
emette tanta energia quanta ne assorbe.
Tutto ciò può però
accadere solo se
(12)
e|(l)=a|(l)
dove con a|(l) =a(l)\a0(l) si può indicare l’assorbività monocromatica.Se
non valesse la (12) nessun corpo raggiungerebbe mai l’equilibrio
termodinamico!Quindi spesso si parla solamente di spettri e coefficienti di
assorbimento tralasciando volutamente le caratteristiche di emissione che sono
comunque già note date le prime.
Legge di Planck
Questa legge afferma che
il potere emissivo specifico di un corpo nero è esprimibile nella forma
(13) ![]()
dove le due costanti c1
e c2 valgono rispettivamente:
![]()
![]()
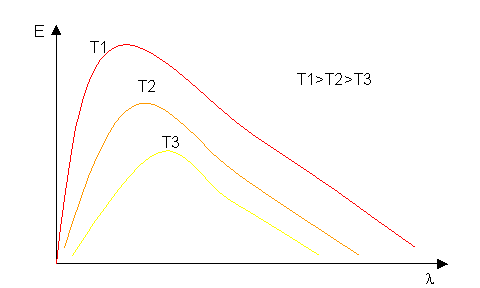
Fig.13 Spettri di emissione di un corpo nero ricavati dalla Legge di Plance
Questa espressione si ottiene
approssimando il corpo emettitore ad un insieme di oscillatori armonici e
sposando la fisica quantistica, che associa ad essi dei livelli energetici
discreti.
Legge di Wien
Come si vede dalla fig.13
lo spettro di emissione di un corpo nero presenti un massimo. Questa legge
mostra come la lunghezza d’onda alla quale si presenta il massimo diventa
sempre più piccola all’aumentare della temperatura. Tale comportamento è
descritto dalla seguente relazione detta Legge di Wien:
(14) ![]()
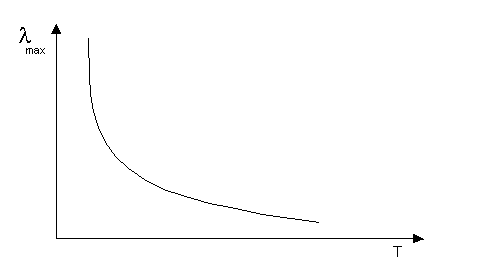
Fig.14 Legge di Wien
Tale relazione può essere
ricavata derivando la legge di Planck rispetto alla lunghezza d’onda e può
essere rappresentata graficamente come illustrato in fig.14.
Il massimo delle curve
diventa sempre più marcato e si sposta verso le alte frequenze al crescere
delle temperature, cioè dall’infrarosso tende a spostarsi verso il visibile;
questo spiega perché i corpi freddi non emettono nulla nel visibile,mentre
quando si scaldano diventano luminosi.
Nasce
cosi il concetto della temperatura di colore cioè della temperatura alla
quale devo portare il corpo nero per emettere uno spettro simile il più
possibile a quello del corpo che considero .Tale concetto in gergo fotografico
è stato oggetto di fraintendimenti in quanto si dice calda una luce con componenti vicine al rosso (che in realtà
sono fredde),mentre si definiscono luci fredde quelle vicino al blu che in
realtà sono ben più energetiche.
Attraverso
tale parametro posso dare una stima qualitativa della bontà di sistemi di
illuminazione , infatti tanto più la temperatura di colore si avvicina a quella
della luce solare (5500K ) tanto più l’illuminazione è migliore.Non è comunque
detto che due corpi con la stessa temperatura di colore abbiano lo stesso
effetto cromatico;per la lampada al neon ad esempio che si avvicina molto ai
5500k è ben nota la scarsa qualità. Tale concetto viene inoltre utilizzato
durante la scelta di pellicole fotografiche per ottenere una resa che sia la
migliore possibile.
Legge di Prevost
In pratica la legge di Prevost è una conseguenza del primo principio della
termodinamica applicato allo scambio termico per irraggiamento; essa afferma
che a regime la potenza scambiata da un corpo qs è uguale
alla potenza emessa qe meno quella ricevuta qr cioè:
(15) ![]()
Ricordando poi che la quantità di energia ricevuta è uguale a quella incidente
qi moltiplicata per il coefficiente di assorbimento a si
ottiene:
(16) ![]()
Legge di Lambert
Questa legge descrive il
comportamento angolare dell’emissione del corpo nero e rende conto dell’anisotropia
di tale fenomeno. Per descrivere tale fenomeno occorre introdurre il concetto
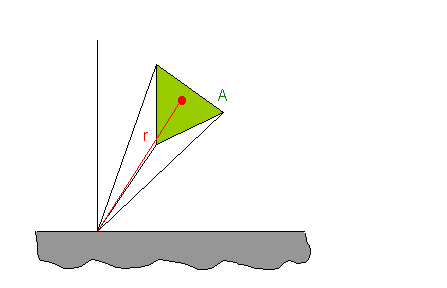
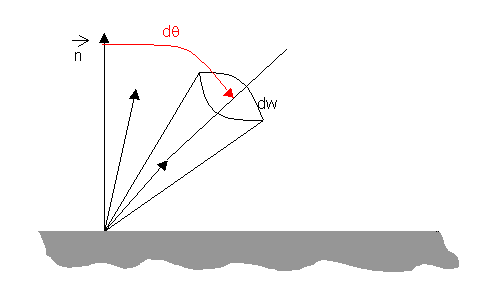
di potere emissivo integrale i definito come la potenza emessa per unità
di superficie su un angolo solido dw, cioè
Fig.16 Potere emissivo integrale
Il potere emissivo
angolare viene convenzionalmente rappresentato in coordinate polari:
l’inviluppo delle sue ampiezze è detto solido fotometrico.
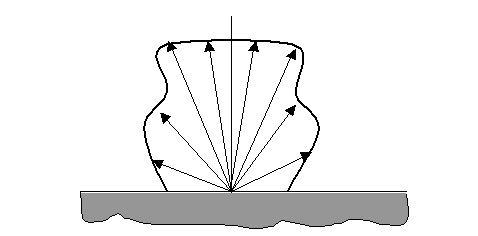
Fig. 17 : Esempio di solido fotometrico
In questi diagrammi
l’angolo con l’orizzontale rappresenta la direzione di emissione, la distanza
della curva dall’origine rappresenta l’ampiezza del potere emissivo angolare. Spesso essi sono simmetrici rispetto all’asse
verticale, ma non è la regola.
La legge di Lambert
descrive l’andamento di i(q) per
il corpo nero dove q è l’angolo indicato in fig.16. e im è il massimo di emissione
che viene raggiunto in direzione normale alla superficie di emissione; tale
legge dice che:
(19)
![]()
Il solido fotometrico
corrispondente è perciò una circonferenza:
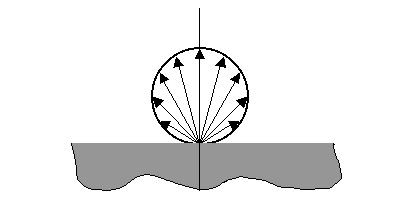
Fig.18 Solido fotometrico del corpo nero
Purtroppo però per gli altri corpi non è possibile ricavare relazioni
altrettanto semplici poiché in generale i solidi fotometrici hanno forme molto
più complesse.