ACUSTICA NEGLI SPAZI CHIUSI

 

 

In questo capitolo vedremo quali sono i fattori che influenzano il comportamento di una suono all’interno di un ambiente chiuso (es. una stanza) e quali sono le formule con cui si legano questi fattori.

 


 


                                 S  ____________________________    R

                                                              d

 

Fig. 1 – Propagazione del suono

 

 

Data una sorgente  S di suono a una certa distanza d dal ricevitore R, l’espressione che lega il livello di pressione a una certa distanza dalla sorgente è:

 

Lp = Lw – 20 log ( d ) – 11 + 10 log ( Q )      

 

Q = direttività della sorgente.

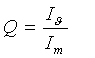  Iθ intensità nella direzione, Im intensità omnidirezionale

 

Dipende da come è posizionata la sorgente :

 

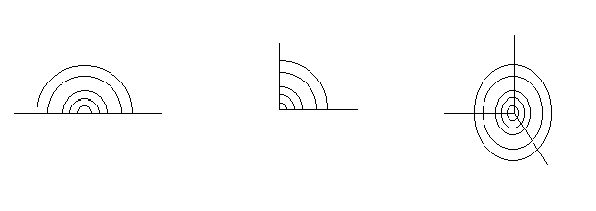Q=2Q=8Q=4 Fig. 2 – Direttività della sorgente

 

 

 

 

Immaginiamo una sorgente in uno spazio aperto.

 

                                       

 

 

 

 


                                                 S                      d                      R

 

Fig. 3 – Propagazione del suono in uno spazio aperto

 

 

Le onde sonore emesse dalla sorgente (S) si diramano in tutte le direzioni e giunge al ricevitore (R) solo l’onda DIRETTA ( cammino di propagazione diretto, percorso dall’onda sonora senza subire alcuna riflessione, che si ottiene congiungendo idealmente con un tratto rettilineo la sorgente e il ricevitore).

 

In una spazio chiuso (es. stanza)

 

 

 

 

Fig. 4 – Propagazione del suono in uno spazio chiuso

 

Vi sono raggi che urtano le pareti (onda riflessa dalla parete)e arrivano al RICEVITORE dopo un certo tempo, oltre all’onda DIRETTA .

Non possiamo più applicare la formula di prima (valida solo per l’onda diretta).

 

 

RITARDO

Se facciamo un grafico riguardo l’energia che arriva al ricevitore rispetto al tempo impiegato:              

                                           E

 

 

 

 

 

 


                                                                                           

                                                                                            T

Fig. 5 – Energia al rivcevitore

 

Numero riflessioni medie:     n (t) = 4p C²t³

                                                         V

 

Con C velocità media del suono nell’aria e V volume dell’ambiente.

Si vede come n dipenda da t (le linee verticali del grafico si infittiscono col passare del tempo).

La prima linea, quella più alta, rappresenta l’onda diretta, le altre le onde riflesse che impiegano più tempo per giungere al ricevitore e quindi dissipano una maggiore energia durante il tragitto.

Per vedere come si riflettono le onde contro le pareti:

 

 

 

 

 

 

 

 

 

 


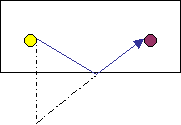
                                                              S’

Fig. 6 – Riflessione di onde contro le pareti

 

Per calcolare il cammino ci si riferisce alle SORGENTI IMMAGINE.

Costruiamo una sorgente immagine S1 specularizzando la sorgente reale rispetto a una delle pareti. Attraverso semplici considerazioni geometriche, siamo in grado di tracciare il percorso seguito dall’onda sonora, trovando così un cammino riflesso. La lunghezza del cammino riflesso è esattamente uguale alla distanza tra la sorgente immagine S1 e il ricevitore.

 All’aumentare del numero delle sorgenti immagine, avvengono due fatti importanti:

-                 aumenta la distanza della sorgente dal ricevitore e, di conseguenza, diminuisce il contributo energetico del singolo raggio riflesso;

-                 il numero totale di raggi riflessi cresce in modo esponenziale. (fig. 5)

 

In S’ l’onda è attenuata dall’assorbimento della parete.

Potremmo calcolare tutta l’energia E che arriva al ricevitore R se applico il calcolo e analizzo tutte le onde.

E’ quello che fanno certi software.

In questo modo si calcola la pressione finale del ricevitore.

 

EQUAZIONI CHE REGOLANO GLI AMBIENTI CHIUSI

 

Gli ambienti si dividono in due categorie: RIVERBERANTI e SEMIRIVERBERANTI.

Hanno diverse equazioni per descrivere i comportamenti del suono al suo interno.

 

  1. Ambienti riverberanti

 Le pareti hanno coefficienti d’assorbimento nullo.

L’E emessa resta nell’ambiente (conservazione).

Il raggio verrà attenuato per il cammino percorso e l’aria.

Il livello di pressione è uguale in tutti i punti e non c’è livello d’intensità (è relativo allo spostamento di pressione).

Sono camere di forma non regolare (si potrebbero creare onde con picchi di massimi o minimi di pressione (per sovrapposizione di onde) ), dimensioni non elevate (2x3 m) e rivestite di materiali isolanti al suono.

Queste camere utilizzate negli esperimenti sul suono sono ambienti SABINIANI, cioè caratterizzati da dimensioni confrontabili e sono utilizzate per determinare il coeff. di certi materiali.

 

  1. Ambienti semiriverberanti

       Le pareti assorbono più o meno parte delle onde emesse dalla sorgente con    

      conseguente perdita di energia.

 

PARAMETRI

 

Definiamo dei parametri che ci aiuteranno a chiarire il comportamento del suono nell’ambiente.

 

Tr tempo di riverbero

Lm libero cammino medio

ά coefficiente d’assorbimento medio dell’ambiente

 

 

Tr

 

In ambiente riverberante Tr è molto alto, anche 2-4 secondi.

Si può misurare il Tr di un ambiente in due modi:

 

·        Metodo che sfrutta il regime stazionario interrotto

Data una sorgente omnidirezionale (di solito un dodecaedro con 12 altoparlanti) nell’ambiente, si accende e si aspetta che l’ambiente si saturi del suono.

A questo punto si spegne bruscamente.

 

 

                                                                              Er                                                Er

                                                                              saturazione                                   Spegnimento

         E

 

 

 

 

 


                                                                           t                                                                           t                                                                           t    

Fig. 7 – Variazione di energia al ricevitore

 

Accensione: il campo sonoro si mantiene al livello L0 = LW–11–20lg r, finché arriva la prima onda riflessa, poi il livello totale si trova sommando i livelli del suono diretto e del suono riflesso.

Trascorso un ulteriore ritardo, inferiore a quello precedente, arriva un altro suono riflesso e il livello totale aumenta di un altro gradino. I suoni riflessi successivi giungono sempre più ravvicinati: il livello totale non ha più un andamento a gradini, ma aumenta in modo continuo, seguendo una curva che tende al valore di regime Lreg. Questo valore viene raggiunto quando si stabilisce un bilancio tra l’energia emessa dalla sorgente e quella assorbita dalle pareti.

 

Spegnimento: dal momento in cui viene spenta la sorgente, trascorre di nuovo un tempo t0 affinché il livello totale cominci a scendere: si esaurisce per primo il contributo del suono diretto e si ha un piccolo gradino, perché ora il grosso dell’energia è dovuto al suono riflesso; successivamente, scompaiono i contributi dei suoni riflessi.

 

Quindi al momento dello spegnimento vi è un brusco calo di energia al ricevitore (calo di pressione).

 

 

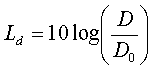
Con D0 densità sonora.

 

Il persistere per un certo tempo del suono nell’ambiente, dopo che l’evento sonoro è terminato, viene chiamato fenomeno della coda sonora o riverberazione.

Nel 1902, W. C. Sabine diede la seguente definizione di tempo di riverbero, o durata convenzionale della coda sonora: data una sorgente stazionaria interrotta, il tempo di riverbero è il tempo che intercorre tra l’istante in cui si esaurisce il suono diretto e l’istante in cui il livello sonoro è sceso di 60 dB; esso viene indicato con T60.

 

 


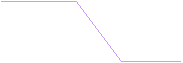
                              dB                                     regime stazionario

 

                                          -5                                                                                     Tr = T60

60 dB                                                         regime transitorio

                                       -65                                                              

 

 

                                                                                                         t

                                                                               Tr

 

Fig. 8 – Tempo necessario affinchè il livello sonoro decada di 60 dB

 

Spesso non si riesce a fare (60 decibel è un’escursione molto elevata).

Allora si considerano due o più intervalli di minore escursione:

 

30 dB (da –5 a –35)       à                T30

20 dB (da –5 a –25)       à                T20

 

Preso l’intervallo di 20 o 30 dB, si ipotizza costante la pendenza e si allarga l’intervallo fino a 60 dB.

           

 

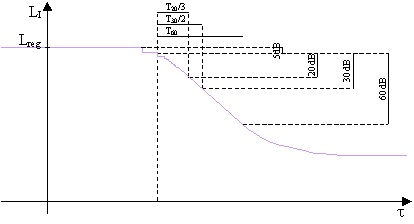
Fig. 9 – T60, T30, T30

 

 

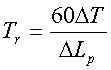
·        Analisi della risposta dell’ambiente all’impulso

È il metodo più utilizzato e più rapido.

Misuriamo la cosiddetta risposta impulsiva, cioè l’uscita del sistema in corrispondenza dell’eccitazione impulsiva X(t)=d(t), dove con d(t) indichiamo la funzione generalizzata impulso unitario, nota anche come delta di Dirac. Questo particolare impulso è riproducibile in modo approssimativo con un colpo di pistola o con lo scoppio di un palloncino d’aria.

Convenzionalmente la risposta impulsiva viene indicata con h(t). Abbiamo quindi che:

 

 

Il segnale di uscita può essere calcolato attraverso la convoluzione del segnale di ingresso con la risposta impulsiva.

Dato l’impulso d’ingresso X(t), registrando e analizzando il segnale in uscita Y(t) si può ricavare la risposta dell’ambiente h(t) tramite il procedimento di integrazione all’indietro di Schroeder.

 

 


                                                             h(t)

                    X(t)= δ(t)                                                              Y(t)

 

Fig. 10 – Analisi di un segnale

 

 

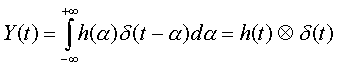
Il difetto di utilizzare strumenti come la pistola è che non tutte le frequenze sono sollecitate, il risultato può variare da esperimento a esperimento, ma gli aspetti positivi sono che è uno strumento molto semplice da utilizzare e da trasportare, nonchè la velocità del metodo.

 

Spesso al posto del segnale impulsivo delta di Dirac sono utilizzati anche altri tipi di segnali, in particolare :  i segnali MLS e una sinusoide sweeppata ( Sine Sweep ).

Vediamoli in breve.

-Segnali MLS

Il segnale MLS (acronimo di Maximum Length Sequence) è una sequenza binaria del tipo riportato in Figura 6.

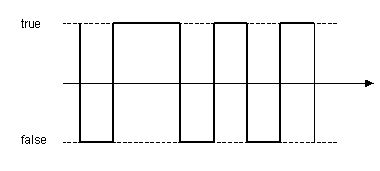
Fig. 11 –Segnale MLS

Questo segnale oggi può essere ottenuto da un qualunque personal computer mediante un software dedicato, che implementi uno shift register(registro  a scorrimento), ma fino a poco tempo fa venivano utilizzate delle schede che implementavano per via hardware lo shift register, tra queste schede è famosa quella costruita nel 1989 dall’americano Douglas Rife, e corredata da un software chiamato MLSSA (melissa) particolarmente potente, tanto da essere tuttora usato.

I vantaggi principali che ci derivano dall’uso di un segnale MLS sono innanzitutto la semplicità di calcolo del segnale inverso, essendo noto il segnale a priori, è sufficiente applicare l’operazione di inversione di Hadamard per ottenere il segnale MLS-1. Il grosso limite nell’uso di questo segnale è dovuto alla forte dipendenza dalla linearità del sistema: anche con altoparlanti estremamente fedeli è sufficiente il surriscaldamento dei trasduttori per introdurre nel sistema forti non-linearità.

-Segnali Sine Sweep

Lo SWEEP è, come noto, un segnale composto da un tono puro la cui frequenza aumenta nel tempo con un certo andamento. Attualmente il segnale che si preferisce utilizzare è un seno il cui argomento parte dalle frequenze più basse e giunge fino alle più alte.

 

 

La risposta all’impulso dell’ambiente si ottiene dalla convoluzione del segnale di risposta con lo SWEEP inverso.

In base al tipo di relazione che governa la crescita della frequenza si possono distinguere segnali  Sine Sweep di tipo:

 

1.      Lineare

2.      Logaritmico

Generalmente la preferenza ricade sui segnali di tipo logaritmico perché questi

hanno il pregio di fornire più energia nella regione delle basse frequenze, che rappresenta una zona critica, e di procedere più speditamente nella regione delle alte frequenze. Inoltre lo spettro di un segnale Sine Sweep logaritmico assomiglia molto a quello di un rumore rosa, ed ha quindi il vantaggio di essere più gradevole all’ascolto rispetto al rumore bianco.

L’unico inconveniente è che questo tipo di segnale cade di 6dB per ottava, ma il problema si risolve facilmente equalizzando il segnale.

Osserviamo, inoltre che i segnali Sine Sweep hanno una interessante caratteristica: l’inverso di questo tipo di segnale è lo stesso segnale invertito sull’asse dei tempi, secondo la tecnica Time Reversal Mirror.

L’unica controindicazione nell’impiego di questo segnale è la potenza di calcolo che esso richiede. L’operazione di convoluzione, infatti, non trae nessun vantaggio dall’utilizzo di questo segnale, e presenta quindi la ben nota complessità di calcolo. Per questa ragione, infatti, si è incominciato ad utilizzare questo segnale solo in tempi recenti, ossia da quando gli elaboratori hanno messo a disposizione maggiore potenza di calcolo.

 

 

Se in un ambiente non possiamo misurare il Tr si può comunque provare a stimarlo.

Con i dati:       A assorbimento equivalente dell’ambiente          

              ( a coefficiente di assorbimento per ogni parete i ci da una misura della quantità di onda sonora che viene ritrasmessa dopo l’urto e tiene quindi conto sia della percentuale di onda assorbita, sia della percentuale che viene ritrasmessa dalla parte opposta; Si area della rispettiva parete i; V volume proprio dell’ambiente ) .

 

I valori ottimali di Tr dipendono dall’uso a cui è finalizzato l’ambiente:

 

 

Ambiente

Topt (secondi)

Aula scolastica piccola

0,5

Aula scolastica grande

1

Cinema

0,7 ÷ 0,8

Teatro d’opera (musica lirica)

1,3 ÷ 1,5

Sala da concerto (musica sinfonica)

1,7 ÷ 2,3

Chiesa (musica sacra)

2,5 ÷ 5

 

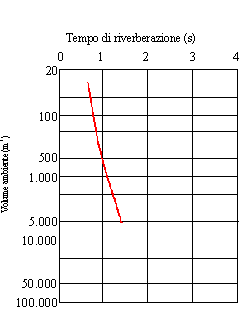
      Fig. 12 – Valori ottimi del tempo di riverberazione

 

Anche ambienti con stessi Tr possono avere dei comportamenti diversi: questo parametro non basta a descrivere tutta l’acustica dell’ambiente.

 

 


                                                           Non c’è riverbero, l’ascolto è migliore perchè

                                                           non ci sono onde riflesse.

 

 

 

 


                                                           L’ascolto è peggiore, vi è dell’ eco.

 

 

 

 


      Fig. 13 – Posizioni di altoparlanti

 

 

 

 

FORMULE CHE DECRIVONO L’ANDAMENTO DELLA PRESSIONE AL RICEVITORE

 

 

 

 


S                             Parete fonoassorbente

 

 

Fig. 14 – Camera con una parete fonoassorbente

 

Accendiamo la sorgente e aspettiamo che l’energia nell’ambiente arrivi a regime. Tutta l’energia emessa viene assorbita dall’unica parete fonoassorbente.

 

Lm : cammino che il raggio percorre tra due riflessioni consecutive

 

 

tm : tempo tra due riflessioni

 

con S superficie interna dell’ambiente e C velocità del suono .

 

Vediamo come esempio un rubinetto che riempie un contenitore: a regime l’acqua inizia con il riempire il recipiente e successivamente fuoriesce da esso.

Così le onde saturano la stanza e se la sorgente continua e emetterne queste nuove finiscono per essere tutte assorbite dalla parete fonoassorbente.

 

La variazione di energia è data dai fattori:                    dE = Es – Eα

 

Ne deriva che l’energia Es, che è l’energia assorbita dalla parete è data dall’equazione:

                                                 Es = dE + Eα

 

Un’altra grandezza molto importante nello studio dell’acustica è la densità di energia, misura che si indica con D o a volte anche con w.

Si misura in .

 

In regime stazionario        E=D V       , ma nel caso che stiamo studiando:

 

 

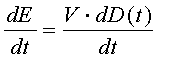
Per un dato istante tm nella stanza:

                  

 

                       

 

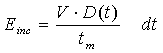
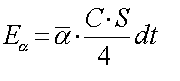
con          

 

La potenza così risultante è:

 

 

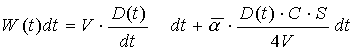
Semplifichiamo:

        (densità di energia a regime)

            

 

 

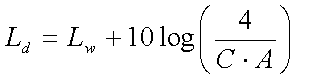
In campo riverberante il livello di pressione rispone a questa equazione:

 

 

 

In questo tipo di campo è importante sia l’onda diretta che la riflessa(l’energia al ricevitore dipende da entrambe).

Si può riscrivere anche in questa forma:

 

 

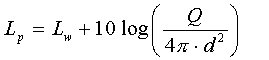
In ambiente semiriverberante Lp può essere visto come somma di due termini:

 

 

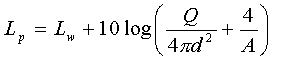
(contributo dell’onda diretta e dell’ambiente riverberante).

 

 

 


                                                 Lp     livello riverberante

 

                                                                                          livello diretto

 

 

 


                                                                                                      d = | S R |

Fig. 15 – Contributi al livello di pressione

 

Sommando trovo il livello di pressione nella stanza.

 

 


                                          Lp    

 

                   

 

 

 


                                                                                                      d

Fig. 16 – Livello di pressione in amb. Semiriverberante

 

Il punto d’incontro delle due rette si chiama distanza critica e si indica con Dc (distanza alla quale il livello del campo diretto e il livello del campo riverberante assumono lo stesso valore, cioè Ldir = Lreg ).

                 

 

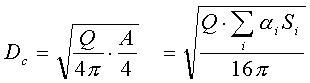
Se si lavora sulla distanza o sul comportamento dell’ambiente si può regolare Lp.

Ad esempio si può “inscatolare” la sorgente (es. macchina rumorosa in una fabbrica) così da confinarne il rumore, oppure si possono aggiungere nell’ambiente degli elementi assorbenti.

 

ESERCIZIO

Tramite le formule precedenti possiamo scoprire come si comporta il suono in una stanza.

Avendo T ricavo A dalla formula inversa di   

Q è noto dalla posizione della sorgente, quindi possiamo trovare Lp dalla formula:

                          

Purtroppo spesso se confrontiamo i dati trovati con quelli sperimentali, noteremo come non coincidano.

 

Come ricavare T60

Date le equazioni sopra trovate, cerchiamo un'altra forma dell’equazione per trovare Tr, in particolare T60.

                         

                                                                                  

                

 

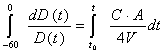
Per trovare T60 prendiamo 

 

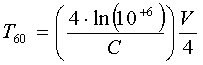
Negli ambienti riverberanti a volte:

                                     

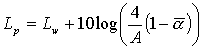
In generale il termine  viene ignorato.