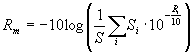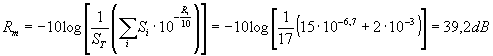Isolamento acustico, legge di massa
Argomenti trattati:
Coefficienti di riflessione, assorbimento e trasmissione
Materiali fonoassorbenti e fonoisolanti
Problemi di disturbo
Materiali fonoassorbenti
- Materiali porosi
- Risuonatori acustici
- Risuonatori di Helmholtz
- Pannelli perforati
- Pannelli vibranti
Potere fonoisolante
- Legge di massa
- Deviazioni dalla legge di massa
Esercizio
Introduzione
Quando è impossibile per ragioni economiche ridurre alla sorgente il rumore fino ad un livello accettabile, si ricorre all’isolamento acustico. L’isolamento si può ottenere sfruttando o l’assorbimento acustico o la riduzione della trasmissione acustica.
È importante determinare il comportamento sotto il profilo acustico dei materiali normalmente impiegati nell’edilizia; più in particolare quelli preposti alla realizzazione di pareti esterne, pareti divisorie, finestrature, porte, soffitti, ecc. In questo modo si può valutare l’entità del livello sonoro che si produce in ambiente come conseguenza di fonti di rumore esterne all’edificio o situate in locali prossimi a quello in esame.
Analogamente, in base al tipo di attività prevista in un dato ambiente ed ai relativi requisiti acustici, si può risalire alle caratteristiche acustiche dei materiali da impiegare al fine di isolare l’ambiente contro le previste fonti di rumore esterno.
Coefficienti di riflessione, assorbimento e trasmissione
In generale, quando un’onda sonora investe una parete, si suddivide in tre componenti:
- Onda riflessa
- Onda assorbita
- Onda trasmessa
Indicando con: Ir, Ia e It le intensità sonore delle tre componenti e con Ii quella dell’onda incidente, deve valere la seguente relazione:

Dividendo per Ii entrambi i membri dell’equazione di bilancio (1) si trova:
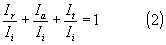
Definendo:
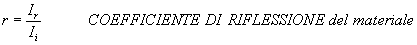


la (2) si può riscrivere:
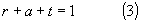
Sino ad ora abbiamo chiamato: COEFFICIENTE DI ASSORBIMENTO ACUSTICO, indicandolo con a
, il rapporto tra l’intensità dell’onda incidente e quella dell’onda NON RIFLESSA dalla parete, ovvero: 
Osserviamo però che a
non è un indice del vero assorbimento acustico da parte dell’ostacolo investito dall’onda sonora, una finestra aperta avrebbe infatti 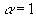 , poiché l’energia riflessa è nulla, ma anche l’energia "assorbita" dalla finestra (nel senso esatto del termine) è nulla, tutta l’energia attraversa infatti l’apertura ed esce dall’edificio! D’ora in poi chiameremo quindi a
: Coefficiente di assorbimento acustico apparente, per distinguerlo da a che è invece il vero e proprio Coefficiente di assorbimento acustico.
, poiché l’energia riflessa è nulla, ma anche l’energia "assorbita" dalla finestra (nel senso esatto del termine) è nulla, tutta l’energia attraversa infatti l’apertura ed esce dall’edificio! D’ora in poi chiameremo quindi a
: Coefficiente di assorbimento acustico apparente, per distinguerlo da a che è invece il vero e proprio Coefficiente di assorbimento acustico.
Quindi l’equazione di bilancio può essere infine scritta come:
 .
.  Fig.1:Rappresentazione grafica della suddivisione di un’onda sonora incidente che colpisce una parete.
Fig.1:Rappresentazione grafica della suddivisione di un’onda sonora incidente che colpisce una parete.
Materiali fonoassorbenti e fonoisolanti
Diciamo fonoassorbente un materiale con elevato coefficiente a
; di solito ciò è dovuto al fatto che una parte dell'energia incidente viene convertita in calore, ma può anche essere dovuto al fatto che viene favorita la trasmissione attraverso il materiale stesso. In modo analogo, diciamo fonoisolante un materiale con basso coefficiente t. Per esempio, una tenda appesa in mezzo a una stanza è altamente fonoassorbente ma poco fonoisolante, perchè l'energia incidente viene in parte convertita in calore per attrito passando attraverso il tessuto ed in gran parte viene trasmessa atraverso la tenda. Un muro massiccio con intonaco liscio è molto fonoisolante ma poco fonoassorbente, perchè quasi tutta l'energia incidente viene riflessa. Il fenomeno è funzione della frequenza. Prima di esaminare più nel dettaglio questi materiali vediamo in quali casi vengono impiegati.
Problemi di disturbo
Esistono essenzialmente due casi di disturbo sonoro:
- Sorgente nella STESSA STANZA del ricevitore
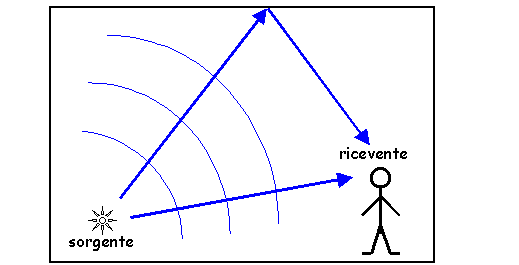
Fig. 2: Il rumore emesso dalla sorgente investe direttamente o indirettamente il ricevitore, che è posto nella medesima stanza.
In tal caso, per abbassare il livello di rumore al ricevitore, si impiegano materiali FONOASSORBENTI, i quali, diminuendo l’intensità dell’onda riflessa, diminuiscono il riverbero sonoro.
- Sorgente e ricevitore in due STANZE DIVERSE
La trasmissione del rumore entro gli edifici presenta una natura duplice: per via aerea (entrando attraverso aperture e fessure, porte o finestre poco ermetiche, prese d’aria e condotti di scarico d’aria), quando il mezzo principale di trasmissione è costituito dall’aria e per via strutturale (attraverso pareti, pavimenti, soffitti, colonne, travi, tubazioni, condotti ed altre strutture solide), in tal caso il rumore può raggiungere punti remoti dell’edificio sotto forma di vibrazioni attraverso le strutture; da queste è poi restituito all’ambiente dove le condizioni risultano più "favorevoli".
Nel primo caso, vedi Fig.3, si cerca di contenere il livello di rumore usando opportuni criteri di progettazione della struttura (ad esempio facendo particolare attenzione agli impianti di areazione) ed impiegando materiali acustici per l’edilizia, stavolta FONOISOLANTI.
Nel secondo caso, vedi Fig.4, si punta, invece, essenzialmente sull’uso di materiali FONOISOLANTI.
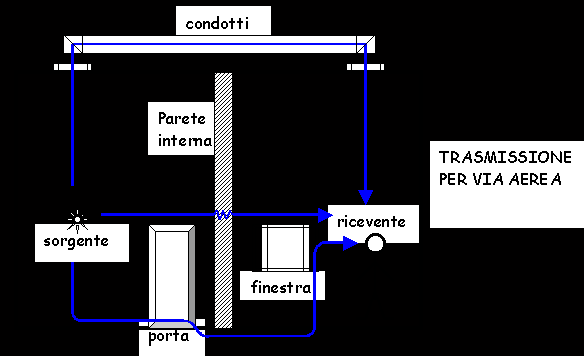 Fig. 3: Il rumore prodotto dalla sorgente viene trasmesso per VIA AEREA e raggiunge il ricevitore in una diversa stanza dell’edificio.
Fig. 3: Il rumore prodotto dalla sorgente viene trasmesso per VIA AEREA e raggiunge il ricevitore in una diversa stanza dell’edificio.
 Fig. 4: Il rumore prodotto dalla sorgente viene trasmesso per VIA STRUTTURALE, ovvero tramite vibrazioni dei corpi elastici, e raggiunge il ricevitore in una diversa stanza dell’edificio.
Fig. 4: Il rumore prodotto dalla sorgente viene trasmesso per VIA STRUTTURALE, ovvero tramite vibrazioni dei corpi elastici, e raggiunge il ricevitore in una diversa stanza dell’edificio.
Materiali porosi
In tali materiali le onde sonore che si producono all’esterno mettono in vibrazione le particelle d’aria entro il materiale. L’attrito delle molecole d’aria con i pori e le fibre del materiale stesso produce la dissipazione dell’energia sonora e la sua trasformazione in calore. In pratica all’interno dei materiali si sviluppa una certa resistenza di flusso nei confronti dell'aria contenuta, in presenza di energia sonora dall’esterno.
È importante chiarire che non è necessariamente l’aria esterna (dell’ambiente) a dover entrare nel materiale affinché si produca l’assorbimento dell’energia sonora. È sufficiente che venga messa in vibrazione quella già contenuta nel materiale. Questo spiega come l’effetto fonoassorbente si produca anche quando il materiale è protetto da un film plastico impermeabile di massa trascurabile (mylar). Il film segue le variazioni della pressione sonora all’esterno e le restituisce all’aria entro il materiale, dove si effettua successivamente la dissipazione dell’energia.
Questi materiali fonoassorbenti si possono dividere in base alla composizione tra materiali a struttura fibrosa (fibre minerali, fibre di vetro, di cellulosa, ecc.) e i materiali plastici espansi (poliuretano). Questi ultimi devono però presentare strutture a celle aperte per risultare efficaci. I materiali con strutture a celle chiuse impediscono il movimento dell’aria al loro interno e non consentono la dissipazione dell’energia sonora da cui sono investiti.
Le prestazioni intrinseche dei materiali vengono influenzate in misura apprezzabile da alcune condizioni per così dire "esterne":
- Spessore del materiale;
- Sistema di applicazione: presenza di un’eventuale intercapedine (e sua profondità) tra il pannello e la parete;
- Sistema di sospensione del pannello alla parete;
- Tipo di rivestimento o protezione superficiale (del pannello).
È utile esaminare singolarmente gli effetti di tali condizioni.
Lo spessore del materiale determina la lunghezza d’onda alla quale avviene il massimo assorbimento dell’energia sonora. In teoria, il massimo assorbimento si verifica per una lunghezza d’onda che è circa quattro volte lo spessore del materiale fonoassorbente messo in opera. Ad esempio, per un tono a 63 Hz (a cui corrisponde una lunghezza d’onda di circa 5,4m), il massimo assorbimento sarà dato da un materiale con spessore teorico di circa 1,35m. Analogamente, per un tono a 4000Hz (lunghezza di circa 0,085m) il massimo assorbimento si otterrà con uno spessore di soli 0,02m. È chiaro dunque che un aumento dello spessore del materiale produce un aumento dell’assorbimento soprattutto alle frequenze al di sotto di 1000Hz.
L’intercapedine d’aria tra il pannello fonoassorbente e la parete di fondo costituisce in pratica un "aumento" dello spessore del pannello medesimo. Ai fini dell’assorbimento delle basse frequenze si considera la profondità totale tra la superficie esterna del pannello e la superficie della parete. Vedi Fig. 5.
La presenza di una intercapedine d’aria può quindi migliorare sensibilmente l’assorbimento alle basse frequenze di uno stesso materiale. Quanto maggiore dunque risulta la profondità complessiva pannello-intercapedine, tanto migliore sarà l’assorbimento alle basse frequenze.
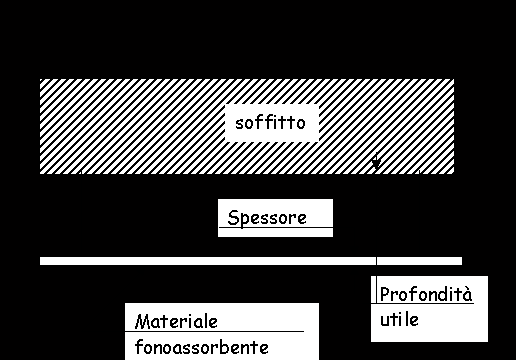
Fig.5: Spessore reale e profondità utile per l’attenuazione dei toni a bassa frequenza da parte di materiali fonoassorbenti.
Il sistema di sospensione del materiale assorbente influenza sensibilmente le prestazioni finali. Pertanto nel confrontare le caratteristiche di assorbimento di materiali diversi è necessario sempre verificare che esse siano riferite alle medesime condizioni di prova.
In pratica esistono tre diversi metodi di applicazioni ai quali si fa riferimento:
- Materiale applicato direttamente sulla parete;
- Materiale montato su travetti distanziatori lasciando un’intercapedine d’aria di 2,5cm rispetto alla parete;
- Materiale sospeso (applicazione a soffitto) lasciando una intercapedine d’aria di 40cm.
I tre sistemi di applicazione sono schematizzati in Fig.6.
Le prestazioni dei tre sistemi, a parità di altre condizioni, si discostano sensibilmente per le frequenze al di sotto dei 500Hz. Esiste una notevole differenza nel coefficiente di assorbimento acustico a favore della soluzione di montaggio (c) rispetto a tutte le altre. Al di sopra dei 1000Hz invece non si producono differenze significative.
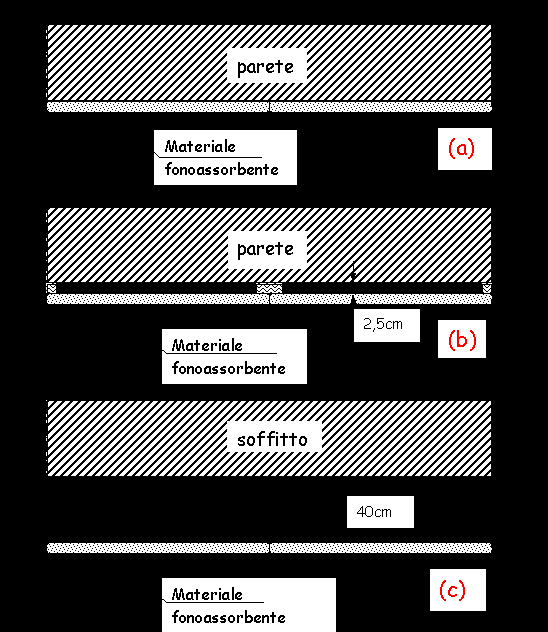
Fig.6- Metodi di applicazione dei materiali fonoassorbenti su pareti e soffitti. Le prestazioni dei materiali vengono generalmente riferite ad uno o più di questi sistemi di montaggio.
(a)
applicazione del materiale a contatto diretto della parete; (b) materiale montato su travetti con profondità di 2,5cm; (c) materiale sospeso a soffitto con intercapedine d’aria di 40cm.
Il tipo di protezione superficiale dei materiali fonoassorbenti costituisce un altro fattore che influenza la resa finale. Raramente è possibile esporre il materiale senza una qualche forma di protezione superficiale, per motivi estetici, di pulizia, igiene e per evitare che depositi di polvere ne alterino nel tempo le caratteristiche. Spesso si applicano lamiere sottili perforate, in acciaio o alluminio, o pannelli in materiale fibroso a bassa densità anch'essi forati.
Il materiale fonoassorbente viene posto dietro il pannello di protezione, ma leggermente staccato dalla superficie, mediante distanziatori. Questi elementi di protezione riducono le caratteristiche di assorbimento acustico alle frequenze superiori a 1000Hz. Infatti, a tali frequenze, i toni presentano ridotte lunghezze d’onda che vengono in buona parte riflesse se incontrano le superfici continue, non perforate, dei pannelli.
Invece, per i toni a bassa frequenza, le corrispondenti elevate lunghezze d’onda subiscono diffrazione da parte delle superfici riflettenti, riescono ad aggirarle e accedono attraverso i fori all’interno del materiale fonoassorbente.
L’uso di superfici perforate di protezione riduce dunque la caratteristica di assorbimento del materiale acustico alle alte frequenze.
Oltre che con pannelli rigidi la protezione superficiale di materiali a struttura fibrosa viene effettuata spesso mediante l’impiego di film plastici, di tessuti in fibra di vetro, ecc. Tali soluzioni sono generalmente utilizzate per i pannelli destinati ai controsoffitti. Questo tipo di protezione non introduce modifiche di rilievo alle caratteristiche del materiale.
Risuonatori assorbenti
È noto che soffiando dell’aria attraverso il collo di una bottiglia vuota si può udire un suono, la bottiglia agisce da risuonatore.
Ci sono prove che suggeriscono che vasi ceramici e giare con aperture in aria furono costruite, sotto i posti a sedere, negli antichi anfiteatri Greci ed in alcune pareti di chiese medievali, per scopi acustici.
Più tardi i risuonatori semplici furono chiamati: RISUONATORI DI HELMHOLTZ, dal nome dello studioso che per primo ne descrisse le caratteristiche.
Tali strutture sono costituite da un volume, contenente aria, connesso alla stanza attraverso un collo ristretto ed un’apertura (vedi Fig.7). L’energia del suono incidente fa vibrare l’aria contenuta nel collo del risuonatore e, a causa del suo volume compresso, si comporta come una massa collegata ad una molla (l’aria nella camera principale). Come per qualsiasi sistema massa-molla, esiste una frequenza di risonanza alla quale si ha la vibrazione massima.
Se la frequenza del suono incidente coincide con quest’ultima, il trasferimento di energia sarà massimo, e quindi anche l’assorbimento, a causa delle perdite per attrito.
I risuonatori di Helmholtz sono particolarmente efficienti solo su uno stretto intervallo di frequenze, normalmente basse (vedi Fig.8).
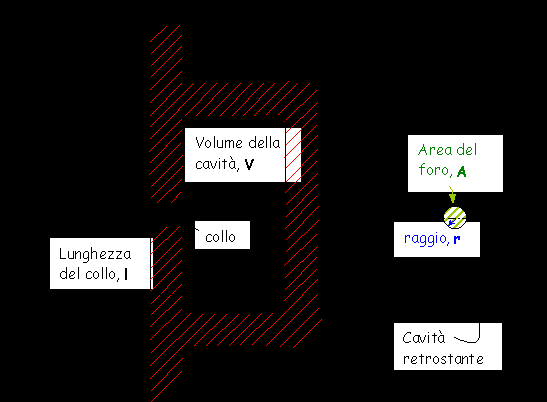
Fig.7: Struttura di un risuonatore di Helmholtz.
La frequenza di risonanza approssimativa, per un risuonatore con apertura circolare, è data da:
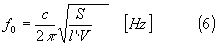
dove:
c = velocità del suono in aria, in 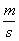
S = area superficiale del collo, in 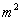
l’ = lunghezza efficace del collo = 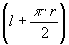 , in m
, in m
r = raggio dell’apertura, in m
V = volume dell’aria contenuta nella camera, in 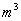 .
.
L’assorbimento massimo di un singolo risuonatore non smorzato dipende dalla sua frequenza di risonanza e può essere stimato con la seguente formula:
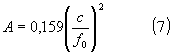
dove:
A = area di assorbimento equivalente totale, in 
c = velocità del suono nell’aria, in 
f0 = frequenza di risonanza, in Hz.
Se è richiesto di allargare la risposta di questo tipo di risuonatore, si può porre un materiale poroso nella cavità risonante, il cui effetto è quello di rallentare per attrito il movimento dell’aria all’interno della cavità stessa, questo aumenterà lo spettro di assorbimento, ma contemporaneamente ridurrà l’efficacia del risuonatore alla frequenza di risonanza (ovvero l’altezza del picco di assorbimento).
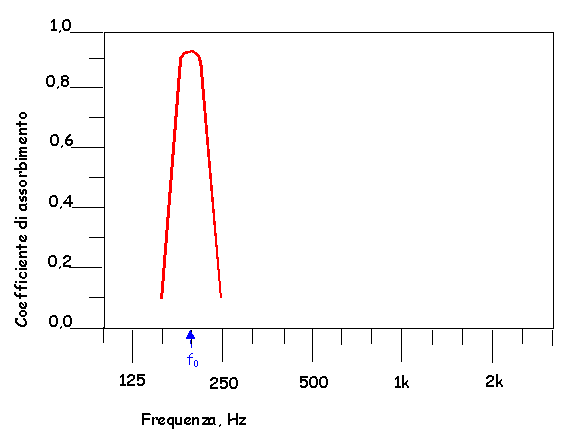
Fig.8: Caratteristica di assorbimento sonoro di un risuonatore di Helmholtz.
Pannelli assorbenti perforati
I risuonatori di Helmholtz sono costosi da realizzare ed efficaci solo su strette bande di frequenza. Un meccanismo simile di assorbimento si ottiene con pannelli perforati, montati ad una certa distanza da una superficie rigida (vedi Fig.9); i fori nel pannello agiscono come una serie di "colli" che dividono la stessa "camera". L’aria contenuta in queste aperture, analogamente al risuonatore di Helmholtz, si comporta come una serie di masse connesse ad un’unica molla (l’aria compresa nello spazio tra il pannello perforato e la superficie rigida posteriore), vi sarà dunque una frequenza di risonanza alla quale l’assorbimento dell’onda sonora è massimo. Come per il risuonatore singolo, è possibile prevedere la frequenza di risonanza di detta struttura mediante la formula empirica:

dove:
c = velocità del suono in aria, in 
P = rapporto di perforazione = 
d = distanza del pannello dalla parete rigida, in m
l’ = lunghezza efficace del collo =  , in m
, in m
r = raggio dei fori, in m.
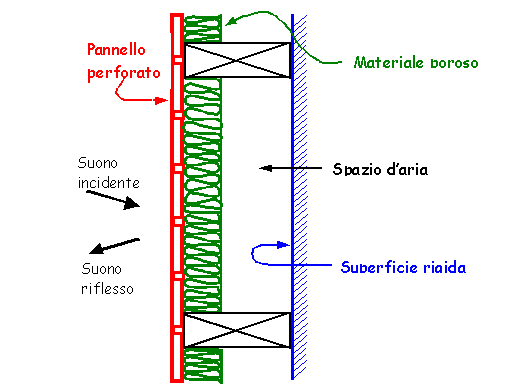
Fig. 9: Struttura di un sistema di isolamento a pannelli perforati assorbenti.
Volendo ottenere un assorbimento più regolarmente distribuito su una banda di frequenze più ampia, occorre praticare dei fori di diverso diametro, ovvero spaziarli disuniformemente in modo da variare il volume della cavità. Quest’ultimo effetto può anche essere ottenuto mantenendo inalterata la foratura e variando lo spazio vuoto dietro il pannello con una delle disposizioni indicate, a titolo di esempio, in Fig.10-(a) e (b).
Normalmente, la cavità tra pannello e parete viene riempita, parzialmente o totalmente, di materiale assorbente, al fine di ottenere un valore opportuno per lo smorzamento.
Nella pratica tali strutture vengono utilizzate nel campo delle medie frequenze, tra circa 500 e 1500Hz.
In Fig.11 è riportata la curva di assorbimento di una struttura costituita da pannelli spessi 10mm, con foratura disuniforme, montati con intercapedine d’aria di 6cm riempita di lana di vetro.
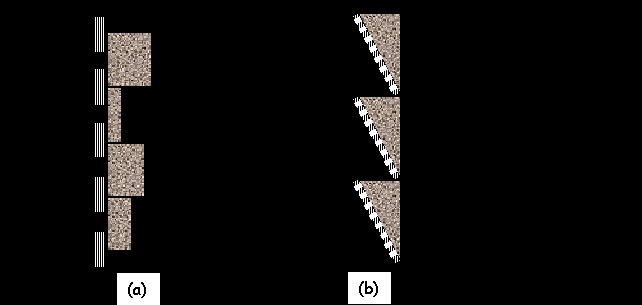 Fig.10-(a) e (b): Disposizione di risuonatori multipli accordati su frequenze diverse.
Fig.10-(a) e (b): Disposizione di risuonatori multipli accordati su frequenze diverse.
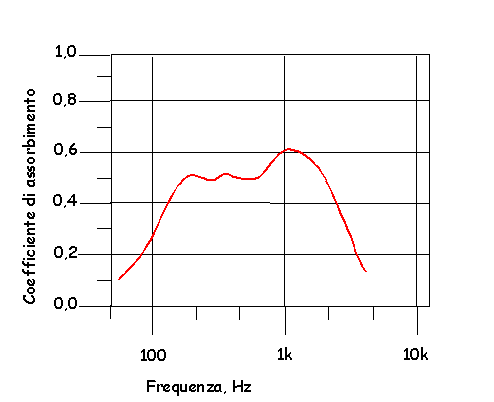
Fig. 11: Curva di assorbimento di pannelli disuniformemente forati.
Pannelli vibranti
Se un materiale ermetico, relativamente sottile, viene fissato ad una certa distanza da una superficie rigida, esso si comporterà come un sistema massa-molla e mostrerà risonanze caratteristiche (frequenze preferenziali di vibrazione).
Quando un’onda sonora colpisce questi pannelli, tenderà a forzare il sistema in vibrazione; se la frequenza del suono incidente corrisponde ad una delle frequenze di risonanza del sistema, il trasferimento di energia che ha luogo è massimo.
Poiché i pannelli sottili hanno un’inerzia e sono inoltre smorzati dal fissaggio alle estremità, parte dell’energia sonora che li investe viene convertita in energia meccanica e quindi "assorbita".
D’altra parte, essendo il pannello stesso posto in vibrazione, esso irradierà nuovamente energia nella stanza, la sua efficienza come materiale fonoassorbente è quindi limitata.
I pannelli assorbenti di uso comune tendono ad essere più efficaci alle basse frequenze, con un picco di assorbimento massimo alla frequenza di risonanza; in generale, all’aumentare della densità superficiale del pannello e/o della profondità dell’intercapedine d’aria tra pannello e superficie rigida, la frequenza di assorbimento massimo diminuisce, essa segue infatti la relazione:

dove:
s
è la densità superficiale del materiale, espressa in 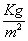 ;
;
d è la profondità dell’intercapedine d’aria.
Se viene richiesto un allargamento dell’intervallo effettivo di frequenze assorbite, è necessario inserire nell’intercapedine d’aria un materiale assorbente poroso.
In Fig.11 e 12 sono mostrate: la struttura di un sistema di isolamento a pannelli vibranti e l’andamento tipico del coefficiente di assorbimento, in funzione della frequenza dell’onda incidente.
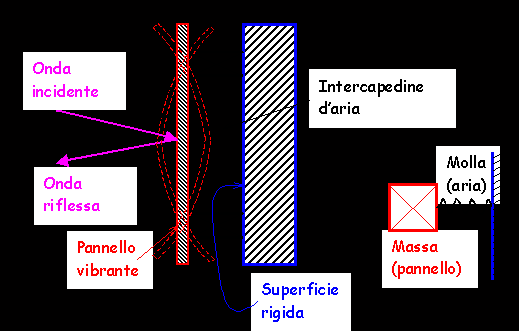 Fig.11: struttura di un pannello vibrante.
Fig.11: struttura di un pannello vibrante.
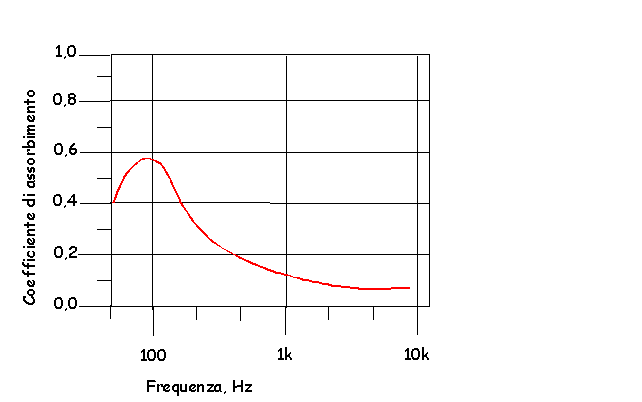
Fig.12: Curva di assorbimento tipica di una struttura a pannello
Per i pannelli aventi dimensioni e peso usualmente adottati nella pratica, la frequenza di risonanza cade entro un intervallo compreso all’incirca tra 50 e 300Hz.
Potere fonoisolante
Consideriamo una parete di un certo spessore e supponiamo che su di essa incida un suono con un livello di intensità pari, ad esempio, a 70dB. Il suono emergente dall’altra faccia della parete avrà, dipendentemente dalla natura e dallo spessore della struttura, un livello relativamente inferiore, supponiamo 40dB. Ciò significa che una parte dell’energia incidente è stata dissipata all’interno della parete. Se ora aumentiamo di 10dB il livello del suono incidente, della stessa quantità aumenterà anche il livello del suono emergente. La differenza tra questi due livelli (suono entrante e suono uscente) è quindi una costante e costituisce una caratteristica della parete. Tale caratteristica viene definita attenuazione di parete o potere fonoisolante R e rappresenta il rapporto, espresso in dB, tra l’energia totale incidente Ii e la frazione di essa che riesce ad attraversare la parete stessa.
Ricordando la definizione di coefficiente di trasmissione, il potere fonoisolante R risulta quindi correlato a t dalla relazione:
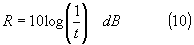
R è direttamente misurabile in una camera riverberante, è comunque opportuno poter prevedere questo valore (prima della messa in opera dei materiali) per la progettazione di un ambiente con caratteristiche acustiche predefinite. Una delle espressioni usate per stimare R è la Legge di massa, ovvero:

Espressione ottenuta mediante passaggi teorici che ben si accorda con i risultati sperimentali.
Come si vede, R risulta proporzionale sia al logaritmo della massa superficiale, sia al logaritmo della frequenza; pertanto, un raddoppio della frequenza o della massa porta ad un aumento di 6dB del potere fonoisolante.
Questo risultato è valido nel caso di onde sonore piane incidenti normalmente sulla parete divisoria. Nella pratica è però maggiormente utile poter prevedere il comportamento di una parete nel caso di suono mediamente diffuso o perfettamente diffuso, questo poiché il suono giunge di norma sulla parete da tutte le direzioni, ossia sotto tutti gli angoli di incidenza. Si impiegano allora altre due relazioni per il calcolo di R, ovvero:
per suono perfettamente diffuso

per suono mediamente diffuso

Tutte le espressioni viste per il calcolo di R valgono per pareti non porose, omogenee ed isotrope.
Deviazioni dalla legge di massa
In accordo con la teoria, l’attenuazione di una parete omogenea dovrebbe aumentare di 6dB per ogni raddoppio della frequenza; tuttavia, da misure sperimentali, si osserva che questo risultato teorico è valido solo entro un certo campo di frequenze intermedie (regione III), come mostrato in Fig.13.

Fig.13: Curva rappresentativa dell’andamento del potere fonoisolante, in funzione della frequenza, per una parete omogenea singola.
Le deviazioni dalla legge di massa, chiaramente visibili nelle regioni (I), (II), (IV) e (V), relative alle frequenze molto basse e molto alte, sono dovute ad effetti particolari, che sono di seguito brevemente illustrati.
Questo effetto si manifesta nel caso di pareti sottili molto rigide e di peso trascurabile. In tali condizioni, il potere fonoisolante segue l’andamento della linea indicata in Fig.13 (regione (I)), ossia cresce al diminuire della frequenza. Tale fenomeno si verifica nel caso delle pareti (o pavimenti) reali per valori della frequenza inferiori ad una frequenza fondamentale naturale f0, compresa normalmente entro l’intervallo 10¸
20Hz. Per tale motivo questo effetto, dal punto di vista dell’attenuazione del suono, non ha importanza pratica.
Si consideri una parete piana incastrata ai bordi, eccitando in un modo qualunque tale parete, essa entra in vibrazione ad una frequenza particolare, detta frequenza fondamentale naturale, che dipende sia dalla massa sia dalla rigidità flessionale della struttura. Gli effetti di queste due grandezze agiscono in direzioni opposte, nel senso che la frequenza fondamentale decresce all’aumentare della massa e cresce al crescere della rigidità flessionale. La frequenza f0 per la quale l’effetto della massa e l’effetto della rigidità flessionale assumono la stessa importanza, annullandosi quindi reciprocamente, rappresenta la frequenza di risonanza.
A parità di ogni altra condizione, la frequenza fondamentale cresce proporzionalmente con lo spessore (rigidità) e inversamente al peso per unità di superficie (massa). La f0 ha generalmente valori compresi tra 1 e 100Hz.
Quando la frequenza del suono incidente è uguale a quella di risonanza della parete, quest’ultima entra in vibrazione con oscillazioni di ampiezza maggiore che alle altre frequenze. In tali condizioni, la parete diventa sostanzialmente trasparente al suono ed il suo potere fonoisolante, di conseguenza, raggiunge un valore minimo. La frequenza f0 rappresenta la prima (e la più importante) di una serie di frequenze proprie di risonanza dovute, come è noto, a ciascuno dei modi naturali di vibrazione di cui è dotata ogni piastra vibrante. In corrispondenza a ciascuna di tali frequenze, fn il potere fonoisolante passa per dei minimi, ossia, come nel caso della frequenza fondamentale, la parete diviene pressoché trasparente al suono. Questa situazione è rappresentata nella regione (II) di Fig.13 dalle successive alternanze che caratterizzano il primo tratto della retta che esprime la legge di massa.
Quest’effetto è mostrato nella zona (IV) di Fig.13; ciò che accade è che in una parete, opportunamente eccitata da un’onda sonora incidente, si formano onde flessionali, la cui velocità non è costante, ma è proporzionale alla radice quadrata della frequenza.
Quando l’onda generata (flessionale) ha velocità pari alla velocità del suono nel particolare materiale che forma la parete, quest’ultima risulta "trasparente" all’onda incidente. Questa situazione è illustrata in Fig.14, in cui i parametri indicati sono tali da verificare la relazione:

Tale fenomeno si verifica ad una particolare frequenza, detta appunto Frequenza di coincidenza fc. Per i materiali impiegati nell’edilizia il valore di fc può variare entro un intervallo assai ampio di valori (da alcune decine ad alcune migliaia di Hz), dipendentemente dallo spessore della parete, dalla natura e dalle caratteristiche del materiale. Tale frequenza può essere calcolata con la relazione:
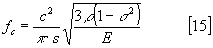
dove:
c = velocità del suono in aria, m/s
r
= densità del materiale, kg/m3
s
2 = coefficiente di Poisson (adimensionale)
E = Modulo di elasticità del materiale (Modulo di Young), N/m2
S = spessore della parete, m
Nell’intorno di questo valore, l’effetto di coincidenza si manifesta con una perdita del potere fonoisolante fino a 15¸
20dB rispetto al valore teorico prevedibile con la legge di massa.

Fig.14: Effetto di coincidenza.
Nella zona (V) è difficile stabilire cosa accade, dipende dal tipo di materiale scelto; tipicamente, per tutto il restante intervallo di frequenze, si osserva che il potere fonoisolante si mantiene circa 5¸
10dB al di sotto del valore previsto dalla legge di massa.
Quanto detto sin ora vale per PARETI OMOGENEE; in caso di pareti formate da materiali diversi e possibile ottenere le stesse prestazioni in termini di potere fonoisolante usando strutture a minore spessore; quindi, a parità di peso, miglioro l’isolamento acustico. Pareti siffatte prendono il nome di PARETI DOPPIE.
Osserviamo infine che anche se l’isolamento delle pareti viene realizzato in modo esemplare, porte e finestre mal progettate nel locale possono invalidarne la funzione; ovvero: gli elementi dal potere fonoisolante della struttura minore condizionano pesantemente il potere isolante complessivo, quest’ultimo è infatti dato da:
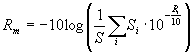
dove:
S = Superficie totale
Si = Superficie i-esima che compone la superficie totale
Ri = Potere fonoisolante della superficie i-esima.
Applichiamo subito questo concetto nel seguente esercizio.
ESERCIZIO
Consideriamo una parete di superficie totale pari a 17m2 (ST); essa è composta per 15m2 (Sd) di materiale omogeneo, di densità r
e spessore d, e per 2m2 (Sf) da una finestra, con potere fonoisolante R.
Determinare il potere fonoisolante globale per un’onda incidente diffusa, alla frequenza di 1kHz.
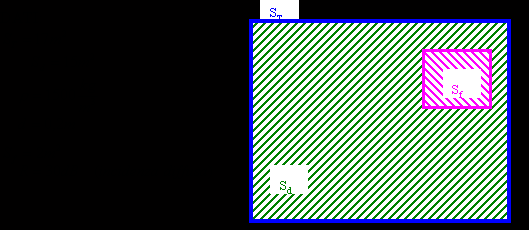
SOLUZIONE:
Calcoliamo il potere fonoisolante della parete: Rd, per determinarlo è necessario calcolare innanzitutto la densità superficiale s
:
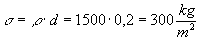
Utilizzando la legge di massa, ipotizzando che non ci siano aperture nella parete, come scatole per gli interruttori elettrici, si ricava direttamente il valore di Rd:
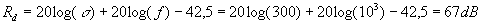
Il potere fonoisolante della finestra: Rf è già un dato del problema e non necessita dunque di calcoli, è quindi possibile calcolare il potere fonoisolante globale come:
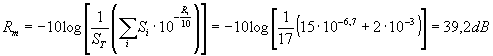
Che è il risultato da noi cercato.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , poiché l’energia riflessa è nulla, ma anche l’energia "assorbita" dalla finestra (nel senso esatto del termine) è nulla, tutta l’energia attraversa infatti l’apertura ed esce dall’edificio! D’ora in poi chiameremo quindi a
: Coefficiente di assorbimento acustico apparente, per distinguerlo da a che è invece il vero e proprio Coefficiente di assorbimento acustico.
, poiché l’energia riflessa è nulla, ma anche l’energia "assorbita" dalla finestra (nel senso esatto del termine) è nulla, tutta l’energia attraversa infatti l’apertura ed esce dall’edificio! D’ora in poi chiameremo quindi a
: Coefficiente di assorbimento acustico apparente, per distinguerlo da a che è invece il vero e proprio Coefficiente di assorbimento acustico.![]() .
.  Fig.1:Rappresentazione grafica della suddivisione di un’onda sonora incidente che colpisce una parete.
Fig.1:Rappresentazione grafica della suddivisione di un’onda sonora incidente che colpisce una parete.
 Fig. 3: Il rumore prodotto dalla sorgente viene trasmesso per VIA AEREA e raggiunge il ricevitore in una diversa stanza dell’edificio.
Fig. 3: Il rumore prodotto dalla sorgente viene trasmesso per VIA AEREA e raggiunge il ricevitore in una diversa stanza dell’edificio. Fig. 4: Il rumore prodotto dalla sorgente viene trasmesso per VIA STRUTTURALE, ovvero tramite vibrazioni dei corpi elastici, e raggiunge il ricevitore in una diversa stanza dell’edificio.
Fig. 4: Il rumore prodotto dalla sorgente viene trasmesso per VIA STRUTTURALE, ovvero tramite vibrazioni dei corpi elastici, e raggiunge il ricevitore in una diversa stanza dell’edificio.


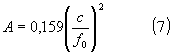



 Fig.10-(a) e (b): Disposizione di risuonatori multipli accordati su frequenze diverse.
Fig.10-(a) e (b): Disposizione di risuonatori multipli accordati su frequenze diverse.
 Fig.11: struttura di un pannello vibrante.
Fig.11: struttura di un pannello vibrante.