FLUIDODINAMICA

La fluidodinamica è quella parte della meccanica che si occupa delle leggi riguardanti il movimento dei fluidi (liquidi ed aeriformi) in relazione sia alle cause che hanno provocato tali movimenti sia agli effetti. La fluidodinamica considera i fluidi come sistemi continui, i quali possono essere compressibili (aeriformi) o incompressibili (liquidi in genere) e classifica il loro movimento in viscoso e non viscoso a seconda delle traiettorie descritte dalle particelle elementari costituenti il sistema.Prima però di addentrarsi nella fluidodinamica è meglio chiarire il concetto di fluido, attraverso una classificazione dei materiali che si evince tramite la prova di compressione.

PROVA DI COMPRESSIONE

La prova di compressione è una prova statica che serve per misurare sperimentalmente il carico di rottura dei vari materiali.

Questa misura si ottiene comprimendo un campione di materiale mediante una pressa; essa imprime al campione in esame una forza di compressione sempre più forte fino a che il materiale si rompe, a questo punto basta leggere sulla pressa la forza applicata al materiale per sapere il suo carico di rottura. Per visualizzare i risultati di questo tipo di prova si utilizzano i cosiddetti diagrammi di carico. Non tutti i materiali hanno lo stesso comportamento nella prova di compressione; si possono distinguere due grandi categorie di materiali:

· Materiali elastici;

· Materiali non elastici;

I materiali elastici hanno la caratteristica di deformarsi sotto l’azione di forze esterne e di riprendere la forma e le dimensioni primitive al cessare delle forze che dette deformazioni hanno provocato. Analogamente i materiali non elastici, sotto l’azione di forze esterne si deformano anch’essi ma al cessare delle forze che hanno provocato la deformazione non ritornano nella forma e nelle dimensioni primitive. In questa analisi si andrà a studiare più da vicino i materiali elastici.

Un materiale elastico ideale, ha la caratteristica di assorbire tutta l’energia fornita nella deformazione del corpo e al cessare delle forze che l’hanno provocata cede l’energia immagazzinata completamente senza dissipazione di energia.

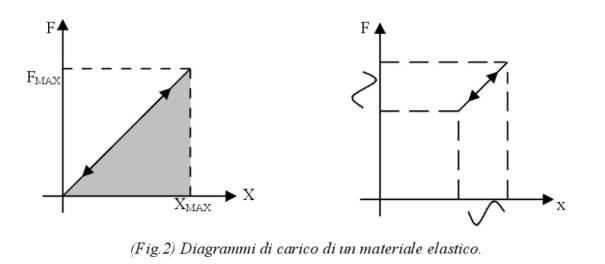
Questi due diagrammi di carico, di un materiale elastico ideale, rappresentano il comportamento del corpo durante la prova di compressione. Il primo diagramma mostra che tutta l’energia fornita al materiale durante la prova di compressione serve per deformare il campione in prova, e che al cessare dell’azione deformante il corpo riprende la forma e le dimensioni primitive, cioè quelle che aveva prima della prova. L’energia ceduta al materiale in esame durante la prova di compressione è data dall’area sottesa dalla curva (F_MAX e X_MAX rappresentano rispettivamente il carico di rottura e la deformazione massima subita da tale sforzo):

(1)

L’energia immagazzinata e spesa è l’area del triangolo.

Il secondo diagramma mostra il comportamento di un campione di materiale, sempre elastico, sotto l’azione di un carico sinusoidale; questo grafico mostra bene la linearità tra forza applicata e deformazione mettendo in evidenza la mancanza di fenomeni dissipativi nei materiali elastici. Vi è un’analogia tra la legge di Ohm che mette in relazione tensione e corrente.

I materiali elastici reali si distanziano dal comportamento ideale perché presentano una dissipazione di energia, questi materiali sono detti viscoelastici.

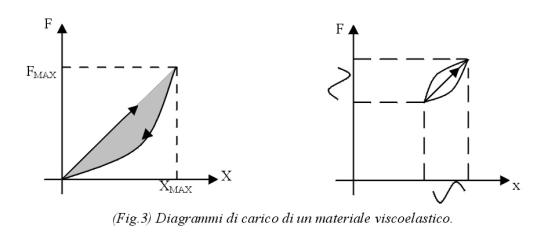
I materiali viscoelastici presentano fenomeni di dissipazione e quindi è opportuno introdurre un coefficiente di dissipazione definito come il rapporto tra l’energia dissipata, cioè l’area sottesa dalla curva di ritorno (l’area colorata di grigio) e l’energia totale fornita al materiale dalla pressa:

(2)

L’energia dissipata è proporzionale alla viscosità del corpo, cioè alla resistenza interna del corpo a lasciarsi deformare. Un materiale può anche non avere un comportamento né strettamente ideale né strettamente viscoelastico per qualsiasi forza applicata.

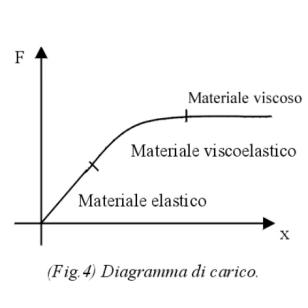
Per sforzi piccoli il materiale si può considerare elastico, infatti si vede linearità tra sforzo applicato e deformazione; per un certo valore di F detto di limite di elasticità, il materiale si può considerare viscoelastico cioè da questo punto in poi il corpo non può più tornare alla forma e alle dimensioni originali (zona di plasticizzazione), per un dato valore di F il materiale diventa un fluido, e se messo in condizioni di scorrere esso procederebbe a velocità costante.

Questo grafico non ha nessuna utilità per lo studio dei fluidi, ma mette bene in evidenza che non vi è alcuna differenza tra un corpo solido ed un fluido, la differenza è solo nella forza che si applica al corpo (Esempio: magma vulcanico).

In conclusione fluido è uno stato della materia in cui le molecole non sono reciprocamente fissate, ma libere di scorrere, quindi la fluidodinamica è quella scienza che studia il comportamento dei materiali che si trovano in questo particolare stato della materia.

INTRODUZIONE

La fluidodinamica può essere suddivisa in due ben distinte categorie a seconda che si studi un fluido che scorre dentro ad un corpo, o se invece un corpo che scorre dentro ad un fluido. Nel primo caso si parla di MOTO INTERNO, nel secondo caso di MOTO ESTERNO.

· Con il termine MOTO INTERNO si indica quella parte della fluidodinamica che studia il moto dei fluidi dentro ad un corpo, come ad esempio all’interno di un condotto. Essa si prefigge di calcolare le cadute di pressione che avvengono tra due sezioni del corpo attraversato dal fluido; tali perdite sono chiamate perdite di carico. La scienza che si occupa di ciò è l’idraulica e studia in particolare il moto dei fluidi incomprimibili cioè che mantengono una densità costante nel loro moto.

· Con il termine MOTO ESTERNO si indica quella parte della fluidodinamica che studia il moto dei fluidi intorno ai corpi, o meglio, studia le forze che i corpi ricevono dai fluidi in movimento, studia in pratica il moto relativo tra fluido e corpo di contatto.

In questa trattazione ci si occuperà solo della parte di fluidodinamica che studia il comportamento dei fluidi dentro ad un corpo, quindi si approfondirà il moto interno.

IPOTESI DI LAVORO

Per semplificare la trattazione matematica del moto di un fluido si dovranno fare varie ipotesi come:

· Ipotesi di incomprimibilità;

· Ipotesi di stazionarietà;

· Ipotesi di aderenza.

1. Nell’ipotesi di incomprimibilità si conviene che il fluido si muova senza modificare la propria densità.

2. Nell’ipotesi di stazionarietà si conviene che il moto del fluido sia stazionario. Per moto stazionario si intende che la velocità in ogni punto del fluido è costante nel tempo, cioè ogni particella che transita per un qualsiasi punto P lo fa sempre con la stessa velocità in modulo e verso.

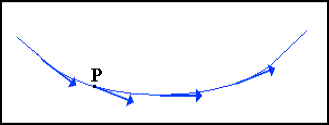
(Fig.5) Linea di flusso. (Fig.6) Tubo di flusso.

Perciò se tracciamo il percorso di una particella, questo sarà anche il percorso di ogni altra particella che arriva in P. La curva che descrive il moto della particella si chiama linea di flusso (fig.5) ed è tangente alla velocità della particella in ogni suo punto. Nel moto stazionario le linee di flusso non si incrociano mai, in quanto se lo facessero una particella che arriva al punto di incrocio potrebbe proseguire lungo una linea o l'altra, quindi in uno stesso punto potrebbe avere differenti valori di velocità, contrariamente all'ipotesi stessa di stazionarietà. È possibile quindi dire che per il moto stazionario esiste una sola linea di flusso per ogni punto del fluido e che l'insieme delle linee di flusso è fisso nel tempo. Prendendo un fascio di linee di flusso otteniamo una superficie tubolare detta tubo di flusso (fig.6).

Per semplicità d'ora in avanti faremo coincidere il tubo di flusso con il condotto reale entro il quale scorre il fluido, ma teniamo presente la natura vettoriale del fluido un moto. Per l'ipotesi di incomprimibilità del fluido osserviamo che il volume del fluido che in un certo tempo attraversa la sezione del condotto non varia con la sezione, altrimenti si avrebbe accumulo o rarefazione di fluido in alcune regioni nelle quali la densità aumenterebbe o diminuirebbe in contraddizione con l'ipotesi di incomprimibilità.

3. Nell’ipotesi di aderenza si conviene che il fluido a contatto con un condotto aderisca alla parete di questo.

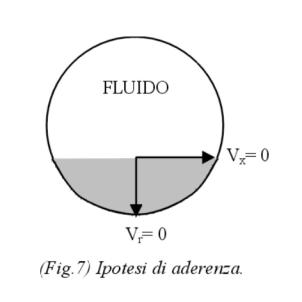
Questa ipotesi, in pratica, esprime il fatto che il fluido che si trova a contatto con la superficie del condotto, aderisca perfettamente ad esso e di conseguenza la sua velocità è nulla.

La velocità del fluido a contatto con il condotto ha due componenti: una tangenziale v_x che si è posta uguale a zero per l’ipotesi di aderenza ed una componente radiale v_r che è chiaramente nulla (il fluido non esce radialmente dal condotto) (fig.7).

Introducendo tutte queste ipotesi, in realtà delle semplificazioni, è chiaro che si studierà qualcosa che non sarà più un fluido reale. Si considereranno però, a favore di una trattazione più completa possibile, fluidi viscosi, cioè fluidi che hanno una resistenza di scorrimento.

VISCOSITÀ

Le grandezze fisiche, viscosità e densità, di un fluido vengono spesso accomunate da uno stesso significato anche se sono due proprietà completamente differenti.

La densità infatti è definita come rapporto tra la massa di un corpo ed il suo volume, mentre la viscosità è l’attrito interno di un corpo.

La viscosità rappresenta la resistenza che le particelle d’un corpo incontrano nello scorrere le une rispetto alle altre, detta anche attrito interno, si manifesta con l’insorgere, nello scorrimento d’uno strato rispetto all’altro, di tensioni tangenziali più o meno elevate a seconda della natura del corpo. La viscosità è molto grande nei solidi elastici e anelastici, molto più piccola nei liquidi viscosi, ma non trascurabile, è praticamente nulla nei liquidi molto scorrevoli e nei gas.

In un fluido che scorre dentro ad un condotto la viscosità può anche essere espressa come l’insieme delle forze tangenziali tra la superficie del condotto ed il fluido e tra strati di fluido diversi che si oppongono al moto del fluido stesso rispetto alla superficie. Queste forze tangenziali sono dette tensioni t e sono della forma:

(3)

dove F è la forza che agisce su un elemento di area A che si oppone al verso del movimento del fluido.

La viscosità nei liquidi deriva dalle forze di coesione intermolecolari; all’aumentare della temperatura, la viscosità diminuisce poiché l’aumento dell’energia cinetica delle molecole riduce l’effetto delle forze intermolecolari. Invece nei gas la viscosità aumenta con la temperatura perché le molecole stesse si spostano tra strati adiacenti e, al crescere della temperatura, aumenta il moto molecolare e quindi lo scambio di molecole tra gli strati. Si osservi, tuttavia, che in una conduttura c’è sempre un numero maggiore di molecole lente vicino alle pareti che non di molecole veloci sull’asse centrale; pertanto lo scambio tra gli strati aumenta quando aumenta il numero di molecole lente che si sposta verso l’asse impedendo il moto di quelle più veloci (l’effetto è analogo a quello di un flusso di traffico lento che si inserisce nella corsia veloce di un’autostrada).

Prendiamo un fluido confinato tra due lastre parallele di area A e distanti tra loro z. Teniamo ferma la lastra inferiore e facciamo scorrere quella superiore con una velocità costante v applicandovi una forza F.

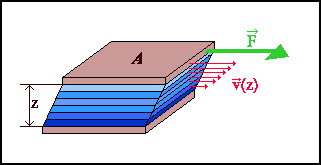
(Fig.8) Flusso viscoso tra 2 piani posti a distanza z.

La velocità degli strati di fluido di spessore infinitesimo decresce uniformemente dal piano superiore a quello inferiore. Tale forza è necessaria perché il fluido vicino alla lastra superiore esercita su essa una resistenza viscosa che si oppone al moto : ogni strato di fluido esercita su quelli adiacenti ad esso una forza resistente dimodoché la velocità del fluido vicino alla lastra alla quale è applicata la forza è v mentre è quasi nulla vicino alla lastra inferiore, variando linearmente con la quota. Il modulo della forza risulta direttamente proporzionale a v e ad A ed inversamente proporzionale alla distanza z tra le lastre attraverso un coefficiente di proporzionalità detto coefficiente di viscosità:

(4)

m è detto coefficiente di viscosità dinamico.

Per riuscire a determinare il coefficiente di viscosità dinamico si può utilizzare il viscosimetro rotazionale.

VISCOSIMETRO ROTAZIONALE

Il viscosimetro è uno strumento per misurare il coefficiente di viscosità dinamica di un fluido. Il viscosimetro rotazionale o di Couette è basato sulla determinazione del momento torcente trasmesso da un corpo posto in rotazione all’interno di un fluido.

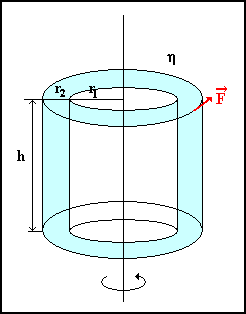
(Fig.9) Viscosimetro rotazionale.

Nel viscosimetro a cilindri coassiali o di Searle (fig.9) un recipiente cilindrico “a”, contenuto in un altro cilindro “b”, è trascinato in rotazione per mezzo di una coppia motore M1. Si misura la velocità angolare del cilindro “b”, il cui valore dipende dal momento resistente offerto dalle tensioni tangenziali di attrito trasmesse dal fluido, contenuto nell’intercapedine dei due cilindri, il liquido è ad un livello A. Si aggiunge liquido fino ad un livello B e si misura la coppia M2 che occorre applicare per avere lo stesso valore della velocità angolare. Il coefficiente di viscosità dinamico risulterà proporzionale alla differenza di coppia M2 – M1.

Ponendo M = M2 – M1 si può scrivere l’equazione di equilibrio delle forze in gioco in questo dispositivo:

(5)

Dove t è la tensione tangenziale riferita all’unità di superficie, 2p×r₁×h è la superficie laterale del cilindro posto in rotazione.

Sapendo che la velocità angolare di rotazione del cilindro è data da:

(6)

Dove RPM è il numero di giri al minuto dell’albero motore.

La velocità tangenziale è definita dalla relazione:

(7)

Dove r₁ è il raggio del cilindro interno.

Ora sapendo che:

(8)

Nel caso specifico del viscosimetro: (9)

In conclusione trovo il coefficiente di viscosità dinamico con la formula:

(10)

LEGGE DI NEWTON

La legge di Newton sancisce la proporzionalità lineare tra la tensione superficiale t e la derivata parziale della velocità del fluido rispetto alla distanza z, e viene espressa con la seguente uguaglianza:

(11)

Il segno meno indica che lo sforzo tangenziale è frenante nel senso che il fluido vede che è la parete che frena il moto del fluido.

Lo sforzo e la derivata della velocità sono legati in modo proporzionale tramite una variabile m dipendente dal tipo di fluido e dalla temperatura. Questa variabile,sino a poco tempo fa, era chiamata coefficiente di viscosità, ed ha le dimensioni di [Pa]·[s]. Oggi le nuove convenzioni impongono che il termine “coefficiente” possa essere attribuito solo a variabili adimensionali, quindi si è dovuto rinominare m come viscosità dinamica.

I fluidi che obbediscono alla legge di Newton sono detti fluidi Newtoniani, ed alcuni di essi sono:

· Acqua;

· Aria;

· Olio d’oliva;

· Olio motori;

· ...

Oltre ad una viscosità dinamica esiste anche una viscosità detta cinematica n che è definita come:

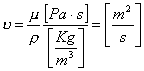(12)

dove r indica la densità del fluido.

Eseguendo una verifica adimensionale:

(13)

Il coefficiente di viscosità dinamico, caratteristico per ogni fluido, determina la pendenza della retta.

Si riporta di seguito alcuni valori dei coefficienti di viscosità di alcuni materiali in funzione della temperatura:

	m (m×Pa×s)	Temperatura (°C)
Acqua	1,79	0
	1,00	20
	0,28	100
Alcool etilico	1,20	20
Glicerina	1490	20
Mercurio	1,685	0
	1,554	20
	1,240	100
Olio d’oliva	84,0	20
Olio per motori	200	30
Sangue	4,0	37

	Viscosità (mP)	Temperatura (°C)
Aria	170,8	0
	182,7	18
Argon	209,6	0
	221,7	20
	269,5	100
Elio	186,0	0
	194,1	20
	228,1	100
Idrogeno	83,5	0
	87,6	20,7
Metano	102,6	0
	108,7	20
	133,1	100
Neon	297,3	0
	311,1	20
	364,6	100
Ossigeno	189	0
	201,8	19,1
	256,8	127,7

Si riportano di seguito le caratteristiche di viscosità e densità dell’aria secca alla pressione di 1 atm:

Temperatura [°C]	Densità [Kg/m^3]	Viscosità dinamica m×10^-6 [N×s/m^2]	Viscosità cinematica n×10^-6 [m^2/s]
-180	3,720	6,472	1,75
-150	2,780	8,591	3,14
-100	1,948	11,866	5,96
-50	1,534	14,808	9,65
-20	1,365	16,279	12,00
0	1,252	17,456	13,90
10	1,206	17,848	14,66
20	1,164	18,240	15,70
30	1,127	18,682	16,58
40	1,092	19,123	17,60
50	1,057	19,515	18,58
60	1,025	19,907	19,40
70	0,996	20,398	20,65
80	0,968	20,790	21,50
90	0,942	21,231	22,82
100	0,916	21,673	23,60
120	0,870	22,555	25,90
140	0,827	23,340	28,20
150	0,810	23,732	29,40
160	0,789	24,124	30,60
180	0,755	24,909	33,00
200	0,723	25,693	35,50
250	0,653	27,557	42,20
300	0,596	29,322	49,20

t

Come si può notare da queste tabelle i coefficienti di viscosità sia dei liquidi che dei gas sono fortemente dipendenti dalla temperatura.

PARABOLA DI POISEUILLE

Per un fluido che imbocca un condotto provenendo da un grande serbatoio, il profilo di velocità, inizialmente piatto o quasi, si deforma via via fino ad assumere la configurazione detta parabola di Poiseuille.

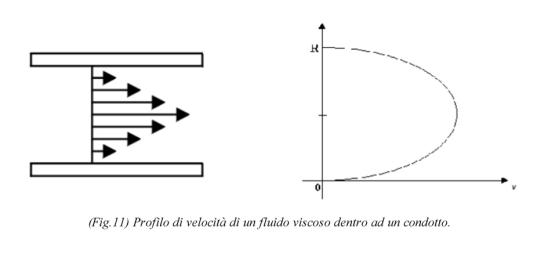
Al rallentamento del fluido all’interno dello strato limite, corrisponde un’accelerazione di quello che si trova fuori, dovendo essere garantita la continuità di portata. Per continuità di portata si intende che la portata in tutte le sezioni di un tubo sia costante.

Si ricorda che per portata in fluidodinamica si intende la quantità di fluido che passa attraverso una generica sezione di tubo nell’unità di tempo. Si può allora, alla luce di queste considerazioni, definire la velocità media W del moto del fluido dentro al condotto, così definita:

(14)

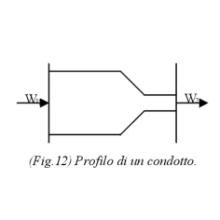
Per un condotto che ha la seguente geometria, si capisce che W₂ > W₁.

Nelle ipotesi di lavoro, si è detto che in questa analisi si studia solo il moto di fluidi detti incomprimibili, cioè aventi densità costante per tutto il loro moto, quindi la portata in volume si può utilizzare senza problemi.

Se si abbandonasse l’ipotesi di incomprimibilità, il fluido cambierebbe densità durante il suo moto (ad esempio quando un condotto si restringe, e dentro ad esso scorre un gas, questo restringimento provoca un abbassamento di pressione e quindi una diminuzione di densità del gas), quindi non sarebbe più utile usare la portata in volume ma sarebbe più informativo utilizzare la portata di massa per definire la velocità media W:

(15)

Utilizzando la portata di massa posso sapere la velocità di un fluido comprimibile in ogni sezione del condotto. Dato che la continuità di portata è verificata, è chiaro che se il fluido è viscoso e se vale l’ipotesi di aderenza, al rallentamento di uno strato di fluido ne consegue che un altro strato deve accelerare.

La parabola di Poiseuille rappresenta il profilo di velocità di un fluido viscoso che scorre dentro ad un condotto, e si nota chiaramente che la velocità di flusso varia con il raggio: sull’asse del tubo si ha il valore massimo, mentre il minimo si ha sulle pareti (che si pone uguale a zero per ipotesi di aderenza). Bisogna notare che il moto di un fluido viscoso dentro ad un condotto è rotazionale, anche se gli elementi di fluido percorrono tratti rettilinei. Infatti un moto si dice rotazionale se nel fluido in moto può esistere un elemento in rotazione attorno ad un asse passante per il centro di massa dell’elemento stesso (ad esempio immaginando una piccola girandola con palette immersa nel fluido in moto se essa ruota su se stessa il moto del fluido è rotazionale).

Nel profilo di velocità del fluido viscoso in moto, si nota che se pongo una piccola girandola in una qualsiasi posizione del moto che non stia sulla linea di corrente centrale, a causa della differente velocità delle particelle di fluido che urtano le sue pale si osserva una rotazione.

Ora si ricaverà un’espressione analitica che descrive il profilo di velocità di un fluido che scorre dentro ad un condotto, cioè si ricaverà l’equazione della parabola di Poiseuille.

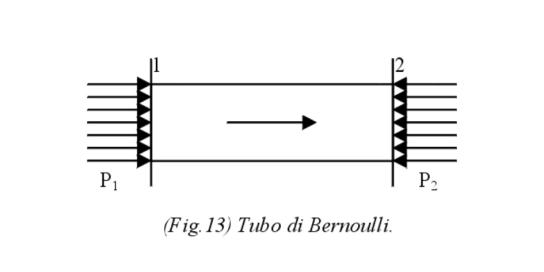
Se il fluido scorre dalla sezione 1 verso la sezione 2, questo significa che: P₁>P₂

Per trovare l’espressione analitica della parabola di Poiseuille pongo le seguenti ipotesi:

· Sistema stabilizzato;

· Moto laminare non turbolento;

· Regime stazionario rispetto a spazio e tempo;

· Fluido viscoso Newtoniano e incomprimibile;

· Forza peso trascurabile.

Prendiamo dunque un tubo liscio a sezione circolare con raggio R, in cui scorre del fluido con velocità v un elemento di volume del fluido di lunghezza L e raggio r, centrato rispetto al piano di simmetria del condotto. Si vuole determinare la perdita di pressione (o di carico) di fluido dovuta a fenomeni di tipo viscoso. Tale perdita di pressione è infatti causata dalle tensioni tangenziali che frenano il fluido in movimento, oppure, equivalentemente, se mi pongo in un punto di vista solidale con il fluido, è dovuta alle tensioni tangenziali scaricate dal fluido stesso sulle pareti del condotto in modo da trascinarlo nel suo moto.

Il bilancio delle forze, che deve essere nullo, si compone di 3 contributi: la pressione P₁ che agisce sulla faccia d’entrata, la contropressione P₂ sulla faccia d’uscita e la forza tangenziale t che frena il fluido in movimento.

Considerando positiva la direzione che va da sinistra verso destra, si ha che P₁ è positivo, mentre i contributi P₂, e t sono negativi. L’equazione di bilancio delle forze diventa quindi:

(16)

Dove 2pRL è l’area laterale del tubo cilindrico e pR² è l’area della sezione del tubo.

Se considero un cilindretto di raggio r < R l’equazione diventa:

(17)

Ricordando la legge di Newton:

(18)

allora l’equazione si può riscrivere:

(19)

Ovvero, facendo le opportune semplificazioni, si ha che:

(20)

Integrando ora questa equazione differenziale a variabili separabili considerando l’ipotesi di aderenza:

(21)

Svolgendo i calcoli:

(22)

Si può ora ottenere un’espressione analitica del profilo di velocità del moto di un fluido viscoso che scorre in un condotto, ossia l’equazione della Parabola di Poiseuille:

(23)

Si può allora calcolare la velocità media W:

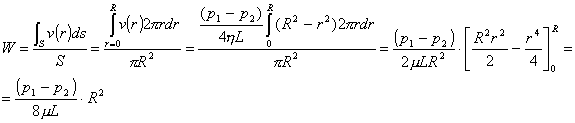(24)

Questa è un’equazione che lega la velocità media con la viscosità del fluido, con la differenza di pressione tra le due sezioni del tubo, e il raggio del condotto. Questa è una relazione che viene utilizzata per dimensionare il circuito; data la viscosità del fluido in moto, il raggio del condotto e sapendo a che velocità si vuole far scorrere il fluido si può ricavare la differenza di pressione da applicare al circuito idraulico per ottenere la velocità di scorrimento desiderata.

Ricavando la formula inversa:

(25)

Con questa espressione posso ricavare le perdite di pressione per attrito in regime laminare; sapendo la velocità media del fluido e la sua viscosità e sapendo le dimensioni del condotto, posso ricavare la perdita di pressione per attrito.

N.B. Tutti questi risultati e considerazioni valgono solo sotto le ipotesi di lavoro che si sono fatte all’inizio del paragrafo.

EQUAZIONE DI BERNOULLI

Le equazioni indispensabili per descrivere il moto dei fluidi, sono:

· La conservazione della portata;

· La conservazione dell’energia.

La conservazione dell’energia di un sistema idraulico si ricava dal bilancio dell’energia dei sistemi aperti:

(26)

Questo termine rappresenta la differenza di energia cinetica tra due sezioni del condotto;

Questo termine rappresenta la differenza di energia potenziale tra due sezioni del condotto;

Questo termine rappresenta la differenza di entalpia tra due sezioni del condotto;

q: Questo termine rappresenta il calore scambiato dal sistema;

l: Questo termine rappresenta il lavoro scambiato dal sistema.

Per il sistema idraulico in questione si può semplificare questa relazione facendo alcune semplici considerazioni; se si considerano fluidi isotermici si può trascurare il termine del calore q.

Sapendo che:

(27)

Dove u è l’energia interna che dipende solamente dalla temperatura, ma se si sono considerati, per ipotesi, fluidi isotermici, allora u(T) = costante, di conseguenza la differenza di entalpia si può ridurre:

(28)

In teoria invece della differenza p₂v₂ – p₁v₁ sarebbe più corretto integrare dato che il prodotto p×v non è una funzione di stato, quindi cambia a seconda del cammino scelto, però per una prima approssimazione e per comodità nei calcoli si accetta la semplificazione eseguita.

Dato che il fluido è incomprimibile, questo significa che non cambia la sua densità durante il moto, quindi r₁ = r₂, l’equazione del bilancio energetico si può riscrivere nel seguente modo:

(29)

È possibile porre l’equazione in un’altra forma, nella quale compaia esplicitamente l’energia meccanica dissipata in conseguenza delle resistenze passive. Sia R l’energia meccanica dissipata per resistenze passive, o perdite di carico:

(30)

Il termine R ha le dimensioni [J/Kg].

Ora che si è analizzato in generale il bilancio energetico di un sistema idrodinamico, si analizza ora un caso particolare di sistema aperto fluidodinamico, la pompa.

Nel caso della pompa l’equazione del bilancio energetico può essere ulteriormente semplificata; infatti la pompa avente sezione d’ingresso uguale alla sezione d’uscita, quindi la velocità w₁ è uguale a w₂ ; il contributo della variazione dell’energia cinetica si annulla.

L’energia potenziale è trascurabile come la dissipazione meccanica R;

l’equazione si riduce:

(31)

Nella pompa la differenza di pressione Dp è detta prevalenza, ed indica l’aumento di pressione della sezione d’uscita 2 rispetto alla pressione della sezione d’ingresso.

(32)

Con questa relazione si vede bene come la prevalenza è legata con il lavoro della pompa. À parità di prevalenza una pompa svolge meno lavoro se il fluido è più denso.

Viscosità dinamica dei principali gas e liquidi in funzione della temperatura:

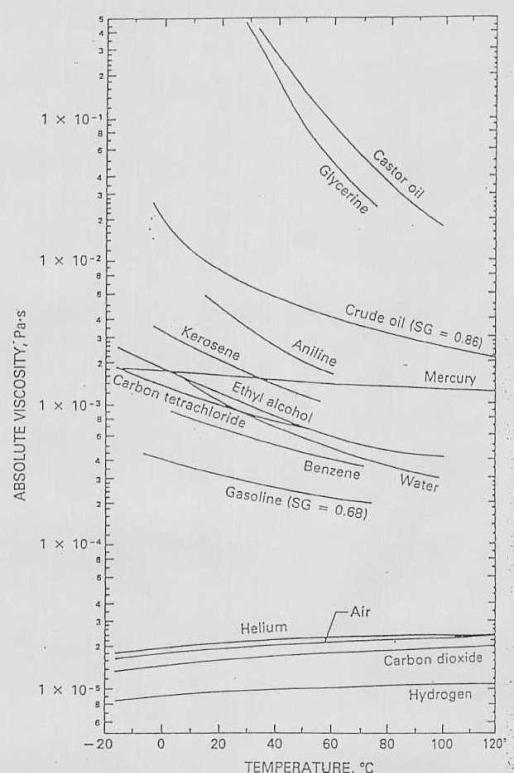
Viscosità cinematica dei principali gas e liquidi in funzione della temperatura: