Applicazioni di scambio termico per irraggiamento
UNIVERSITA’ DEGLI STUDI DI PARMA
Anno accademico 2000-2001
Corso di laurea : ingegneria delle telecomunicazioni
Corso di fisica tecnica
Docente del corso : Angelo Farina
Relazione della lezione di fisica tecnica tenuta il giorno 11/12/2001 alle ore 16 :30-18 :30
Affrontiamo ora una serie di casi pratici legati allo scambio termico per irraggiamento.
In termini di applicazioni noi abbiamo a che fare con scambio termico per irraggiamento quando abbiamo dei corpi nel vuoto. Inizialmente considereremo dei problemi particolarmente semplici perché sono problemi di scambio termico nel vuoto.
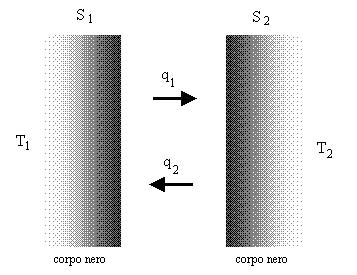
Il caso più semplice che possiamo studiare è quello di superfici piane affacciate e indefinite.
Abbiamo le superfici ![]() e
e ![]() che si trovano a temperatura
che si trovano a temperatura ![]() e
e ![]() e in mezzo abbiamo il vuoto, quindi queste due superfici si scambiano calore perché la superficie di sinistra,
e in mezzo abbiamo il vuoto, quindi queste due superfici si scambiano calore perché la superficie di sinistra, ![]() , emette una quantità di calore, che possiamo chiamare
, emette una quantità di calore, che possiamo chiamare ![]() , e la superficie di destra,
, e la superficie di destra, ![]() , emette una quantità di calore che possiamo chiamare
, emette una quantità di calore che possiamo chiamare ![]() .
.
1° CASO
Il primo caso che andiamo a considerare è quello di due superfici perfettamente nere
Ciascuna delle due emette secondo la legge di Stefan-Boltzmann delle quantità di calore pari a:
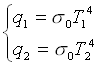
Per la relazione di Prevost la potenza scambiata, ad esempio dalla superficie ![]() , è la potenza emessa meno la potenza incidente, ma la potenza incidente è
, è la potenza emessa meno la potenza incidente, ma la potenza incidente è ![]() perché entrambi i corpi sono neri quindi non c’è potenza riflessa, cioè
perché entrambi i corpi sono neri quindi non c’è potenza riflessa, cioè
a (coefficiente di assorbimento) è pari a 1 oppure r (coefficiente di riflessione) è pari a zero.
Allora la potenza scambiata, per la superficie ![]() , risulta:
, risulta:
![]()
2° CASO
Nel secondo caso supponiamo che una delle due superficie sia grigia lasciando l’altra nera. Ad esempio prendiamo grigia la superficie di sinistra.

Ora la superficie ![]() emette una nuova quantità
emette una nuova quantità ![]() che sarà:
che sarà:
![]()
mentre la superficie ![]() emette sempre la stessa quantità
emette sempre la stessa quantità ![]() del caso precedente però adesso questa quantità
del caso precedente però adesso questa quantità ![]() in parte viene riflessa, cioè esiste una quantità riflessa, che possiamo chiamare
in parte viene riflessa, cioè esiste una quantità riflessa, che possiamo chiamare ![]() . La quantità
. La quantità ![]() non rimbalza infinite volte perché quando torna su
non rimbalza infinite volte perché quando torna su ![]() , che è nera, viene assorbita totalmente.
, che è nera, viene assorbita totalmente.
Dal punto di vista di quello che accade sulla superficie ![]() la quantità che viene riflessa indietro non ha alcun effetto pratico, infatti la superficie
la quantità che viene riflessa indietro non ha alcun effetto pratico, infatti la superficie ![]() emette sempre la quantità
emette sempre la quantità ![]() e riceve sempre la quantità
e riceve sempre la quantità ![]() ; vale ancora la relazione di Prevost, ma non è più vero che il coefficiente di riflessione a vale zero, ma abbiamo che la potenza scambiata è quella emessa meno quella ricevuta
; vale ancora la relazione di Prevost, ma non è più vero che il coefficiente di riflessione a vale zero, ma abbiamo che la potenza scambiata è quella emessa meno quella ricevuta
![]()
3° CASO
L’ultimo caso che andiamo ad analizzare è quello in cui entrambe le superfici sono grigie; la prima è caratterizzata dal coefficiente di assorbimento ![]() e la seconda è caratterizzata dal coefficiente di assorbimento
e la seconda è caratterizzata dal coefficiente di assorbimento ![]() .
.

A questo punto i fenomeni di riflessione diventano più complessi perché la quota di energia che viene riflessa dalla superficie ![]() ritorna sulla superficie
ritorna sulla superficie ![]() e in parte viene riflessa ancora e si avrebbe una serie infinita di rimbalzi sempre più deboli.
e in parte viene riflessa ancora e si avrebbe una serie infinita di rimbalzi sempre più deboli.
Possiamo risolvere questo problema definendo come quantità ![]() non solamente quella riflessa al primo rimbalzo, ma la quantità complessiva che vedo tornare sulla superficie
non solamente quella riflessa al primo rimbalzo, ma la quantità complessiva che vedo tornare sulla superficie ![]() .
.
Analogamente sulla superficie ![]() vedrò cadere non solo la quantità
vedrò cadere non solo la quantità ![]() emessa dalla superficie
emessa dalla superficie ![]() , ma vedrò cadere una quantità
, ma vedrò cadere una quantità ![]() complessiva che è la somma di quella emessa più tutta quella riflessa.
complessiva che è la somma di quella emessa più tutta quella riflessa.

Notiamo che ciascuna relazione richiama l’altra. Queste due equazioni messe insieme costituiscono un sistema lineare di due equazioni in due incognite; sistema che una volta risolto consente di esplicitare i valori delle quantità di calore che piove su ciascuna superficie ![]() e
e ![]() .
.
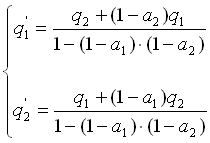
A questo punto scrivendo la relazione di Prevost, che dà la potenza scambiata, ottengo, sempre scrivendo la relazione per la superficie ![]() , otteniamo:
, otteniamo:
![]()
quindi andando a sostituire al posto di ![]() l’espressione trovata e al posto di
l’espressione trovata e al posto di ![]() e
e ![]() le espressioni delle emissioni cioè
le espressioni delle emissioni cioè
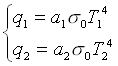
si ottiene l’espressione finale
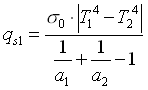 (1.1)
(1.1)
che è l’espressione generale che dà lo scambio termico tra due superfici grigie piane affacciate e indefinite.
Quando è un caso molto comune nella pratica, ad esempio, in campo edile dove è abbastanza comune all’interno della facciata di un edificio (facciata ventilata) avere un muro di mattoni e l’intonaco che arriva ad un certo spessore, ad esempio 25 cm, e lasciare una intercapedine d’aria ed ad una certa distanza montare delle lastre di rivestimento in modo che l’aria resti libera di muoversi.

Quando poi si calcola la resistenza termica complessiva della parete non si può trascurare la potenza scambiata per irraggiamento tra queste due superficie grigie, che si guardano a breve distanza, realizzate con materiali diversi, quindi in generale con coefficiente di assorbimento diversi.
Se l’aria dentro è libera di girare ci saranno anche effetti convettivi che si sovrappongono allo scambio termico irraggiante. Se l’aria è intrappolata e non può circolare allora lo scambio termico per convezione tende a diventare molto più basso e la gran parte di calore è trasferito effetivamente per irraggiamento.
Vediamo un esercizio con due superfici piane e parallele per avere un’idea di quali possano essere le intensità di questi flussi.
ESERCIZIO
Supponiamo di avere due superfici ![]() e
e ![]() rispettivamente a queste temperature:
rispettivamente a queste temperature: 
e i coefficienti di assorbimento dei corpi grigi sono:
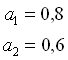
Troviamo ora la potenza scambiata per irraggiamento tra le due superfici.
Utilizzando la formula generale (1.1) otteniamo:
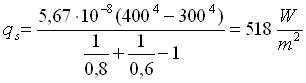
Se poi c’è anche scambio termico per convezione possiamo andare a valutare quanto vale il flusso convettivo utilizzando le relazioni che riguardano tale flusso cioè utilizzando questa relazione:
![]()
per calcolare la potenza occorre il coefficiente di convezione.
Cominciamo a calcolare Nu.
Stiamo trattando un caso di convezione naturale, quindi la formula da utilizzare è la seguente:
![]() (1.2)
(1.2)
La lunghezza caratteristica in caso di superfici affacciate coincide con la distanza tra le due lastre, che supponiamo sia:
![]() cm
cm
quindi vado a calcolare il numero di Grashof:
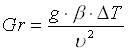
con
b
= inverso della temperatura mediau
= viscosità dell’aria.Andando a sostituire i valori corrispondenti otteniamo il valore

quindi il moto è laminare infatti
![]()
allora le costanti da utilizzare nella formula (1.2) sono:
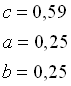
Il numero di Nusselt risulta:
![]()
Possiamo ora calcolare il coefficiente di convezione
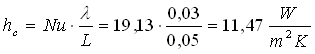
quindi la potenza scambiata per convezione è

notiamo che è due volte la potenza scambiata per irraggiamento, quindi la potenza convettiva in questo caso predomina.
Vediamo cosa succede se alziamo di 200 gradi le temperature, cioè

la differenza è sempre di 100 gradi quindi la potenza convettiva varia di poco in quanto nello scambio termico per convezione non conta il valore assoluto delle temperature ma solo la differenza, mentre nell’irraggiamento è il valore assoluto che conta.
Ripetiamo i calcoli con la variazione delle temperature indicate sopra.
Utilizziamo ancora la formula generale (1.1) per la potenza scambiata per irraggiamento:
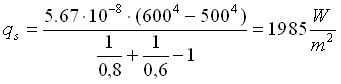
che vediamo comincia ad aumentare in maniera significativa.
Si può notare che varia, anche se debolmente, il numero di Grashof con la temperatura e quindi anche la potenza scambiata per convezione, infatti si ha:
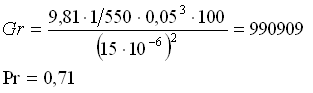
Si tratta ancora di moto laminare.

Lo scambio termico convettivo non è vero che è di assoluta proporzionalità con il salto di temperatura perché il coefficiente di convezione dipende dalla temperatura, anzi è poi una dipendenza che va a calare il coefficiente di convezione, infatti la potenza convettiva risulta:
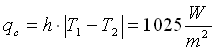
Se alziamo di altri 200 gradi le temperature, lo scambio per irraggiamento supera nettamente quello convettivo, che a queste temperature risultano ancora confrontabili tra loro.
Dentro la canna fumaria di una caldaia, dove ho la fiamma a 1500 K-1800 K, lo scambio convettivo sarà il 5-8 % dello scambio complessivo, ma il grosso dello scambio termico è legato all’irraggiamento.
Questo vuol dire che a basse temperature predominano gli effetti convettivi mentre ad alte temperature predominano gli effetti radianti.
Passiamo ora ad un analogo problema in geometria curva, in particolare andiamo a studiare il caso di un corpo che circonda completamente un secondo corpo, ovvero una cavità che chiameremo superficie ![]() , che si trova ad una temperatura
, che si trova ad una temperatura ![]() , dentro la quale è contenuta un secondo corpo con superficie
, dentro la quale è contenuta un secondo corpo con superficie ![]() che si trova a sua volta alla temperatura
che si trova a sua volta alla temperatura ![]() .
.
Prima di iniziare ci serve definire una quantità che non abbiamo ancora considerato che è il FATTORE DI FORMA o FATTORE DI VISTA (si tratta di un concetto geometrico non termico).
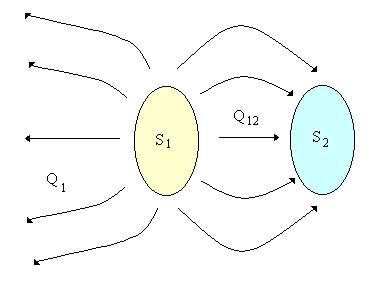
Indichiamo con:
![]() la quantità di calore che emessa dal corpo 1 va a finire sul corpo 2;
la quantità di calore che emessa dal corpo 1 va a finire sul corpo 2;
![]() la quantità di calore emessa dal corpo 1 ovunque essa vada a finire.
la quantità di calore emessa dal corpo 1 ovunque essa vada a finire.
Il fattore di vista![]() è definito come rapporto tra
è definito come rapporto tra ![]() e
e ![]() ovvero è la frazione dell’energia che un corpo emette e che va a finire su un particolare corpo.
ovvero è la frazione dell’energia che un corpo emette e che va a finire su un particolare corpo.
Se abbiamo ho un corpo che ne vede tanti e complessivamente tutti questi corpi rappresentano il suo orizzonte perché è completamente circondato da essi
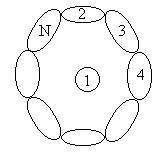
abbiamo diversi fattori di vista, cioè avrò ![]() ,
,![]() …
… ![]() .
.

La somma di tutti i fattori di vista da un corpo verso tutti gli altri che lo circondano è sempre uno.
Se i corpi sono solamente due è chiaro che quello che un corpo non dà all’altro lo dà a se stesso; è il caso di quello che accade in questo caso:
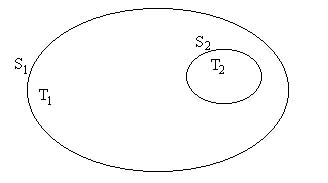
Il fattore di vista ![]() rappresenta la quantità di calore che messa dalla superficie 1 piove addosso alla superficie 2 e avrà un valore minore di uno, perché la superficie 2 è più piccola della superficie 1: esistono quantità di energia che vengono emesse e ripiovono sulla superficie1.
rappresenta la quantità di calore che messa dalla superficie 1 piove addosso alla superficie 2 e avrà un valore minore di uno, perché la superficie 2 è più piccola della superficie 1: esistono quantità di energia che vengono emesse e ripiovono sulla superficie1.
![]()
dove ![]() è la porzione di energia che dal corpo 1 torna su se stesso.
è la porzione di energia che dal corpo 1 torna su se stesso.
Quanto vale il fattore di vista ![]() ? In questo caso specifico il calcolo è particolarmente semplice perché quando andiamo a valutare le cose dal punto di vista del corpo 2 verso il corpo 1 ho che tutta l’energia emessa da 2 va a finire su 1, cioè
? In questo caso specifico il calcolo è particolarmente semplice perché quando andiamo a valutare le cose dal punto di vista del corpo 2 verso il corpo 1 ho che tutta l’energia emessa da 2 va a finire su 1, cioè
![]()
Se andiamo a fare un bilancio dell’energia posso dire, mettiamoci in condizioni isoterme, cioè ![]() e che il corpo 2 deve essere in equilibrio, cioè riceve tanto quanto emette.
e che il corpo 2 deve essere in equilibrio, cioè riceve tanto quanto emette.
La quantità di energia che emette sarà:
![]()
la quantità che riceve è la frazione ![]() dell’energia
dell’energia ![]() emessa dal corpo 1, che supponiamo nero, quindi:
emessa dal corpo 1, che supponiamo nero, quindi:
![]()
![]()
Ricaviamo così la quantità scambiata dal corpo 2 :
![]() (1.3)
(1.3)
Ricordando le ipotesi fatte, cioè condizione isoterme e di equilibrio del corpo 2, ricaviamo semplicemente:
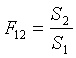
cioè il fattore di vista è pari al rapporto delle due superfici.
Questo è un caso particolarmente semplice, per casi geometricamente più complessi occorre calcolare degli integrali di superficie per calcolare il fattore di vista. Devo prendere, nel caso generico, un elemento di superficie ![]() e un altro elemento di superficie
e un altro elemento di superficie ![]() .
.
I due elementi di superficie distano una distanza r. dovremmo andare a calcolare la quantità infinitesima di calore![]() che si scambiano.
che si scambiano.
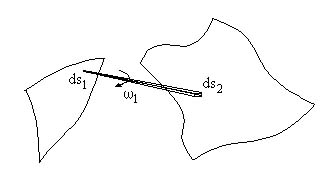
In generale la normale ![]() forma un angolo
forma un angolo ![]() con la superficie
con la superficie ![]() .
.
Occorre anche fare attenzione perché ![]() non è detto che sia normale rispetto al raggio che la congiunge con la
non è detto che sia normale rispetto al raggio che la congiunge con la ![]() , in generale il raggio r forma con
, in generale il raggio r forma con ![]() un angolo
un angolo ![]() .
.
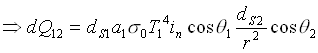
e questo è l’elemento infinitesimo del secondo ordine di cui bisogna fare un integrale doppio per ricavare ![]() , integrando sulla superficie
, integrando sulla superficie ![]() e sulla superficie
e sulla superficie ![]() , tenendo presente che i termini
, tenendo presente che i termini ![]() cambiano a seconda degli elementi di superficie che si stanno considerando.
cambiano a seconda degli elementi di superficie che si stanno considerando.
Nel caso che stavamo considerando era molto semplice il calcolo del fattore di vista che risulta semplicemente uguale al rapporto tra le superfici.
Ora si tratta di ripetere il ragionamento che abbiamo fatto prima per le superfici piane e parallele per trovare la potenza scambiata sulla superficie del corpo 2.
In realtà il calcolo è già stato impostato perché l’espressione (1.3) che abbiamo scritto sopra è corretta nel caso in cui abbiamo un corpo 1 nero.
Se la superficie esterna è nera, cosa che si verifica tutte le volte che essa è grande, poiché ![]() possiamo riscrivere in questo modo l’espressione della potenza scambiata:
possiamo riscrivere in questo modo l’espressione della potenza scambiata:
![]() (1.4)
(1.4)
Questa espressione è valida tutte le volte che abbiamo un corpo piccolo dentro a una grossa cavità che può essere trattata come un corpo nero.
Esiste poi il caso generico in cui di effettua un calcolo simile a quello che fatto tra superfici piane e grigie.
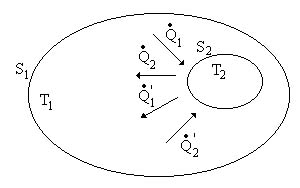
Il corpo 1 emette una quantità di calore ![]() e ne riceve una quantità
e ne riceve una quantità![]() .
.
Il corpo 2 emette una quantità di calore ![]() e ne riceve una quantità
e ne riceve una quantità ![]() .
.
Si può ora impostare un sistema di due equazioni in due incognite lineare da cui si ricava ![]() e
e ![]() .
.
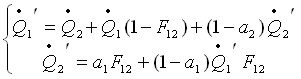
La potenza scambiata può essere espressa in questo caso come:
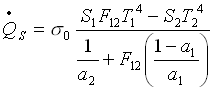
oppure andando a sostituire ![]() con la sua espressione
con la sua espressione

Si possono notare due cose:
torniamo al caso del corpo nero e ritroviamo l’espressione (1.4) trovata prima.
Allo stesso risultato si arriva per 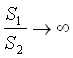 , cioè
, cioè ![]() , cioè quando il corpo interno è molto piccolo rispetto alla cavità, cioè quando un corpo è molto piccolo rispetto alla cavità è come se la cavità fosse nera.
, cioè quando il corpo interno è molto piccolo rispetto alla cavità, cioè quando un corpo è molto piccolo rispetto alla cavità è come se la cavità fosse nera.
Se il buco è piccolo qualunque sia il materiale di cui è fatta la cavità è sempre un corpo nero perché il suo assorbimento diventa totale.
L’ultima espressione che abbiamo trovato è quindi la più generica di tutte che comprende in sé, sia il caso di superfici piane affacciate entrambe grigie, sia il caso delle superfici concentriche qualunque sia il rapporto tra le superfici.
Esercizio1
Consideriamo il caso di un forno industriale di queste dimensioni:
![]() - diametro del forno
- diametro del forno
![]()
![]() - lunghezza.
- lunghezza.
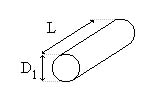
Si chiede di determinare la potenza scambiata per irraggiamento.
Siamo nel caso di un corpo piccolo dentro ad un ambiente molto più grande, che è il capannone industriale dentro cui questo forno è stato montato, quindi per calcolare la potenza complessiva possiamo utilizzare l’espressione semplificata:
![]()
Troviamo un valore effettivamente un po’ dispendioso, perché questa è la potenza che devo spendere in riscaldamento per mantenere caldo il forno affinché al suo interno avvenga la reazione chimica che desideriamo.
Dovremmo quindi utilizzare un bruciatore che soffi dentro a questo forno i prodotti della combustione che compensino questa forte dispersione verso l’esterno.
L’unica schermatura che si pensa di fare è attorno al camino principale installando un secondo foglio di lamiera ad una certa distanza che abbia queste caratteristiche:
.
L’altro grosso vantaggio è che questo schermo fa anche da schermo di sicurezza meccanica perché ho un corpo rotante che non è bene lasciare in vista, infatti avere un rivestimento che non ruota è un fattore di sicurezza dal punto di vista degli incidenti sul lavoro.

Ora la potenza scambiata tra la superficie 1 del forno e la superficie 2 dello schermo non è più calcolabile con l’espressione semplificata perché non è più vero che il corpo 1 è piccolo rispetto al corpo 2.
Inoltre non conosco la temperatura ![]() dello schermo.
dello schermo.
Ora abbiamo due corpi e quindi abbiamo anche due equazioni. Posso scrivere lo scambio termico tra il forno e lo schermo e tra lo schermo e l’esterno.
Allora andiamo a scrivere la potenza scambiata in entrambi i casi.
Si tratta di due resistenze termiche in serie:
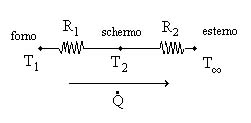
Posso scrivere la potenza termica scambiata sulla prima resistenza che va dal forno allo schermo e sulla seconda resistenza che va dallo schermo all’esterno e lo stesso flusso le percorre entrambe. Nel primo caso utilizziamo l’espressione completa, nel secondo caso possiamo utilizzare invece l’espressione semplificata:
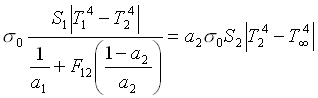
da questa espressione posso ricavare ![]() o risolvendola analiticamente, che può risultare piuttosto complesso oppure risolverla per tentativi. Comunque operando in un modo o in un altro si giunge ad un valore di
o risolvendola analiticamente, che può risultare piuttosto complesso oppure risolverla per tentativi. Comunque operando in un modo o in un altro si giunge ad un valore di ![]() pari a:
pari a:
![]()
chiaramente un valore intermedio tra la temperatura del forno e la temperatura esterna.
Ora che conosciamo la temperatura dello schermo possiamo calcolare il flusso che risulta:
![]()
Il risultato che abbiamo ottenuto è soddisfacente perché con un intervento di protezione molto limitato come costo e impegno abbiamo ridotto ad un terzo la dissipazione di energia del forno.
Il trucco non è tanto che abbiamo messo un materiale isolante, infatti abbiamo utilizzato un foglio di lamiera la cui resistenza termica è stata assolutamente trascurata, abbiamo invece interrotto la dipendenza fra la differenza della quarta potenza delle temperature, il solo fatto di introdurre uno schermo intermedio ha diminuito la temperatura e di conseguenza anche la potenza.
Anche se il fenomeno va con la quarta potenza della temperatura si calcola ugualmente una pseudo resistenza termica di irraggiamento. Questo lo si fa quando si deve combinare la resistenza termica di irraggiamento con le altre resistenze termiche (convezione, conduzione).
Si imposta quindi un legame lineare tra potenza e temperatura quando lineare non è, cioè si scrive:
![]()
dove ![]() è il coefficiente di irraggiamento e non è affatto costante, ma dipende fortemente dalla temperatura, infatti si ricava facilmente che
è il coefficiente di irraggiamento e non è affatto costante, ma dipende fortemente dalla temperatura, infatti si ricava facilmente che

possiamo sommare il coefficiente di irraggiamento al coefficiente di conduzione ![]() e trovare il coefficiente di adduzione complessivo come somma dei due e risolvere problemi più complessi.
e trovare il coefficiente di adduzione complessivo come somma dei due e risolvere problemi più complessi.
Esercizio 2
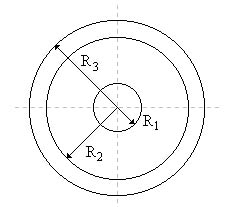
Prendiamo ora il caso di un tubo con una guaina isolante attorno e supponiamo che nel tubo scorra acqua fredda.
I dati del problema sono i seguenti:
![]() - raggio interno del tubo
- raggio interno del tubo
![]() - raggio esterno
- raggio esterno
![]() - raggio dell’isolante
- raggio dell’isolante
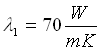 - conducibilità del tubo
- conducibilità del tubo
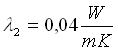 - conducibilità dell’isolante
- conducibilità dell’isolante
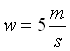 - velocità dell’acqua nel tubo
- velocità dell’acqua nel tubo
La temperatura dell’aria esterna è ![]() , la temperatura dell’acqua all’interno del tubo è
, la temperatura dell’acqua all’interno del tubo è ![]() il tubo porta acqua fredda quindi ci mettiamo l’isolante per evitare che si formi la condensa sulla superficie esterna del tubo per il fenomeno della rugiada nella miscela di aria vapore che c’è nell’aria esterna.
il tubo porta acqua fredda quindi ci mettiamo l’isolante per evitare che si formi la condensa sulla superficie esterna del tubo per il fenomeno della rugiada nella miscela di aria vapore che c’è nell’aria esterna.
Facendo riferimento al diagramma psicometrico si determina la temperatura di rugiada ![]() quindi se garantiamo una temperatura di parete esterna di 10°C evitiamo il fenomeno della rugiada.
quindi se garantiamo una temperatura di parete esterna di 10°C evitiamo il fenomeno della rugiada.
È un problema di verifica non di progetto infatti si tratta di verificare se lo spessore dell’isolante è sufficiente o meno.
Per un tubo da 17mm l’isolante da 20mm è il più piccolo che possiamo prendere in considerazione.
Dal punto di vista delle resistenze termiche questo problema può essere così schematizzato:
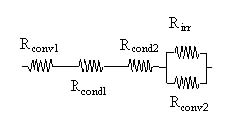 Dobbiamo trovare le resistenze termiche di ciascuno di questi blocchi.
Dobbiamo trovare le resistenze termiche di ciascuno di questi blocchi.
Cominciamo a trovare il valore della resistenza termica di convezione interna.
Si calcola subito Re utilizzando il valore della velocità e della viscosità dell’acqua a 5°C:
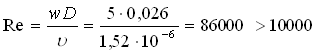 quindi il moto è turbolento.
quindi il moto è turbolento.
Dalle tabelle si ricava Pr per l’acqua a 5°C: ![]() .
.
Si ricava dalla formula di Dittus-Boelter il numero di Nusselt:
![]()
Ricordando che  si ricava il coefficiente di convezione interna:
si ricava il coefficiente di convezione interna:
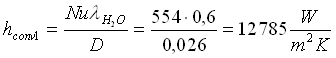
La resistenza termica di convezione interna risulta:
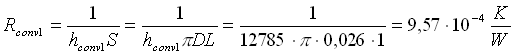 .
.
Calcoliamo ora la resistenza termica di conduzione del tubo d’acciaio.

notiamo immediatamente che è dello stesso ordine di grandezza della prima resistenza.
Troviamo nello stesso modo la resistenza termica di conduzione dell’isolante:

Queste resistenza predomina nettamente sulle prime due, che quindi si possono trascurare. Il nostro schema si può così semplificare:
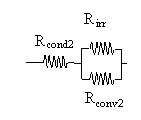
Ci rimane da calcolare il parallelo tra la resistenza di irraggiamento e la resistenza convettiva esterna.
Cominciamo a calcolarci il coefficiente convettivo esterno.
Troviamo subito Gr:

Si tratta quindi di convezione naturale e moto laminare.
Ricaviamo il numero di Nusselt:
![]()
e troviamo il coefficiente di convezione esterna:
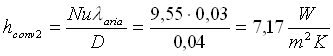 .
.
Infine calcoliamo il coefficiente di irraggiamento ![]() .
.
Dobbiamo assegnare, per il calcolo, al materiale isolante un coefficiente di assorbimento, ad esempio:
![]()
Sicuramente il tubo è piccolo rispetto all’ambiente quindi utilizziamo la formula semplificata:
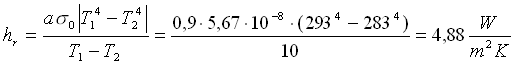 .
.
Il coefficiente di adduzione totale risulta:

da cui si ricava la resistenza totale, pari al parallelo delle due resistenze ![]() e
e ![]() :
:
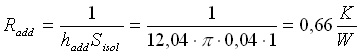
Abbiamo due resistenze quasi uguali:
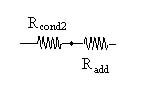
Al nodo intermedio ho una temperatura pari a 12,5°C, che è maggiore di 10°C, quindi il fenomeno della condensa sulla superficie del tubo non si verifica.