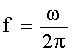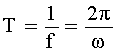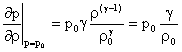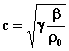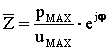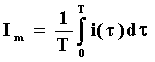che rappresentano, per ciascun
punto dello spazio dove sta andando il fluido di cui ne vogliamo studiare il
moto, la sua accelerazione e la sua velocità.
Nel caso che stiamo considerando lo spostamento avviene
lungo l’asse x (per tale motivo i
vettori che si utilizzeranno sono 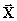 ,
,  ,
, 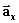 ) e le particelle di fluido si muovono di un moto di tipo
oscillatorio attorno alla posizione di equilibrio che ha spiccate analogie con
quello che in meccanica si studia come il moto di un pendolo: le oscillazioni
semplici di un pendolo che va avanti e indietro attorno alla sua posizione di
equilibrio coincidono con le oscillazioni delle particelle d’aria.
) e le particelle di fluido si muovono di un moto di tipo
oscillatorio attorno alla posizione di equilibrio che ha spiccate analogie con
quello che in meccanica si studia come il moto di un pendolo: le oscillazioni
semplici di un pendolo che va avanti e indietro attorno alla sua posizione di
equilibrio coincidono con le oscillazioni delle particelle d’aria.
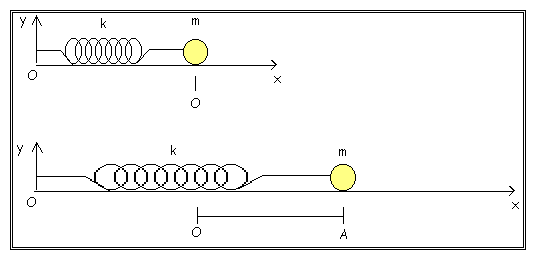
Figura 2 – Oscillazione di una particella d’aria
attorno alla sua posizione di equilibrio
Nota preliminare:
teoria del moto armonico
Il moto armonico si ha ogni qualvolta la forza di
richiamo su una particella spostata dalla posizione d'equilibrio è
proporzionale allo spostamento. Esempi comuni di un tale moto sono un corpo
attaccato
una
molla e un pendolo semplice (per piccoli spostamenti dall'equilibrio).
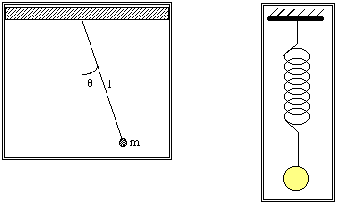
Figura 3
Il moto armonico trova inoltre applicazioni nello
studio delle onde sia sonore, sia elettromagnetiche e, in generale, di tutti i
fenomeni di tipo periodico.
Più in generale diremo moto armonico il moto
individuato su un diametro della circonferenza (o su una retta qualsiasi
parallela al diametro medesimo) da un punto che si muove di moto circolare
uniforme sulla circonferenza medesima.
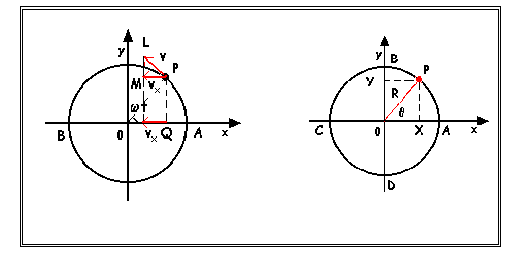
Figura 4
Detto P il punto che si muove di
moto circolare uniforme con velocità angolare 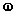 sulla circonferenza di raggio R e sia
sulla circonferenza di raggio R e sia 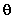 la sua posizione angolare in un generico
istante t.
la sua posizione angolare in un generico
istante t.
Quando P percorre la
circonferenza, le sue proiezioni sui due assi, rappresentate dai punti X e Y, si muovono avanti e indietro sugli assi, oscillando attorno al
centro O della circonferenza. In
particolare quando P si muove da A verso B, la proiezione X si
muove da A verso O; quando P va da B a C, X
va da O verso C; quando P va da C a D, X ritorna da C verso O e quando P conclude il
giro da D ad A, X ritorna da O verso A.
Il tempo impiegato dal
punto che si muove di moto armonico a percorrere l'intero diametro e ritornare alla
posizione di partenza (oscillazione completa) coincide con il tempo impiegato
dal punto per percorrere l'intera circonferenza. Il periodo di un'oscillazione
completa del moto armonico coincide
con il periodo del moto circolare.
Quindi il moto armonico avrà anche la stessa frequenza e la stessa velocità
angolare del moto circolare uniforme.
Inoltre dalla figura si ricava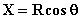 , ma trattandosi di moto circolare uniforme, vale la
relazione
, ma trattandosi di moto circolare uniforme, vale la
relazione  dove
dove 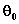 è la posizione
angolare iniziale
è la posizione
angolare iniziale
Quindi la legge oraria del moto
armonico semplice è:
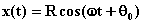 . (1)
. (1)
Tale formula giustifica il nome ampiezza assegnato a R, che costituisce il massimo valore assoluto di x; la quantità 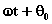 si chiama fase, la quantità
si chiama fase, la quantità 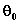 si chiama costante di
fase. D'ora in poi supponiamo che la costante di fase sia zero.
si chiama costante di
fase. D'ora in poi supponiamo che la costante di fase sia zero.
La velocità 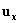 del moto armonico è la proiezione sull'asse x della velocità u del moto circolare di P.
del moto armonico è la proiezione sull'asse x della velocità u del moto circolare di P.
Si può dedurre che la velocità è:
·
nulla agli estremi A e C di oscillazione;
·
massima al centro O di oscillazione;
·
negativa da A a C;
·
positiva da C ad A.
La sorgente sonora è
normalmente una superficie mobile; dunque per studiare l’origine fisica del suono
e meglio comprendere il meccanismo della propagazione nel mezzo si può fare
riferimento alla classica esperienza del cilindro
con un pistone in grado di muoversi di moto alternato lungo l’asse
longitudinale; potrebbe essere, per esempio, il cono mobile di un altoparlante.
Si supponga che il tubo sia riempito con un mezzo comprimibile (per esempio
l’aria) e che sia tanto lungo da potere trascurare le riflessioni all’altro
estremo. Se il pistone si muove alternativamente avanti e indietro, produce nel
mezzo compressioni alternate a rarefazioni. A causa delle forze di tipo
meccanico interne al mezzo, le compressioni e le rarefazioni si propagano lungo
il tubo.

Figura 5 – Onda
longitudinale
Tale velocità viene a sua volta imposta alle particelle a
contatto con il pistone, le quali, per l’ipotesi dell’aderenza, seguono la
parete solida e vengono trascinate con sé; queste a loro volta muovono le
particelle successive e così via.
Dunque il moto è originato dall’imposizione di una
velocità al contorno ovvero si può dire che la condizione al contorno del campo
fisico è una velocità. Il modo più semplice per imporre questa velocità è
attraverso un albero rotante con una
biella; L’albero ruota attorno al suo centro con una velocità angolare 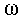 [
[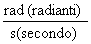 ] e ha un certo disassamento
della biella di R; quindi la
legge del moto che il pistone segue è di tipo armonico:
] e ha un certo disassamento
della biella di R; quindi la
legge del moto che il pistone segue è di tipo armonico:
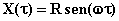 (2)
(2)
per cui la velocità
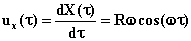 (3)
(3)
per cui l’accelerazione
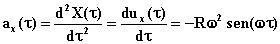 (4)
(4)
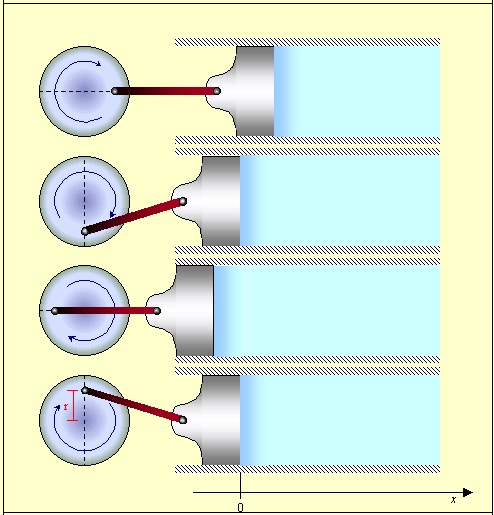
Figura 6 – Pistone generatore di onde acustiche
L’aria è un mezzo elastico cosicché, muovendo in avanti il
pistone per un piccolo tratto, se ne comprime l’elemento diretto a contatto con
la superficie del pistone e quindi si provoca un aumento locale di pressione.
Aumentando il movimento del pistone, l’elasticità dell’aria provoca allora
un’espansione nella direzione di allontanamento del pistone (in quanto questo è
un corpo rigido).
Le molecole che costituiscono l’elemento d’aria in
pressione spingono allora quelle costituenti l’elemento adiacente
comprimendolo; in questo modo, per spinte successive, ha luogo la propagazione,
lungo il condotto, della perturbazione causata dal movimento del pistone.
Muovendo il pistone in senso opposto ha luogo esattamente lo stesso fenomeno:
una momentanea depressione dell’elemento d’aria richiama altro gas dal volume
adiacente che a sua volta lo richiama da quello precedente e così via; in
questo caso si ha però un valore negativo della pressione. Pressioni positive e
negative sono intese come valori superiori o inferiori a quello della pressione
atmosferica del gas (aria) posto nel tubo in condizioni di riposo.
L’orecchio umano è lo strumento in grado di farci
percepire le variazioni di pressione come fenomeni acustici; queste
perturbazioni generate dal movimento del pistone non sono però percepibili come
suono dall’orecchio: se un singolo fronte d’onda raggiunge il nostro orecchio
noi possiamo percepire un “colpo” con un tono secco o sordo che dipende dalla
velocità con cui è stato mosso il pistone.
Per avere una vera e propria generazione di suono è
necessario di una serie continua di onde di pressione che equivale a muovere
continuamente avanti e indietro il pistone con una certa velocità.

Figura 7 – Diagramma orario di un moto armonico
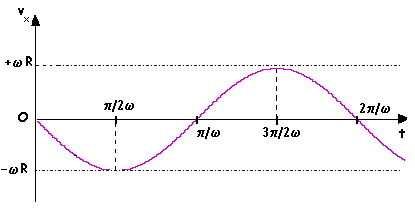
Figura 8 – Diagramma velocità – tempo di un moto
armonico

Figura 9 – Diagramma accelerazione – tempo di un
moto armonico
I
grafici delle equazioni del moto armonico sono rappresentati nelle figure
limitatamente a un periodo, cioè al tempo 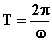
Dall'osservazione del
diagramma orario si possono dedurre le seguenti proprietà:
·
per  e per
e per 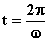 il punto Q
(proiezione del punto P sull'asse x) si trova nell'estremo A di oscillazione;
il punto Q
(proiezione del punto P sull'asse x) si trova nell'estremo A di oscillazione;
·
per 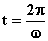 il punto Q si trova
nell'estremo B di oscillazione;
il punto Q si trova
nell'estremo B di oscillazione;
·
per 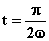 e per
e per 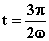 il punto Q passa
attraverso il centro O di oscillazione.
il punto Q passa
attraverso il centro O di oscillazione.
Dall'osservazione del
diagramma orario si può dedurre il diagramma velocità – tempo. Tenendo conto che la velocità è la
pendenza della retta tangente al diagramma orario, si ha che la velocità è:
·
nulla agli estremi A
e C di oscillazione dove la pendenza della tangente è zero;
·
massima al centro O
di oscillazione dove la pendenza della tangente è massima;
·
negativa da A a C;
·
positiva da C ad A.
Analogamente, essendo
l'accelerazione la pendenza al grafico velocità – tempo, si ha che l'accelerazione è:
·
nulla nel centro O
di oscillazione dove la pendenza della tangente è zero (per  e per
e per 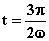 );
);
·
massima in valore
assoluto agli estremi A e C di oscillazione dove è massima la pendenza della
tangente (per 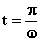 e per
e per 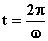 );
);
·
negativa da A a O e
da O ad A;
·
positiva da O a C e
da C a O.
La particella d’aria immediatamente a contatto con il
pistone segue questa legge di tipo armonico, ma cosa succede alle particelle
d’aria che stanno più in là non è così scontato, ovvero potrebbe variare la
legge del moto (non è detto che questa legge si trasmette tale e quale a
qualunque distanza dalla superficie a contatto col pistone). In generale si ha
una variazione di ampiezza: normalmente allontanandosi dalla sorgente il campo
si estingue; l’ampiezza dell’oscillazione si riduce e contemporaneamente si
hanno degli sfasamenti poiché la propagazione non avviene in un tempo nullo (il
suono impiega del tempo a spostarsi nell’aria dato che ha una velocità di
propagazione finita). Quella che non varia è la frequenza, infatti si ipotizza
che tutti i fenomeni che riguardano il campo acustico siano lineari.
Un sistema (che può
comprendere non solo il campo acustico) si dice lineare se:

applichiamo in ingresso al sistema un segnale d’ingresso A e il sistema risponde
con un segnale  ; analogamente per un segnale d’ingresso B. Allora:
; analogamente per un segnale d’ingresso B. Allora:

 (5)
(5)
Dunque
un sistema è lineare si gode della proprietà additiva sia all’ingresso che
all’uscita: se sommo due segnali in ingresso,
all’uscita trovo la somma delle risposte che ciascun segnale da solo mi dava
(il nostro è il caso particolare in cui A e B sono uguali).
Il campo acustico è un sistema lineare fino a livelli
sonori altissimi: il problema di avere fenomeni non lineari nell’aria in cui
devono vivere degli esseri viventi non si pone; esistono nella tecnologia
moderna eventi in cui si ha a che fare con fenomeni di propagazione acustica
fortemente non lineari (per esempio: scarico di un reattore, esplosione di una bomba
atomica). Le onde che si propagano non si chiamano più onde acustiche ma onde
d’urto, che non vengono studiate dall’acustica. La non linearità può
presentarsi nei trasduttori, in particolare negli altoparlanti; essi sono
dispositivi altamente non lineari: il segnale che esce dall’altoparlante è
composto anche da distorsioni che non fanno parte del fenomeno della
propagazione acustica, ma di fenomeni elettromagnetici: una volta che una certa
legge del moto è stata prescritta all’aria dal cono che si muove
dell’altoparlante, l’aria propaga questa legge del moto in maniera
perfettamente lineare.
Il concetto importante è comunque che se ad un sistema
lineare applico in ingresso un’eccitazione che è un segnale armonico semplice,
in uscita si può avere una variazione di ampiezza e velocità del segnale, ma
non di frequenza. Mentre, se il sistema genera una risposta a frequenza diversa
da quella dell’eccitazione, allora questo è sintomo di non linearità.
Definiamo le principali grandezze utilizzando le leggi del
moto armonico:
SUONO PURO (detto anche tono
puro) è una legge del moto rappresentata graficamente da un’unica
sinusoide; per un suono puro le grandezze fondamentali che si definiscono sono
·
la frequenza f (numero
di giri che fa il motore di quell’albero nell’unità di tempo):
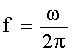 [
[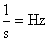 (Hertz)] (6)
(Hertz)] (6)
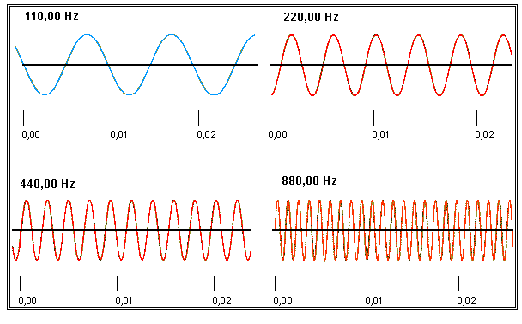
Figura 10 - Differenza tra i suoni
generati da onde di uguale ampiezza,
ossia con la medesima intensità, e
con frequenze
che siano in rapporto di 2 a 1
·
il periodo T
(inverso della frequenza, è un’oscillazione completa che mi riporta al punto di
partenza ovvero il tempo necessario affinché il sistema completi
un’oscillazione e si rimetti nella condizione da cui è partito):
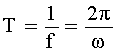 [s (secondo)] (5)
[s (secondo)] (5)
Quando un suono ha una forma d’onda caratterizzata da una
legge che si ripete sempre uguale a se stessa dopo un certo intervallo, si
chiama un suono periodico. Dunque il
suono puro è un suono periodico; eppure esistono suoni non puri che sono
periodici (forma d’onda complicata come il dente di sega che viene ripetuta
sempre uguale e dunque esiste un periodo di ripetizione). La periodicità non è
garanzia di purezza:

·
l’ampiezza A (parlando di velocità, valore massimo
che la forma d’onda assume).
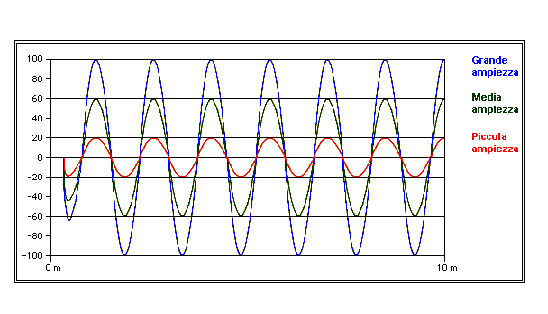
Figura 11 – Ampiezza e volume:
L'ampiezza dell'onda è la proprietà fisica che determina
il volume dei suoni. Essa rappresenta lo spostamento massimo delle molecole
d'aria che oscillano intorno alla posizione di equilibrio al passaggio della
perturbazione acustica. All'aumentare di questo spostamento aumenta la forza
con cui le molecole colpiscono la membrana timpanica e, quindi, l'intensità del
suono che percepiamo. Le tre onde qui rappresentate sono caratterizzate dalla
stessa frequenza: producono il suono della stessa nota, ma vengono udite a
volume diverso.
Dunque
la legge del moto delle particelle dell’aria può essere scritta come:
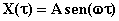 (6)
(6)
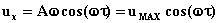 (7)
(7)
Il suono possa
diffondersi, il mezzo attraverso cui viaggiano le onde sonore deve essere elastico,
dunque ritornando al caso del pistone mobile, si può dire che la compressione
dell’aria (essendo un mezzo elastico), dovuta all'avanzata del pistone, viaggia
con velocità finita.
Quindi ad un determinato
istante di tempo e ad una opportuna distanza dal pistone, esisterà sempre uno
strato di particelle rimaste ferme che costituisce una barriera all'avanzamento
delle particelle perturbate dal moto del pistone. Si ha il cosiddetto fenomeno
di confinamento inerziale il quale
fa sì che, sebbene non vi sia una parete solida, il volume del gas diminuisca e
che, di conseguenza, aumenti la pressione. Quando il pistone torna indietro, il
volume e la pressione ritornano ai loro valori originari: anche la pressione
segue il moto del pistone fluttuando nel tempo con legge sinusoidale.
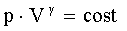 (8)
(8)
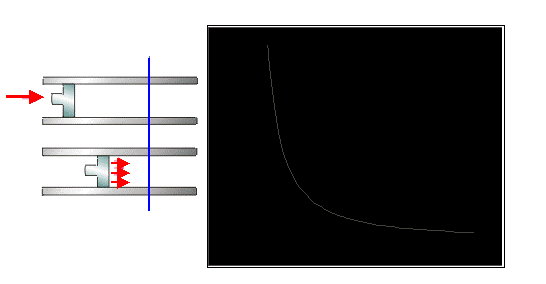
Figura 12 – Compressione del pistone e relativo
grafico di oscillazione della pressione
in funzione del volume
Il sistema , seguendo
questa legge, oscillerà intorno al punto (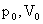 ) , cioè intorno alla pressione atmosferica. Quando il suono
si propaga, dobbiamo accettare il fatto che non c’è solo il moto della
particella, ma questo moto è anche accompagnato da fluttuazioni della pressione in un punto; questo corrisponde,
nel caso del pendolo, al fatto che l’energia si trasforma periodicamente da
potenziale a cinetica e viceversa (il pendolo è un sistema conservativo).
) , cioè intorno alla pressione atmosferica. Quando il suono
si propaga, dobbiamo accettare il fatto che non c’è solo il moto della
particella, ma questo moto è anche accompagnato da fluttuazioni della pressione in un punto; questo corrisponde,
nel caso del pendolo, al fatto che l’energia si trasforma periodicamente da
potenziale a cinetica e viceversa (il pendolo è un sistema conservativo).

Figura 13 – Pendolo semplice
Anche nel campo acustico succede
qualcosa del genere, ovvero, pur non essendo un sistema conservativo (nel campo
acustico l’energia entra da una parte ed esce dall’altra; ovvero dal punto di
vista energetico è un sistema di trasporto di energia, e dunque aperto: c’è una
fonte che produce energia e c’è un recettore che l’assorbe), nel corso della
propagazione si ha un periodico travasarsi di energia tra la sua forma cinetica
e la sua forma potenziale. Dalla legge del moto si nota che ci sono degli
istanti in cui le particelle hanno velocità nulla; quando la velocità di una
particella è nulla, è inevitabilmente nulla l’energia cinetica associata alla
particella. Però il primo principio di
conservazione dell’energia insegna che l’energia non si crea e distrugge,
ma si trasforma, dunque in questa situazione essa è immagazzinata sotto forma
di energia potenziale, ma non energia potenziale gravitazionale come nel caso
del pendolo che oscilla; in tale istante le particelle dispongono di energia
potenziale poiché si trovano momentaneamente ad una pressione diversa da quella
atmosferica. Quindi così come oscilla la particella attorno alla sua posizione
di equilibrio, così oscilla anche la pressione. Il contributo cinetico è
fruibile fino a che la particella è in movimento; quando questa si ferma per un
attimo primo di riportarsi nella posizione iniziale, l’energia immagazzinata
diventa potenziale, presente nel campo sonoro appunto sotto forma di pressione.
Se vado a diagrammare
l’andamento della pressione (pressione atmosferica in assenza della perturbazione
causata dal campo acustico) nel tempo, avendo definito con  la pressione acustica, che non è la
pressione totale nel punto, ma una pressione relativa poiché è la differenza
tra la pressione istantanea
la pressione acustica, che non è la
pressione totale nel punto, ma una pressione relativa poiché è la differenza
tra la pressione istantanea 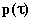 e la pressione atmosferica media
e la pressione atmosferica media 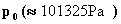 nel punto
considerato:
nel punto
considerato:
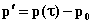 (9)
(9)
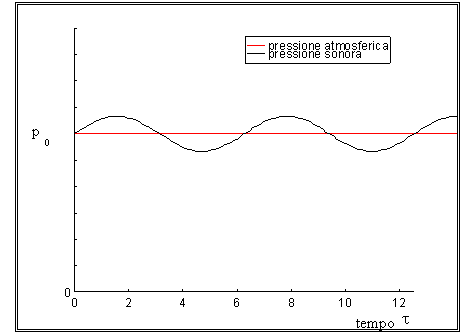
Figura 14 – Fluttuazione con legge
sinusoidale della pressione attorno alla pressione atmosferica 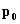
Quando due particelle si
avvicinano localmente la pressione si innalza, mentre quando due particelle
rimbalzano lontano l’una dall’altra, il gas si dirada e la pressione scende al
di sotto del valore della pressione
atmosferica. Queste fluttuazioni di pressione sono piccole, poiché la
pressione acustica è enormemente più piccola rispetto alla pressione
atmosferica: una pressione acustica di 1 Pa
( ) equivale a un livello di pressione sonora
) equivale a un livello di pressione sonora  di circa 91 dB (molto elevato e addirittura dannoso per
l’organismo umano). Dunque la fluttuazione di pressione rispetto a
di circa 91 dB (molto elevato e addirittura dannoso per
l’organismo umano). Dunque la fluttuazione di pressione rispetto a 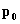 è trascurabile,
perché è un valore centomila volte più piccolo del valore medio che ha la
pressione atmosferica; stiamo quindi parlando di un fenomeno che implica un
trasporto di informazione con una minima spesa dell’energia. Una tale legge del
moto si propaga anche in istanti molto grandi con pochissima variazione: è vero
che cambierà ampiezza, che ruoterà la fase, ma la forma d’onda viene
trasportata priva di alterazioni a distanze anche notevoli e rimane
perfettamente decifrabile il significato del suono. La capacità di trasportare
informazione è grandissima in rapporto alla quantità di energia impiegata (solo
recentemente se è riusciti a trasportare lo stesso livello di informazione –
voce umana, parlando di telefonia cellulare – a distanze maggiori di quelle di
cui è in grado di fare il campo acustico impegnando potenze confrontabili con
queste). È un efficiente sistema di trasporto: con segnali dotati di pochissima
energia si è in grado di trasportare un
quantitativo di informazione notevole anche a grandi distanze.
è trascurabile,
perché è un valore centomila volte più piccolo del valore medio che ha la
pressione atmosferica; stiamo quindi parlando di un fenomeno che implica un
trasporto di informazione con una minima spesa dell’energia. Una tale legge del
moto si propaga anche in istanti molto grandi con pochissima variazione: è vero
che cambierà ampiezza, che ruoterà la fase, ma la forma d’onda viene
trasportata priva di alterazioni a distanze anche notevoli e rimane
perfettamente decifrabile il significato del suono. La capacità di trasportare
informazione è grandissima in rapporto alla quantità di energia impiegata (solo
recentemente se è riusciti a trasportare lo stesso livello di informazione –
voce umana, parlando di telefonia cellulare – a distanze maggiori di quelle di
cui è in grado di fare il campo acustico impegnando potenze confrontabili con
queste). È un efficiente sistema di trasporto: con segnali dotati di pochissima
energia si è in grado di trasportare un
quantitativo di informazione notevole anche a grandi distanze.
La propagazione dell’onda
sonora nel tubo avviene con progressivo ritardo di fase perché l’onda impiega
del tempo per propagarsi, con attenuazione pressoché nulla dell’ampiezza.
Suppongo di avere un tubo anche molto lungo (distanze chilometriche); se
introduco un segnale che dà luogo a una pressione di 1 Pa, al termine del tubo
trovo un segnale con pressione di ancora 1 Pa. Il problema che pone un tale
tipo di trasporto dell’informazione è la sua velocità, che non è né infinita né
molto grande (gli aerei supersonici volano ad una velocità superiore: il suono
che l’aereo vorrebbe buttare in avanti viaggia alla sua stessa velocità e
quindi si ammucchia tutto sul muso dell’aereo; a forza di accumularsi può
raggiungere livelli tali da diventare una vera e propria onda d’urto, spaccando in due l’aereo a causa dell’enorme
sollecitazione a cui è sottoposto l’aereo – ma in questo caso si entra a che
fare con l’acustica non lineare che è una scienza che ha più a che fare con la
gas–dinamica che con l’acustica vera e propria).
La velocità con cui l’onda sonora si propaga dentro questo
tubo si chiama 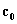 :
:
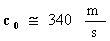 (10)
(10)
Tale velocità non dipende dalla
forma d’onda: tutti i suoni, a tutte le frequenze, ampiezze, viaggiano con la
stessa velocità. Dunque la propagazione del suono oltre ad essere un fenomeno
lineare è anche non dispersivo. Si chiamano invece dispersivi i fenomeni di
propagazione che avvengono con velocità variabile, e che tendono a distruggere
la forma d’onda del segnale tutte le volte che la stessa non è una sinusoide
perfetta: se abbiamo due sinusoidi che viaggiano con velocità differenti, si
combinano in maniera diversa rispetto a prima poiché una subisce un ritardo
maggiore dell’altra.
È bene osservare che il moto
delle particelle d’aria attorno alla
loro posizione di equilibrio non ha niente a che vedere con il moto di propagazione
dell’onda che si diffonde con un velocità c
e che è indipendente dalla legge del moto; al contrario ogni suono ha una
diversa legge del moto e dunque cambia la velocità delle particelle (u). Nel momento in cui la particella d’aria oscilla, l’energia
dell’onda è già passata, dunque si può dire che la velocità del movimento è diversa dalla velocità di movimento.
L’espressione matematica
corretta è facilmente ricavabile dalle equazioni che descrivono la pressione in
campo sonoro sono quelle dei gas perfetti, già incontrate nella termodinamica,:
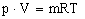
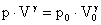 (11)
(11)
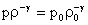
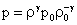
 (12)
(12)
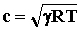 (13)
(13)
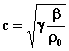 (14)
(14)
Essendo i liquidi
solitamente poco comprimibili, la velocità del suono in un mezzo di questo tipo
è spesso abbastanza elevata. Questa è anche la causa delle diffusissima
incapacità di determinare la provenienza di un suono quando siamo in
immersione; infatti la determinazione della provenienza di una suono è
principalmente basata sul tempo di ritardo che l’onda acustica accumula
nel raggiungere l’orecchio più lontano
dalla sorgente sonora. Nel corpo umano le orecchie sono distanziate circa di
170 mm; in aria la velocità del suono è di circa 340 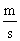 quindi un segnale
direzionato lateralmente impiega un 1 ms in più per raggiungere l’orecchio più
lontano dalla sorgente sonora rispetto a quanto impieghi a raggiungere quello
più vicino. Il tempo di ritardo aiuta quindi il cervello evolutivamente
addestrato a riconoscere la provenienza dell’onda acustica. Il nostro sistema
uditivo è infatti "calibrato" per percepire suoni provenienti
dall'aria: in base al ritardo che impiega un suono a giungere alle nostre
orecchie (IDT, interaural delay time
o ILD, interaural level difference
per le alte frequenze), capiamo da dove arriva.
quindi un segnale
direzionato lateralmente impiega un 1 ms in più per raggiungere l’orecchio più
lontano dalla sorgente sonora rispetto a quanto impieghi a raggiungere quello
più vicino. Il tempo di ritardo aiuta quindi il cervello evolutivamente
addestrato a riconoscere la provenienza dell’onda acustica. Il nostro sistema
uditivo è infatti "calibrato" per percepire suoni provenienti
dall'aria: in base al ritardo che impiega un suono a giungere alle nostre
orecchie (IDT, interaural delay time
o ILD, interaural level difference
per le alte frequenze), capiamo da dove arriva.
Osserviamo che l’azoto non
può essere considerato un gas perfetto perché la velocità del suono varia con
la pressione. E' importante osservare che, oltre all'alta velocità dell’onda
sonora, l’acqua possiede un bassissimo coefficiente
di perdita: il suono infatti può percorrere in acqua anche centinaia di
chilometri prima di perdere ampiezza.
Considerando l'esempio
del pistone e il concetto di mezzo elastico e massivo, andando a osservare
l'andamento del moto da un punto distante 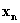 dallo stantuffo, si nota che lo strato di
particelle aderenti al pistone agisce elasticamente trasmettendo la spinta al
secondo strato dopo un certo istante di tempo; quindi l'onda sonora non si
propaga a velocità infinita, ma con la velocità c che è stata definita prima. La velocità della generica particella
( che, è importante ripeterlo, non è la velocità dell'onda ) presente nel tubo
in corrispondenza dell'ascissa
dallo stantuffo, si nota che lo strato di
particelle aderenti al pistone agisce elasticamente trasmettendo la spinta al
secondo strato dopo un certo istante di tempo; quindi l'onda sonora non si
propaga a velocità infinita, ma con la velocità c che è stata definita prima. La velocità della generica particella
( che, è importante ripeterlo, non è la velocità dell'onda ) presente nel tubo
in corrispondenza dell'ascissa 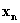 è ricavabile tramite
una traslazione nel tempo della legge vista in precedenza:
è ricavabile tramite
una traslazione nel tempo della legge vista in precedenza:
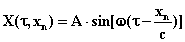 (16)
(16)
La
traslazione  non è altro che il
tempo necessario per percorrere la distanza
non è altro che il
tempo necessario per percorrere la distanza 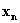 .
.
Dire che il suono viaggia con questa velocità vuol dire
che se impongo una certa legge del moto al pistone, trascorso un certo tempo,
troverò questa legge del moto identica in un punto dello spazio che sta più a
destra. Quindi conoscere la velocità del suono significa legare la legge del
moto espressa come velocità nel tempo con la legge del moto espressa come
velocità nello spazio: se ho una situazione in un certo istante 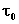 , trascorso un intervallo di tempo
, trascorso un intervallo di tempo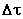 , la ritroverò invariata; Dunque il concetto di velocità del
suono non ha senso applicato al concetto di suono puro: una sinusoide è sempre
uguale a sé stessa e dunque non mi accorgo dell’importanza del concetto di
velocità del suono.
, la ritroverò invariata; Dunque il concetto di velocità del
suono non ha senso applicato al concetto di suono puro: una sinusoide è sempre
uguale a sé stessa e dunque non mi accorgo dell’importanza del concetto di
velocità del suono.
Il ritardo applicato nel
caso di un segnale acustico è un fattore spesso trascurabile, e si può
dimostrare attraverso un esempio pratico: consideriamo un’aula universitaria
lunga 13 metri ed una persona che parla dal fondo della stanza; la sua voce
giungerà all’ascoltatore con un ritardo
di:

Come si
vede benissimo, anche attraverso le normali esperienze, questo tempo non è tale
da far sembrare il suono ed il movimento delle labbra fuori sincronia, ma
ponendoci in un contesto di distanza molto più alta, e contando sul fatto che
normalmente un uomo parlando pronuncia 3 sillabe al secondo, in una distanza
dieci volte più ampia della precedente (130 m) notiamo un ritardo di :
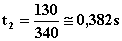
e quindi
uno sfasamento di circa una sillaba. In
realtà il valore qui sopra ricavato si
riferisce al ritardo della sola onda sonora diretta e non a quello degli
innumerevoli effetti di riflessione e riverberazione presenti negli ambienti
chiusi, che in generale possiedono un ritardo maggiore rispetto all'onda
diretta. La voce della persona arriverebbe quindi all'orecchio dell'ascoltatore
con una sorta di coda sonora derivante dalla somma di tali effetti:

Figura 15 – Coda del
tempo
Il trasporto del suono presenta
dunque questo enorme problema della lentezza: il segnale di partenza di una gara
d’atletica si traduce in una certa legge del moto e viene udito a 340 metri un
secondo dopo; il direttore di un’orchestra batte il tempo agli orchestrali
muovendo una bacchetta; essi si sentono perfettamente a tempo perché la luce ha
velocità elevata e lo strumento che percuotono è vicino a loro e non c’è
ritardo da propagazione; ma il suono prodotto dagli orchestrali impiega del
tempo a raggiungere il direttore, per cui non lo sentirà sincrono al suo
battito.
Diventa dunque complesso
riuscire a tenere assieme l’orchestra; a questo scopo si ricorre a sistemi
elettronici che captino i suoni vicino agli orchestrali e li portino tutti con
tempi molto ridotti al direttore e agli altri componenti. Il problema del
transitorio invece ha scarsissima rilevanza nella termodinamica; mentre
nell’acustica siamo sempre in regime
transitorio perché il regime stazionario non fa quasi mai in tempo a
stabilirsi: prima che il sistema raggiunga la situazione di regime, l’emissione
del suono è già terminata.
L’ultimo concetto che dobbiamo
chiarire riguardo alle leggi del moto sinusoidale è la lunghezza d’onda: se potessi fare una fotografia in un certo
istante di come varia la velocità nei vari punti all’interno del condotto,
vedrei che qui sarei nel punto di spostamento nullo (minimo) e velocità
massima; dunque se diagrammo la velocità lungo l’asse x, man mano che vado avanti trovo dei valori che stavano prima nel
tempo perché vedrò in punti dello spazio più a destra punti del tempo più a
sinistra; muovendomi verso destra vedo il passato, ossia quello che è successo
prima. A una certa distanza vedrò un valore di velocità nullo che corrisponde a
quello che era accaduto ¼ di periodo prima di tale istante. Questo diagramma mi
rappresenta dunque l’andamento della forma d’onda nello spazio, non nel tempo:
nello spazio vedo un periodo di oscillazione completa pari alla lunghezza d’onda del suono, legata alla frequenza e
alla velocità del suono dalla relazione:
Dunque dopo la distanza  vedo quello che è
accaduto T secondi prima, ovvero il
suono nel tempo T ha percorso
vedo quello che è
accaduto T secondi prima, ovvero il
suono nel tempo T ha percorso 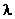 lambda metri che è c volte il tempo stesso; la lunghezza d’onda è proporzionale al periodo e inversamente proporzionale
alla frequenza:
lambda metri che è c volte il tempo stesso; la lunghezza d’onda è proporzionale al periodo e inversamente proporzionale
alla frequenza:
 (17)
(17)
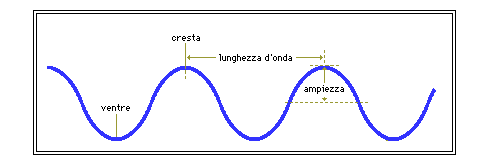
Figura 16 – Onda trasversale
La velocità del suono è praticamente una costante
(dipende dalla temperatura), quindi le lunghezze d’onda del suono variano molto
perché variano molto le frequenze che siamo in grado di udire: il nostro apparato
uditivo può percepire frequenze comprese tra 20 e 20.000 Hz (col passare degli
anni il campo delle frequenze superiori va a perdersi), ovvero c’è un fattore
1000 tra la frequenza più bassa udibile e quella più alta, e conseguentemente
c’è un’enorme differenza tra le lunghezze d’onda più basse e quelle più alte.
Un altro passaggio fondamentale
da capire è il legame tra frequenza e lunghezza d’onda, perché l’interazione
del suono con gli oggetti è diverso nel caso che l’oggetto sia molto grande o
confrontabile o molto piccolo rispetto
alla lunghezza d’onda. Nel campo della luce visibile ad esempio, le lunghezze
d’onda variano tra 0.4 e 0.7 nano metri e dunque in un intervallo strettissimo
in confronto all’intervallo acustico perché il rapporto tra la lunghezza d’onda
massima e la lunghezza d’onda minima è circa ½. Calcoliamo i corrispondenti
valori di lunghezza d’onda per avere qualche riferimento numerico:
Quindi la lunghezza d’onda è
enorme e qualunque oggetto risulta confrontabile o piccolo rispetto a 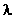 :
:
·
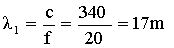 ;
;
·
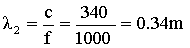 :
:
la parete del cubo è diventata
una superficie speculare per un suono con quella frequenza, perché è
enormemente più grande della lunghezza d’onda;
·
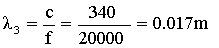 :
:
a questa frequenza, la
lunghezza d’onda comincia ad essere confrontabile con le asperità della parete,
che dunque non si comporta più come un riflettore speculare, ma diventa una
superficie scabra dove i fronti d’onda si dividono in tanti altri fronti d’onda
che si dipartono in direzioni diverse.
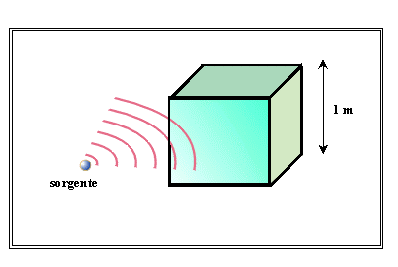
Figura 17 – Cubo investito da
un’onda sonora
Dunque una stessa superficie può essere: a bassa
frequenza inesistente perché il
suono le gira attorno rimanendo inalterato, a media frequenza speculare, ad alta frequenza diffondente.
Il suono è sempre nella stessa
natura, il fenomeno fisico non è cambiato, ma cambia la lunghezza d’onda;
dunque è difficile realizzare un trasduttore che funzioni ugualmente bene a
bassa e ad alta frequenza: a bassa frequenza, in un altoparlante ho bisogno di
coni grandi perché devono essere proporzionati alla lunghezza d’onda che devono
produrre, ma aumentando la frequenza, non ho più bisogno di superficie enormi
per produrre il suono, anzi è un male perché non riesco più a controllare le
emissioni; ecco l’impossibilità di utilizzare un unico altoparlante e l’utilità
di avere due altoparlanti, uno per le alte e uno per le basse, o addirittura
anche tre (uno per i medi), per potere far fronte a questo enorme span di
lunghezze d’onda.
Andiamo avanti con le definizioni: abbiamo visto che nel campo
acustico le grandezze fisiche che intervengono sono due: una di tipo
cinematico, ovvero la velocità delle
particelle e la fluttuazione di pressione; vediamo come
queste due grandezze interagiscono fra di loro. Ci sono due modi primari in cui
fare interagire pressione e velocità delle particelle:
·
Rapporto
fra pressione e velocità:
Mi posiziono in un punto del
tubo monodimensionale e misuro una certa p
e u; mi porto in un altro punto
muovendomi verso l’asse x e avrò un
diverso valore di p e v (dunque 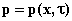 e
e  sono funzioni sia
dello spazio che del tempo).
sono funzioni sia
dello spazio che del tempo).
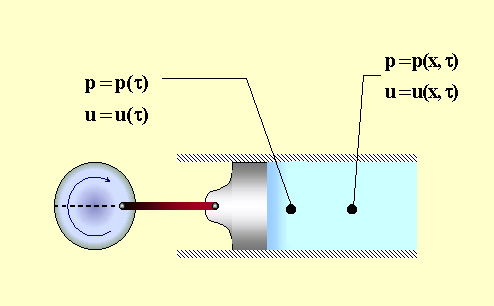
Figura 18
Il legame tra la funzione di x e
la funzione del tempo è dato dalla velocità, ma questo è vero sono nel caso di
propagazione intubata, perché sappiamo che qui il segnale rimane uguale a se
stesso e che mi basta muovermi di uno spazio pari alla lunghezza d’onda per
ritrovare lo stesso segnale (è un caso particolare di propagazione). Questo
porta a rendere la funzione non più funzione di due variabili indipendenti x e
t, ma di una variabile unica:
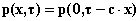 . (18)
. (18)
Negli altri casi di propagazione non è più vero: in qualunque
punto di questa stanza si stabilisce una pressione e una velocità che sono
funzione del tempo (perché non sto emettendo sempre gli stessi suoni e quindi
in ogni istante il segnale è diverso) e dello spazio (perché dipende dalla
distanza dalla sorgente e dunque dall’ampiezza del segnale che raggiunge il
ricevitore).
In generale in ogni punto le
due grandezze pressione e velocità subiscono fenomeni simili: se cala
l’ampiezza in termini di velocità, cala normalmente anche l’ampiezza in termini
di pressione, quindi le grandezze sono strettamente correlate. Questo può
essere visto facendo il rapporto tra le due: se in qualunque punto e in
qualunque istante vado a fare:
 , (19)
, (19)
definisco
la grandezza impedenza acustica che
è il rapporto tra la pressione e la velocità delle particelle.
·
1°
Problema: la velocità è un vettore, la pressione è uno scalare,
dunque prendo il modulo del vettore, senza preoccuparci di come è orientato
nello spazio perché l’impedenza è uno scalare.
·
2°
Problema: pur restando nel campo dei segnali sinusoidali, non è
detto che pressione e velocità siano in fase; in generale vedo su un
oscilloscopio a due canali logici uno
con u e l’altro con p, trovo due sinusoidi che non hanno lo
stesso punto d’origine, ma sono sfasate (parallelismo tra corrente e tensione in un circuito elettrico
alimentato con un generatore di tensione alternata). I casi in cui p e v sono in fase rappresentano un’eccezione rarissima: questo vuol
dire che normalmente l’impedenza acustica è una grandezza complessa perché è il
rapporto di due grandezze sfasate.

Figura 19 –
Oscilloscopio: è uno strumento capace di analizzare qualunque tipo di segnale
elettrico visualizzandolo sullo schermo fluorescente di un tubo a raggi
catodici. Si possono determinare così la forma, la dipendenza dal tempo e
l'ampiezza di un segnale, come pure confrontare più segnali contemporaneamente.
È un concetto delicato:
lo si fa per analogia molto stretta con lo studio delle correnti elettriche nei
conduttori, ma diventa invece ora molto difficile da vedere a livello di
comprensione fisica. Infatti l’impedenza acustica è una grandezza complessa
sebbene sia il rapporto di due grandezze che non sono affatto complesse (p e v sono grandezze assolutamente reali): è un fatto abbastanza
asimmetrico; tutto discende da una convenzione di coerenza della scelta
dell’asse dei tempi tra grandezze di tipo pressione, velocità, poiché il fatto
di avere un’origine dei tempi comune porta a definire una fase  che governa questo
fenomeno. Se prendo la pressione come riferimento, ho la seguente legge
sinusoidale:
che governa questo
fenomeno. Se prendo la pressione come riferimento, ho la seguente legge
sinusoidale:
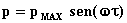 ; (20)
; (20)
se voglio ora esprimere la
velocità anch’essa con una legge sinusoidale, avrò che:
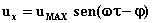 , (21)
, (21)
ovvero deve trascorrere un tempo di ritardo positivo 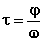 dato che l’asse delle
ascisse è un tempo; ovvero ho dovuto aspettare un certo tempo per trovare un
segnale di velocità identico al segnale di pressione (naturalmente i valori di
ampiezza saranno diversi); in una situazione di questo tipo l’impedenza vale:
dato che l’asse delle
ascisse è un tempo; ovvero ho dovuto aspettare un certo tempo per trovare un
segnale di velocità identico al segnale di pressione (naturalmente i valori di
ampiezza saranno diversi); in una situazione di questo tipo l’impedenza vale:
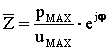 ; (22)
; (22)
il modulo è il rapporto fra i moduli e la fase è  (usando la notazione di Eulero, che sta alla base
del calcolo con grandezze complesse che si usa sia in elettrotecnica che in
acustica:
(usando la notazione di Eulero, che sta alla base
del calcolo con grandezze complesse che si usa sia in elettrotecnica che in
acustica: 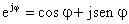 ).
).

Figura 20
Dunque, in generale l’impedenza
intesa come grandezza complessa è costituita da un’impedenza reale  e da una impedenza immaginaria
e da una impedenza immaginaria 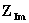 :
:
 , (23)
, (23)
dove 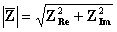
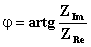
Ricapitolando: abbiamo due
grandezze fisiche (pressione e velocità), in generale anche nel caso più
semplice di moto armonico (quindi di tono puro), troveremo in ciascun punto
dello spazio e in ciascun istante che due segnali pur essendo due sinusoidi,
non sono in fase fra loro, ma c’è un certo sfasamento; quando faccio il
rapporto di queste due grandezze, trovo una grandezza con modulo pari al
rapporto dei moduli e una fase pari alla differenza tra le fasi della velocità
e della pressione.
Nota:

La
funzione arctg è definita per valori
di 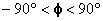 , mentre la funzione
, mentre la funzione 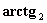 per
per 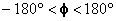 ; per esempio prendo un certo angolo che può assumere i valori
su tutto l’angolo giro; se
; per esempio prendo un certo angolo che può assumere i valori
su tutto l’angolo giro; se 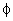 cade nel secondo e
terzo quadrante, ovvero per valori di
cade nel secondo e
terzo quadrante, ovvero per valori di 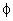 maggiori di più o
meno 90°, la funzione arctg classica
specularizza quell’angolo nel primo o secondo quadrante, mentre l’
maggiori di più o
meno 90°, la funzione arctg classica
specularizza quell’angolo nel primo o secondo quadrante, mentre l’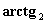 lo riporta correttamente a tutto l’angolo giro. Questo è
utile quando lo sfasamento tra pressione e velocità è tale da finire nel
secondo e terzo quadrante e dunque utilizzare l’
lo riporta correttamente a tutto l’angolo giro. Questo è
utile quando lo sfasamento tra pressione e velocità è tale da finire nel
secondo e terzo quadrante e dunque utilizzare l’ mi permette di non perdere informazione sull’angolo.
mi permette di non perdere informazione sull’angolo.
·
Prodotto
tra pressione e velocità:
Torniamo al nostro pistone che
spinge l’aria con la sua legge del moto; considero il caso particolarmente
semplice di segnali sinusoidali e suppongo che sulla pelle del pistone
pressione e velocità siano in fase fra loro: se impongo una velocità al
pistone, il sistema reagisce con una proporzionale pressione.
Calcolo l’energia sonora E
[J(Joule)] che sto cedendo al campo acustico:
 (24)
(24)
dove
A = area del
pistone
p = pressione
X = spostamento;
e la potenza acustica [W(Watt)]:
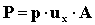 . (25)
. (25)
Dunque una sorgente sonora è
caratterizzata dall’energia sonora che è in grado di irradiare nell’unità di
tempo, altrimenti detta potenza acustica e che rappresenta una parte molto
piccola della potenza globale posseduta, normalmente meccanica e termica.
Nel caso di una sorgente di
ridotte dimensioni (puntiforme) ed omnidirezionale (sorgente che emette in
tutte le direzioni) posta in un mezzo (aria) isotropo, che presenta cioè la stessa resistenza in ogni punto,
l’energia si irradia nello spazio circostante in modo uniforme al variare della
direzione; si avrà quindi una propagazione (campo acustico attivo) per onde sferiche. Misurando la variazione
della pressione atmosferica causata dalla “perturbazione”, si noterà che essa
diminuisce di ampiezza man mano che ci si allontana dalla sorgente perché
l’energia si distribuisce su una superficie sempre maggiore (fronte d’onda) di emissione.
In una posizione qualsiasi
dello spazio si può allora descrivere il campo acustico con una grandezza
caratterizzata da direzione, verso ed ampiezza (vettore), che rappresenti la
quantità di energia che fluisce attraverso l’unità di superficie. Questa
caratteristica è detta intensità del
campo acustico ed è una grandezza estremamente importante, anche se quella
che viene più comunemente misurata in acustica è la pressione acustica (misura fonometrica) in quanto la variazione di
pressione atmosferica è una quantità relativamente semplice da rilevare.

Figura 21 – Intensità di una sorgente sonora attraverso una superficie
Formalmente si definisce il
vettore intensità sonora o acustica 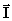 come il prodotto
della variazione di pressione p per
la velocità di oscillazione u delle
particelle costituenti un ipotetico elemento d’aria:
come il prodotto
della variazione di pressione p per
la velocità di oscillazione u delle
particelle costituenti un ipotetico elemento d’aria:
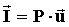 (26)
(26)
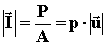 (27)
(27)
(essendo
una potenza acustica su superficie, è misurata in [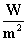 ]).
]).
Nel caso più generico di forme
d’onda non perfettamente sinusoidali e non in fase, il concetto rimane vero
localmente, ovvero istante per istante il prodotto tra il valore istantaneo
della pressione e della velocità produce la cosiddetta intensità istantanea i, che può assumere valori
alternativamente positivi o negativi:
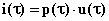 (28)
(28)
Nel caso delle due sinusoidi sfasate (un caso ancora relativamente semplice), l’intensità istantanea
oscilla con frequenza doppia dei segnali di partenza.
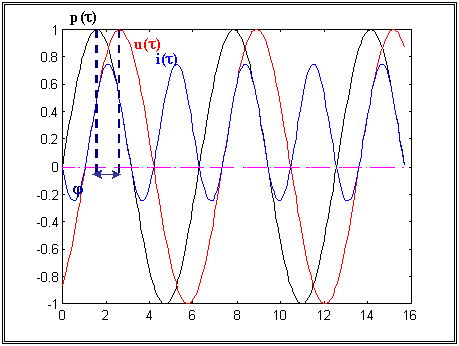
Figura 22
In presenza di segnali
complessi con più sinusoidi sovrapposte l’intensità istantanea assume valori
senza senso; tuttavia, se faccio una media nel tempo dell’intensità istantanea
ritrovo comunque l’intensità media 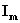 , che mantiene un significato fisico importante:
, che mantiene un significato fisico importante:
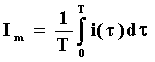 (29)
(29)
mi dice, integrando sul tempo T (che nel caso di segnali periodici
coincide con il periodo, mentre se
il segnale è aperiodico rappresenta il
tempo di vita dell’oscillazione). Ottengo dunque un’informazione energetica
che ha un significato: è l’energia che si è trasferita attraverso il mio
sistema; stiamo parlando di un sistema di propagazione che trasporta energia e dunque
c’è un flusso di energia che attraversa il tubo (anche se localmente tale
flusso può oscillare in maniera bizzarra). Lasciando esaurire l’oscillazione
trovo un trasferimento di energia netto che è passato lungo il tubo: non si
tratta di un sistema conservativo in cui l’energia è intrappolata in un canale,
ma è un sistema che travasa energia: entra energia a sinistra ed esce a destra
come un conduttore elettrico (il paragone continua: il tubo assomiglia a un
filo percorso da corrente elettrica alternata che porta un segnale elettrico e
dunque potenza elettrica, ma questo è un caso particolare perché c’è una sola
eccitazione elettrica di tipo sinusoidale, non vi sono forme d’onda strane o
fenomeni complessi di più frequenze – le correnti elettriche nei circuiti
viaggiano a 50 Hz e basta). Nel caso delle correnti elettriche questo integrale
si risolve dando il risultato noto:
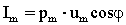 (30)
(30)
dove 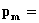 pressione media
pressione media
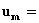 velocità
media
velocità
media
 angolo di
sfasamento
angolo di
sfasamento
e può
essere applicato al caso acustico supponendo però di avere una sola frequenza
in una guida d’onda che trasmette il segnale senza dispersione di energia
(assenza di fenomeni di attenuazione). Il caso limite si ha quando lo
sfasamento è di 90°, perché in questa situazione non c’è più trasporto di
energia: l’energia oscilla avanti e indietro, ma le aree positive pareggiano le
aree negative e quindi siamo in presenza di un’onda stazionaria, ovvero di un
sistema che sta oscillando senza più trasportare energia.
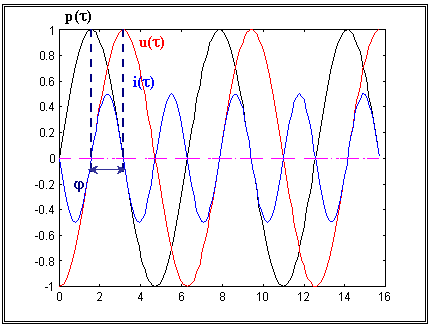
Figura 24
La relazione tra potenza e
intensità è insita nella definizione di quest’ultima: “potenza su unità di
superficie”; è quindi possibile determinare la potenza emessa da una o più sorgenti
poste all’interno di una superficie chiusa, integrando nello spazio l’intensità
misurata sulla superficie:
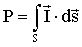 (31)
(31)
Mentre la relazione potenza – intensità è valida in
qualsiasi tipo di campo acustico, non è invece derivabile un’espressione
diretta che leghi potenza – potenza salvo che per il caso del “campo libero”.
Per capirne la problematica si deve prestare attenzione al fatto che mentre l’intensità rappresenta molto
semplicemente la potenza acustica di una sorgente distribuita sulla superficie
di emissione, la pressione è una
conseguenza di un fenomeno vibrazionale e dipende dalla potenza acustica della sorgente, dalla direzionalità dell’emissione, dall’ambiente circostante, e varie altre situazioni al contorno.
L’analogia del “discorso acustico” potrebbe essere fatta
con quello termico: una stufa elettrica è una sorgente di potenza termica in
grado di riscaldare un ambiente, ed il “grado” di riscaldamento viene misurato
con una misura di temperatura; la stessa stufa posta in un altro ambiente
mantiene la stessa potenza termica, ma la temperatura di quest’altro ambiente
non sarà necessariamente la stessa del precedente, in quanto intervengono
fattori come il volume dell’ambiente e il grado di isolamento termico delle pareti.
La misura della temperatura è infatti corrispondente alla misura di pressione
acustica: essa dipende dal volume dell’ambiente e dalle caratteristiche
fonoassorbenti delle pareti che lo delimitano.
La relazione precedente rimane valida anche se la sorgente
che irradia energia acustica, posta all’interno della superficie, non ha
un’emissione isotropica (omnidirezionale), come anche nel caso in cui la
superficie di misura non ha una forma regolare. Nel caso semplice di una
emissione per onde sferiche, si ricava l’intensità della potenza attraverso la
superficie di emissione:
 , (32)
, (32)
che permette di comprendere
come l’intensità sonora di una sorgente non sia costante ma vari a seconda
della distanza da quest’ultima, in virtù della dipendenza da r.
La determinazione della potenza
acustica richiede il calcolo dell’integrale di superficie della componente
dell’intensità perpendicolare ad una superficie di misura racchiudente la
sorgente: 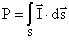 . L’accuratezza di questo tipo di misura è limitata da tre
fattori:
. L’accuratezza di questo tipo di misura è limitata da tre
fattori:
·
l’accuratezza della stima della componente normale di
intensità;
·
la precisione dell’integrazione;
·
la stazionarietà della sorgente e del rumore di fondo
durante la misura.
La
precisione nella misura della componente del vettore intensità è limitata da
due tipi di errore: quello sistematico
e quello casuale. Gli errori casuali
possono essere eliminati usando un tempo di mediazione sufficientemente lungo.
Nell’intervallo utile di frequenze di un analizzatore di intensità,
caratterizzato da buone proprietà direzionali, gli errori sistematici sono
predominanti a causa di disaccoppiamenti di fase tra i canali di misura.
La precisione dell’integrazione dipende dalla complessità
del campo sonoro sulla superficie di misura, dalle dimensioni dei segmenti e
dal tipo di tecnica usata per stimare la componente normale di intensità
associata ad ogni segmento.
Le due tecniche di misura più usate sono in genere quella
a punti (definita dalla normativa
ISO 9614) e quella a scansione,
quest’ultima generalmente più rapida e più pratica.
La misura a scansione si effettua con un tempo di media
sufficientemente lungo per poter eseguire una scansione completa dell’elemento
di superficie, come se si dovesse verniciarlo con un pennello. Quello che si
ottiene è un singolo valore medio dell’intensità nello spazio che, moltiplicato
per l’area della superficie, dà il valore della potenza acustica attraverso
l’area dell’elemento considerato; sommando poi i valori di ogni singola
superficie si ottiene la potenza acustica totale. Se la sonda è usata a mano,
essa richiede un operatore esperto e deve essere mossa a velocità costante. Con
la tecnica a scansione non è possibile riportare esattamente che cosa è stato
fatto nella misura e vengono perse le informazioni dettagliate riguardo al
campo sonoro sulla superficie di misura, anche se è spesso più precisa da un
punto di vista matematico perché si avvicina di più all’integrale continuo
nello spazio.
La tecnica per punti richiede in genere un tempo più
lungo, ma è possibile un’esatta descrizione della procedura usata e la misura
dei valori in ogni posizione rende possibile una stima della precisione; per
questo motivo le attuali stesure di normative ISO in materia permettono solo
quest’ultimo tipo di misura.

![]() ,
, ![]() ,
, ![]()
![]() ,
,