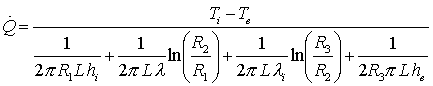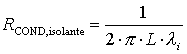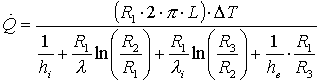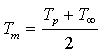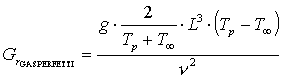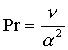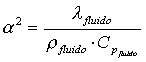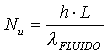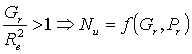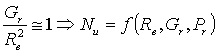In questa
lezione saranno trattati i seguenti argomenti:
·
Raggio critico
all’isolante
·
Applicazioni su
potenza termica e raggio critico all’isolante
·
Calcolo dei
coefficienti di convezione
Raggio
critico all’isolante.
Cerchiamo di calcolare la
potenza termica dispersa da una tubazione.
A tal fine consideriamo
un tubo d’acqua calda che normalmente disperde calore dall’interno del tubo
stesso verso l’esterno, come indicato in fig.1 dalle frecce rosse. La
temperatura del liquido all’interno del tubo Ti è maggiore della temperatura esterna Te . Supponiamo inoltre che
all’interno del tubo ci sia un coefficiente di convezione hi diverso dal coefficiente di convezione esterno he .

Supponendo che non siano
presenti fenomeni di irraggiamento, questo calo di temperatura può essere visto
come una serie di 3 resistenze, come mostrato in figura:

Fig.2
Abbiamo infatti una
resistenza di convezione interna seguita da una resistenza di conduzione e da
una di convezione esterna. I 3 resistori risultano essere “in serie” in quanto
il calore viene ceduto dal liquido alla parete interna del tubo, che si troverà
a una temperatura Tpi, da
quest’ultima alla parete esterna del tubo, sulla quale misureremo una
temperatura Tpe, e da qui il calore
viene infine ceduto all’ambiente esterno.
Vediamo ora come è
possibile descrivere il fenomeno dal punto di vista dello scambio termico:
Sappiamo che vale sempre
la relazione:
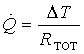 (1)
(1)
Nel nostro caso la
resistenza totale è ottenuta dalla somma delle 3 resistenze RCONV , i , RCOND e RCONV , e in quanto sono collegate “in serie”.
![]() (2)
(2)
Ognuna di esse può essere
determinata come segue:
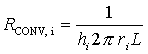 (3)
(3)
dove ri indica il raggio interno del tubo e L la sua lunghezza;
 (4)
(4)
dove l indica la conducibilità del materiale di cui è
costituito il tubo, ri e re indicano il raggio
interno ed esterno di quest’ultimo;
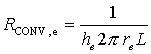 (5)
(5)
dove re indica il raggio esterno del tubo e L la sua lunghezza.
Quindi l’equazione (1)
risulta:
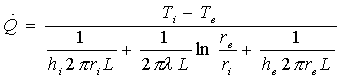 (6)
(6)
che può essere sviluppata
con semplici operazioni algebriche nella forma:
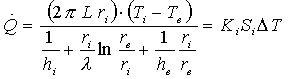 (7)
(7)
dove ![]() indica la superficie
di scambio.
indica la superficie
di scambio.
Ki
è detto coefficiente globale di scambio termico.
In realtà tale
definizione non è del tutto precisa (e ormai non appartiene più alla
terminologia tecnica dell’ingegnere) in quanto un coefficiente dovrebbe essere
una quantità adimensionale.
Ecco allora che viene
introdotta una nuova quantità CT
chiamata: conduttanza termica specifica, cosi definita:
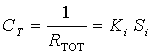 (8)
(8)
dove ![]() indica la superficie
di scambio.
indica la superficie
di scambio.
Ecco allora che abbiamo
capito quanto vale la potenza termica dispersa da una tubazione.
Vediamo ora un esempio
pratico per fissare meglio i concetti appena trattati.
Esempio.
Prendiamo in esame un
tubo di polietilene (plastica) e supponiamo di conoscere il suo raggio interno
ed esterno, la sua lunghezza, il coefficiente di convezione interno ed esterno
e la temperatura all’interno del tubo stesso e quella dell’ambiente esterno:
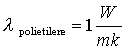
![]()
![]()
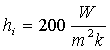

![]()
![]()
![]()
Utilizzando la relazione
(7) determinata in precedenza e facendo una mera sostituzione, otteniamo:
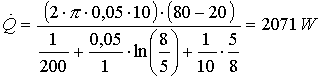
Quindi possiamo affermare
che un tubo di 10 metri contenente acqua calda, per esempio quelli che portano
il riscaldamento nelle nostre case, ha una potenza termica dispersa di ben 2071
W!! Ricordiamo che per scaldare una casa, indicativamente sono necessarie
alcune migliaia di Watt, quindi se il tubo che porta l’acqua del riscaldamento
disperde di per se più di 2000 W in 10 metri diventa ininfluente l’utilizzo di
un corpo scaldante! (pompe di calori o simili).
Vediamo allora come sia
possibile ovviare a questo problema ricoprendo il tubo con un materiale
isolante (in giallo in fig.3 e 4):

Il risultato è quello di
avere un secondo tubo di materiale isolante che ricopre quello di partenza,
come illustrato nella figura seguente:
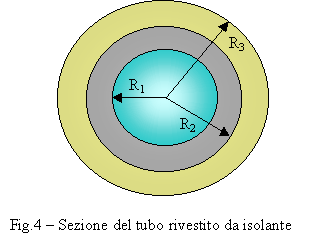
R1 rappresenta il raggio interno del tubo, R2 il suo raggio esterno e R3 il raggio esterno del tubo isolante.
Supponendo sempre che non
siano presenti fenomeni di irraggiamento, il sistema viene ora rappresentato da
4 resistenze poste “in serie”. Rispetto al modello di fig.2 dobbiamo infatti
aggiungere la resistenza di conduzione dovuta alla presenza del materiale
isolante:
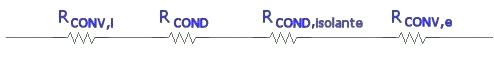
Tenendo presente che i dati del problema non sono cambiati rispetto a prima dove non avevamo preso in considerazione l’isolante e che R1 = ri e R2 = re, sostituiamo nella (11) tali dati ottenendo:
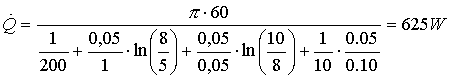
Ecco allora che
rivestendo il tubo di partenza contenente acqua calda con uno di poliuretano
espanso abbiamo ottenuto una dispersione di calore molto minore, pari quasi a
un quarto del precedente.
Riguardo a questo versatile
isolante, rimandiamo ai siti internet:
·
http://www.politop.it/EPS.htm
·
http://www.spazioambiente.com/alveo.htm#resterm
per avere qualche informazione
in più e qualche curiosità.
Utilizzare un materiale
isolante non sempre però riduce lo scambio termico.
Questo effetto
indesiderato si può ottenere per esempio rivestendo il tubo originario con una
guaina sottile, caratterizzata da un’alta conucibilità termica.
In generale ciò dipende
da vari fattori. Vediamoli meglio in dettaglio:
Consideriamo la relazione
(11). Al denominatore abbiamo i seguenti addendi:
A = ![]() (12)
(12)
B = 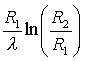 (13)
(13)
C = 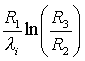 (14)
(14)
D =  (15)
(15)
A e B sono costanti che non dipendono dalla
geometria e dal tipo del materiale isolante scelto.
All’aumentare del raggio
esterno (R3)
dell’isolante, C aumenta e allo
stesso tempo D diminuisce. Per
ottenere uno scambio termico ridotto è necessario che il denominatore della
(11) sia il più grande possibile, quindi in generale l’aumento di C deve prevalere sulla diminuzione di D. Questo dipende dalle 2 costanti che
precedono i due addendi C e D:
c = ![]() (16)
(16)
d = ![]() (17)
(17)
Le costanti c e d dipendono rispettivamente dalla conducibilità termica
dell’isolante li e dal coefficiente di convezione esterno he.
Quindi in base al valore di quest’ultimo si dovrà scegliere opportunamente il raggio del tubo isolante e il materiale di cui è composto.
A tal proposito mostriamo
qui di seguito una tabella dei coefficienti di conducibilità termica dei
materiali più comuni.
Come si può notare la
conducibilità termica varia a seconda della temperatura.
In generale essa misura l'attitudine di una data sostanza (non solo solida
ma anche liquida o gassosa) a trasmettere calore per conduzione; corrisponde al
valore che può assumere in un dato intervallo di temperatura il flusso termico
che lambisce la superficie di misura, sotto l’effetto della caduta di
temperatura in direzione perpendicolare alla superficie.
|
|
TEMPERATURA |
||||
|
MATERIALI |
0°C |
50°C |
100°C |
150°C |
200°C |
|
Acqua |
0.54 |
|
|
|
|
|
Alluminio |
178 |
|
|
|
|
|
Asfalto |
0.55 |
|
|
|
|
|
Basalto |
1.1 |
2.4 |
|
|
|
|
Calcestruzzo |
0.7 |
1.2 |
|
|
|
|
Cartone |
0.12 |
0.25 |
|
|
|
|
Cemento |
0.8 |
1.10 |
|
|
|
|
Ferro e acciaio |
40 |
50 |
|
|
|
|
Fibre di vetro |
0.028 |
0.032 |
0.036 |
0.045 |
0.055 |
|
Fibre di amianto |
0.045 |
0.045 |
0.048 |
0.058 |
0.070 |
|
Gesso |
0.4 |
0.6 |
|
|
|
|
Ghiaccio |
1.9 |
|
|
|
|
|
Granito |
2.7 |
3.5 |
|
|
|
|
Lane minerali |
0.030 |
0.035 |
0.040 |
0.047 |
0.057 |
|
Linoleum |
0.16 |
|
|
|
|
|
Marmo |
1.8 |
3 |
|
|
|
|
Mattoni pieni |
0.6 |
0.9 |
|
|
|
|
Mattoni forati |
0.3 |
0.7 |
|
|
|
|
Muratura di pietrame |
1.2 |
2.1 |
|
|
|
|
Pietra arenaria |
1.1 |
1.5 |
|
|
|
|
Pietra calcarea |
0.6 |
0.8 |
|
|
|
|
Piombo |
30 |
|
|
|
|
|
Polistirolo espanso |
0.028 |
|
|
|
|
|
Poliuretano espanso |
0.020 |
|
|
|
|
|
Prodotti a base d
magnesia |
0.040 |
0.045 |
0.052 |
0.057 |
0.063 |
|
Quercia |
0.18 |
0.22 |
|
|
|
|
Resine fenoliche
espanse |
0.030 |
|
|
|
|
|
Sabbia asciutta |
0.28 |
|
|
|
|
|
Sugheri |
0.040 |
0.050 |
|
|
|
|
Vetro |
0.4 |
0.8 |
|
|
|
|
Vetro cellulare espanso |
0.046 |
|
|
|
|
Tabella 1 – Coefficiente di conducibilità termica per alcuni materiali in![]()
Ma come si spiega il
fatto che utilizzando un materiale isolante si ottiene un aumento dello scambio
termico con l’esterno?
Questo apparente
paradosso può essere chiarito dal grafico seguente:

Fig.6
All’aumentare di R3 la resistenza totale RTOT diminuisce fino a
quando non si arriva al cosidetto raggio critico RC. Nel tratto di curva appena descritto si ottiene
quindi un aumento dello scambio termico rispetto al mancato impiego di un
isolante, in quanto diminuendo RTOT
possiamo notare dalla (1) che ![]() aumenta. Superato questo punto RTOT incomincia ad aumentare
fino a raggiungere il valore iniziale, per R3
= RL .
aumenta. Superato questo punto RTOT incomincia ad aumentare
fino a raggiungere il valore iniziale, per R3
= RL .
Se aumentiamo ancora il
raggio esterno del tubo isolante otteniamo un’aumento pronunciato della
resistenza totale, superando abbondantemente il suo valore iniziale, e facendo
quindi diminuire drasticamente lo scambio termico.
Se quindi il raggio del
tubo da isolare è maggiore di RC
rivestendolo con un tubo per esempio di polietilene si ottiene sicuramente una
diminuzione dello scambio termico con l’esterno, indipendentemente dalla misura
del raggio dell’isolante.
Determiniamo ora RC dal punto di vista
analitico. Esso è il punto di minimo della relazione (11), quindi per
determinarlo è sufficiente derivare tale funzione rispetto ad R3. Notiamo anzitutto che
gli unici termini in cui compare R3
sono gli addendi C e D al denominatore, i soli che derivati
risultano essere diversi da zero.
Ponendo la derivata
uguale a zero:
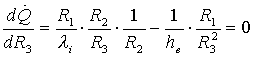 (18)
(18)
Da cui otteniamo:
 (19)
(19)
Nell’esercizio svolto in
precedenza risulta essere :
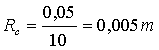
Avendo infatti scelto un
raggio dell’isolante maggiore del raggio critico abbiamo inibito lo scambio
termico.
Esercizio.
Prendiamo in
considerazione un filo elettrico di diametro 1mm e lungo un metro.
Supponiamo di farlo percorrere
da una corrente di 10A e cerchiamo di valutare, in base al calore scambiato con
l’ambiente esterno, la temperatura raggiunta dal filo stesso.
Sarà conveniente
rivestirlo con una guaina?
Quali effetti otterremmo?
Fig.7
Vediamo meglio i dati del
problema:
![]() - Diametro del filo
- Diametro del filo
![]() - Resistenza specifica del filo
- Resistenza specifica del filo
![]() - Corrente elettrica che
percorre il filo
- Corrente elettrica che
percorre il filo
![]() - Temperatura esterna
- Temperatura esterna
![]() -
Coefficiente di convezione esterno
-
Coefficiente di convezione esterno
Il passaggio di corrente
nel filo produce un calore:
![]() (20)
(20)
che può essere
determinato anche secondo la formula:
![]() (21)
(21)
Sapendo inoltre che:
![]() (22)
(22)
Posso ricavare dalla (20)
la temperatura del filo:
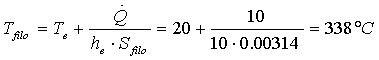 (23)
(23)
che è sicuramente un
valore inaccettabile in quanto troppo elevato.
Proviamo allora a
rivestire il filo con una guaina isolante di plastica (![]() ) come mostrato in
figura:
) come mostrato in
figura:
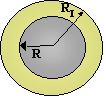
Fig.8 – Sezione del filo rivestito da isolante
Calcoliamo il raggio
critico, in modo da scegliere il raggio migliore per il nostro isolante:
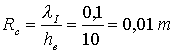
Utilizzando la (1) nella
forma della (7), possiamo calcolare lo scambio termico:
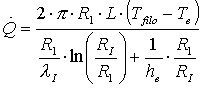 (24)
(24)
da cui possiamo ricavare
la temperatura del filo:
 (25)
(25)
sostituendo ora tutti i
valori, compresi quelli determinati in precedenza, otteniamo che:
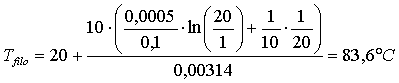 (26)
(26)
Possiamo concludere che è
sicuramente vantaggioso rivestire il filo con una guaina in plastica, in quanto
segue un abbassamento della temperatura del filo notevole, pari a ben 254.4°C.
Rifacendo i calcoli con
un raggio dell’isolante maggiormente proporzionato al raggio del tubo (RI = 2mm) la temperatura del
filo scende a 190.3 °C, che è comunque un valore più che accettabile, rispetto
ai 338 °C del filo non isolato.
I problemi di
dissipazione termica sono molto importanti soprattutto nella progettazione e nella
costruzione dei microprocessori per computer.
Infatti le prestazioni di
questi ultimi vengono decisamente penalizzate dal loro aumento di temperatura,
che può variare da una decina di gradi a quasi 50 gradi nel caso in cui i
dissipatori di calore, collocati a contatto con il processore, siano stati
montati in maniera errata.
Oltre ad un calo notevole
di prestazioni, ciò può provocare anche il danneggiamento irreparabile del
processore, che in certi casi deve essere sostituito.
E’ stato calcolato che un PC mal aerato può perdere da subito circa il 20% delle proprie capacità e poi arrivare a continui blocchi e spegnimenti.
Per evitare ciò, vengono
fatti studi accurati sulla geometria delle “alette” dei dissipatori, a seconda
della marca e del tipo del processore.

Fig.8 – Dissipatore con ventola
Per facilitare la
dissipazione di calore vengono inoltre montate ventole per allontanare il più
rapidamente possibile aria calda dal processore, e permettergli di lavorare in
un ambiente caratterizzato da un costante ricambio d’aria (vedi fig.8).
Ma non distacchiamoci troppo dagli argomenti che caratterizzano il corso, e lasciamo al lettore la possibilità di approfondire tale argomenti con alcuni link interessanti:
·
http://www.hardwaretips.com/overclock/over03.htm
·
http://www.hwmaniac.com/Archivio/comparazione_dissi_rame/index3.shtml
·
http://www.vincenzov.net/tutorial/dissipatori/dissipatori.htm
·
http://digilander.iol.it/Marino5/cool1.htm
Calcolo
dei coefficienti di convezione:
Cercheremo ora di
stabilire la metodologia per calcolare i coefficienti di convezione dentro un
fluido (che può essere aria o acqua). I risultati ottenuti potranno poi
estendersi in ambito più generale a tutti i tipi di fluidi, grazie al concetto
di analogia di Reynolds, già visto in precedenza.
Possiamo quindi
determinare il fattore di attrito, sfruttando anche gli argomenti trattati in
fluidodinamica:
 (27)
(27)
dove Re è il numero di Reynolds, e ![]() è il cosiddetto fattore di forma.
è il cosiddetto fattore di forma.
Importante è sottolineare
che il fattore di attrito x è una grandezza adimensionale, che la rende
quindi sempre utilizzabile con ogni unità di misura, senza essere suscettibile
a cambiamenti.
Questo stesso schema
logico viene applicato ai problemi di scambio termico per convezione.
Avremo quindi un
parametro adimensionale in uscita h*,
che si può intendere come la versione adimensionalizzata del coefficiente di
convezione h.
h* in
generale è definito come funzione di alcune entità adimensionali.
Il tutto risulterà più
chiaro dopo aver enunciato il seguente teorema, alla base dell’analisi
dimensionale:
Teorema di
Buckingham:
Un sistema descritto da n variabili, costituite mediante r dimensioni è anche descritto da n - r gruppi indipendenti privi di dimensioni fisiche.
Che possiamo riassumere
con la formula:
![]() (28)
(28)
In un problema di scambio
termico per convezione risulta:
![]()
Da cui deduciamo che h* è funzione di 4 raggruppamenti
adimensionali indipendenti.
In particolare:
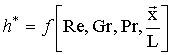 (29)
(29)
Vediamo in dettaglio i 4
numeri puri che mi caraterizzano h*:
Numero di Reynolds:
 (30)
(30)
dove:
W = velocità
media del flusso del fluido
L = lunghezza caratteristica
m = coefficiente di viscosità dinamica del fluido
Il numero di Reynolds
esprime il rapporto tra le forze d’inerzia e le forze viscose di un fluido.
A seconda del valore che
assume il moto di un fluido all’interno di un condotto cambia. Vediamo come:
-
Re < 2300 moto
del fluido laminare; (30.1)
-
Re > 4100 moto
del fluido turbolento. (30.2)
Numero di Grashof:
 (31)
(31)
dove:
g = accelerazione gravitazionale
b = coefficiente di dilatazione termica
L = lunghezza caratteristica
Tp = temperatura della parete del condotto
T∞ = temperatura esterna
n = viscosità
Il numero di Grashof Gr
è una grandezza fisica che mi rappresenta le forze di galleggiamento.
Tramite esso posso per
esempio stabilire matematicamente che l’aria calda galleggia su quella fredda.
Questa conclusione che
può sembrare banale, ha dato in passato numerosi problemi alle prime capsule
spaziali presurizzate in orbita intorno alla Terra.
Infatti per dissipare il
calore degli apparati elettronici di questi macchinari, erano state progettate
alette particolari collaudate con successo sul nostro pianeta, senza però tener
conto dell’assenza di gravità nello spazio!
Infatti dalla (31) si può
notare che Gr è direttamente proporzionale all’accelerazione
di gravità g.
Ecco allora che risulta
facile capire come l’aria calda non potesse galleggiare su quella fredda
soprastante, rimanendo intrappolata tra le alette, in quanto veniva a mancare
la componente di scambio termico per convezione naturale.
Quest’errore progettuale
ha causato fenomeni di surriscaldamento accentuati nei primi satelliti,
compromettendone il funzionamento.
Il coefficiente di
dilatazione termica b evidenzia
invece quanto si dilati il gas al variare della temperatura:
 (32)
(32)
In generale b varia al variare della temperatura. Sarà quindi opportuno risalire al
valore corretto utilizzando tabelle specifiche. Alcuni valori di b dei materiali più comuni sono mostrati in fig.9 alla pagina successiva.
EIANel caso dei gas perfetti, possiamo risalire all’espressione del
coefficiente di dilatazione termica ricordando che:
![]() (33)
(33)
da cui:
 (34)
(34)
derivando ora rispetto a T:
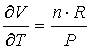 (35)
(35)
|
|
Coefficiente di
dilatazione termica
|
Materiale |
b ( ° C –1 ) |
|
Alluminio |
24 x 10 –6 |
|
Diamante |
1.3 x 10 –6 |
|
Ferro |
12 x 10 –6 |
|
Piombo |
29 x 10 –6 |
|
16 x 10 –6 |
|
|
Vetro |
9 x 10 –6 |
|
Zinco |
17 x 10 -6 |
|
Legno (abete) |
4 x 10-6 |
|
Mattone |
5 x 10-6 |
|
Pietra |
5 x 10-6 |
|
Stagno |
23 x 10-6 |
|
Calcestruzzo |
10 x 10-6 |
|
Calcestruzzo alleggerito |
8 x 10-6 |
|
Malta di calce |
8 x 10-6 |
n = viscosità cinematica
Definendo il numero di
Reynolds abbiamo già detto che esprime il rapporto tra le forze d’inerzia e le
forze viscose di un fluido:
 (44)
(44)
Analogamente possiamo
esprimere il numero di Grasof come:
 (45)
(45)
Se Gr
<< 1 le forze di galleggiamento sono molto meno rilevanti rispetto alle
forze viscose, ciò significa che siamo nella condizione di convezione forzata,
in quanto gli effetti di convezione naturale sono irrilevanti.
Per stabilire se siamo o
meno nella situazione di convezione forzata è però più rilevante monitorare il
rapporto:
![]() (46)
(46)