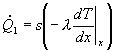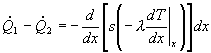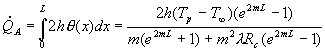SUPERFICI ALETTATE
INDICE
RAPIDO
Le
alette: Descrizione e Funzionamento
Studio matematico della dispersione
Calcolo dell'efficienza di una singola aletta
e dell'intero blocco di alette
Esercizio
- Alettatura su una CPU
Cosa sono e dove si impiegano.
In molti dispositivi
elettronici attuali è molto importante il controllo della temperatura di
esercizio al fine di non comprometterne il funzionamento, per questo è
necessario rendere ottimale lo smaltimento del calore.
Per aumentare lo scambio
termico e quindi evitare il surriscaldamento di transistors, chips e altri
dispositivi elettronici si possono utilizzare due metodi:
·
applicare superfici
alettate
·
forzare l’aria sul dispositivo. (es. ventola).
Il primo metodo essendo
poco costoso e facilmente realizzabile è il migliore per aumentare i
coefficienti di convezione dispositivo aria e di conseguenza lo smaltimento del
calore.
Il secondo come vedremo
in seguito si trova accoppiato al primo come aiuto, da solo infatti produce
quasi irrilevanti effetti di raffreddamento e per contro spinge le particele
presenti nell’aria a toccare il dispositivo che se incandescente le carbonizza.
Si può comprendere l’importanza che ha
assunto lo studio dell’alettatura soprattutto nel raffreddamento delle CPU (non
esiste processore che non possieda la sua coppia ventola-dissipatore) e di
tutti gli altri dispositivi che fanno impiego dell’elettronica e della
microelettronica.
Le alette.
Descrizione.
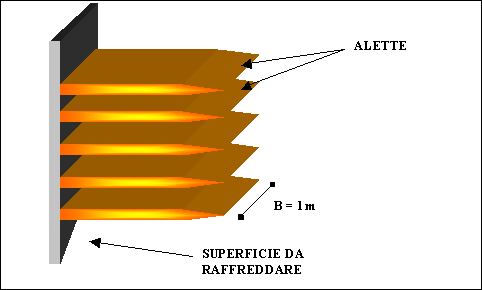
Le alette sono dei
parallelepipedi, di materiale metallico, posti con la faccia più piccola a
contatto con la superficie da raffreddare (Fig. 1), in
sostanza possono essere viste come una serie di "costole"
rettangolari che sporgono perpendicolarmente dalla superficie da raffreddare,
Sono costituite di materiale metallico in genere Alluminio o Oro (come è facile
intuire per motivi di costo e duttilità il primo è il più utilizzato).
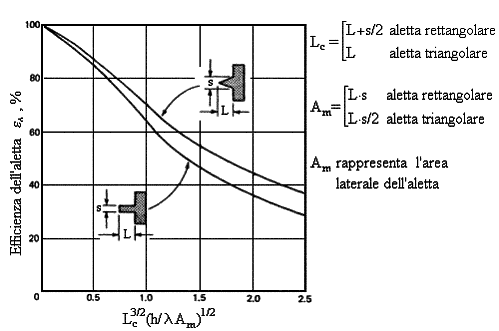
Esistono alette di svariate forme che permettono di migliorarne le prestazioni: a sezione rettangolare (quelle in Fig.1, costituiranno il nostro modello), coniche, a spillo, circolari e molte altre che qui non tratteremo. A pagina 9 sono riportate due tabelle che forniscono il rendimento delle alette in base alle loro rispettive forme.
Fig. 1 – Superficie alettata.
Funzionamento.
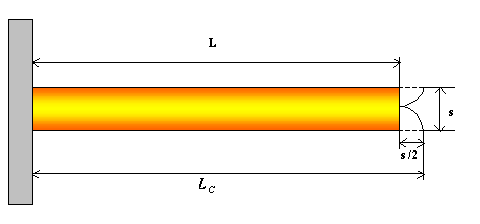
Parametri geometrici
caratteristici di un’aletta, considerata separatamente dalle altre, sono
(Fig.2):
·
la lunghezza L
·
lo spessore s
·
per quanto riguarda
la terza dimensione, cioè la profondità dell’aletta noi la considereremo
unitaria (1 metro), potendola anche porre infinita.

Fig. 2 – Aletta.
Il calore per conduzione fluisce dal dispositivo da raffreddare al metallo delle alette, per poi essere disperso per convezione tramite le due facce, inferiore e superiore, ed in misura minore dalla testa delle stesse.
Nel caso in cui l’aletta
sia stata ottenuta per fusione dal dispositivo, nel punto di contatto entrambi
avranno la stessa temperatura che indicheremo con TP (temperatura
di parete), spostandoci lungo l’aletta, la temperatura tenderà a diminuire fino
al valore di temperatura dell’ambiente circostante (normalmente rappresentato
dall’aria) che indicheremo con ![]() . In figura 3 è
possibile vedere rappresentato graficamente il flusso del calore attraverso
l’aletta. Le linee scure rappresentano il calore che dal dispositivo da
raffreddare fluiscono nell’aletta per poi essere disperso dalle facce laterali
in maniera variabile con la posizione lungo la sezione.
. In figura 3 è
possibile vedere rappresentato graficamente il flusso del calore attraverso
l’aletta. Le linee scure rappresentano il calore che dal dispositivo da
raffreddare fluiscono nell’aletta per poi essere disperso dalle facce laterali
in maniera variabile con la posizione lungo la sezione.
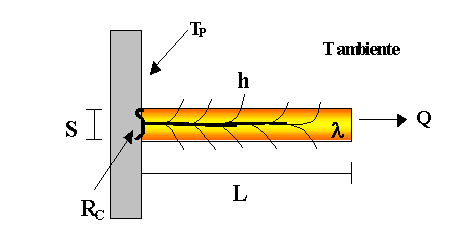
Fig. 3 – Sezione trasversale aletta.
OSS: Nel caso in cui, invece, l’aletta sia stata
applicata successivamente alla costruzione del dispositivo, bisognerà tenere
conto di una certa resistenza RC
nel punto di contatto col dispositivo. In tal caso la temperatura alla base
dell’aletta sarà inferiore a TP
. Soluzione del problema è il tappetino termoconduttivo.
In figura 4 si può
notare, invece, l’andamento della temperatura in funzione della
lunghezza dell’aletta, si vede che esiste un punto oltre il quale lo scambio di
calore è pressoché nullo essendo la temperatura dell’aletta di poco superiore a
quella dell’ambiente, ![]() .
.
Fig. 4 – Temperatura dell’aletta in funzione della sua lunghezza.
Studio
matematico della dispersione.
Nello studio matematico
del funzionamento dell’aletta è necessario supporre che la propagazione del
calore nell’aletta avvenga solo lungo la componente parallela ad essa, in
realtà il calore si disperde anche sulle due facce laterali, ma se lo spessore
è trascurabile rispetto alla lunghezza dell’aletta (s<<L)
l’ipotesi fatta è accettabile.
Lungo la direzione delle
ascisse x, la resistenza termica R non è trascurabile, ma se
consideriamo un elemento infinitesimo dx possiamo su di esso supporla
costante, così come la temperatura T.
In Fig.5 si può notare
quale sia il computo del calore scambiato nell’elemento infinitesimo.
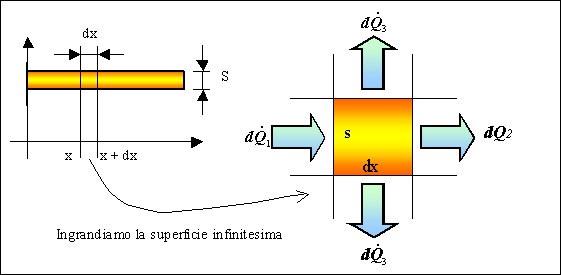 Fig. 5
– Analisi del calore scambiato da un elemento infinitesimo.
Fig. 5
– Analisi del calore scambiato da un elemento infinitesimo.
d![]() e d
e d![]() rappresentano le
potenze scambiate per conduzione, mentre
rappresentano le
potenze scambiate per conduzione, mentre ![]() rappresenta la potenza scambiata per
convezione. Supponiamo che quest’ultima assuma lo stesso valore sia
relativamente alla superficie superiore che a quella inferiore.
rappresenta la potenza scambiata per
convezione. Supponiamo che quest’ultima assuma lo stesso valore sia
relativamente alla superficie superiore che a quella inferiore.
Bilanciando gli scambi
abbiamo che:
POTENZA ENTRANTE = POTENZA USCENTE (1)
![]() (2)
(2)
·
Per x = 0 imponiamo
il valore della temperatura alla base dell’aletta. Per farlo dobbiamo tenere
conto del fatto che il dispositivo si trova alla temperatura Tp e che
fra esso e la base dell’aletta esiste una resistenza Rc.
Fig. 6
– Metodo grafico per calcolare di Lc
Procedendo in questo modo
è come se avessimo spaccato in due la punta dell’aletta e l’avessimo aperta in
modo da prolungare la superficie della stessa.
Le condizioni al contorno
dunque diventano:
![]() (16)
(16)
dove ![]() e
e ![]() .
.
Risolvendo otteniamo la A
e la B dell’ espressione (14):
Efficienza dell’alettatura.
Efficienza della singola aletta.
Consideriamo da prima il
caso della singola aletta e vediamo come calcolarne l’efficienza.
La potenza scambiata
dall’aletta è inferiore a quella scambiata se la stessa scambiasse calore
isotermicamente. Vediamolo meglio introducendo l’efficienza dell’aletta:
![]() (21)
(21)
Efficienza
di un blocco di alette.
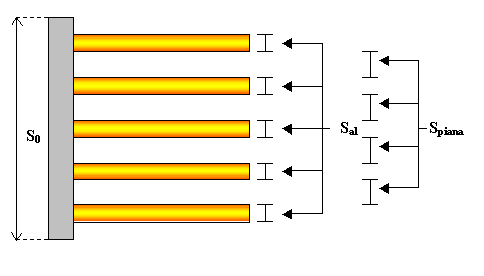
Fig. 7 – Vista in sezione di un’alettatura.
Fig. 8 – Grafico efficienza delle alette triangolari e rettangolari.
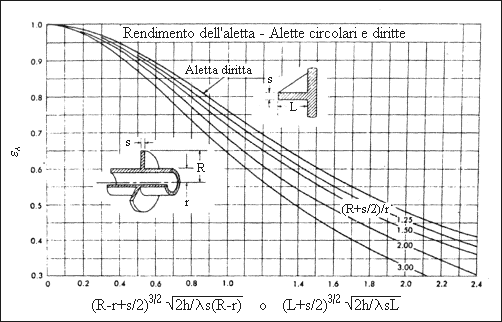
Fig. 9 – Grafico efficienza alette circolari e dritte.
Dimensionamento alettatura.
Ai fini pratici ciò che è
importante è la capacità di dimensionare un’alettatura su di un dispositivo in
base alle sue caratteristiche.
Per questo riportiamo qui
di seguito il metodo di dimensionamento, tenendo presente che si tratta di un
metodo tipicamente “controintuitivo”, cioè alla fine dei conti si vedrà
che è sempre meglio tenere le alette basse e poco spesse, contro quanto
l’intuizione suggerirebbe.
Se indichiamo con eal efficienza
della singola aletta e con etot l’efficienza totale dell’ alettatura è:
![]() (26)
(26)
dove si è posto:
![]()
![]()
da cui si ottiene finalmente:
![]()
ESERCIZIO
Alettatura su una CPU (Central
Processing Unit).
Oggigiorno lo studio del
raffreddamento dei processori dei PC ha assunto una importanza enorme, con CPU
che lavorano a frequenze sempre più elevate e vengono alimentate con tensioni
sempre maggiori per elaborare sempre più informazioni nel minor tempo
possibile.
Oltre alle CPU nei
computer di oggi anche il processore della scheda grafica così come i vari
chipsets presenti sulla scheda madre e sulle schede delle periferiche sono
dotati di dispositivi di raffreddamento.
Consideriamo una CPU (es.
PENTIUM PRO, Fig. 10) di un Computer con la superficie quadrata di lato L
= 50mm, tale dispositivo è in grado di dissipare una potenza di 50W
nell’ambiente (alla temperatura di 20 gradi Centigradi).

Fig. 10 – CPU (Central Processing Unit)
1.
Trovare a che
temperatura si porta il dispositivo.
2.
Studiare una
opportuna alettatura per abbassare la temperatura.
CASO A - Nessuna alettatura:
Risolviamo da prima il problema in situazione di convezione naturale, cioè in ambiente con aria ferma.
C’è solo scambio termico, quindi la potenza scambiata è:
![]() (1)
(1)
da cui:
![]() (2)
(2)
Supponiamo accettabile per la CPU una temperatura di 100°C.
E’ necessario a questo
punto conoscere il numero di Grashof Gr, la cui espressione è
data da:
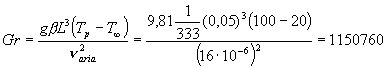
g = 9.81m/s2 è l’accelerazione di gravità
b = 1/T è il coefficiente di dilatazione termica (che nel caso di gas è l'inverso della temperatura).
L = 0.05m è il lato della superficie quadrata
naria = 16.10-6m2/s è la viscosità cinematica dell’aria
Il numero di Prandtl in
queste condizioni è Pr = 0,71
Possiamo, dunque,
calcolare il numero di Rayleigh Ra:
![]()
il valore ottenuto è
molto inferiore a 10⁹ quindi
ci troviamo in condizioni di moto laminare.
Valutiamo, ora, il numero
di Nusselt:
![]()
ma:
![]()
con laria = 0,03 w/mK è la conducibilità
termica dell’aria.
Ricaviamo dunque h:
![]()
Possiamo calcolare la temperatura del dispositivo:
![]()
Un valore che è decisamente troppo alto.
Nella trattazione
precedente, però, è stato trascurato lo scambio termico dovuto
all’irraggiamento. Ripetiamo il procedimento considerandolo.
Al posto di h
prenderò htot=h+hr,dove hr
è il coefficiente di irraggiamento:
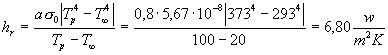
dove a=0,8 è il
coefficiente di assorbimento del materiale, in genere plastica nera, e s0=5,67·10-8 w/m2K4
è la costante di Stefan-Boltzmann.
Per cui ![]()
Il che ci porta a
calcolare ![]() sempre troppa alta!
sempre troppa alta!
CASO B - Con alettatura applicata:
Si rende necessario
quindi applicare un’alettatura come quella che si può vedere nella figura
successiva:
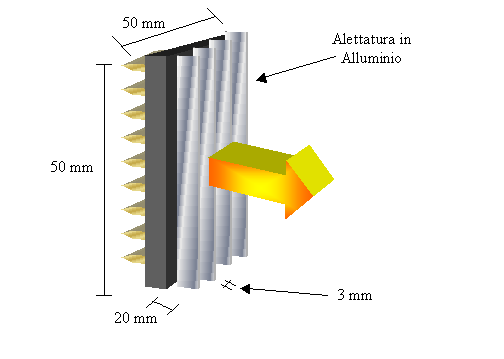
Fig. 10 – Alettatura applicata alla CPU.
Consideriamo
un’alettatura in alluminio (lall = 120w/mK) ricavata per fusione (Rc = 0). Ogni aletta ha
lunghezza L = 20 mm, larghezza pari al dispositivo, spessore s =
3 mm e dista dalla successiva 3 mm. Da ciò si deduce che il numero massimo di
alette applicabili sarà 8. Il concetto è quello di alettare la superficie per
il 50%.
Rifacendoci alla teoria abbiamo:
![]()
ma anche:
![]()
dove:
![]()
![]()
Inoltre:
![]()
da cui notiamo che lo sviluppo completo delle alette è decisamente maggiore dell’area della CPU.
Calcoliamo inoltre il fattore che ci consentirà di trovare il valore di efficienza dell’aletta, prendendo come valore di h quello che non tiene conto della parte radiante, cioè 9,56:
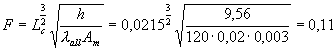
conoscendo il quale possiamo ricavare l’efficienza sul diagramma di Fig.9 che risulta eA=0,97.
Inoltre, conoscendo:
![]()
ricaviamo la temperatura:
![]()
che è un valore inaccettabile.
Supponiamo quindi di raddoppiare la lunghezza delle alette, da 20 a 40mm, ciò causerà un calo del rendimento, ma mi abbasserà sicuramente la temperatura a valori accettabili.
Si ottiene quindi:
![]()
Da cui si ricava sempre da figura 9 che eA = 0.93, quindi rifacendo i calcoli precedenti si ottiene un valore di temperatura di 85 gradi.
Potevo inoltre migliorare le prestazioni aumentando il coefficiente di convezione applicando una ventola (in convezione forzata il coefficiente di convezione risulterebbe 30 – 35 volte superiore). Così facendo avremmo aumentato la dissipazione e diminuito la temperatura; oppure colorando le alette di nero, ciò ci avrebbe fatto recuperare qualche W/m².
Sulle moderne CPU si trova oltre che all’ accoppiata dissipatore ventola un tappetino siliconico termoconduttivo (in rosa nella figura 12), si tratta di una pasta di silicone dalle elevate proprietà termoconduttive che è in grado di riempire eventuali irregolarità delle superfici metalliche a contatto che potrebbero limitare la trasmissione del calore.

Fig. 12 – Particolare del tappetino termoconduttivo.
Le schede madri stesse possiedono sensori per il monitoraggio della temperatura dei processori e delle altre componenti che grazie a software appositi (un esempio alla figura 13), mentre lavoriamo col nostro computer monitorizzano la situazione.
Questo ci fornisce una misura della importanza fornita dai produttori di componenti elettroniche allo smaltimento del calore. Perché non si ripetano più spiacevoli situazioni, come quella del PENTIUM PRO per cui tutti i primi processori entrati sul mercato bruciavano inesorabilmente.