Analisi
Armonica del Suono
La maggior parte, anzi la quasi totalità dei suoni che udiamo nel mondo reale, non sono suoni semplici, o puri, ma suoni complessi, cioè suoni composti da una maggiore o minore quantità di suoni puri; questi vengono detti componenti del suono complesso.Per meglio comprendere questo fenomeno, stabiliamo un’analogia con l’ottica.È noto come alcuni colori, detti fondamentali, siano puri, cioè non ulteriormente scomponibili. Questi colori sono il rosso, il giallo e il blu. A ciascuno di essi corrisponde una certa lunghezza d’onda del raggio luminoso, e il prisma (che scompone la luce bianca nei sette colori dello spettro luminoso) mostrerà solamente quella componente. La medesima cosa avviene per il suono. A una certa lunghezza d’onda del suono corrisponde una certa altezza percepita. Se non è presente contemporaneamente nessun’altra frequenza, il suono sarà puro.Un suono puro, o sinusoide, ha forma d’onda sinusoidale, ed è la rappresentazione della funzione trigonometrica
sin (x)
ed è costituito da una sola frequenza, senza armoniche. Viene detto perciò anche suono puro. Se le componenti sono in rapporto di frequenza intero con la componente di frequenza più bassa, si dicono armoniche. La componente a frequenza più bassa si chiama fondamentale o prima armonica; la componente di frequenza doppia della fondamentale si chiama seconda armonica;la componente di frequenza tripla della fondamentale si chiama terza armonica, etc. Per la definizione dello spettro di un suono armonico, se supponiamo che siano sempre presenti tutte le armoniche (fino al limite superiore di udibilità, dal momento che componenti ultrasoniche non influenzano la percezione timbrica), sarà sufficiente definire le ampiezze di tutte queste armoniche, per esempio con tabelle di questo genere:
|
ARMONICA |
I |
II |
III |
IV |
V |
VI |
VII etc. |
|
AMPIEZZA |
1 |
0.5 |
0.33 |
0.25 |
0.2 |
0.13 |
0.2 etc. |
che può anche essere rappresentata in grafico:

Questo è lo spettro di un suono: sull’asse orizzontale vi sono le frequenze, in kHz, sull’asse verticale le ampiezze in dB. Si può notare come questo spettro sia di tipo armonico, in quanto le frequenze sono equispaziate: ciò significa che sono tutte in rapporto armonico con la fondamentale, infatti sono presenti le frequenze: .1, .2, .3, .4, .5, .6, .7, .8, .9, 1 kHz, che equivalgono a: 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000 Hz. Sono quindi presenti tutte le armoniche fino alla X. In figura è mostrato uno spettro di tipo armonico (figura sopra). Si può notare come questo tipo di spettro dia luogo a un’onda periodica (figura sotto); è infatti ben visibile la ripetizione della forma d’onda nella parte destra della figura in basso.

Le componenti possono però essere in rapporti non armonici, come si può vedere in figura:
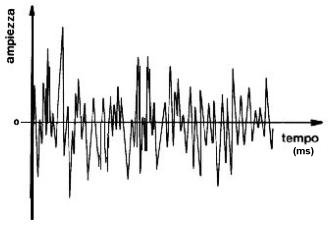

Le frequenze non sono più equispaziate, e i rapporti di frequenza con la più bassa non sono interi, anzi sono addirittura irrazionali. L’onda risultante non è quindi periodica, e infatti nella rappresentazione dell’onda non si notano ripetizioni, non è possibile individuare i cicli. I suoni periodici (o meglio, quasi periodici, dal momento che in fisica si definisce periodico un fenomeno che prosegue all’infinito) vengono percepiti come dotati di altezza definita, per esempio i suoni degli strumenti musicali ad altezza determinata o i suoni vocalici nella voce umana. I suoni non periodici invece non vengono percepiti come dotati di altezza definita; al massimo è possibile individuare una gamma o banda di frequenza in cui c’è un addensamento di componenti dotate di ampiezza rilevante; per esempio i suoni degli strumenti musicali ad altezza non definita (piatti, gong, triangolo) o i suoni consonantici della voce umana. Abbiamo fino a qui costruito suoni complessi con la somma di suoni semplici, si è cioè svolto un processo di sintesi. Ma è anche possibile effettuare il cammino opposto, di analisi, cioè scomporre un suono complesso nelle sue componenti.
Il teorema di Fourier (dal filosofo e scienziato francese Jean Baptiste Fourier) assicura che qualsiasi forma d’onda, purché periodica, è rappresentabile con una serie di armoniche, ciascuna dotata di una particolare ampiezza (e fase); è quindi possibile ricavare lo spettro di qualsiasi suono periodico. Da quanto si è detto è evidente la differenza del parametro timbro rispetto agli altri due precedentemente esaminati (frequenza e ampiezza): mentre infatti queste ultime sono grandezze unidimensionali (un solo numero è cioè sufficiente alla loro completa definizione, ed esse possono essere rappresentate da punti su una retta, così che è sempre possibile affermare per esempio che una certa frequenza è maggiore di un’altra), il timbro (o meglio, lo spettro) è una grandezza pluridimensionale (per la sua definizione è necessaria una serie di numeri, le ampiezze di ciascuna componente).
Ne deriva che non è possibile organizzare gli spettri in scale, come per la frequenza e l’ampiezza, poiché un determinato spettro non è rappresentabile come punto di una retta, bensì come punto di una spazio a n dimensioni, o n- dimensionale, dove n è il numero di componenti di ampiezza diversa da zero. Ricordiamo quanto detto nel cap. 6 a proposito della somma di onde: istante per istante i valori istantanei dell’ampiezza delle diverse onde si sommano algebricamente, cioè con il loro segno, positivo o negativo. Quando due onde della stessa frequenza si sommano, si ha il fenomeno dell’ interferenza. Quindi se due onde hanno la stessa frequenza, l’ampiezza risultante dalla loro somma sarà la somma delle singole ampiezze. Questo è però vero se le due onde sono in fase, cioè se i loro picchi positivi coincidono. Se le due onde non sono in fase, picchi positivi e picchi negativi non coincidono più, e quindi l’ampiezza massima andrà calcolata sommando punto per punto le ampiezze istantanee delle due onde. Se poi le due onde sono sfasate di un semiperiodo ( o sono, come si dice, in controfase), allora l’ampiezza dell’onda risultante risulterà dalla differenza delle ampiezze massime delle due onde. Al limite, se le due onde sono in controfase e le loro ampiezze sono uguali, la loro somma sarà nulla, in quanto le due onde si annulleranno reciprocamente.

Consideriamo invece la somma di due onde di frequenza poco diversa, come nella figura seguente:

Inizialmente le due onde siano in fase. Dopo un certo numero di periodi, a causa della lieve differenza di frequenza, si troveranno in controfase, e le ampiezze si sottrarranno. Dopo un certo altro numero di periodi le onde saranno di nuovo in fase, e così via. Il risultato sarà una oscillazione dell’ampiezza dell’onda risultante, e questa oscillazione avrà frequenza pari alla differenza di frequenza delle due onde che lo provocano. Questo fenomeno si chiama battimento. Se la differenza di frequenza è superiore alla minima frequenza udibile (circa 30 Hz), in certe condizioni la frequenza di battimento diviene udibile, e dà luogo al cosiddetto suono differenziale o terzo suono di Tartini.
Microfoni
Scopo del microfono è di convertire, o trasdurre, l’energia acustica
(meccanica) in energia elettrica.
Esistono diversi tipi di microfoni, che si basano su principi fisici diversi;
nell’audio professionale si usano solo microfoni a bassa impedenza (600
Ω) e con collegamento bilanciato, per minimizzare i disturbi captati dai
cavi. Praticamente si usano solo microfoni dinamici e microfoni a
condensatore. Questi ultimi sono di altissima qualità, ma sono delicati e
necessitano di alimentazione esterna a 48 V (phantom power, così
chiamata perché viene fornita ai microfoni con gli stessi conduttori del
segnale), in genere fornita dal mixer. Per i microfoni si usano quasi
universalmente connettori tipo XLR (detti anche Cannon), in cui, sul cavo, il
connettore femmina è dal lato microfono e quello maschio dal lato mixer.
Nella tabella seguente si riassumono le caratteristiche dei principali tipi di microfono:
|
Tipo |
Tensione di uscita |
Impedenza |
Qualità |
Note |
|
Dinamico |
Da 1 a 10 mV |
Alta o bassa |
Da cattiva a molto buona |
Robusti |
|
A condensatore |
1 mV |
Bassa |
Ottima |
Delicati, necessitano |
|
A elettrete |
1 mV |
Bassa |
Discreta |
Necessitano di batterie |
|
Piezoelettrico |
100 mV |
Alta |
Cattiva |
|
1. CHE COSA È IL
MICROFONO
Il microfono è un trasduttore di segnale: trasforma infatti l’energia meccanica del suono in energia elettrica. Senza il microfono non sarebbe possibile la registrazione di suoni, Il microfono è perciò un elemento essenziale della catena elettroacustica (microfono / amplificatore / registratore / altoparlante). Attualmente è anche l’elemento più delicato e più debole della catena. Poiché contiene parti meccaniche, che per ottenere una buona qualità devono essere di altissima precisione, è anche l’elemento più costoso (almeno per quanto riguarda i modelli di alta qualità).
2. LE CARATTERISTICHE DEI
MICROFONI
Le caratteristiche fondamentali di un microfono sono:
a. Il principio di trasduzione: a condensatore, dinamico, a electret, piezoelettrici
b. la risposta in frequenza, che dovrebbe essere il più possibile regolare (piatta). A prescindere da usi particolari, i microfoni usati nella musica dovrebbero essere quanto piú lineari possibile, e comunque non avere variazioni di livello di uscita superiori a 3 dB nella banda di frequenza comprese fra 30 e 20000 Hz.
c. La sensibilità è il rapporto fra ampiezza del segnale elettrico uscente dal microfono e ampiezza del segnale acustico, è cioè un’espressione del rendimento del microfono. Viene di solito espressa in mV/µbar (milliVolt per microbar). 1 µbar corrisponde a 74 dB. Valori usuali sono di 1 mV/µbar, dal che si può dedurre che il segnale uscente da un microfono è molto basso, circa 300 volte minore del segnale uscente dalle altre apparecchiature dello studio; esso va perciò preamplificato per portarlo allo stesso livello degli altri segnali. Gli ingressi per microfono presenti nelle apparecchiature sono perciò diversi dagli ingressi per segnali ad alto livello detti ingressi di linea.
d. La massima pressione acustica o pressione acustica limite, espressa in dB, specialmente critica per la registrazione di strumenti in grado di produrre suoni di grande intensità, come gli strumenti a percussione.
e. La direzionalità esprime la capacità del microfono di captare piú o meno bene i segnali in base alla direzione di provenienza. In figura sono indicate le caratteristiche direzionali di microfoni omnidirezionali (o panoramici), unidirezionali (a cardioide), bidirezionali (a otto) e superdirezionali (a clava). La direzione frontale è indicata con l’angolo di 0°, quella posteriore con l’angolo di 180°. Osservando il diagramma di un microfono omnidirezionale, si nota che la sensibilità è la medesima per i suoni che provengono da qualsiasi direzione. Per un microfono a cardioide (cosí chiamato perché la sua caratteristica direzionale ha approssimativamente la forma di un cuore), si nota che per i suoni provenienti dalla direzione frontale (0°) la sensibilità è quella nominale di 0 dB; ma, via via che la sorgente sonora si sposta, al sensibilità diminuisce, per ridursi di 24 dB quando la direzione di provenienza è posta dietro il microfono (180°).
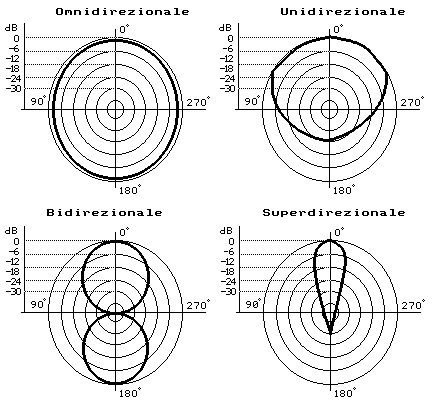
Grande importanza ha poi, nei microfoni direzionali, la variazione della caratteristica in funzione della frequenza: la direzionalità è infatti piú accentuata per le frequenza alte, mentre alle frequenze basse il microfono si comporta praticamente come panoramico. Questo fenomeno, insito nel principio di trasduzione dei microfono, può dare luogo, se trascurato, a difetti nella ripresa del suono, ma può anche suggerire particolari tecniche di ripresa microfonica. Alcuni microfoni dispongono di un selettore che permette di variarne la caratteristica direzionale, e quasi tutti quelli di elevata qualità comprendono un filtro passa-alto, detto di roll-off, che consente una attenuazione delle basse frequenze (di solito da 80 Hz in giù), indispensabile in ambienti particolarmente riflettenti per evitare il cosiddetto "effetto rimbombo".
Sotto l’aspetto del principio di funzionamento, gli unici microfoni che consentono una ottima qualità per usi musicali sono quelli dinamici (di solito a bobina mobile) e quelli a condensatore. La qualità migliore in assoluto si ottiene con i microfoni a condensatore, che sono però piuttosto delicati (sensibili agli agenti atmosferici e agli urti) e necessitano di una alimentazione in corrente continua di 48 Volt (phantom power), che può essere fornita dal mixer, o, in mancanza, da appositi alimentatori. I microfoni a elettrete si basano sullo stesso principio di quelli a consensatore (pur essendo di qualità nettamente inferiore), ma date le diverse caratteristiche costruttive possono essere alimentati a batterie, di piccole dimensioni e di lunga durata, che sono alloggiate nel corpo stesso del microfono. I microfoni dinamici forniscono una buona qualità, sebbene inferiore a quelli a condensatore, non necessitano di alcuna alimentazione, sono robusti e in grado di sopportare notevoli sovraccarichi acustici.
3. MICROFONI DINAMICI
Il principio di funzionamento dei microfoni dinamici si basa sull’effetto
elettromagnetico: quando in un campo magnetico viene fatto muovere un
conduttore, in questo conduttore si genera una corrente elettrica I .
Quanto più intenso sarà il campo magnetico, tanto più intensa sarà la corrente
elettrica che si genera. Quando in un conduttore circola corrente elettrica,
per la legge di Ohm ai suoi capi si crea una differenza di potenzale,
cioè una tensione elettrica, che rappresenta le variazioni di pressione
dell’onda sonora, ed è proprio il segnale che desideriamo esca dal microfono.
Elemento essenziale del microfono è il diaframma, cioè un piccolo
elemento, di solito a forma circolare e al giorno d’oggi di materiale plastico
speciale, che viene messo in vibrazione dalle onde sonore.

Al diaframma è collegata una bobina mobile (il conduttore indicato in figura) immersa in una campo magnetico generato da un piccolo magnete fisso, di solito a forma di anello. Quando il diaframma, messo in vibrazione dalle onde sonore, si muove oscillando in su e in giù, fa muovere anche la bobina ad esso solidale, e ai capi della bobina si genera una tensione elettrica che segue, più o meno fedelmente, l’andamento dell’onda sonora.
Vi sono diversi tipi di microfoni dinamici, che si differenziano moltissimo a seconda della qualità (da pochi Euro, come i microfoni forniti di serie con le schede audio più comuni, e adatti per applicazioni vocali) fino a centinaia di Euro, adatti per applicazioni musicali. Fra le caratteristiche dei microfoni dinamici si può ancora citare la relativa insensibilità ai rumori meccanici esterni (come il maneggiamento del microfono) e lo spiccato effetto di prossimità, cioè la caratteristica di variare la risposta in frequenza, e quindi la timbrica, a seconda della distanza del microfono dalla sorgente sonora. I microfoni dinamici sopportano, generalmente, elevate pressioni acustiche. Fra i modelli più noti i Sennheiser MD421 e MD422, gli Shure SM57, SM58, Beta 52 e Beta 58, gli Electrovoice PL20, e gli AKG D12 e 112.
4. MICROFONI A CONDENSATORE
Un condensatore è un apparato elettrico costituito da due piastre di materiale conduttore, separate da un isolante (aria o altro, chiamato dielettrico). Se alle due piastre viene applicata una tensione continua, non vi è passaggio di corrente, mentre se alle piastre viene applicata una tensione alternata la corrente passa, più o meno bene a seconda della sua frequenza e della distanza fra le piastre. Nel microfono a condensatore una delle piastre è fissa, mentre l’altra è costituita dal diaframma messo in vibrazione dalle onde sonore, ed è perciò mobile: la distanza fra le piastre varia quindi a seconda della posizione del diaframma.

Alle piastre viene applicata una tensione continua di 48 Volt, chiamata phantom power (alimentazione fantasma) che viaggia sugli stessi conduttori usati per portare il segnale. Quando il diaframma è sollecitato da un’onda sonora si muove, e la distanza fra le piastre varia, modulando perciò la tensione continua. Con adatti circuiti la tensione continua viene eliminata, e rimante soltanto la parte alternata, che costituisce proprio il segnale elettrico che ci serve, e che segue l’andamento di pressione dell’onda sonora. Fra le caratteristiche dei microfoni a condensatore è l’elevata sensibilità, e la delicatazza, oltre che la sensibilità ai rumori meccanici, come il maneggiamento del microfono. Fra i modelli più noti i quasi mitici Neumann U84 (il microfono di riferimento, specialmente per la voce) e TLM103, gli Schoeps CMC5, gli AKG 414, gli Shure SM81 e Beta 87, e i Sennheiser MKH 40P48.
Costanti di Tempo
Il rivelatore è uno strumento che trasforma il segnale elettrico alternato, filtrato o meno, in una tensione continua proporzionale al valore efficace o al valore di picco del fenomeno rilevato, che va poi a pilotare l’indice del quadrante di misura. Inoltre esso provvede alle costanti di tempo e cioè a determinare la rapidità con la quale l’indice dello strumento segue le variazioni del segnale. La velocità di risposta dell’indice dello strumento viene determinata dal tempo di integrazione scelto (più lungo è il tempo di integrazione, più piccole saranno le fluttuazioni) per cui il livello massimo che viene raggiunto dall’indice è funzione di tale costante di tempo oltreché del tipo di rumore in esame. Anche le varie costanti di tempo sono state normalizzate internazionalmente e, precisamente:
- slow (lenta): tempo di integrazione 1050 msec; decade di 10dB in meno di 3 sec dal momento in cui cessa il segnale;
- fast (veloce): tempo di integrazione 125 msec; decade di 10 dB in meno di 0,5 sec dal momento in cui cessa il segnale;
- impulse (impulsiva): tempo di integrazione 35 msec; decade di circa 3 dB al sec; dispone anche del circuito di memoria (hold);
- peak (picco): tempo di inerzia 0,02 msec; data l’estrema velocità di risposta l’uscita da tale circuito viene necessariamente inviata al circuito di memoria (hold).
E’ importante sottolineare che le costanti slow, fast e impulse esprimono un dato RMS, mentre la peak è indice del valore di picco.
Dalla differenza dB peak h - dB imp h, cioè dalla differenza tra il valore di picco e il valore RMS, si può avere in prima approssimazione un’idea della forma d’onda dell’impulso sonoro: più l’onda è stretta maggiore sarà tale differenza.
Altra annotazione importante è che, dato un impulso sonoro, l’area sottesa dalle risposte fast e slow è identica ed inferiore a quella che si ricava con impulse.
Quanto detto prima si può anche intendere nei termini seguenti: se si analizza statisticamente una serie di impulsi sonori successivi con le tre diverse costanti di tempo RMS, usando tempi di campionamento sufficientemente brevi si otterrà un valore identico per slow e fast ed un valore maggiorato per impulse.
Nella quasi totalità le normative esistenti fanno riferimento a valori valutati in RMS e tuttavia il valore di picco può essere molto importante soprattutto in due casi:
- per valutare il carico acustico fisico sulla membrana timpanica dovuto ad un impulso;
- per garantirci che il fattore di cresta del segnale che si intende misurare sia compatibile con le caratteristiche dello strumento usato (fattore di cresta = valore di picco / valore efficace).
APPENDICE:
Il valore di picco esprime la massima escursione della pressione rispetto alla pressione statica del mezzo presa in modulo; il valore di picco-picco, è dato invece dall'escursione massima positiva più l'escursione massima negativa sempre valutata come modulo. Il valore medio, poco usato in acustica, è dato dalla somma delle diverse variazioni della pressione in funzione del tempo, divisa per il tempo durante il quale la somma viene eseguita:
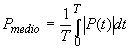
Il valore efficace (RMS) è quello che rappresenta meglio il contenuto energetico dell'onda, si rappresenta matematicamente come:

Le onde sonore emesse dalla sorgente si propagano nello spazio attraverso superfici sempre più grandi; il rapporto W/S definisce l'intensità acustica I del suono sulla superficie S. Il suono in un certo punto dello spazio viene valutato attraverso la misurazione della pressione sonora p la quale dipende, oltre che dalla potenza W della sorgente e dalla distanza di questa dal punto considerato, anche da diverse condizioni ambientali e di propagazione. In sintesi si può affermare che la potenza sonora è la causa dell'inquinamento acustico, mentre la pressione sonora ne è l'effetto ed è la grandezza che viene misurata in pratica.
Impedenza e intensità acustica
L'impedenza acustica è una grandezza complessa (cioé dotata di parte reale e parte immaginaria), data dal rapporto tra la pressione acustica [Pa] e la velocità [m/s] delle particelle di fluido indotta dal passaggio dell'onda, entrambe in rappresentazione complessa. L'impedenza acustica sintetizza le caratteristiche di un sistema acustico proprio come l'impedenza elettrica sintetizza le caratteristiche di un circuito elettrico. Infatti, la parte reale dell'impedenza acustica dipende dall'attitudine del sistema a dissipare energia acustica, mentre la parte immaginaria indica la capacità del sistema di immagazzinare energia acustica e di restituirla sfasata.
![]()
![]()
c = velocità del suono
![]() = densità dell’aria
= densità dell’aria
L’impedenza viene espressa come rapporto tra i moduli e questa è infatti una caratteristica delle onde piane: "la pressione sonora e la velocità sono in fase."
In questo caso prende il nome di impedenza acustica caratteristica.
Per onde sonore generiche diventa impedenza acustica specifica ed è un numero complesso, in conseguenza del fatto che pressione e velocità non sono in fase tra loro.
Esprimendo tutto con le formule di Eulero.
![]()
![]()
Si ottiene l’impedenza in forma complessa: ![]()
Esempio: Calcolare l’impedenza caratteristica dell’aria alla temperatura
di 20 °C.
v = 340 m/s
p = 1,2 kg/m3
Z = p / v = p0c = 1,2 * 340 = 408 Rayl
Il valore dell’intensità acustica si ricava facendo la media temporale dell’intensità istantanea:
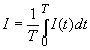
misurata in W/m2.
Ma ricordandosi l’espressione dell’intensità istantanea. ![]()
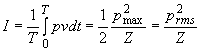
Questa formula vale solo quando pressione e intensità acustica sono in fase. Normalmente si deve considerare che l’impedenza Z è complessa e introduce quindi uno sfasamento.
I Livelli Sonori
Abbiamo visto, nel paragrafo precedente, che i valori della pressione sonora p e
dell’intensità acustica I variano su range piuttosto ampi: in particolare,
abbiamo visto che la pressione sonora (cioè la variazione di pressione
rispetto al valore atmosferico) varia nell’intervallo ![]() .
.
Il valore minimo di 20 µPa è un valore medio statistico ritenuto appunto come il
minimo percepibile dall’ascoltatore medio; il valore di 104 Pa, invece, corrisponde pressoché a quello che si percepisce per un colpo di arma da fuoco, a distanza ravvicinata.
|
Livello di intensità dB |
Condizione ambientale |
Effetto sull'uomo |
|
120 |
Soglia del dolore |
Lesioni dell’orecchio |
|
110 |
Picchi d’intensità di una grande orchestra |
Zona pericolosa per l'orecchio |
|
100 |
Interno della metropolitana |
|
|
90 |
Picchi di intensità di un pianoforte |
|
|
80 |
Via a circolazione media |
Zona di fatica |
|
75 |
Voce forte, a un metro |
|
|
70 |
Conversazione normale, a un metro |
|
|
60 |
Ufficio commerciale |
|
|
50 |
Salotto calmo |
Zona di riposo (giorno) |
|
40 |
Biblioteca |
|
|
30 |
Camera da letto molto calma ( notte) |
Zona di riposo (notte) |
|
20 |
Studio di radiodiffusione |
|
|
0 |
Soglia di udibilità |
E’ quindi conveniente esprimere queste grandezze in scala logaritmica.
Per fare questo, si introducono i cosiddetti livelli di grandezze acustiche contemporaneamente si introduce il Decibel (simbolo dB), sottomultiplo del Bel, ma oggi comunemente usato per le misure di acustica.
Livello di pressione sonora:
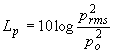
con p0 = 2 µPa valore di riferimento.
Esistono diversi Livelli ognuno riferito ad una diversa grandezza acustica.
Livello di intensità acustica:
![]()
con I0 = 10-12 W/m2.
Essendo il logaritmo una funzione invertibile, se conosciamo il livello di intensità acustica, possiamo facilmente ricavare l’intensità acustica espressa in unità naturali:
![]()
Livello di densità sonora:
![]()
il cui valore di riferimento è D0 = 3 · 1015 J/m3
Livello di potenza acustica:
![]()
con W0 = 10 –12 W.
Analogamente a quanto fatto prima possiamo ricavare la densità sonora W.
![]()
Livello di velocità :

E’ importante notare che i vari valori di riferimento sono stati scelti in modo tale che i relativi livelli risultassero tra loro correlati in maniera opportuna.
In molte situazioni di misura le fluttuazioni del livello sonoro sono troppo ampie e irregolari per consentire una lettura precisa, persino usando la costante di misura slow. Si possono facilitare e rendere più precise le misure di rumore impulsivo o ampiamente fluttuante utilizzando il concetto di livello equivalente (Leq), definito come la vera energia media del livello sonoro nell'intero periodo di misura. Matematicamente esso si desume dalla equazione:
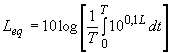
rappresentando pertanto la media ponderata in termini energetici dell'area sottesa dall'andamento di l.p.s. in funzione del tempo. La misura del Leq su tempi brevi facilita il confronto di singoli eventi quali il transito di veicoli, il passaggio di treni, ecc. , mentre la misura del Leq su tempi lunghi consente la valutazione precisa del rumore delle comunità, consentendo il raffronto alle più recenti normative tecniche.
SOMMA DI SEGNALI
La somma di due o più livelli sonori può essere coerente o incoerente.
Se i due segnali sono coerenti significa che le due onde corrispondenti ai due segnali sono perfettamente identiche e in fase. Inoltre si deve avere che la distanza dell’ascoltatore o del microfono sia la stessa da entrambe le sorgenti.
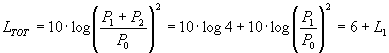
in quanto P1 = P2.
Nel caso si sommino due segnali con L = 80 dB
![]() dB
dB
Solitamente però la somma di due segnali è da intendersi come somma incoerente.
Questo può essere il caso di due casse acustiche collegate ad uno stereo: i due segnali sono diversi perché hanno fase casuale a causa delle riflessioni nell’ambiente. Ci possono allora essere momenti in cui due picchi di pressione si sommano enfatizzandosi e altri in cui un picco ed una valle si sommano eliminandosi. In tal caso per il principio di conservazione dell’energia l’intensità sonora è data dalla somma delle due intensità dei segnali reali, la densità di energia sonora à data dalla somma delle due densità mentre per la pressione non vale tale uguaglianza. La pressione al quadrato risulta proporzionale alla densità di energia e vale la formula:
![]()
Per cui la formula della somma risulta essere:

o l’equivalente:
![]()
Esempio:
Supponiamo di avere due suoni cui corrispondono i livelli di intensità L1 = 70 dB e L2 = 70 dB. Calcoliamo il livello di intensità totale.
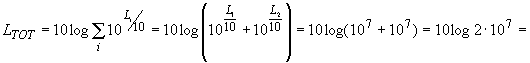
![]()
In generale il calcolo del livello si può eseguire attraverso un grafico.

Data la differenza tra idue livelli si ottiene il valore da aggiungere al maggiore dei due. Infatti grazie alle proprietà del logaritmo il valore da sommare dipende solo dalla differenza di livello tra i due segnali e non dal livello di partenza.
Se per esempio i due livelli sonori fossero di 70 dB e di 65 dB la loro somma incoerente sarebbe:
![]() .
.