 (1)
(1)Esercizi sullo scambio termico per convezione
Richiami di Teoria:
Gran parte dei fenomeni legati allo scambio termico per convezione possono essere studiati calcolando il coefficiente di convezione h dato dalla relazione:
 (1)
(1)
Quindi è necessario conoscere il numero di Nusselt Nu=f(Re,Gr,Pr,x/L) che nel caso più generale può essere ricavato tramite una formula del tipo:
![]() (2)
(2)
L' espressione può essere semplificata di alcuni termini in alcuni casi particolari:
d'inerzia, quindi scompare il numero di Reynolds Re.
![]() (3)
(3)
Analiticamente si ottiene:
 (4)
(4)
![]()
![]() Si osserva quindi che perché L scompaia dall' equazione si deve avere b=0.33, infatti solo questo valore verifica la relazione (L3 )b=L.
Si osserva quindi che perché L scompaia dall' equazione si deve avere b=0.33, infatti solo questo valore verifica la relazione (L3 )b=L.
Se il moto del fluido è altresì laminare si pone b=c, ottenendo così un nuovo numero detto numero di Rayleigh: Ra=Gr∙Pr.
Il numero di Nussel si esprime allora nella forma Nu=C. Ra.
Un caso simile si verifica nel caso di convezione forzata e moto laminare in cui si pone a=c e si definisce il numero di Plecect: Pe=Re. Pr.
Il numero di Nussel si esprime allora nella forma Nu=C. Pe.
Per farsi un’idea sul caso di convezione che si viene a dover trattare, in prima approssimazione si può considerare:
In pratica, una volta calcolati i numeri di Pr e Gr si calcola il numero di Re, dopodichè si consultano le tabelle presenti nell’appendice che ci forniscono i parametri a, b, c delle relative equazioni in base al valore di Re ed alla geometria del sistema.
Esercizio N° 1
Si consideri un tubo circolare di diametro D=50mm in cui scorre acqua riscaldata alla velocità media w=2m/s. Trovare il coefficiente di convezione interno h.
Inoltre sapendo che la potenza termica scambiata Q=2017W ,conoscendo la lunghezza del tubo L=10m e la temperatura interna T=80° C calcolare la temperatura esterna della parete del tubo.
Risoluzione:
![]() Calcoliamo subito il numero di Reynolds per determinare il tipo di moto del fluido all’interno del tubo:
Calcoliamo subito il numero di Reynolds per determinare il tipo di moto del fluido all’interno del tubo:
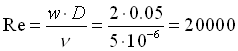
![]() Il numero di Reynolds è maggiore di 10000 quindi siamo in presenza di moto turbolento, perciò utilizziamo la formula di Dittus e Boelter per fluidi riscaldati (vedi tabella 2 nell’appendice):
Il numero di Reynolds è maggiore di 10000 quindi siamo in presenza di moto turbolento, perciò utilizziamo la formula di Dittus e Boelter per fluidi riscaldati (vedi tabella 2 nell’appendice):
![]() (6)
(6)
Per calcolare il numero di Nusselt dobbiamo calcolare il numero di Prandtl:
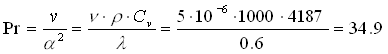 (7)
(7)
Il numero di Nusselt risulta quindi:
![]() (8)
(8)
Dalla relazione che lega il numero di Nusselt e il coefficiente di convezione interna:
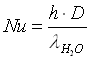 (9)
(9)
otteniamo il valore del coefficiente di convezione interno:
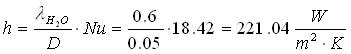 (10)
(10)
Conoscendo il valore della potenza termica scambiata Q=2017W e calcolando il valore della portata in massa otteniamo la temperatura esterna del tubo:
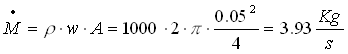 (11)
(11)
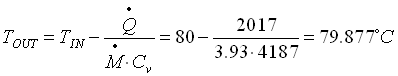 (12)
(12)
Esercizio N° 2
Avendo un tubo di lamiera a sezione quadrata attraverso il quale si scaricano fumi caldi (tiraggio di un camino) calcolare la temperatura esterna del tubo.
Dati del problema:
Risoluzione:
Risolvendo questo problema utilizzeremo due equazioni che ci definiscono la potenza termica scambiata; infatti da una prima equazione sullo scambio termico otteniamo:
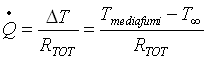 (13)
(13)
e da un bilancio dell’entalpia otteniamo invece:
![]() (14)
(14)
Supponiamo ora che il tubo sia circolare perché ai fini pratici l’errore commesso è accettabile.
Definiamo ora la resistenza termica equivalente ![]() che è data dalla somma di tre contributi dovuti a tre resistenze diverse:
che è data dalla somma di tre contributi dovuti a tre resistenze diverse:
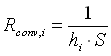 (15)
(15)
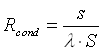 (16)
(16)
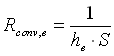 (17)
(17)
Determiniamo ora il coefficiente di convezione interno:
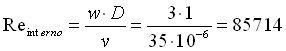 (18)
(18)
Il numero di Reynolds è maggiore di 10000, siamo allora in presenza all’interno del tubo di un regime turbolento, il numero di Prandtl in questo caso vale Pr = 0.71, quindi possiamo calcolare il numero di Nusselt con la formula di Dittus e Boelter (vedere tabella 2 dell’appendice):
![]() (19)
(19)
possiamo allora calcolare il coeff. di convezione interno:
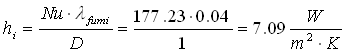 (20)
(20)
Determiniamo ora il coeff. di convezione esterno:
supponiamo allora che all’esterno del tubo ci troviamo in presenza di convezione naturale, calcoliamo quindi il numero di Grashof Gr:
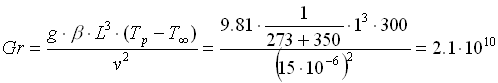 (21)
(21)
dove come valore di Tp è stato preso un valore "casuale" che verrà successivamente migliorato con successive approssimazioni; infatti, una volta trovata la temperatura esterna della parete, la sostituiremo a Tp nella formula (14) fino ad ottenere un risultato con variazioni minime. La grandezza L rappresenta invece id diametro del tubo.
Il numero di Rayleigh vale quindi:
![]() (22)
(22)
per cui il moto esterno è turbolento (aria che si muove per convezione naturale), quindi il numero di Nusselt vale (vedi tabella 3 dell’appendice):
![]() (23)
(23)
possiamo allora calcolare il coeff. di convezione esterno he:
 (24)
(24)
Ora abbiamo tutti gli elementi per calcolare la resistenza termica totale RTOT che vale:
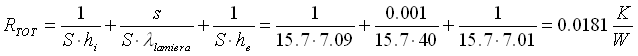 (25)
(25)
dove ![]() (26)
(26)
Quindi la potenza termica scambiata vale:
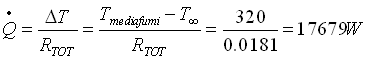 (27)
(27)
la portata in massa vale:
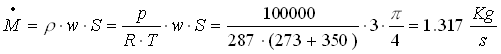 (28)
(28)
quindi posso calcolare la temperatura esterna della parete TOUT che vale:
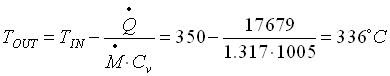 (29)
(29)
Adesso andiamo a calcolare ancora il numero di Grashof Gr sostituendo al valore di TP il valore di TOUT appena trovato nell’equazione (29):
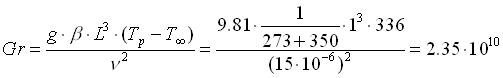 (30)
(30)
quindi andiamo a calcolare la nuova temperatura esterna della parete procedendo come prima, perciò otteniamo:
![]()
![]() (32)
(32)
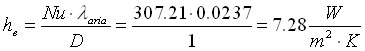 (33)
(33)
 (34)
(34)
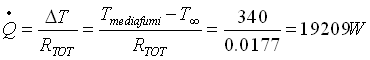 (35)
(35)
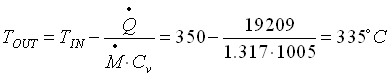 (36)
(36)
che è il nostro risultato definitivo dato che subisce una minima variazione rispetto alla precedente temperatura esterna del tubo che era stata calcolata nell’equazione (29).
Appendice:Tabelle
|
Sezione del condotto |
Condizioni al contorno |
||
|
Flusso di calore alla parete = cost |
Temperatura della parete = cost |
||
|
Circolare |
4.36 |
3.66 |
|
|
Quadrata a = b |
3.63 |
2.98 |
|
|
Rettangolare |
a = 1.4 b |
3.73 |
3.08 |
|
a = 2 b |
4.11 |
3.40 |
|
|
a = 3 b |
4.79 |
3.96 |
|
|
a = 4 b |
5.35 |
4.44 |
|
|
a = 8 b |
6.49 |
5.60 |
|
|
a = ¥ |
8.24 |
7.54 |
|
|
a = ¥ con una superficie isolata |
5.38 |
4.86 |
|
|
Triangolare a = b = c |
3.11 |
2.47 |
|
Tabella 1 – Valori del numero di Nusselt per moto laminare e profili completamente sviluppati.
|
Campo di validità (Re) |
Regime |
Costante In parete |
Nu = C.Rea.Prc |
Autori |
Note |
|||||
|
Ingr. Dinamico |
Ingr. Termico |
Sviluppato |
T
|
Q |
C |
a |
c |
|||
|
< 2300 |
* |
* |
* |
0.289(D/X)1/2 |
0.5 |
0.33 |
Elser |
L < 20 D |
||
|
< 2300 |
* |
* |
1.86(D/X)1/3 |
0.33 |
0.33 |
Sieder e Tate |
X > 20 D |
|||
|
< 2300 |
* |
* |
* |
0.664(D/X)1/2 |
0.5 |
0.33 |
Pohlhaunsen |
|||
|
3000 – 30000 |
* |
* |
0.0033 |
1 |
0.37 |
Böhm |
||||
|
2700 – 7000 |
* |
* |
* |
0.01(D/X)0.37 |
1 |
0.37 |
Giulianini e altri |
1.2 D < X X < 20 D |
||
|
> 10000 |
* |
* |
0.036(D/X)1/18 |
0.8 |
0.33 |
Nusselt |
||||
|
> 10000 |
* |
0.032(D/X)1/20 |
0.8 |
0.37 |
Kraussold |
Liquido Riscaldato |
||||
|
> 10000 |
* |
0.032(D/X)1/20 |
0.8 |
0.3 |
Kraussold |
Liquido Raffreddato |
||||
|
> 10000 |
* |
0.183(D/X)1/3 |
7/12 |
0.33 |
Elser |
Teorico |
||||
|
> 10000 |
* |
* |
0.023 |
0.8 |
0.4 |
Dittus e Boelter |
Fluido Riscaldato |
|||
|
> 10000 |
* |
* |
0.023 |
0.8 |
0.3 |
Dittus e Boelter |
Fluido raffreddato |
|||
|
> 10000 |
* |
* |
0.027 |
0.8 |
0.33 |
Sieder e Tate |
Per prodotti Petroliferi |
|||
|
12000 – 220000 |
* |
* |
0.02(Di/De)0.53 |
0.8 |
0.33 |
Monrad e Pelton |
Aria o acqua sez. anulare sup. esterna isolata |
|||
Tabella 2 – Formule sperimentali per il calcolo del numero di Nusselt: convezione forzata.
|
Situazione geometrica |
Campo di validità (Ra) |
Nu=C.Grb.Prc |
Autori |
Note |
||
|
C |
b |
c |
||||
|
Superficie cilindrica orizzontale |
< 10-5 |
0.4 |
0 |
0 |
McAdams |
Nu e Gr cacolati in funzione del diametro D |
|
103 - 109 |
0.53 |
0.25 |
0.25 |
|||
|
109 - 1012 |
0.13 |
0.33 |
0.33 |
|||
|
Superficie piana o cilindrica verticale |
103 - 109 |
0.59 |
0.25 |
0.25 |
McAdams |
Nu e Gr calcolati in funzione della estensione verticale L |
|
109 - 1012 |
0.13 |
0.33 |
0.33 |
|||
|
Superficie piana orizzontale |
105 – 2.107 |
0.54 |
0.25 |
0.25 |
Fishenden e Saunders |
Flusso di calore verso l’alto |
|
2.107 – 3.1010 |
0.14 |
0.33 |
0.33 |
|||
|
Superficie piana orizzontale quadrata di lato L |
105 – 2.107 |
0.25 |
0.25 |
0.25 |
Flusso di calore verso il basso |
|
|
Sfera |
103 - 107 |
0.49 |
0.25 |
0.25 |
Bromham e Mayhew |
|
|
Strato verticale di altezza H e spes-sore L: una parete verticale più calda dell’altra |
< 2000 Pr |
1 |
0 |
0 |
Jakob |
Nu e Gr calcolati in funzione di L. Relazioni valide per l’aria |
|
(2.104 – 2.105) Pr |
0.18(H/L)-1/9 |
0.25 |
0 |
|||
|
(2.102 – 11.106) Pr |
0.065(H/L)-1/9 |
0.33 |
0 |
|||
|
< 103 |
1 |
0 |
0 |
Emery e Chu |
Nu e Gr calcolati in funzione di L. Relazioni valide per i liquidi, con 3 < Pr < 30000 |
|
|
103 - 107 |
0.28(H/L)-1/4 |
0.25 |
0.25 |
|||
Tabella 3- Formule sperimentali per il calcolo di Nusselt: convezione naturale.
|
Situazione geometrica |
Campo di Validità |
Nu = C.Rea.Grb.Prc |
Autori |
Note |
|||
|
C |
a |
b |
c |
||||
|
Condotto verticale con sezione circolare L/D=20 |
Re > 1600 |
0.525 |
0 |
0.25 |
0.25 |
Watzinger e Johnson |
Acqua che scende Raffreddandosi |
|
1600<Re<4600 |
0.255 |
0.07 |
0.25 |
0.37 |
|||
|
Condotto verticale con sezione circolare L/D=50 |
103 < Re < 105 |
0.032. .(D/X)0.05 |
0.8 |
0 |
0.37 |
Kirschbaum |
Re deve essere Modificato con l’aggiunta di un termine correttivo |
Tabella 4- Formule sperimentali per il calcolo del numero di Nusselt: convezione mista.