Pressione e velocità: analogia col pendolo semplice
Parametri acustici di tipo energetico
L'acustica è la scienza teorica e sperimentale del suono; comprende lo studio di tutti i fenomeni relativi alla produzione, alla propagazione e alla rivelazione delle onde elastiche nei mezzi solidi, liquidi e gassosi, in particolare di quelle sonore; stabilisce le leggi di vibrazione dei corpi e spiega le sensazioni acustiche fornite sia dai suoni musicali che dai rumori.
Il fenomeno del suono è tra quelli più vicini alla nostra esperienza sensoriale diretta. Una definizione approssimativa di suono può essere quella di rapida variazione di pressione prodotta in un mezzo elastico dalla vibrazione di un corpo materiale (detta sorgente sonora), che risulti percepibile attraverso gli organi dell'udito umano. Essa è inoltre una forma di trasporto di energia meccanica che avviene senza trasporto di materia. Tale trasporto per potersi compiere necessita di un mezzo, il quale deve essere dotato di massa ed elasticità, come ad esempio l'aria.
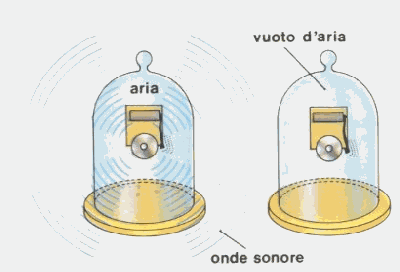
Un esperimento che si può fare per dimostrare la necessità del mezzo nella propagazione del suono è quello della campanella posta sotto una campana di vetro nella quale togliamo l'aria progressivamente tramite una pompa da vuoto. Il suono inizialmente squillante della campanella si affievolisce fino a scomparire.

Figura 1 Esperimento della campanella; una volta spinto il vuoto tramite una pompa, cioè privata l'onda acustica del mezzo, si annulla la propagazione dell'onda sonora.
Approssimando l'aria come un gas perfetto, quando un certo numero di particelle in una certa regione dello spazio subisce una perturbazione dovuta alla vibrazione di un corpo elastico si ha un moto d'assieme del fluido causato dagli urti di tali particelle che si trasmettono.
Il modello fisico che meglio spiega il comportamento del mezzo aria in queste condizioni di perturbazione è quello di una successione di volumi dotati di massa e di molle connesse tra loro. Se io perturbo la quiete di uno di questi volumi questo inizierà ad oscillare attorno alla sua posizione di equilibrio caricando e scaricando le molle che lo connettono alle masse adiacenti che, a loro volta, cominceranno ad oscillare.
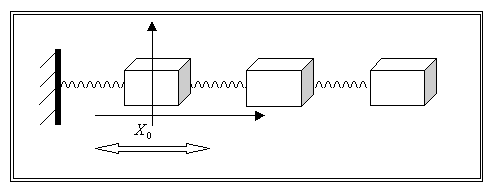
Figura 2 La figura rappresenta in modo intuitivo il mezzo elastico massivo di cui necessita l'onda sonora per propagarsi. Il comportamento dei volumi collegati tramite molle una volta sottoposti ad una perturbazione dal proprio stato di equilibrio è analogo a quello delle particelle d'aria sottoposte ad una perturbazione di tipo acustico.
Studiando più specificatamente la legge del moto di tali particelle si nota che per ognuna di esse si può definire un vettore spostamento, un vettore velocità e un vettore accelerazione. Anche se può apparire macroscopicamente che il suono abbia un moto uniforme nella direzione Sorgente - Ascoltatore, microscopicamente la legge del moto è di tipo oscillatorio. Come si può notare facilmente nel modello dei volumi collegati con molle è la perturbazione che si muove con moto uniforme, mentre le singole masse si muovono oscillando attorno alla propria posizione di equilibrio.
Per meglio comprendere il meccanismo della propagazione nel mezzo si può fare riferimento alla classica esperienza del cilindro (contenente aria) con un pistone posto ad una estremità a sua volta collegato tramite una biella ad un albero rotante.
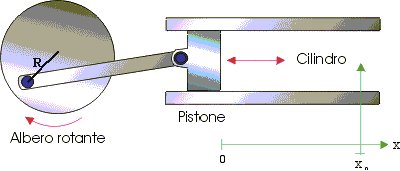
Figura 3 Cilindro con pistone collegato ad un albero motore tramite una biella. Disassamento della biella dal centro dell'albero motore è pari a R.
L'aria è un mezzo elastico cosicché, muovendo in avanti il pistone per un piccolo tratto, se ne comprime l'elemento a diretto contatto con la superficie del pistone e quindi si provoca un aumento locale di pressione. Arrestando il movimento del pistone l'elasticità dell'aria provoca allora una espansione nella direzione di allontanamento dall'origine O. (vedi fig.3)

Figura 4 Cilindro di lunghezza infinita contenente un mezzo elastico.
Le molecole che costituiscono l'elemento d'aria in pressione spingono allora quelle costituenti l'elemento adiacente comprimendolo; in questo modo per spinte successive ha luogo la propagazione, lungo il condotto. L'orecchio umano è lo strumento in grado di farci percepire le variazioni di pressione come fenomeni acustici.
Ritornando all'esperimento se l'albero motore ruota con una velocità angolare ![]() e il disassamento delle biella dal centro del cerchio è pari a R, le oscillazioni dello stantuffo e delle particelle d'aria che "appoggiano" contro lo stantuffo stesso, seguono la legge di moto armonico:
e il disassamento delle biella dal centro del cerchio è pari a R, le oscillazioni dello stantuffo e delle particelle d'aria che "appoggiano" contro lo stantuffo stesso, seguono la legge di moto armonico:
![]() (1)
(1) ![]()
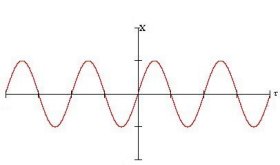
Figura 5 Andamento dell'ampiezza dell'oscillazione sinusoidale al variare del tempo. Il grafico è relativo alla formula assumendo come costanti R=1m, T=2s.
Con semplici operazioni di derivazione rispetto alla variabile tempo, possiamo ricavare l'andamento della velocità e dell'accelerazione.
![]() (2)
(2)
![]() (3)
(3)

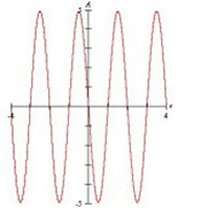
Figura 6 Andamento della velocità e della accelerazione in funzione del tempo. Nel grafico della velocità le costanti assunte sono R=1m, T=2s. Nel grafico dell'accelerazione le costanti assunte sono invece R=0.5m, T=2s.
Non è vero, però che tali leggi del moto valgano ovunque per tutte le particelle d'aria contenute nel cilindro. A causa di fenomeni di attrito e altri fenomeni dissipativi l'ampiezza e la fase di tali oscillazioni varia in funzione della distanza della molecola che stiamo studiando rispetto il pistone. Non varia però la frequenza di oscillazione. Si può infatti classificazione i sistemi acustici nella famiglia dei sistemi lineari. Un sistema si dice lineare se ad esso è applicabile il principio di sovrapposizione degli effetti. In ambito acustico, ciò vuol dire che se noi applichiamo ad un sistema una eccitazione che è combinazione lineare di frequenze singole, in uscita da tale sistema abbiamo una risposta che è combinazione lineare delle risposte delle singole componenti frequenziali. Si può dimostrare che se noi applichiamo un impulso sonoro contenente una unica frequenza, in uscita, può cambiare ampiezza e fase di tale impulso ma frequenza rimane la stessa dell'eccitazione.
Pressione e velocità: analogia col pendolo semplice.
Per capire la relazione tra velocità e pressione si deve pensare all'analogia col caso fisico del pendolo. Nel pendolo la massa in oscillazione trova lungo il suo percorso, punti nei quali quando la sua energia cinetica è massima, l'energia potenziale è nulla e quando è massima l'energia potenziale la velocità è nulla. In assenza di attriti o altre perturbazioni esterne il pendolo presenta una oscillazione senza fine. Per il principio di conservazione dell'energia si spiega anche la continua conversione da energia cinetica a potenziale e viceversa negli spostamenti del pendolo.

Figura 7 Pendolo semplice, descrizione qualitativa dell'andamento dell'energia cinetica ed energia potenziale della massa.
Allo stesso modo nello studio dei fenomeni acustici, in assenza di perturbazioni esterne, si ha una continua mutazione di energia delle singole particelle d'aria da cinetica a potenziale e viceversa. Come si nota bene dalla figura 8 ci sono punti dello spazio di propagazione del suono in cui le particelle d'aria ad un determinato istante di tempo, hanno velocità nulla. L'energia di tali particelle però è immagazzinata in forma potenziale e come effetto di ciò si ha un valore di massimo o minimo relativo della pressione dell'aria rispetto alla pressione atmosferica. Analogamente in altri punti in cui la pressione di annulla, la velocità delle particelle assume, in modulo, il valore di massimo relativo. Il grafico di fig. 8 evidenzia una proprietà fondamentale dei sistemi acustici: gli andamenti di pressione e velocità sono generalmente sfasati di un angolo ![]() . Nella fig.8 è mostrato il caso in cui lo sfasamento è pari a novanta gradi.
. Nella fig.8 è mostrato il caso in cui lo sfasamento è pari a novanta gradi.

Figura 8 Andamento della velocità e della pressione di particelle d'aria in funzione dello spazio, fissato l'istante di tempo.
A tal proposito è significativo sottolineare una interessante analogia tra la propagazione acustica attraverso un mezzo elastico - massivo e la propagazione di una corrente alternata in un circuito elettrico. In questo infatti facendo viaggiare corrente si hanno due grandezze imprescindibili: la tensione V e la corrente I. Si può giungere alla conclusione che la pressione in acustica sta alla tensione in elettrotecnica come la velocità sta alla corrente. Infatti se la situazione è come quella rappresentata in figura 8 cioè quando la pressione è in modulo massima, la velocità è nulla ho un trasferimento di energia sonora nulla. Per essere più chiari, questo sarebbe il caso di un onda stazionaria cioè un sistema dove energia c'è ma oscilla periodicamente nelle due forme che abbiamo più volte detto. Di questo argomento parleremo più aventi introducendo poi il concetto di impedenza sonora.
La grande potenzialità del suono è quella di avere una fortissima capacità informativa senza una grossa spesa energetica. Abbiamo infatti visto le variazioni di pressione necessarie per la propagazione del suono sono dell'ordine del decimo del Pascal o del Pascal stesso, molto inferiori rispetto al valore della pressione atmosferica pari a 101325 Pa. Inoltre il suono ha la proprietà di essere un genere di propagazione non dispersiva, questo perché le forma d'onda ossia l'informazione trasportata rimane immutata anche per distanze anche chilometriche.
Nello studio dei fenomeni acustici, si può incominciare a trattare quei suoni definiti PURI, cioè quei suoni periodici caratterizzati da un andamento sinusoidale del valore della pressione nello spazio in cui il suono si propaga. Tale periodicità della pressione non avverrà attorno un valore di 0 Pa, ma attorno al valore della pressione atmosferica pari a 101325 Pa.
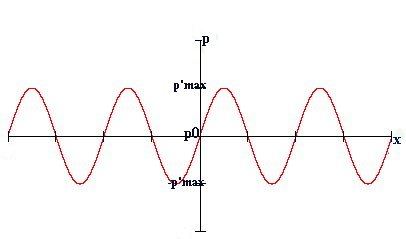
Le grandezze fondamentali per lo studio di tali suoni sono:
![]() (4)
(4)
pari al numero di giri al secondo dell'albero motore di figura 3. L'unità di misura è l'Hertz.
![]() (5)
(5)
L'unita di misura è naturalmente il secondo.
In campo sono la distanza che intercorre tra due successive compressioni, o rarefazioni, è definita lunghezza d'onda ![]() del suono nel mezzo considerato; la situazione del campo sonoro ad un certo istante può essere rappresentata mediante il grafico di figura 9 dove in ordinata sono riportate le variazioni della pressione in funzione della distanza perturbata; con
del suono nel mezzo considerato; la situazione del campo sonoro ad un certo istante può essere rappresentata mediante il grafico di figura 9 dove in ordinata sono riportate le variazioni della pressione in funzione della distanza perturbata; con ![]() si indica l'ampiezza ovvero il valore massimo della variazione di pressione.
si indica l'ampiezza ovvero il valore massimo della variazione di pressione.
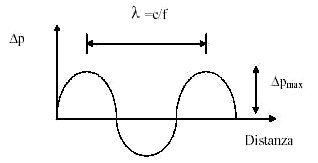
Figura 9 Suono sinusoidale: variazione della pressione in funzione della distanza. Rappresentazione della lunghezza d'onda.
Analogamente la situazione del campo sonoro può essere analizzata osservando come varia la pressione in un punto in funzione del trascorrere del tempo: in tal caso graficamente il fenomeno è del tutto analogo a quello riportato in fig. 9, ma avendo questa volta in ascissa il tempo ed in luogo della lunghezza d'onda il periodo T, tempo necessario per compiere un ciclo, ovvero l'intervallo di tempo che passa tra due istanti consecutivi nei quali, nel punto considerato, si ha un massimo od un minimo relativo di pressione.
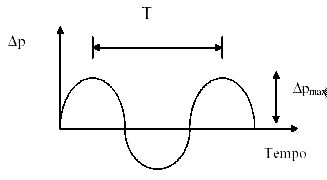
Figura 10 Tono puro sinusoidale : variazione in funzione del tempo.
La relazione che lega la velocità di propagazione c del suono nel mezzo alla lunghezza d'onda ![]() ed alla frequenza f è la seguente:
ed alla frequenza f è la seguente:
![]() (6)
(6)
Nel nomogramma di figura 10 è visualizzato il rapporto che intercorre tra ![]() e f.
e f.

Figura 11 Nomogramma lunghezza d'onda - frequenza.
L'aumento della frequenza diminuisce la lunghezza d'onda e viceversa; le relazioni appena scritte hanno una grande rilevanza pratica. Si consideri un cubo di spigolo pari ad 1 metro innanzi al quale è posta una sorgente sonora. Le dimensioni dell'onda ad alte frequenze divengono trascurabili rispetto a quelle del cubo il quale costituisce un ostacolo alla propagazione sonora.
Facciamo alcuni esempi: per f=20000Hz ![]()
![]() ho dimensioni irrisorie rispetto a quelle del cubo che quindi oscurerà l'onda acustica;
ho dimensioni irrisorie rispetto a quelle del cubo che quindi oscurerà l'onda acustica;
f=1000Hz ![]() questa è una situazione ibrida, infatti dietro al mio cubo si formeranno complessi fenomeni d'interferenza;
questa è una situazione ibrida, infatti dietro al mio cubo si formeranno complessi fenomeni d'interferenza;
infine per f=20Hz![]() questa volta sono le dimensioni dell'ostacolo ad essere trascurabili rispetto a quelle dell'onda.
questa volta sono le dimensioni dell'ostacolo ad essere trascurabili rispetto a quelle dell'onda.
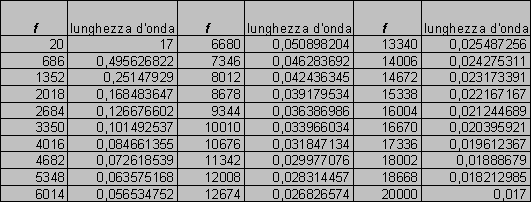
Figura 12 La tabella compilata con un foglio di calcolo riporta la lunghezza d'onda corrispondente ad una certa frequenza quando il mezzo propagante è l'aria.

Figura 13 Il grafico ottenuto interpolando i dati dell'andamento della lunghezza d'onda in funzione della frequenza.
Per comprendere meglio i concetti che esprimeremo consideriamo nuovamente il cilindro di fig. 3, in cui si muove il pistone e prendiamo un punto di ascolto al suo interno alla distanza D dal pistone; è ovvio pensare che la legge del moto delle particelle in tale punto sia a meno di un ritardo uguale a quella delle particelle che aderiscono al pistone. Tale ritardo è dovuto al tempo che l'onda acustica impiega per raggiungere l'orecchio dell'ascoltatore posto alla distanza D dalla sorgente, quindi in tale punto la legge del moto sarà:
![]() (7)
(7)
dove D rappresenta lo spazio che l'onda deve percorrere e c è la velocità di propagazione del suono. Il loro rapporto rappresenta il tempo di ritardo.
Il rapporto
![]() (8)
(8)
è una nuova quantità che chiamiamo numero d'onda e indichiamo con la lettera k.
L'unità di misura è il ![]() .
.
La formula (7) può essere riscritta allora come:
![]() (9)
(9)
dove ![]() è la pulsazione dell'oscillazione, pari al numero di giri al secondo dell'albero motore espresso in radianti.
è la pulsazione dell'oscillazione, pari al numero di giri al secondo dell'albero motore espresso in radianti.
Con tali accorgimenti, possiamo dire che la stessa pressione e la stessa velocità delle particelle del mezzo, possono essere viste come onde che si propagano nel cilindro. Possiamo quindi scrivere analogamente e con i dovuti accorgimenti di carattere dimensionale:
![]() (10)
(10)
![]() (11)
(11)
Come abbiamo già detto il ritardo
![]() (12)
(12)
nella formula (7) rappresenta il tempo impiegato dall'onda a raggiungere l'ascoltatore. Tale ritardo può essere anche molto dannoso; per esempio, nell'organizzazione di una orchestra sinfonica si deve tenere conto della distanza del direttore d'orchestra rispetto ai musicisti. Se tale distanza è troppo grande il suono giungerà alla platea di ascoltatori sfasato rispetto al tempo battuto dal direttore d'orchestra. Questo ritardo, è dovuto al fatto che, qualunque sia il mezzo nel quale il suono si propaga, la sua velocità di propagazione avrà sempre un valore finito. Per l'aria la velocità di propagazione del suono è stata stimata essere 340 m/s, valore molto alto rispetto alle velocità che caratterizzano la nostra vita e i nostri spostamenti, però ancora basso per un trasporto di informazioni a distanze chilometriche. Infatti supponendo l'assenza di fenomeni dissipativi, il suono impiega un secondo per percorrere 340m e impiegherebbe minuti ed ore se lo volessimo impiegare come ipotetico mezzo di comunicazioni tra parti diverse del globo terrestre.
Di notevole interesse è inoltre la relazione che lega la velocità di propagazione di un suono in un mezzo elastico - massivo alla temperatura. Riferendosi a relazioni ricavate nello studio della termodinamica, sotto le ipotesi di approssimare l'aria come un gas perfetto, si giunge alla importante relazione
![]() (13)
(13)
dove ![]() è un particolare coefficiente definito come il rapporto tra il calore specifico a pressione costante e il calore specifico a volume costante del mezzo in cui si propaga il suono,
è un particolare coefficiente definito come il rapporto tra il calore specifico a pressione costante e il calore specifico a volume costante del mezzo in cui si propaga il suono, ![]() è la costante di Boltzman, e
è la costante di Boltzman, e ![]() è la temperatura del mezzo misurata in gradi Kelvin. Numericamente per l'aria, la velocità del suono vale 340 m/s.
è la temperatura del mezzo misurata in gradi Kelvin. Numericamente per l'aria, la velocità del suono vale 340 m/s.
Da queste considerazioni e dalle proprietà dei materiali in relazione alla attitudine di trasmettere suoni si può introdurre il concetto di Impedenza acustica. Se la propagazione avviene senza sfasamento tra pressione e velocità di oscillazione delle particelle (ossia è nullo il ![]() nella formula (11)) si può definire impedenza acustica di un generico materiale il prodotto della sua densità
nella formula (11)) si può definire impedenza acustica di un generico materiale il prodotto della sua densità ![]() per la velocità di propagazione longitudinale del suono
per la velocità di propagazione longitudinale del suono ![]() nel materiale stesso (espressa in rayl).
nel materiale stesso (espressa in rayl).
Per l'aria, essendo la sua densità, in condizioni di temperatura 20°C ed alla pressione atmosferica di 1.013 bar , e la velocità di propagazione pari a circa 340 m/s, l'impedenza vale circa 400 rayl.
![]()
Nel caso in cui si presenti durante la propagazione di un'onda sonora in un materiale uno sfasamento ![]() non nullo tra la velocità di oscillazione e la pressione si può dare all'impedenza sonora, il cui simbolo è z, un'altra definizione; scrivendo la formula (10) come
non nullo tra la velocità di oscillazione e la pressione si può dare all'impedenza sonora, il cui simbolo è z, un'altra definizione; scrivendo la formula (10) come
![]() (14)
(14)
e scrivendo la formula (11) come
![]() (15)
(15)
ricavate dalle formule di Eulero, si definisce impedenza acustica il rapporto
![]() (16)
(16)
tale grandezza è nella sua forma più generale una grandezza complessa e si può anche scrivere nella forma:
![]() (17)
(17)
come somma della parte reale di z e di i-volte la parte immaginaria di z.
Nella tabella seguente sono riportati i valori dell'impedenza acustica per alcuni tipi di materiali, dalla quale si rileva la differenza esistente tra i valori dei mezzi aeriformi rispetto a quella notevolmente più elevata, dei mezzi solidi.
|
Materiale |
C(m/s) |
|
Z(rayl) |
Materiale |
c(m/s) |
|
Z(rayl) |
|
Metalli |
|
|
|
Legno nel senso della fibra |
|
|
|
|
Acciaio |
5000 |
7800 |
390 |
Abete |
4640 |
450 |
20.8 |
|
Argento |
5100 |
2700 |
138 |
Acero |
4110 |
670 |
27.8 |
|
Nickel |
4970 |
8700 |
430 |
Faggio |
3340 |
750 |
25 |
|
Oro |
2000 |
19300 |
386 |
Frassino |
4670 |
700 |
32.7 |
|
Ottone |
3500 |
8400 |
295 |
Olmo |
4120 |
570 |
23.4 |
|
Piombo |
1220 |
11400 |
138 |
Pino |
3320 |
500 |
16.6 |
|
Platino |
2650 |
21400 |
572 |
Pioppo |
4280 |
370 |
15.9 |
|
Rame |
3560 |
8900 |
317 |
Quercia |
3850 |
800 |
30.7 |
|
Stagno |
2500 |
7300 |
182 |
Idem trasv. alla fibra |
Valori ridotti di 1/3 |
|
|
|
Zinco |
3700 |
7000 |
259 |
|
|
|
|
|
Non metalli |
|
|
|
Liquidi |
|
|
|
|
Ardesia |
4500 |
3000 |
135 |
Acqua a 13°C |
1441 |
1000 |
14.4 |
|
Avorio |
3010 |
1800 |
54 |
Alcool |
1240 |
800 |
9.9 |
|
Gomma |
54 |
1000 |
0.54 |
Benzina |
1166 |
900 |
10.5 |
|
Non metalli |
|
|
|
Gas |
|
|
|
|
Granito |
3950 |
2700 |
107 |
Aria a 0°C |
331 |
1.3 |
4.27e-3 |
|
Marmo |
3810 |
2700 |
103 |
Aria a 15°C |
341 |
1.21 |
4.11e-3 |
|
Mattone |
3650 |
1800 |
66 |
Azoto |
336 |
1.25 |
4.2e-3 |
|
Vetro |
5500 |
2600 |
142 |
Ossigeno |
317 |
1.43 |
4.5e-3 |
|
Sughero |
500 |
240 |
1.2 |
Idrogeno |
1269 |
0.09 |
1.1e-3 |
Osservando la tabella si rileva come vi sia una stretta relazione tra densità e velocità di propagazione del suono nello stesso mezzo: in generale i materiali solidi, essendo dotati di maggiore densità, sono in grado di trasmettere più velocemente i suoni essendo evidentemente le particelle più a stretto contatto tra di loro; tuttavia avendo una impedenza acustica più elevata a parità di velocità di vibrazione delle loro particelle, necessitano una maggiore quantità di energia rispetto ai gas e ai liquidi. L'impedenza acustica è così fisicamente analoga all'impedenza elettrica.
Infatti, nel caso particolare di sfasamento nullo tra pressione e velocità si possono scrivere ancora le seguenti relazioni:
![]() (18)
(18)
e anche
![]() (19)
(19)
(Legge di Ohm acustica, per analogia alla legge di Ohm elettrica)
dove ![]() è la velocità di oscillazione delle particelle, p è la pressione,
è la velocità di oscillazione delle particelle, p è la pressione, ![]() è la velocità di propagazione nel mezzo e
è la velocità di propagazione nel mezzo e ![]() è la densità del mezzo stesso.
è la densità del mezzo stesso.
Principali Grandezze Acustiche di tipo energetico
.La quantità di energia irradiata da una sorgente sonora nell'unità di tempo è denominata potenza sonora ![]() . La potenza sonora
. La potenza sonora ![]() emessa da una sorgente è irradiata nel mezzo elastico, come l'aria, attraverso una determinata superficie S (o fronte d'onda) come lavoro dovuto al prodotto della forza di pressione p per la velocità di spostamento delle particelle v intorno al punto di equilibrio.
emessa da una sorgente è irradiata nel mezzo elastico, come l'aria, attraverso una determinata superficie S (o fronte d'onda) come lavoro dovuto al prodotto della forza di pressione p per la velocità di spostamento delle particelle v intorno al punto di equilibrio.
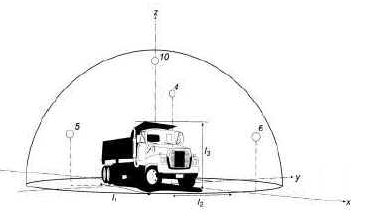
Figura 14 Uno dei possibili fronti d'onda per il calcolo della potenza sonora dissipata da un camion.
Con riferimento al modello di generazione sonora che ha portato alla formulazione delle relazioni (18) e (19), la potenza sonora ![]() può quindi essere correlata alla pressione sonora dall'equazione:
può quindi essere correlata alla pressione sonora dall'equazione:
![]() (20)
(20)
Per una sorgente che irradia uniformemente in tutte le direzione (mezzo isotropo), ovvero in campo libero, il fornte d'onda S è pari alla superficie di una sfera (vedi figura 15 ); alla distanza r dalla sorgente la potenza sonora sarà dunque pari a:
![]() (21)
(21)
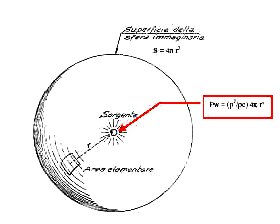
Figura 15 Potenza sonora di una sorgente nello spazio.
Nella pratica le sorgenti sonore irradiano con potenze estremamente variabili che vanno dal valore della voce umana a livello di conversazione, pari circa a ![]() , al rumore di un turbogetto pari a
, al rumore di un turbogetto pari a ![]() . (Vedi tabella sottostante).
. (Vedi tabella sottostante).
Tabella 2: Tipici valori della potenza sonora di alcune sorgenti.
|
sorgente |
Aereo turbogetto |
aereo turboelica |
Orchestra (75 elem.) |
Martello pneumatico |
Radio alto volume |
Auto in autostrada |
|
Potenza (W) |
|
|
|
1 |
|
|
|
sorgente |
Ventilatore Assiale (1500 giri/l'ora) |
Conversazione normale |
sussurro |
|
Potenza (W) |
|
|
|
Sia ![]() la potenza sonora irradiata da una sorgente su un fronte d'onda S, nel caso di campo libero sussiste la seguente relazione tra potenza sonora e intensità sonora I:
la potenza sonora irradiata da una sorgente su un fronte d'onda S, nel caso di campo libero sussiste la seguente relazione tra potenza sonora e intensità sonora I:
![]() (22)
(22)
e quindi l'intensità è definita come l'energia che, nell'unità di tempo, fluisce attraverso l'unità di area del fronte d'onda. La relazione (22) è scritta semplificata al caso in cui il fronte d'onda è costituito da una sfera di raggio r.
Una definizione più rigorosa e più complessa può essere la seguente:
L'intensità acustica è una grandezza di natura vettoriale a cui corrisponde una densità di flusso di energia per unità di tempo. Essa è determinata dal prodotto della pressione acustica e della velocità delle particelle oscillanti attorno alla loro posizione di equilibrio:
![]() (23)
(23)
Fissando un punto nello spazio, per un'onda sonora di pulsazione ![]() , la pressione può essere identificata da
, la pressione può essere identificata da
![]() (24)
(24)
e la velocità di oscillazione delle particelle dal vettore
![]() , (25)
, (25)
essendo ![]() lo sfasamento tra pressione e velocità. Allora l'intensità definita da (23) diventa
lo sfasamento tra pressione e velocità. Allora l'intensità definita da (23) diventa
![]() (26)
(26)
utilizzando le formule di addizione del coseno.
Il primo termine della differenza della formula (26) è detto l'intensità attiva istantanea ![]()
![]() , e descrive l'energia trasferita e trasmessa dal mezzo. Esso è il termine in cui la pressione e la velocità sono in fase.
, e descrive l'energia trasferita e trasmessa dal mezzo. Esso è il termine in cui la pressione e la velocità sono in fase.
Il secondo termine detto intensità reattiva istantanea ![]() , corrisponde ad una oscillazione di energia il cui valor medio temporale in ogni periodo è nullo.
, corrisponde ad una oscillazione di energia il cui valor medio temporale in ogni periodo è nullo.
![]() (27)
(27)
![]() (28)
(28)
Il valore di intensità più comunemente utilizzato è l'intensità media come media temporale del valore istantaneo.
![]() (29)
(29)
E' molto forte in questo studio, l'analogia con l'elettrotecnica nell'analisi della potenza elettrica in circuiti in regime alternato. Anche in quel argomento la potenza elettrica media come media temporale della potenza elettrica istantanea era scritta come:
![]() (30)
(30)
Ritornando nell'ambito acustico, in campo libero, ossia quando lo sfasamento tra pressione e velocità è nullo, le complesse relazioni di prima si semplificano notevolmente, e grazie alla nozione di impedenza acustica si può scrivere:
![]() (31)
(31)
e per la (22) risulta che la pressione sonora è così legata alla potenza :
![]() (32)
(32)
In un'onda piana invece la superficie del fronte d'onda rimane costante (ad es. nel rumore generato da un elettroventilatore all'interno di un condotto a sezione costante) e se non vi sono dissipazioni sulle pareti del condotto (ad es. materiale fonoassorbente), l'intensità non varia all'aumentare della distanza. La relazione più generale tra potenza ed intensità è insita nella definizione di quest'ultima: "potenza per unità di superficie", è quindi possibile determinare la potenza emessa da una o più sorgenti poste all'interno di una superficie chiusa, integrando nello spazio l'intensità misurata sulla superficie:
![]() (33)
(33)
Mentre la relazione Potenza - Intensità è valida in un qualsiasi tipo di campo acustico, non è invece derivabile un'espressione diretta che leghi Potenza - Pressione, salvo che per il caso già considerato di campo libero. (Formula (32)).
Per capirne la problematica si deve prestare attenzione al fatto che mentre l'Intensità rappresenta molto semplicemente la Potenza acustica di una sorgente distribuita sulla superficie di emissione, la Pressione è una conseguenza del moto vibrazionale e dipende dalla Potenza acustica della sorgente e da altri parametri più complessi e variabili, come la Direzionalità dell'emissione, dall'ambiente circostante, e varie altre situazioni al contorno. L'analogia del "discorso acustico" potrebbe essere fatta con quello termico: una stufa elettrica è la sorgente di potenza termica in grado di riscaldare l'ambiente, ed il "grado" di riscaldamento viene determinato con una misura di temperatura, la stessa stufa posta in un atro ambiente, mantiene la stessa potenza termica ma la temperatura di questo ambiente non sarà necessariamente la stessa del precedente, in quanto intervengono fattori come il volume dell'ambiente e il grado di isolamento termico delle pareti. La misura della temperatura è infatti corrispondente alla misura di Pressione acustica, essa dipende dal volume dell'ambiente e dalle caratteristiche fonoassorbenti delle pareti che lo delimitano.