Argomenti trattati
Esercizi sul moto dei fluidi
· Esercizio n° 1 e 2 – Esempi di ciclo iterativo
· Esercizio n° 3 – Lo svuotamento di due serbatoi
· Esercizio n° 4 – La fontana
Appendice
· Diagramma di Moody
·
Nomogramma
·
Coefficiente Beta per alcune accidentalità presenti in
un circuito idraulico
Esercizi sul moto dei fluidi
Esercizio n° 1 – Esempi di ciclo iterativo
Testo
In un tubo orizzontale di
diametro D=15cm e lunghezza L=300m scorre acqua con una portata ![]() 1800 l/min ad una temperatura di 27° C.
1800 l/min ad una temperatura di 27° C.
Calcolare quanto varia la portata se l’acqua viene
raffreddata fino a 5° C considerando che la potenza della pompa è costante (![]() =costante)(coeff. di rendimento
=costante)(coeff. di rendimento ![]() ).
).
Dati
L = 300 m
![]() =costante
=costante
![]() =1800 l/min
=1800 l/min
![]()
![]() ° C
° C
![]() = 5° C
= 5° C
D =15 cm
![]()
![]()
Soluzione
Ricaviamo dapprima la viscosità cinematica ![]() dal rapporto tra
la viscosità statica
dal rapporto tra
la viscosità statica ![]() e la densità
dell’acqua
e la densità
dell’acqua ![]() , i cui valori sono stati ottenuti su tabelle apposite
considerando il liquido alla temperatura di 27° C e alla pressione di 1 BAR.
, i cui valori sono stati ottenuti su tabelle apposite
considerando il liquido alla temperatura di 27° C e alla pressione di 1 BAR.
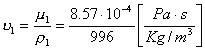
![]()
Ora calcoliamo il numero di Reynolds per risalire, tramite il diagramma di Moody, al
fattore di attrito ![]() e comprendere
anche sotto quale tipo di regime ci troviamo (laminare, di transizione o
turbolento).
e comprendere
anche sotto quale tipo di regime ci troviamo (laminare, di transizione o
turbolento).
Per determinare la velocità del fluido dividiamo la portata per la sezione del tubo:

![]()
Determinato il valore (siamo in regime fortemente
turbolento) possiamo, conoscendo la scabrezza relativa ![]() , valutare il fattore
di attrito
, valutare il fattore
di attrito ![]() avvalendoci del
diagramma di Moody.
avvalendoci del
diagramma di Moody.
Otteniamo così ![]() =0.0145
=0.0145
Calcoliamo le perdite distribuite:
![]()
Dunque la potenza della pompa è:
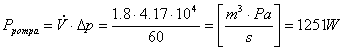
Dato che la pompa ha un rendimento ![]() , la potenza effettiva risulta:
, la potenza effettiva risulta:
![]()
Se riduco la temperatura avrò delle variazioni nei
valori della viscosità e quindi nel numero di Reynolds, mentre per ipotesi,
terrò la velocità ![]() costante.
costante.
![]()
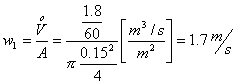
Quindi avrò
![]()
e consultando il diagramma di Moody mantenendo il precedente
valore di scabrezza relativa ![]() e utilizzando il
nuovo numero di Reynolds, ottengo:
e utilizzando il
nuovo numero di Reynolds, ottengo:
![]()
Il fattore di attrito è aumentato(Reynolds invece è diminuito) e, poiché abbiamo supposto costante la potenza della pompa, deve essere calata la portata. Se è calata la portata, però dovrà diminuire anche la velocità che in un primo momento avevamo supposto costante.
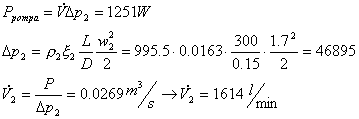
La velocità sarà ![]()
Ricalcolando i vari coefficienti e parametri dovrò ora tenere la nuova velocità.
Ottengo:
![]()
![]()
![]()
![]()
Ma la nuova portata varrà:
![]()
Il processo iterativo non converge per cui adesso provo a mantenere costante la prevalenza e non più la velocità.
![]()
![]()
![]()
 =
=
=![]()
e calcolo la nuova portata:
![]()
la nuova prevalenza sarà, dovendo essere la potenza costante:
![]()
adesso utilizzo la nuova prevalenza per iterare ulteriormente calcolando il nuovo numero di Reynolds, la nuova velocità e un’ulteriore prevalenza:
![]()
![]()
il nuovo valore della velocità sarà:

mentre quello della portata:
![]()
e calcolando la prevalenza otteniamo un valore prossimo a quello definitivo:
![]()

Esercizio n° 2 – Esempi di ciclo iterativo
Testo
Due tubi orizzontali (1 e 2)
posti in serie, di diametro rispettivamente ![]() =5cm e
=5cm e ![]() =10cm e lunghezza
=10cm e lunghezza ![]() =180m e
=180m e ![]() =90m collegano due serbatoi riempiti con acqua (la differenza
di quota tra i due peli liberi vale
=90m collegano due serbatoi riempiti con acqua (la differenza
di quota tra i due peli liberi vale ![]() =6m). Sapendo che i tubi sono in ghisa con un
=6m). Sapendo che i tubi sono in ghisa con un ![]() =0.2mm e considerando un coefficiente di viscosità cinematica
=0.2mm e considerando un coefficiente di viscosità cinematica
![]() , calcolare la portata in volume di acqua tra i due serbatoi.
, calcolare la portata in volume di acqua tra i due serbatoi.
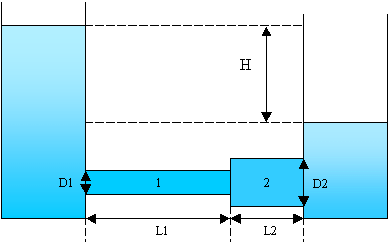
Dati
![]() =180m
=180m
![]() =90m
=90m
![]() =5cm
=5cm
![]() =10cm
=10cm
H=6m
![]()
Soluzione
Per cominciare scriviamo la legge di Bernoulli applicata alle due sezioni:
![]()
![]()
![]()
in cui il primo termine è stato troncato perché le velocità sono molto piccole e quindi trascurabili mentre il secondo termine è barrato poiché il salto di pressione è nullo in soli 6m di dislivello.
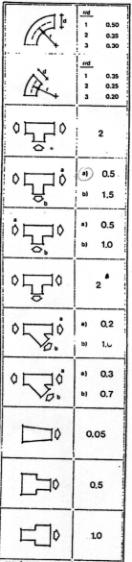
Calcolo adesso le perdite concentrate e distribuite avvalendomi della lunghezza equivalente ricavata dalla consultazione del nomogramma in appendice.
![]() (1)
(1)
ma la portata deve essere la
stessa nelle due sezioni:
![]()
allora:
![]()
Sostituiamo ![]() nella (1) e
otteniamo:
nella (1) e
otteniamo:
![]()
ricaviamo allora ![]() :
:
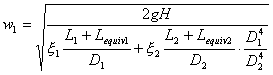 (2)
(2)
Nell’equazione (1) sono presenti tre incognite (la velocità
![]() ed i fattori
d’attrito
ed i fattori
d’attrito ![]() e
e ![]() ). Poiché i fattori di attrito dipendono dalla velocità tramite
il numero di Reynolds, risolveremo il problema innescando un ciclo iterativo e
considerando una
). Poiché i fattori di attrito dipendono dalla velocità tramite
il numero di Reynolds, risolveremo il problema innescando un ciclo iterativo e
considerando una ![]() che chiameremo
“velocità di primo tentativo.
che chiameremo
“velocità di primo tentativo.
·
Primo tentativo
![]()
![]()

Ora calcolo i numeri di Reynolds corrispondenti:
![]()
![]()
Calcolo adesso la scabrezza relativa dei tubi in ghisa:
![]()
![]()
Considerando i valori appena calcolati (numeri di Reynolds
e scabrezza relativa), consultiamo il diagramma di Moody per risalire ai
coefficienti di attrito ![]() e
e ![]() .
.
Abbiamo:
![]()
![]()
Ricaviamo facilmente le lunghezze equivalenti consultando
il Nomogramma: alla voce allargamento brusco di sezione ![]() corrisponde il punto
13 del diagramma mentre alla voce allargamento brusco di diametro
corrisponde il punto
13 del diagramma mentre alla voce allargamento brusco di diametro ![]() corrisponde il punto
10. Otteniamo:
corrisponde il punto
10. Otteniamo:
![]()
![]()
Sostituiamo i valori nella (2) e
avremo:

· Secondo tentativo
![]()
![]()
![]()
E ricalcoliamo Reynolds:
![]()
![]()
A cui corrispondono rispettivamente:
![]()
![]()
Sostituiamo quindi nella (2)
ottenendo:

L’iterazione
potrebbe continuare ma otterremmo risultati di valore analogo. Siamo giunti ad
una buona approssimazione del risultato reale.
Esercizio n° 3 – Lo svuotamento di due serbatoi
Testo
A due serbatoi uguali di forma
cilindrica (A e B) di diametro D=1m riempiti di acqua (![]() ), sono stati
applicati alla base due condotti di lunghezza diversa (rispettivamente
), sono stati
applicati alla base due condotti di lunghezza diversa (rispettivamente ![]() e
e ![]() con
con ![]() ) e diametro d=100mm. Determinare quale dei due serbatoi si
svuota per primo.
) e diametro d=100mm. Determinare quale dei due serbatoi si
svuota per primo.
Dati
![]()
![]()
![]()
![]()
![]()
![]()
D=1m
d=100mm
![]()
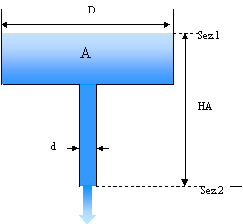
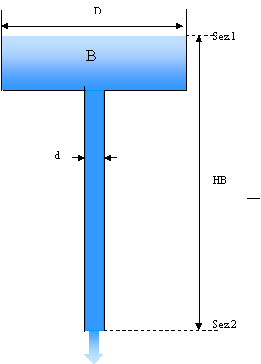
Soluzione
Calcoliamo le perdite di carico concentrate e distribuite:
![]()
![]()
![]()
in cui L è la lunghezza del
condotto mentre ![]() è la velocità nella sezione 2.
è la velocità nella sezione 2.
Applico l’equazione di Bernoulli di bilancio dell’energia:
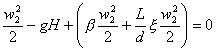
esplicitando ![]() :
:
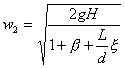
Supponiamo che la lunghezza del
tubo L sia circa uguale ad H (![]() ).
).
Notiamo che la
velocità con cui esce l’acqua dipende dal fattore d’attrito, che a sua volta
dipende dalla stessa ![]() ; dunque è necessario procedere tramite un ciclo iterativo.
Ipotizzo di trascurare le perdite distribuite ponendo
; dunque è necessario procedere tramite un ciclo iterativo.
Ipotizzo di trascurare le perdite distribuite ponendo ![]() (questo permette di
considerare il condotto liscio).
(questo permette di
considerare il condotto liscio).
![]() (velocità di primo
tentativo) =
(velocità di primo
tentativo) = ![]()
![]()
Dal diagramma di Moody,
considerando una scabrezza relativa ![]() ottengo
ottengo![]()
Da questo valore ricavo la velocità di secondo tentativo:
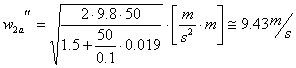
![]()
ottengo![]()
Da questo valore ricavo la velocità di terzo tentativo:

che può essere considerata il risultato definitivo.
Operando in modo analogo con il serbatoio B otteniamo:
![]()
![]()
Dal diagramma di Moody,
considerando una scabrezza relativa ![]() ottengo
ottengo![]()
Da questo valore ricavo la velocità di secondo tentativo:

![]()
ottengo![]()
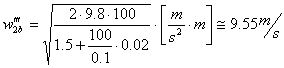
che è il nostro risultato definitivo.
Abbiamo dimostrato che B si svuota prima rispetto ad A.
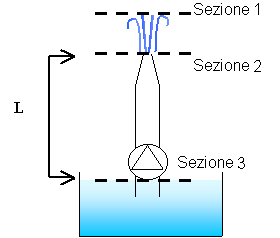
Esercizio n° 4 – La fontana
L = 6 m
Dp = 4 BAR = 4 x 105 Pa
D = 0.08 m
d = 0.02 m
e = 0.05 mm
r = 103 Kg/m3
u = m/r = 10-6 m2/s
Soluzione
Iniziamo a risolvere il problema
prendendo 2 sezioni nella fontana della figura a cui faremo riferimento nella
legge di Bernulli. Scegliamo una prima sezione all’altezza del pelo dell’acqua
nella fontana (sezione 3), mentre prendiamo la seconda sull’orifizio di
diametro d (sezione 2).
L’equazione di Bernoulli:
![]()
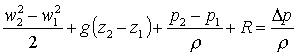 (1)
(1)
Il termine ![]() verrà tralasciato in
quanto le due sezioni scelte si trovano entrambe alla pressione atmosferica.
verrà tralasciato in
quanto le due sezioni scelte si trovano entrambe alla pressione atmosferica.
Abbiamo bisogno di un’ulteriore equazione per risolvere il sistema in 2 incognite. Sfruttiamo l’equazione di continuità uguagliando le portate nelle due sezioni:
![]() (2)
(2)
Poichè la sezione S = ![]() , otterremo
, otterremo 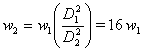
Risolviamo allora il sistema:
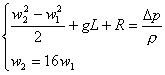 (3)
(3)
Consideriamo allora le perdite di carico.
Utilizzando il Nomogramma in appendice possiamo calcolare le perdite di carico
localizzate come perdite distribuite su una determinabile lunghezza
equivalente ![]() . Conoscendo il diametro interno del tubo (2 mm) e il numero
a cui corrisponde questa accidentalità (allargamento brusco di sezione
. Conoscendo il diametro interno del tubo (2 mm) e il numero
a cui corrisponde questa accidentalità (allargamento brusco di sezione ![]() ) è facile ricavarne il valore:
) è facile ricavarne il valore:
![]()
![]() 0.7
0.7
Troviamo adesso il valore delle perdite di carico
in funzione del coefficiente d’attrito ![]() :
:
![]() (4)
(4)
Sostituendo nel nostro sistema otteniamo una
seconda funzione ![]() di questo tipo:
di questo tipo:
![]() (5)
(5)
Il calcolo del fattore di attrito però, richiede la
conoscenza del numero di Reynolds Re e della velocità che individueranno
sul diagramma di Moody un determinato valore di ![]() . In questo caso non è possibile calcolare Re in
quanto esso stesso dipende dalla velocità w.
. In questo caso non è possibile calcolare Re in
quanto esso stesso dipende dalla velocità w.
Dunque utilizzeremo un procedimento iterativo. Per iniziare possiamo calcolare il valore di velocità che avremmo in presenza di un fattore di attrito nullo.
Quando ![]()
![]()
![]()
Questo valore di velocità ci porterebbe a calcolare il seguente numero di Reynolds:
![]() (6)
(6)
Siamo in presenza di moto turbolento. Con questo
determinato valore di Re e utilizzando la viscosità data ![]() leggiamo sul
diagramma di Moody un nuovo valore di
leggiamo sul
diagramma di Moody un nuovo valore di ![]() diverso dal
precedente che chiameremo
diverso dal
precedente che chiameremo ![]() .
.
Con questo nuovo coefficiente d’attrito calcoliamo
con la (5) una nuova velocità ![]() . Questo nuovo valore, che differisce di poco dal valore
precedente, posso considerarlo il mio valore definitivo.
. Questo nuovo valore, che differisce di poco dal valore
precedente, posso considerarlo il mio valore definitivo.
Infine, ritornando al sistema (3) calcolo la
velocità sulla seconda sezione: ![]() .
.
Prendo in considerazione le sezioni 2 e 3. La formula di Bernoulli si riduce ad un’equazione molto semplice. L’altezza raggiunta dal getto è:
![]()
Appendice
DIAGRAMMA DI MOODY
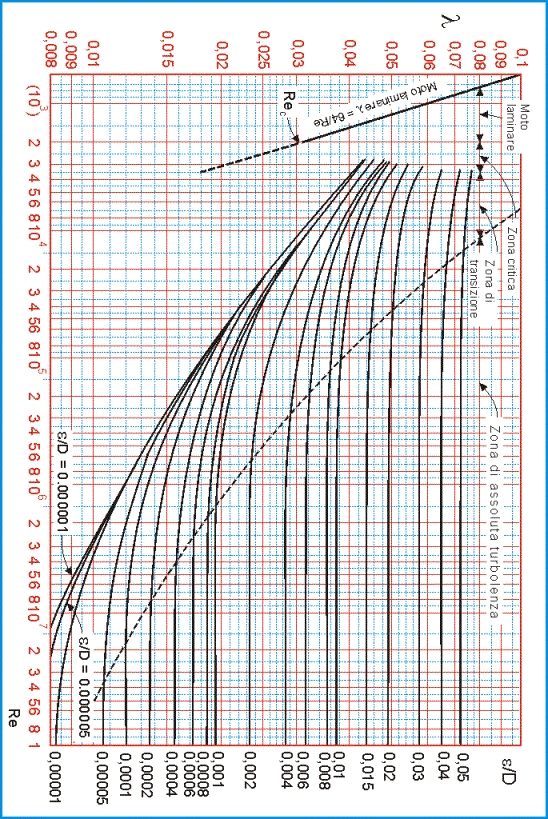
![]()
Nomogramma
 Accidentalità
Accidentalità
1.
Saracinesca aperta ¼”
2.
Valvola dritta aperta
3.
Saracinesca aperta ½”
4.
Valvola ad angolo aperta
(4’ - Filtro)
5.
Valvola di ritegno
aperta
6.
Raccordo curvo a 180°
7.
Raccordo a squadra a 90°
8.
Saracinesca aperta ¾”
9.
Raccordo curvo a 90°
raggio stretto
10.
Allargamento di sez. 1à 4
11.
Raccordo curvo a 90°
raggio medio
12.
Raccordo curvo a 90°
raggio medio
13.
Allargamento di sez. 1à 2
14.
Imbocco
15.
Raccordo curvo a 45°
16.
Restringimento di
sezione 4 à 1
17.
Saracinesca aperta 1”
18.
Saracinesca aperta 2”
Coefficiente Beta per alcune accidentalità
presenti in un circuito idraulico