 Quindi l’acqua scorre con un moto turbolento.
Quindi l’acqua scorre con un moto turbolento.Esercizio 1
Si consideri un condotto a sezione circolare dentro il quale scorre acqua ad una temperatura superiore di quella ambiente. Si vuole determinare il coefficiente di convezione interno.
Successivamente, nota la potenza termica scambiata, determinare la temperatura esterna della parete del condotto.
Dati del problema:
Soluzione
Per prima cosa bisogna sapere con quale tipo di moto l’acqua scorre all’interno del condotto, quindi calcoliamo il numero di Reynolds Re.
Essendo la viscosità dell’acqua pari a 5.10-6 m2/s ad una temperatura di 80 °C troviamo
 Quindi l’acqua scorre con un moto turbolento.
Quindi l’acqua scorre con un moto turbolento.
Calcoliamo ora il numero di Prandtl Pr:
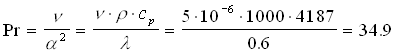 per arrivare al coefficiente di convezione calcoliamo il numero di Nusselt Nu con la formula di Dittus e Boelter (vedere tabella 2 dell’appendice):
per arrivare al coefficiente di convezione calcoliamo il numero di Nusselt Nu con la formula di Dittus e Boelter (vedere tabella 2 dell’appendice):
![]() e infine troviamo
e infine troviamo
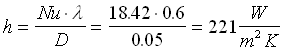
Supponiamo ora che la potenza termica scambiata sia Q = 207 W, allora la temperatura esterna della parete del condotto vale
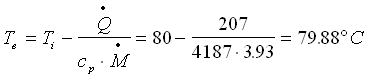 dove M rappresenta la portata in massa e vale
dove M rappresenta la portata in massa e vale
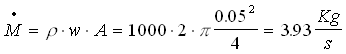
Esercizio 2 (Tiraggio di un camino naturale)
Si determini la temperatura esterna di un tubo di lamiera a sezione quadrata attraverso il quale si scaricano fumi caldi. Dati del problema:
Soluzione
Per lo svolgimento di questo problema useremo due equazioni che definiscono la potenza termica scambiata; dallo scambio termico si ottiene
![]()
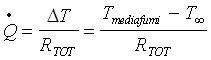 mentre da un bilancio dell’entalpia si ottiene
mentre da un bilancio dell’entalpia si ottiene
Ipotizziamo che il tubo sia rotondo perché ai fini pratici l’errore commesso è accettabile.
Ora passiamo allo studio della rete elettrica equivalente per determinare RTOT, che sarà composta dalla somma di tre contributi dovuti a tre resistenze diverse:
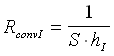 resistenza di convezione interna, che vale
resistenza di convezione interna, che vale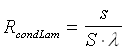 resistenza di conduzione della lamiera, che vale
resistenza di conduzione della lamiera, che vale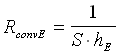 resistenza di convezione esterna, che vale
resistenza di convezione esterna, che vale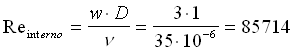 Determiniamo il coefficiente di convezione interno:
Determiniamo il coefficiente di convezione interno:
per cui all’interno del tubo abbiamo un regime turbolento, dalle tabelle sappiamo che il numero di Prandtl vale Pr = 0.71, quindi possiamo calcolare il numero di Nusselt con la formula di Dittus e Boelter (vedere tabella 2 dell’appendice):

![]() ed ora possiamo calcolare il coeff. hI:
ed ora possiamo calcolare il coeff. hI:
Ora dobbiamo calcolare il coefficiente di convezione esterno:
supponiamo che all’esterno del tubo ci sia convezione naturale, quindi calcoliamo il numero di Grashof Gr:
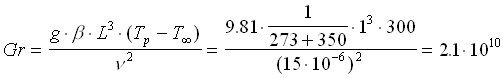 dove per Tp (incognita) è stato preso un valore "ragionevole" che verrà successivamente migliorato con successive approssimazioni: intendiamo infatti, una volta trovata la temperatura esterna della parete, sostituirla a Tp nella formula e iterare il processo fino ad un risultato con variazioni minime. Per la grandezza significativa L invece, abbiamo preso il diametro del tubo.
dove per Tp (incognita) è stato preso un valore "ragionevole" che verrà successivamente migliorato con successive approssimazioni: intendiamo infatti, una volta trovata la temperatura esterna della parete, sostituirla a Tp nella formula e iterare il processo fino ad un risultato con variazioni minime. Per la grandezza significativa L invece, abbiamo preso il diametro del tubo.
Il numero di Rayleigh vale:
![]() per cui il moto esterno è turbolento (aria che si muove per convezione forzata), quindi il numero di Nusselt Nu vale (vedi tabella 3 dell’appendice):
per cui il moto esterno è turbolento (aria che si muove per convezione forzata), quindi il numero di Nusselt Nu vale (vedi tabella 3 dell’appendice):
![]() Infine calcoliamo hE:
Infine calcoliamo hE:
Ora possiamo calcolare la resistenza termica totale  RTOT che vale:
RTOT che vale:
 dove S = D.L:p
= 15,7 m2.
dove S = D.L:p
= 15,7 m2.
La potenza termica scambiata vale
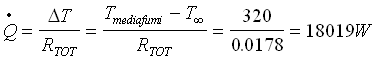 e la temperatura esterna della parete TOUT:
e la temperatura esterna della parete TOUT:
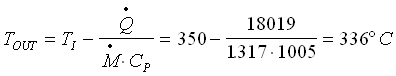 dove la portata in massa vale
dove la portata in massa vale
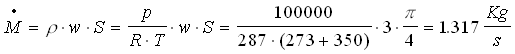
 Ora andiamo a ricalcolare il numero di Grashof Gr mettendo TOUT al posto di TP:
Ora andiamo a ricalcolare il numero di Grashof Gr mettendo TOUT al posto di TP:
quindi
Ra=Gr.Pr=2.36.1010.0.71=1.675.1010

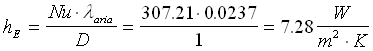 Nu=0.13.Gr0.33.Pr0.33=0.13.(2.35.1010)0.33.0.710.33=307.21
Nu=0.13.Gr0.33.Pr0.33=0.13.(2.35.1010)0.33.0.710.33=307.21
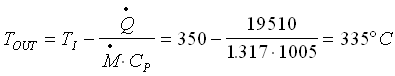
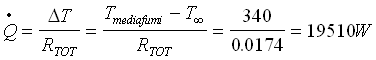 che prendiamo come risultato definitivo visto che la variazione rispetto a prima è stata minima.
che prendiamo come risultato definitivo visto che la variazione rispetto a prima è stata minima.
Convezione Forzata: casi particolari
Quando si vuole studiare un problema di convezione trascurando l’effetto delle forze di galleggiamento, è necessario porre b =0, per cui il numero delle variabili presenti nella (1)
Nu = f (r p , m , gb ,a 2 , L , W , ç Tp – Tf ç ) (1)
Nu = f (Re, Gr, Pr) (2)
passa da 8 a 7; conseguentemente, i numeri puri calano da 4 a 3 e quindi la (2) diviene:
Nu = f (Re, Pr) (3)
ed in prima approssimazione:
Nu = C . Rea . Prc (4)
Se il moto è laminare e stazionario, dall’equazione di continuità si deduce che per un fluido incomprimibile il moto è anche uniforme, vale a dire privo di accelerazioni. In queste condizioni il numero delle variabili si riduce ulteriormente, e con esso anche quello dei numeri puri: il numero di Nusselt risulta funzione del prodotto Re . Pr, anziché dei due numeri separatamente; in pratica significa avere nella (4) a = c.
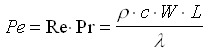 Il prodotto Re . Pr è noto anche come "numero di Péclet":
Il prodotto Re . Pr è noto anche come "numero di Péclet":
Fisicamente esso ha lo stesso significato di Nu, essendo il rapporto tra il calore trasportato per convezione e quello trasportato per conduzione attraverso uno strato di spessore L, a parità di differenza di temperatura.
Dall’esame della tabella 1 si può notare come, in tutti i casi considerati, in virtù delle condizioni di moto laminare e di profili dinamico e termico completamente sviluppati, si abbia sempre a = c = 0, per cui Nu assume un valore indipendente dalla natura del fluido e dalla sua velocità media.
Ciò non è più vero quando si considerano regioni di ingresso termico o addirittura dinamico e termico contemporaneamente: la soluzione di questa particolare categoria di problemi richiede la conoscenza di un parametro in più, vale a dire della distanza corrente tra il punto considerato e quello di inizio della regione di ingresso; assunto il diametro equivalente come lunghezza di riferimento, interviene quindi nel problema una seconda lunghezza X, per cui a fianco dei numeri puri già considerati comparirà anche il rapporto adimensionale D/X.
Nella tabella 2 sono stati raccolti alcuni valori ottenuti da diversi autori correlando risultati sperimentali propri o di altri, relativi a moto entro condotti, unitamente a quelli dedotti con due soluzioni teoriche. Tali valori sono accettabili con una approssimazione del 10 – 20%, per Pr > 0.5, e quindi per tutti i fluidi omogenei di comune impiego, esclusi i metalli allo stato liquido.
Convezione naturale o mista: casi particolari
Quando si vuole studiare un problema di convezione naturale pura, è necessario tener presente che il fluido assume velocità nulla non solo sulla parete ma anche a distanza infinita dalla stessa, quindi su tutto il contorno del sistema: pertanto scompare, tra le variabili presenti nella (1), la velocità media W. Riducendosi di uno il numero delle variabili, deve scomparire anche un numero puro; si perviene così alla relazione:
Nu = f (Gr, Pr) (5)
e all’espressione approssimata:
Nu = C . Grb . Prc (6)
Se pio il problema è di convezione naturale con moto privo di accelerazioni, scompare anche il valore della densità, analogamente a quanto visto nella convezione forzata: conseguentemente si ha nella (6) b = c.
Poiché il numero di Reynolds non interviene nella (6), è necessario disporre di un altro criterio per poter discernere tra moto laminare e moto turbolento; si definisce allora un nuovo numero puro, dato dal prodotto Gr . Pr e noto come "numero di Rayleigh": sperimentalmente si vede, per ordine di grandezza, che il moto laminare si verifica solo se Ra = Gr . Pr < 109.
Nella tabella 3 vengono riportati, a titolo di informazione, i valori delle costanti relativi ad alcuni tra i casi che sono studiati da diversi autori: come nel caso della tabella 2, i valori di h ottenibili con l’impiego delle relazioni in essa riportate devono essere considerati con una tolleranza del 10%.
Per farsi un’idea sul caso di convezione che si viene a dover trattare, in prima approssimazione si può considerare:
Tutto ciò deriva dal fatto che l’importanza del termine che tiene conto delle forze di galleggiamento nell’equazione del moto è condizionata dal valore numerico assunto dal raggruppamento adimensionale Gr / Re2. Con maggiore rigore scientifico, è stato predisposto da Eckert e Diaguila un grafico con il quale è possibile definire a priori i campi di influenza due fenomeni.
Appendice: Tabelle
|
Sezione del condotto |
Condizioni al contorno |
||
|
Flusso di calore alla parete = cost |
Temperatura della parete = cost |
||
|
Circolare |
4.36 |
3.66 |
|
|
Quadrata a = b |
3.63 |
2.98 |
|
|
Rettangolare |
a = 1.4 b |
3.73 |
3.08 |
|
a = 2 b |
4.11 |
3.40 |
|
|
a = 3 b |
4.79 |
3.96 |
|
|
a = 4 b |
5.35 |
4.44 |
|
|
a = 8 b |
6.49 |
5.60 |
|
|
a = ¥ |
8.24 |
7.54 |
|
|
a = ¥ con una superficie isolata |
5.38 |
4.86 |
|
|
Triangolare a = b = c |
3.11 |
2.47 |
|
Tabella 1 – Valori del numero di Nusselt per moto laminare e profili completamente sviluppati.
|
Campo di validita’ (Re) |
Regime |
Costante In parete |
Nu = C.Rea.Prc |
Autori |
Note |
|||||
|
Ingr. Dinamico |
Ingr. Termico |
Sviluppato |
T
|
Q |
C |
a |
c |
|||
|
< 2300 |
* |
* |
* |
0.289(D/X)1/2 |
0.5 |
0.33 |
Elser |
L < 20 D |
||
|
< 2300 |
* |
* |
1.86(D/X)1/3 |
0.33 |
0.33 |
Sieder e Tate |
X > 20 D |
|||
|
< 2300 |
* |
* |
* |
0.664(D/X)1/2 |
0.5 |
0.33 |
Pohlhaunsen |
|||
|
3000 – 30000 |
* |
* |
0.0033 |
1 |
0.37 |
Böhm |
||||
|
2700 – 7000 |
* |
* |
* |
0.01(D/X)0.37 |
1 |
0.37 |
Giulianini e altri |
1.2 D < X X < 20 D |
||
|
> 10000 |
* |
* |
0.036(D/X)1/18 |
0.8 |
0.33 |
Nusselt |
||||
|
> 10000 |
* |
0.032(D/X)1/20 |
0.8 |
0.37 |
Kraussold |
Liquido Riscaldato |
||||
|
> 10000 |
* |
0.032(D/X)1/20 |
0.8 |
0.3 |
Kraussold |
Liquido Raffreddato |
||||
|
> 10000 |
* |
0.183(D/X)1/3 |
7/12 |
0.33 |
Elser |
Teorico |
||||
|
> 10000 |
* |
* |
0.023 |
0.8 |
0.4 |
Dittus e Boelter |
Fluido Riscaldato |
|||
|
> 10000 |
* |
* |
0.023 |
0.8 |
0.3 |
Dittus e Boelter |
Fluido raffreddato |
|||
|
> 10000 |
* |
* |
0.027 |
0.8 |
0.33 |
Sieder e Tate |
Per prodotti Petroliferi |
|||
|
12000 – 220000 |
* |
* |
0.02(Di/De)0.53 |
0.8 |
0.33 |
Monrad e Pelton |
Aria o acqua sez. anulare sup. esterna isolata |
|||
Tabella 2 – Formule sperimentali per il calcolo del numero di Nusselt: convezione forzata.
|
Situazione geometrica |
Campo di validità (Ra) |
Nu=C.Grb.Prc |
Autori |
Note |
||
|
C |
B |
c |
||||
|
Superficie cilindrica orizzontale |
< 10-5 |
0.4 |
0 |
0 |
McAdams |
Nu e Gr cacolati in funzione del diametro D |
|
103 - 109 |
0.53 |
0.25 |
0.25 |
|||
|
109 - 1012 |
0.13 |
0.33 |
0.33 |
|||
|
Superficie piana o cilindrica verticale |
103 - 109 |
0.59 |
0.25 |
0.25 |
McAdams |
Nu e Gr calcolati in funzione della estensione verticale L |
|
109 - 1012 |
0.13 |
0.33 |
0.33 |
|||
|
Superficie piana orizzontale |
105 – 2.107 |
0.54 |
0.25 |
0.25 |
Fishenden e Saunders |
Flusso di calore verso l’alto |
|
2.107 – 3.1010 |
0.14 |
0.33 |
0.33 |
|||
|
Superficie piana orizzontale quadrata di lato L |
105 – 2.107 |
0.25 |
0.25 |
0.25 |
Flusso di calore verso il basso |
|
|
Sfera |
103 - 107 |
0.49 |
0.25 |
0.25 |
Bromham e Mayhew |
|
|
Strato verticale di altezza H e spes-sore L: una parete verticale più calda dell’altra |
< 2000 Pr |
1 |
0 |
0 |
Jakob |
Nu e Gr calcolati in funzione di L. Relazioni valide per l’aria |
|
(2.104 – 2.105) Pr |
0.18(H/L)-1/9 |
0.25 |
0 |
|||
|
(2.102 – 11.106) Pr |
0.065(H/L)-1/9 |
0.33 |
0 |
|||
|
< 103 |
1 |
0 |
0 |
Emery e Chu |
Nu e Gr calcolati in funzione di L. Relazioni valide per i liquidi, con 3 < Pr < 30000 |
|
|
103 - 107 |
0.28(H/L)-1/4 |
0.25 |
0.25 |
|||
Tabella 3- Formule sperimentali per il calcolo di Nusselt: convezione forzata.
|
Situazione geometrica |
Campo di Validità |
Nu = C.Rea.Grb.Prc |
Autori |
Note |
|||
|
C |
a |
b |
c |
||||
|
Condotto verticale con sezione circolare L/D=20 |
Re > 1600 |
0.525 |
0 |
0.25 |
0.25 |
Watzinger e Johnson |
Acqua che scende Raffreddandosi |
|
1600<Re<4600 |
0.255 |
0.07 |
0.25 |
0.37 |
|||
|
Condotto verticale con sezione circolare L/D=50 |
103 < Re < 105 |
0.032. .(D/X)0.05 |
0.8 |
0 |
0.37 |
Kirschbaum |
Re deve essere Modificato con l’aggiunta di un termine correttivo |
Tabella 4- Formule sperimentali per il calcolo del numero di Nusselt: convezione mista.