PROPAGAZIONE ESTERNA
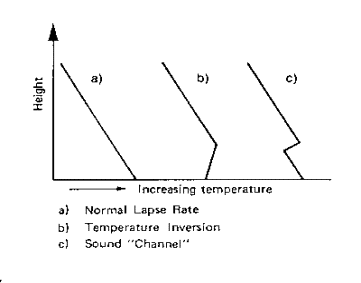
Figura 1-Grafico dell'altezza in funzione della temperatura
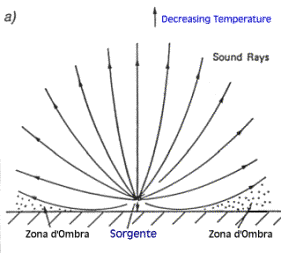
Figura 2- Andamento dei raggi sonori in condizioni normali
Caso a): In condizioni normali il raggio sonoro è incurvato
verso l’alto;data una certa altezza della sorgente da terra,esiste un raggio
limite che va a toccare il terreno,per cui al di sotto di esso si crea una zona
d’ombra,cioè una zona in cui al suono non arriva.
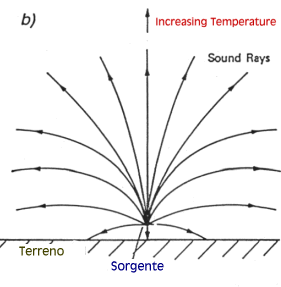
Figura 3
-Andamento dei raggi sonori in condizioni di inversione termica
Caso b): Se si verificano situazioni d’inversione termica,la situazione si rovescia rispetto al caso a):per cui i raggi sonori sono incurvati verso il basso,non si creano più zone d’ombra e quindi il rumore può oltrepassare eventuali ostacoli.Questa situazione d’inversione termica è piuttosto comune nella Pianura Padana,in cui circa il 30% del tempo in un anno è in questa condizioni climatiche.
Caso c):Questo fenomeno avviene normalmente in presenza di nebbia.Il terreno è caldo,ma la nebbia è più fredda e la temperatura scende.Appena si supera la coltre,il sole riscalda l’aria e la temperatura aumenta,fino a quando torna a prevalere la diminuzione di temperatura con l’altezza.Il suono viene intrappolato in un canale e può essere trasportato per parecchi chilometri ,prima di ricadere sul terreno,con un’attenuazione molto bassa.
Effetto della velocità del vento
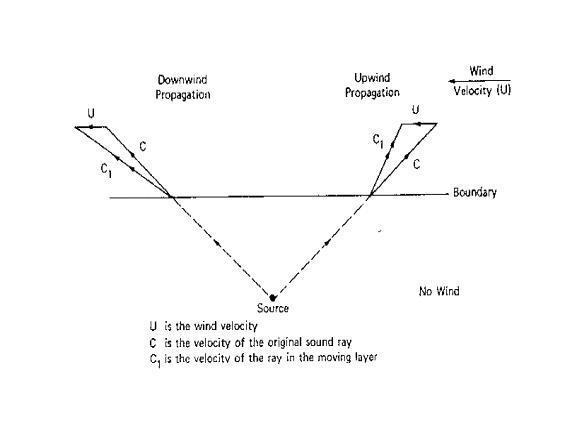
Figura 4- Propagazione del suono in funzione del vento
Quando ho il campo velocità ,il vettore di velocità del vento si somma vettorialmente col vettore velocità dello strato (c1).Se un raggio sonoro passa da una zona senza vento ad una zona con vento,la velocità del suono si somma alla velocità del medesimo.
La presenza di un gradiente di vento mi giustifica la curvatura dei raggi sonori;cioè non è l’intervento del vento in sé,ma il fatto che esso per ipotesi dell’aderenza fornisce sempre una velocità nulla a contatto col terreno ,mentre va aumentando con il crescere dell’altezza. I raggi sonori non sono curvati dal vento che scorre con una stessa velocità da terra. Infatti,se il vento è uniforme, non si ha un effetto di curvatura,ma semplicemente l’effetto della composizione vettoriale. Viceversa,in presenza di velocità anche ridotta ma con forte gradiente, si verifica la curvatura dei raggi sonori.Questa curvatura fa sì che si formino delle zone d’ombra,al di sotto dell’ultimo raggio tangente con il suolo.
A monte del vento della sorgente, il gradiente con la foga del vento curva i raggi verso l’alto. Se la velocità del vento varia linearmente con la quota,i raggi sonori curvano sottovento. A favore di vento si sentono di più i suoni, perché la curvatura dei raggi fa sì che il suono superi gli ostacoli.
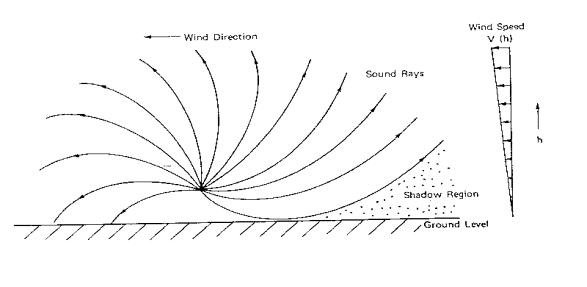
Figura 5-Propagazione del suono in relazione al vento
Esistono delle regole di calcolo di questi fenomeni? Bisognerebbe rispondere di no .In realtà esistono,in quanto c’è un regolamento ,che si chiama ISO 9313 – 2 ,il quale descrive le regole di calcolo di questi fenomeni causati dal vento.Di fatto,però,non le usa praticamente nessuno a causa della difficoltà dei calcoli.
Quindi,quando c’è vento mi metto in una situazione di controvento,quando ci sono dei gradienti termici mi metto in una situazione di inversione termica.Per cui considero sempre i raggi sonori presenti nell’aria con un certo raggio di curvatura.Questo raggio di curvatura viene descritto dalla norma.
Consideriamo ad esempio un raggio di curvatura di 3000 metri e supponiamo di voler calcolare la propagazione a 30 metri di distanza. L’arco è 1/100 del raggio,quindi è piuttosto trascurabile.Dunque la differenza tra la propagazione per raggio curvo e la propagazione per raggio dritto ,si apprezza quando la distanza di propagazione è confrontabile con il raggio di curvatura. A 500-600 metri il raggio di curvatura inizia già ad essere rilevante,ma non a 50-100 metri di distanza dalla sorgente.Noi consideriamo i raggi acustici per praticità sempre verso il basso.
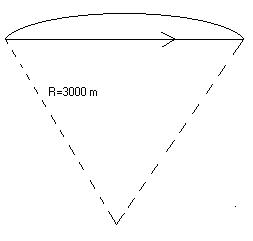
Figura 6-Raggio acustico incurvato verso il basso
Riflessione sul terreno

Figura 7-
Riflessione sul terreno
In generale si ha riflessione ogni volta che si ha una discontinuità e una interfaccia nel mezzo in cui un’onda sonora si propaga. L’onda riflessa dipende dall’onda incidente,dall’angolo di incidenza,dalla superficie riflettente e dalle impedenze caratteristiche dei mezzi.
Quando i raggi sonori provenienti da una sorgente incidono su una superficie piana,si formano dei raggi riflessi che sembrano provenire da una sorgente immagine,che si ottiene specularizzando la sorgente reale rispetto al campo.Come calcolare allora il livello sonoro?Esso sarà la somma del livello diretto più quello riflesso.Facciamo un esempio numerico.
Esempio:
La sorgente è situata ad un’altezza dal suolo ![]() = 4 m.Il ricevitore è
situato ad un’altezza
= 4 m.Il ricevitore è
situato ad un’altezza ![]() = 1.5 m.La distanza
tra la sorgente e il ricevitore e’ d = 25 m.Il livello della sorgente è 100 dB.
Infine,la superficie del terreno è caratterizzata da un valore di coefficiente
di riflessione
= 1.5 m.La distanza
tra la sorgente e il ricevitore e’ d = 25 m.Il livello della sorgente è 100 dB.
Infine,la superficie del terreno è caratterizzata da un valore di coefficiente
di riflessione ![]() = 0.1.Si vuole
calcolare il livello di intensità al ricevitore.Il livello riflesso è come se
provenisse da una sorgente virtuale,cioè la sorgente immagine
= 0.1.Si vuole
calcolare il livello di intensità al ricevitore.Il livello riflesso è come se
provenisse da una sorgente virtuale,cioè la sorgente immagine ![]() ,situata ad una quota
,situata ad una quota
![]() = -4 m.
= -4 m.
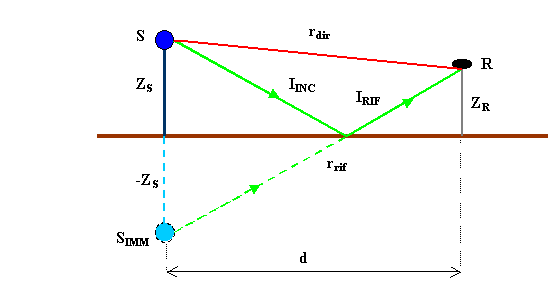
Figura 8-Suono riflesso su un terreno
![]()
Innanzitutto,calcoliamo il livello diretto. Siccome la sorgente è puntiforme, abbiamo:
![]() =
= ![]() - 11 – 20 log
- 11 – 20 log ![]() (1)
(1)
In realtà ![]() non è veramente 25
m,ma per essere precisi è:
non è veramente 25
m,ma per essere precisi è:
![]() =
=![]()
![]() = 25.12 m
= 25.12 m
Quindi,sostituendo nella (1) trovo:
![]() = 100 – 11 –
20 log (25.12) = 61 dB
= 100 – 11 –
20 log (25.12) = 61 dB
A questo punto calcoliamo il livello riflesso,che proviene da una
sorgente ![]() più lontana.
più lontana.
![]() =
= ![]() = 25.6 m
= 25.6 m
Per cui,sapendo che solo il 90% dell’energia passa,posso scrivere:
![]() =
= ![]() + 10 log (1-
+ 10 log (1-![]() ) – 11 – 20 log
) – 11 – 20 log ![]() = 60.38 dB
= 60.38 dB
A questo punto devo valutare come il suono riflesso si combina con quello diretto.Il suono calcolato in queste due quote impiega tempi diversi ad arrivare alla velocità di propagazione del suono c = 340 m/s.
![]() = 73.88 ms
= 73.88 ms
![]() = 75.29 ms
= 75.29 ms
Quindi, ![]() =1.41 ms .
=1.41 ms .
A noi interessa la variazione perché la natura del suono emesso da una sorgente è caratterizzata in termini di variabilità temporale della sua funzione di autocorrelazione.La funzione di autocorrelazione (ACF),è una funzione che mi indica quanto il segnale della sorgente rimane uguale nel tempo,confrontandolo con sé stesso traslato di un certo tempo.
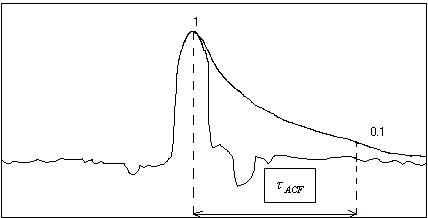
Figura 9-Funzione di autocorrelazione
La funzione di autocorrelazione ACF raggiunge il valore 1 per ![]() = 0 e va praticamente a 0 trascorso un tempo abbastanza
ridotto.Si definisce la durata effettiva della funzione di autocorrelazione
= 0 e va praticamente a 0 trascorso un tempo abbastanza
ridotto.Si definisce la durata effettiva della funzione di autocorrelazione ![]() ,quel valore per cui l’inviluppo della funzione di
autocorrelazione assume il valore 0.1 (cioè il 10%).Si può ritenere che quando
il segnale tende a mescolarsi con sè stesso con un
,quel valore per cui l’inviluppo della funzione di
autocorrelazione assume il valore 0.1 (cioè il 10%).Si può ritenere che quando
il segnale tende a mescolarsi con sè stesso con un ![]() >
> ![]() ,trovo un segnale che
non è assolutamente equivalente con sé stesso: abbiamo cioè due segnali
diversi.Quindi :
,trovo un segnale che
non è assolutamente equivalente con sé stesso: abbiamo cioè due segnali
diversi.Quindi :
se ![]() <
< ![]()
![]() la sorgente è incoerente.Si
sommano le due sorgenti non correlate e quindi con la normale somma energetica:
la sorgente è incoerente.Si
sommano le due sorgenti non correlate e quindi con la normale somma energetica:
![]() = 63.71 dB
= 63.71 dB
In questo caso il suono riflesso si è andato a mescolare con il suono diretto.
Se ![]() >>
>> ![]()
![]() la sorgente è coerente.
Vuol dire che il suono diretto e il suono riflesso interferiscono e a seconda
dalle fase si avrà:
la sorgente è coerente.
Vuol dire che il suono diretto e il suono riflesso interferiscono e a seconda
dalle fase si avrà:
- interferenza costruttiva
- interferenza distruttiva.
Per cui quando sono nel caso di interferenza costruttiva ho :
![]()
![]() = 66.71 dB
= 66.71 dB
Dove l’interferenza è distruttiva ho :
![]() = 37.76 dB
= 37.76 dB
Schermatura o diffrazione del suono
Quando le onde sonore incontrano un ostacolo,esse aggirano i bordi dell’ostacolo stesso dando luogo alla diffrazione del suono.In altre parole,le direzioni di propagazione delle onde sonore sono deformate dagli ostacoli che esse incontrano sul loro cammino.Inoltre le onde sonore sono diffratte più che riflesse se la loro lunghezza d’onda è paragonabile con le dimensioni degli oggetti che dovrebbero rifletterle.
Le onde sonore interagiscono con la materia,ma il loro comportamento è diverso se sono a basse oppure ad alte frequenze.

Figura 10-Diffrazione di uno schermo (a) e di un buco (b) a basse frequenze
La figura 10 illustra quello che succede alle basse frequenze attraverso un muro e attraverso un buco di parete.Mentre alle alte frequenze,nel caso dello schermo,l’onda cilindrica non è completa e si forma una zona d’ombra;nel caso del buco di una parete ho zone d’ombra sopra e sotto la fessura e poi si ha una parziale ricomposizione dell’onda nella zona successiva allo schermo.
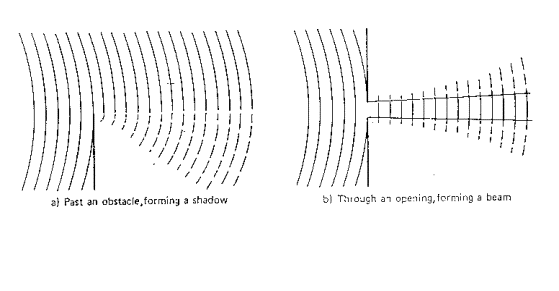
Figura 11-Diffrazione di uno schermo (a) e di un buco (b) ad alte frequenze
Supponiamo di avere una sorgente ,uno schermo (teoricamente indefinito) e un ricevitore dietro allo schermo in una posizione che non vede direttamente la sorgente.Gli studi più importanti sull’argomento sono stati fatti da Maekawa. I suoi risultati permettono di calcolare l’attenuazione :
![]() (*)
(*)

Figura 12-Differenza di cammino a causa di una barriera sottile
Nella figura
sono rappresentati i cammini che il suono percorrerebbe nel caso ci fosse lo
schermo(tratto verde) e nel caso in cui non ci fosse(tatto rosso).Abbiamo
quindi una differenza di cammino ![]() = A + B – d.
= A + B – d.
Si definisce
inoltre numero di Fresnel : N =![]() ,dove
,dove![]() è la lunghezza d’onda.Abbiamo che l’attenuazione in funzione
del numero di Fresnel, preso in scala logaritmica, è una funzione perfettamente
lineare.
è la lunghezza d’onda.Abbiamo che l’attenuazione in funzione
del numero di Fresnel, preso in scala logaritmica, è una funzione perfettamente
lineare.
La formula di Maekawa a seconda del tipo di sorgente è’:
-se la
sorgente è puntiforme ![]() = 10 log [3 + 20N]
= 10 log [3 + 20N]
-se la
sorgente è lineare ![]() = 10 log [2 + 5.5N]
= 10 log [2 + 5.5N]
Con il modello di Maekawa è possibile calcolare il valore dell’attenuazione.
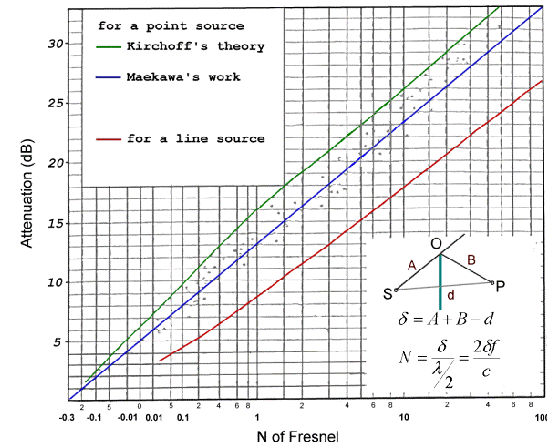
Figura 13-Diagramma di Maekawa
Esempio: Data una sorgente puntiforme calcolare il
livello sonoro dello schermo,sapendo che ![]() =100 dB,la frequenza dominante f è 250 Hz,d = 18 m,e
l’altezza h=3 m.Inoltre supponiamo di mettere lo schermo ad una distanza di 5 m
dalla sorgente.Di conseguenza la distanza del ricevitore dallo schermo è 13 m.
=100 dB,la frequenza dominante f è 250 Hz,d = 18 m,e
l’altezza h=3 m.Inoltre supponiamo di mettere lo schermo ad una distanza di 5 m
dalla sorgente.Di conseguenza la distanza del ricevitore dallo schermo è 13 m.
Vado a calcolare il cammino diffratto. Allora :
A = ![]() = 5.83 m B =
= 5.83 m B = ![]() = 13.34 m
= 13.34 m
Per cui ![]() =A + B – d = 1.271 m.
=A + B – d = 1.271 m.
Calcolo la
lunghezza d’onda: ![]() = 1.36 m.
= 1.36 m.
E quindi
adesso posso trovare il numero di Fresnel :
N = ![]() = 1.869.
= 1.869.
Applicando la prima formula di Maekawa cioè quella per una sorgente puntiforme trovo :
![]() = 10 log [3 + 20N]
= 10 log [3 + 20
= 10 log [3 + 20N]
= 10 log [3 + 20 ![]() 1.869] = 16 dB.
1.869] = 16 dB.
Quindi,se la sorgente aveva un livello di potenza di 100 dB,allora il livello diretto senza schermo era:
![]() =
= ![]() - 11 – 20 log d = 100 - 11 – 20 log 18 = 63.9
dB
- 11 – 20 log d = 100 - 11 – 20 log 18 = 63.9
dB
Applicando (*) trovo il livello schermato: ![]() = 47.9 dB.
= 47.9 dB.
Studio delle sorgenti sonore la cui emissione non è costante nel tempo
Ci sono molti casi in cui il livello sonoro non è costante nel tempo.Un primo approccio di studio di questo fenomeno consiste nell’analizzare l’effettiva legge di variazione del livello sonoro nel tempo.
Ad esempio possiamo considerare una sorgente che si attacca e si stacca ripetutamente.

Figura 14-Emissione di una sorgente non costante nel tempo
Come si fa a calcolare la rumorosità di questo esempio? Secondo l’approccio che abbiamo usato,potrei fare ad esempio 8 misure al secondo,cioè ogni 125 ms,ed andare ad osservare come si evolve il disegno nel tempo.Però non so quanto quale il rumore di fondo. E poi,ho superato il limite di legge?Infatti esistono dei limiti sul rumore esterno e sul rumore in ambiente di lavoro.Questi limiti vengono sempre espressi col concetto di livello equivalente.
Per livello equivalente,si intende il livello integrato su un tempo di misura.Ricordiamo la definizione di pressione media efficace:
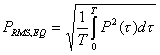
Il livello equivalente è definito :
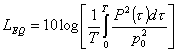 = 10 log
= 10 log 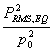
![]()
dove ![]() è la pressione
quadratica e
è la pressione
quadratica e ![]() è la pressione di
riferimento. Il
è la pressione di
riferimento. Il ![]() misura sempre da
0,cioè dall’istante in cui incominciamo la misura, al tempo T attuale.
Quindi,io posso continuare a calcolarlo mano a mano che passa il tempo:ciò
corrisponde alla linea blu della figura 14.
misura sempre da
0,cioè dall’istante in cui incominciamo la misura, al tempo T attuale.
Quindi,io posso continuare a calcolarlo mano a mano che passa il tempo:ciò
corrisponde alla linea blu della figura 14.
Nella figura
14,all’inizio il ![]() era basso perché
l’emissione della sorgente era basso. Poi,comincia a crescere (e quindi anche
il
era basso perché
l’emissione della sorgente era basso. Poi,comincia a crescere (e quindi anche
il ![]() ) ,poi cala e ricresce ancora periodicamente.Le oscillazioni
del livello equivalente tendono ad attenuarsi,per cui basta effettuare una
misura per un tempo sufficientemente lungo ,per fare in modo che il
) ,poi cala e ricresce ancora periodicamente.Le oscillazioni
del livello equivalente tendono ad attenuarsi,per cui basta effettuare una
misura per un tempo sufficientemente lungo ,per fare in modo che il ![]() risulti univocamente
stabile.
risulti univocamente
stabile.
La legge italiana parla di livello equivalente di lungo periodo che può essere: 8 ore per l’ambiente di lavoro (tipica giornata lavorativa), mentre in ambiente esterno distinguiamo il periodo diurno (dalle 6 alle 22) e il periodo notturno (dalle 22 alle 6).
Esempio : Il livello equivalente del suono di una sirena in una fabbrica è come segue dalla figura.Si ha una zona di rumorosità durante il giorno intorno ai 50 dB e per 30 secondi va a 80 dB. Calcolare il livello equivalente complessivo.

Figura 15-Suono della sirena in una fabbrica
Il numero di secondi in 16 ore
è: 16 ![]() 3600 = 57600 s , di
cui : 57570 a 50 dB e 30 a 80 dB. Quindi:
3600 = 57600 s , di
cui : 57570 a 50 dB e 30 a 80 dB. Quindi:
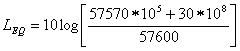 = 51.82 dB
= 51.82 dB
Dunque il livello equivalente è cresciuto molto poco.Supponiamo ora di avere 30 minuti ad 80 dB. Per cui ho 55800 s a 50 dB e 1800 s a 80 dB. Quindi:
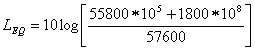 = 65.08 dB
= 65.08 dB
Esempio : Un operaio lavora 8 ore suddivise come suggerisce la tabella.Calcolare il livello equivalente.
|
ore |
macchina |
|
|
2 |
tornio |
82 |
|
1 |
fresa |
85 |
|
1 |
trapano |
78 |
|
0.5 |
smerigliatrice |
96 |
|
0.5 |
pausa |
65 |
|
3 |
saldare |
81 |
Abbiamo che :
 =
=
= 85.8 dB
La legge dice
di valutare il livello di esposizione personale ![]() ,che coincide con il livello equivalente
,che coincide con il livello equivalente ![]() nel momento in cui
l’operaio lavora 8 ore.Se però l’operaio lavora 10 ore,il
nel momento in cui
l’operaio lavora 8 ore.Se però l’operaio lavora 10 ore,il ![]() assume sempre 8 come
numero totale di ore.
assume sempre 8 come
numero totale di ore.
Esempio : Un operaio lavora 10 ore suddivise come suggerisce la tabella.Confrontare il livello di esposizione personale con il livello equivalente.
|
ore |
macchina |
dB |
|
2 |
Tornio |
82 |
|
3 |
Fresa |
85 |
|
1 |
Trapano |
78 |
|
0.5 |
Smerigliatrice |
96 |
|
0.5 |
Pausa |
65 |
|
3 |
Saldare |
81 |
 =
=
= 10 log ![]() = 85.68 dB
= 85.68 dB
![]() = 86.65 dB
= 86.65 dB
Per la legge devo considerare ![]() che risulta essere
più alto del livello equivalente.
che risulta essere
più alto del livello equivalente.
Il territorio viene suddiviso dal comune in 6 classi e in ciascuna di esse c’è un limite diurno e un limite notturno.
|
Classi |
Limite diurno/notturno |
Zona |
|
I.
|
50/40 |
Parchi pubblici ,ospedali,scuole,… |
|
II.
|
55/45 |
Quartiere residenziale |
|
III.
|
60/50 |
Mista,escluse le città(es. Pianura Padana) |
|
IV.
|
65/55 |
Centri storici,dove ci sono i negozi |
|
V.
|
70/60 |
Industriale normale |
|
VI.
|
80/70 |
Industriale |