Introduzione
I fenomeni acustici sono,
come è noto, fenomeni oscillatori che si propagano in un mezzo elastico. E’
evidente che una descrizione adeguata dei fenomeni sonori richiede la
conoscenza dei valori che in ogni istante assumono le grandezze acustiche, e in
particolare la pressione acustica, nei vari punti del mezzo interessato, ossia
la conoscenza particolareggiata del campo sonoro. Lo scopo principale di questa
lezione sarà appunto quello di esprimere le grandezze acustiche attraverso un
modello matematico; ci occuperemo quindi dello studio dell’equazione di
D’Alembert, di una sua applicazione e della sua soluzione analitica nel caso
specifico delle onde piane progressive. Infine introdurremo una nuova
grandezza, la densità dell’energia sonora.
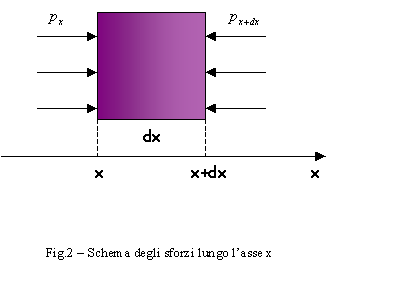
L’equazione di D’Alembert
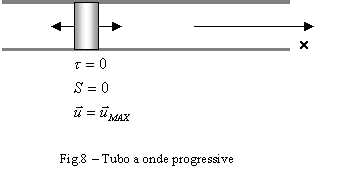
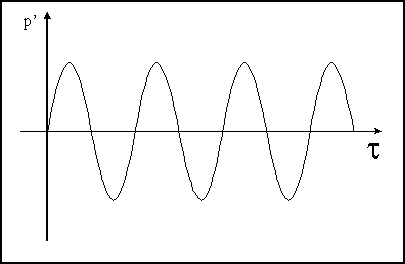
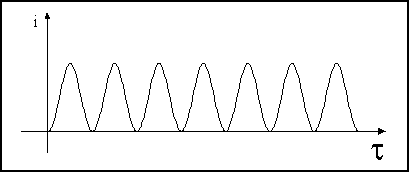
Fig. 9,10,11 - andamento
dell’intensità sonora istantanea nel caso in cui pressione e velocità siano
segnali sinusoidali in fase.
Facendo una media temporale dell’intensità
istantanea ricavo l’intensità media:
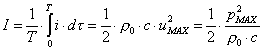
![]()
Visto che lavoriamo con segnali
sinusoidali possiamo sostituire i valori massimi con i rispettivi valori
quadratici medi (RMS – root mean squared): ![]() e
e ![]() e ricalcolare
l’intensità media:
e ricalcolare
l’intensità media:
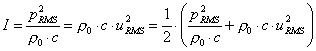
Densità dell’energia sonora
La densità di energia sonora D (o più brevemente, densità energetica) è definita
come l’energia sonora che, in un dato istante, risulta localizzata nell’unità
di volume circostante un punto assegnato del mezzo di propagazione; essa è cioè
la densità di distribuzione di energia sonora nel mezzo:
![]()
![]()
Riprendendo il caso dell’ onda
piana progressiva, detta A la sezione del cilindro, abbiamo
che:
![]() e
e ![]()
Per ![]() la densità sarà uguale a:
la densità sarà uguale a:
![]()
Ora riprendiamo la formula
dell’intensità media calcolata in precedenza:
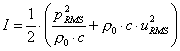
e andiamo a sostituirla nella relazione appena
calcolata; otteniamo così la densità dell’energia sonora per l’onda piana
progressiva:
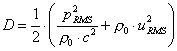
Osserviamo che l’equazione ![]() , dove U è la velocità dell’energia, nel
caso specifico dell’onda piana progressiva si riconduce a:
, dove U è la velocità dell’energia, nel
caso specifico dell’onda piana progressiva si riconduce a:
![]()
Quindi tra U e c vale la seguente relazione:
![]()
L’uguaglianza vale soltanto nel
caso delle onde piane progressive.
Da quanto è emerso in
questa lezione, nell’analisi di un campo sonoro dobbiamo determinare la
velocità e la pressione se vogliamo fare un’analisi fisica, mentre se vogliamo
fare un’analisi puramente energetica sono sufficienti i valori di intensità
sonora e di densità di energia.
Per descrivere i fenomeni
sonori, è consuetudine esprimere i valori delle grandezze acustiche attraverso
i livelli. Introduciamone alcuni:
·
Livello di pressione
![]()
· Livello di velocità
![]()
·
![]()
Livello di intensità
![]()
·
Livello di densità
![]()
Per un onda piana
progressiva tutti questi livelli sono uguali tra loro, in generale il livello
di intensità è più piccolo o al più uguale a quello di densità :
![]()
Definiamo come indice di reattività la differenza tra il livello di densità
e quello di intensità:
![]()
A volte però l’indice di reattività viene indicato come la differenza tra
il livello di pressione e il livello di intensità:
![]()
ma questo è sbagliato, perché questa differenza
potrebbe essere negativa; questo indicherebbe che un campo si può propagare più
velocemente di un’onda piana progressiva, e ciò è impossibile.