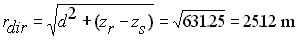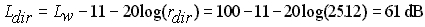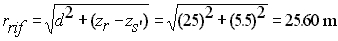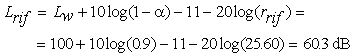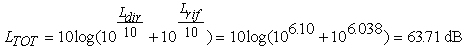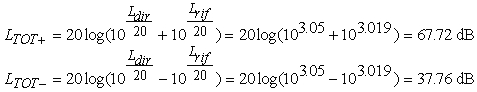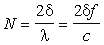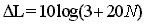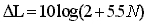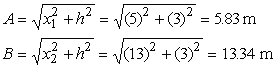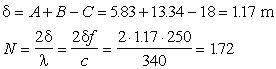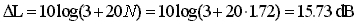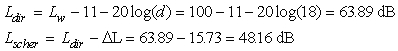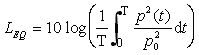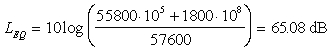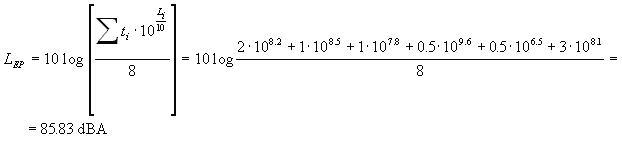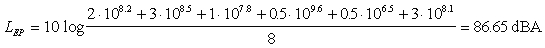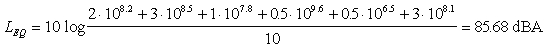PROPAGAZIONE IN AMBIENTE
ESTERNO
Durante questa lezione si sono studiati i fattori che influenzano la
propagazione delle onde sonore in ambiente esterno. Questi studi sono importanti
per capire in che modo possa variare la propagazione delle onde in particolari
condizioni in modo da poter progettare sistemi (come sistemi di amplificazione
per esterni) che funzionino correttamente in ogni situazione.
I fattori che
influenzano la propagazione del suono sono legati a fenomeni ambientali ma anche
alla presenza di barriere o superfici tra la sorgente ed il ricevitore.
Cercheremo ora di capire quali sono le variazione introdotte da tali fattori e
in che modo è possibile considerarle in fase di
progetto.
1. Effetto della
temperatura
Il primo fattore che influenza l’andamento dei fronti d’onda
è la variazione di temperatura. Infatti la temperatura varia al
variare della quota ed esistono diverse configurazioni di variazione.
Esamineremo ora tre casi che possono presentarsi:
a) Andamento
normale
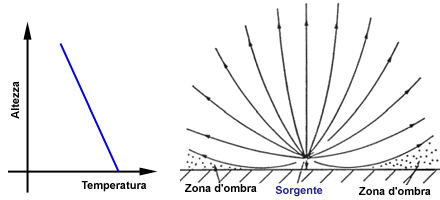
In condizioni normali la temperatura decresce man mano che ci si
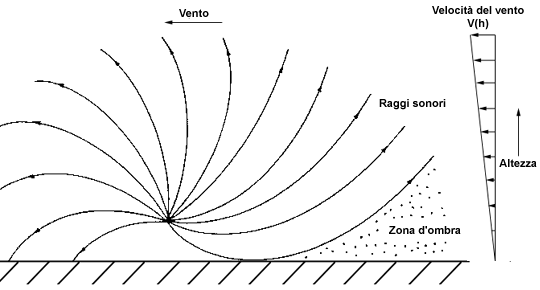
allontana dalla superficie. I raggi sonori (nelle varie figure rappresentati con
le linee di campo ortogonali al fronte d’onda e rappresentanti punti di
iso-intensità sonora) sono curvati verso l’alto. Esiste una
superficie limite teorica tangente al terreno, al di sotto della quale si forma
una zona d’ombra dovuta all’assenza di onde
sonore.
Figura 1: Andamento normale della temperatura e dei raggi
sonori
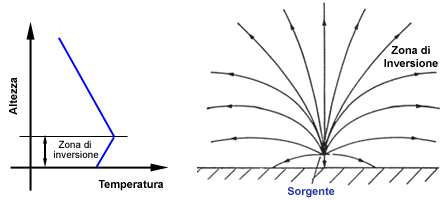
b) Inversione termica
In questa situazione il terreno è
più freddo dell’aria circostante e quindi a basse quote la
temperatura al suolo è più bassa della temperatura in quota.
All’aumentare della distanza dal suolo si ritorna ad un andamento di tipo
normale. Questa è una delle situazione climatiche tipiche di zone come la
pianura Padana. In questi casi i raggi sonori sono curvati verso
l’alto è ciò comporta
l’assenza di zone
d’ombra; questo può dare origine a strani fenomeni perché il
suono può “piovere” su zone che non sarebbero raggiungibili
se i fronti d’onda avessero l’andamento consueto.
Figura 2: Andamento della temperatura e dei raggi sonori
in caso di inversione termica
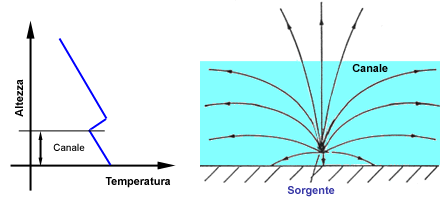
c) Canale sonoro
E’ il fenomeno più
“strano” e raro. Si forma un canale sonoro quando ho uno strato
d’aria che è più caldo (o più freddo) rispetto agli
strati circostanti. In questo caso le onde sonore vengono
“intrappolate” nello strato di diversa temperatura e possono uscire
soltanto quando varia nuovamente la temperatura; possono quindi percorrere anche
parecchi chilometri prima di ricadere e questo può dare origine ai
cosiddetti “miraggi sonori”. Una situazione simile si
può verificare in presenza di nebbia: infatti la coltre di nebbia sul
suolo forma una zona dove la temperatura e minore di quella del terreno, mentre
sopra lo strato di nebbia i raggi del sole rendono la temperatura più
alta. Questa variazione di temperatura crea un canale in cui possono restare
intrappolate le onde sonore
Figura 3: Andamento della temperatura e dei raggi sonori
in caso di canale sonoro
Nel progettare sistemi occorre tenere conto di questi fenomeni termici.
La normativa italiana stabilisce che in sede di calcolo è necessario
considerare il caso mediamente sfavorevole, cioè quello
dell’inversione termica.
2. Effetto del vento
Anche il vento può influire notevolmente sull’andamento
dei raggi sonori. In presenza di vento infatti la velocità del suono e
quella del vento si sommano come composizione vettoriale. In realtà,
il vento può trasportare il suono solo quando la velocità del
vento è confrontabile con quella del suono (e questo è abbastanza
raro).
Figura 4: Composizione vettoriale del vento con i raggi
sonori
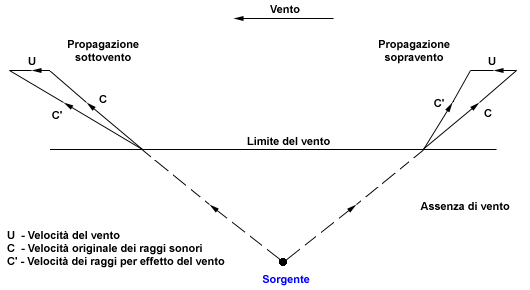
Il vento inoltre può curvare i raggi
sonori. Infatti in presenza di un gradiente di velocità al variare della
quota fa si che i raggi sonori curvino sottovento.
Figura 5: Effetto di curvatura del vento sui raggi
sonori
Questa curvatura data dal vento porta alla formazione di una zona
d’ombra sopravento e di una zona in cui il suono “piove”
sottovento.
Per tenere conto di questi fenomeni esiste la normativa
ISO-9613/2 che descrive i metodi di calcolo appropriati. Tale normativa risulta
però estremamente complessa, tanto da risultare praticamente
inapplicabile senza l’utilizzo di calcolatori avanzati.
Per
semplificare il calcolo considero sempre la condizione di sottovento e quindi
immagino i raggi sonoro sempre curvati verso il basso. In genere si utilizza un
raggio di curvatura di 2000 o 3000 metri. In ogni caso, la curvatura del raggio
sonoro si apprezza solo quando la distanza di propagazione è
confrontabile con il raggio di curvatura scelto.
3. Riflessioni sul
terreno
Il terreno è una fonte di riflessione per le onde sonore. Tale
riflessione dipende dalla superficie riflettente, dall’angolo che si forma
tra il suono e la superficie ed, in generale, dalla tipologia del mezzo in cui
avviene tale riflessione (infatti l’aria non è un mezzo
perfettamente elastico e può introdurre delle attenuazioni che dipendono
dall’umidità e dalla frequenza delle onde sonore).
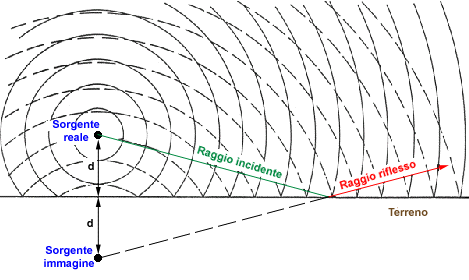
Per
calcolare l’entità di tale riflessione si utilizza
l’approssimazione della “sorgente immagine” che sfrutta
il fatto che i raggi riflessi sembrano provenire da una sorgente simmetrica a
quella reale rispetto alla superficie riflettente. Questa approssimazione
inoltre migliora tanto più la superficie considerata è liscia e
dura.
Figura 6: Riflessione su una superficie
piana
Per calcolare il livello in presenza di riflessione occorre quindi
considerare l’interazione di due sorgenti, una reale e una
“immagine” speculare a quella reale. Per prima cosa si calcola il
livello del suono diretto dovuto alla sorgente reale e poi si calcola il livello
dovuto alla riflessione. Nel fare questo occorre tenere presente che, come
detto, la riflessione dipende dalla superficie riflettente; infatti tale
superficie può non riflettere completamente il suono. Si definisce quindi
un coefficiente di riflessone α che esprime l’entità di
tale riflessione.
Una volta calcolati i due contributi occorre stabile in
che modo le due sorgenti interagiscono tra loro. Per fare ciò si
considera la funzione di autocorrelazione (ACF). Questa funzione indica
quanto il suono differisce da una sua replica ritardata. Questa funzione vale 1
in zero e decresce rapidamente raggiungendo un valore prossimo a zero dopo un
tempo abbastanza ridotto. Si
definisce quindi la durata effettiva
della funzione di autocorrelazione (τACF) come il tempo che
impiega l’inviluppo della funzione a raggiungere il valore 0.1
(cioè il 10% del valore massimo).
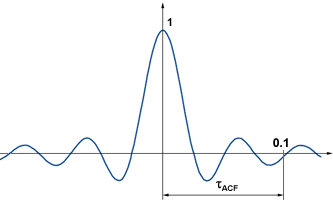
Figura 7: Un esempio di funzione di
autocorrelazione
Considerando il ritardo che intercorre tra il suono diretto e il suono
riflesso e la durata effettiva della funzione di autocorrelazione posso
stabilire in che modo interagiscono tra loro sorgente reale e sorgente immagine.
Infatti:
- Se τACF < Δt allora la sorgente è
incoerente e i due contributi si sommano usando la somma
energetica;
- Se τACF > Δt la sorgente è coerente e
suono riflesso e diretto interagisco tra loro. Tale interazione può
essere costruttiva (il livello totale aumenta) oppure distruttiva (il livello
totale diminuisce). In quest’ultimo caso si presenta un ulteriore problema
in quanto possono crearsi zone di cancellazione del
suono.
Vediamo di applicare il metodo descritto in un esempio
numerico:
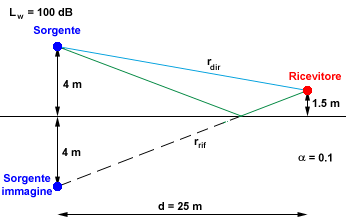
Esempio: Si consideri una sorgente puntiforme
posizionata a 4 m di altezza dal suolo ed un ricevitore posizionato a 1.5 m di
altezza ad una distanza di 25 m dalla sorgente. Sapendo che il livello della
sorgente è di 100 dB e che il terreno ha un coefficiente di riflessione
α = 0.1 si vuole calcolare il livello che raggiunge il
ricevitore.
Figura 8: Situazione dell'esempio
I livello che raggiunge il ricevitore è formato da due contributi:
quello diretto e quello dato dalla riflessione con il terreno. Partiamo
calcolando il primo. La distanza tra sorgente e ricevitore
è
Possiamo ora calcolare il livello diretto che essendo dato da una
sorgente puntiforme si calcola con la formula:
Ora dobbiamo calcolare il livello riflesso. Consideriamo quindi una
nuova sorgente immagine puntiforme ad una quota di -4 m. Prima di tutto
calcoliamo la distanza della nuova carica dal ricevitore:
Infine procediamo al calcolo del livello, tenendo conto che il terreno
ha un coefficiente di riflessione pari al
10%:
Per calcolare il livello totale occorre considerare in che modo suono
riflesso e suono diretto interagiscono. Calcoliamo per tanto i tempi di
propagazione ed il ritardo:
A seconda del valore di τACF otterremo valori diversi
di LTOT. Se τACF > Δt la sorgente
è incoerente e ottengo:
Se τACF < Δt posso avere interferenze
costruttive e distruttive. Indico con LTOT+ il livello dovuto
a interazione costruttiva e con LTOT- quello dovuto ad
interazione distruttiva:
ν
4. Diffrazione
Il fenomeno della diffrazione si verifica quando le onde sonore
oltrepassano il bordo di un ostacolo. Questo fenomeno porta ad una deformazione
delle onde ogni qual volta che si presenta un ostacolo durante la propagazione.
Inoltre si verifica una diffrazione quando le dimensioni di una superficie (su
cui teoricamente dovrebbe avvenire una riflessione) sono confrontabili con la
lunghezza d’onda del suono. La frequenza dell’onda sonora influisce
anche sul tipo di diffrazione che si verifica. Infatti ad alte frequenze si
verificano deformazioni completamente diverse da quelle che si osservano a bassa
frequenza. Ci si rende facilmente conto di questo se, ad esempio, si considera
la deformazione apportate da una fenditura in una parete:
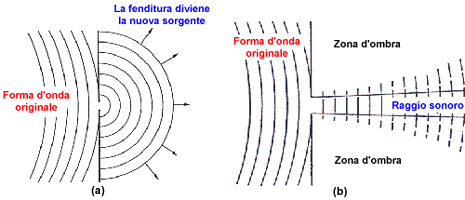
Figura 9: Diffrazione attraverso una fenditura a basse
frequenze (a) e ad alte frequenze (b)
Come illustra la figura, a basse frequenze la fenditura, per effetto
diffrattivo, diventa sorgente di un’onda sferica, mentre ad alte frequenze
dal foro si forma un raggio sonoro che è tanto più collimato tanto
più è alta la frequenza.
Un altro interessante caso di
diffrazione si ha quando si pone una barriera sottile lungo la propagazione
dell’onda. Anche qui si ottengono effetti diversi al variare della
frequenza dell’onda:
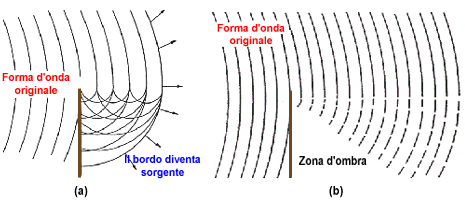
Figura 10: Diffrazione attraverso una barriera a basse
frequenze (a) e ad alte frequenze (b)
In questo caso ad altre frequenze si viene a creare una zona d’ombra
in prossimità della barriera (che potrebbe essere ad esempio un muro)
mentre lontano dall’ostacolo l’onda rimane praticamente
imperturbata.
Differente è l’effetto per le basse frequenze: in
questo caso infatti il bordo diviene a sua volta sorgente di un’onda
cilindrica e il livello sonoro che verrebbe avvertito da un ricevitore
posizionato oltre la barriera sarebbe dato dall’interazione
dell’onda diretta con l’onda rifratta.
In genere, è
difficile quantificare l’entità di questi fenomeni sia per basse
che per alte frequenze. Vi è però un’importante eccezione:
infatti è stata trovata un relazione analitica approssimata per
quantificare le variazioni introdotte da uno schermo sottile di lunghezza
indefinita posto tra sorgente e ricevitore. Tale approssimazione è nota
come relazione di Maekawa, dal nome dello studioso che la
presentò.
Immaginiamo di avere una sorgente puntiforme (o lineare) di
onde sonore, un ricevitore posto ad una certa distanza ed uno schermo
(teoricamente di lunghezza indefinita) posto tra sorgente e ricevitore in modo
da nascondere il ricevitore alla sorgete come illustrato in
figura:
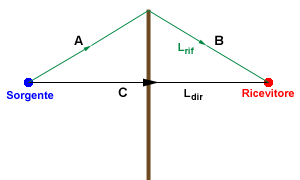
Figura 11: Diffrazione dovuta ad una barriera
sottile
La relazione di Maekawa ci consente di calcolare l’attenuazione
dovuta alla presenza della barriera. Tale attenuazione dipende dalla lunghezza
d’onda del suono e dalla differenza di cammino, cioè la differenza
tra il cammino teorico dell’onda diretta (indicato con la lettera C in
figura) e quello reale dell’onda diffratta (indicato con i tratti A e B in
figura). Generalmente la differenza di cammino si indica come δ = A + B -
C; si definisce inoltre il numero di Fresnel N come (tale valore è un
numero puro):
Nelle relazioni proposte da Maekawa l’attenuazione dipende dal
solo numero di Fresnel e, se rappresentate in scala logaritmica la relazione
è perfettamente lineare. Tali relazioni sono:
a) In caso di
sorgenti puntiformi:
b) In caso di sorgenti lineare:
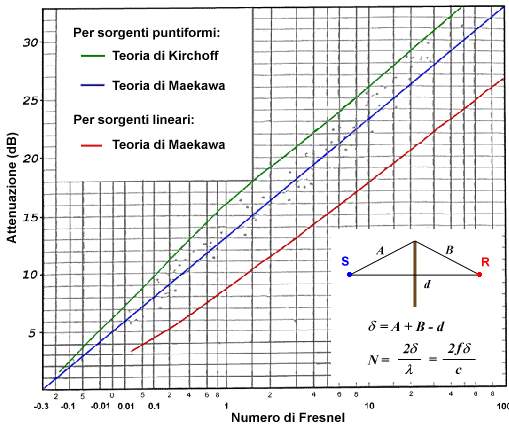
Nella grafico seguente vengono rappresentate le curve di Maekawa in
scala logaritmica. Viene inoltre rappresentata anche l’attenuazione
calcolabile con l’approssimazione di Kirchoff per sorgenti puntiformi.
Egli fu il primo a studiare il fenomeno diffrattivo cercando
un’approssimazione ma la sua teoria si rivelò errata
Figura 12: Diagramma di Maekawa
Vediamo ora un esempio applicativo di questa
teoria.
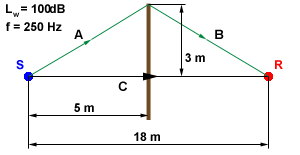
Esempio: Consideriamo un sorgente puntiforme di
livello sonoro
Lw = 100 dB con frequenza dominante
f =
250 Hz. Ad una distanza di 18 m dalla sorgente vi è un ricevitore. Fra
sorgente e ricevitore è presente una barriera sottile che sovrasta di 3 m
la sorgente e dista 5 m dalla sorgente stessa. Calcolare l’attenuazione
introdotta dalla barriera.
Figura 13: situazione dell'esempio
Per prima cosa occorre calcolare la differenza di cammino δ e
quindi il numero di Fresnel.
Indicando con x1 il tratto dalla
sorgente alla barriera e con x2 il tratto dalla barriera al
ricevitore dal teorema di Pitagora ricavo:
A questo punto possiamo facilmente calcolare δ e
N:
Ora calcoliamo l’attenuazione introdotta dalla barriera grazie
alla formula per sorgenti puntiformi di Maekawa:
Lo schermo posto tra sorgente e ricevitore introduce quindi
un’attenuazione di 15.73 dB su livello che si avrebbe senza ostacolo.
Calcoliamo ora quanto vale il livello percepito dal ricevitore:
ν
In queste considerazioni sulla diffrazione data da una barriera si
è sempre trascurato ogni altro contributo. Infatti, non si è mai
presa in considerazione il terreno che può introdurre una riflessione;
tenendo conto della riflessione occorre tenere presente che anche le onde
riflesse subiscono il fenomeno della diffrazione. E’ poi possibile
estendere il ragionamento della barriera in più dimensione considerando
un ostacolo formato da un piano in un sistema di riferimento in 3 dimensioni. In
tal caso ognuno dei bordi introduce una diffrazione.
5. Valutazione della rumorosità dei
suoni
Fino ad ora abbiamo considerato sorgenti sonore con un livello sonoro
costante nel tempo. In realtà, vi sono molti casi in cui il livello
sonoro non è costante nel tempo e occorre valutarne la rumorosità.
Un primo approccio a questo problema è quello di ricercare la funzione
matematica che descrive l’andamento del livello sonoro. Questo ci consente
di valutare il livello sonoro il un dato istante ma non fornisce
un’informazione sulla rumorosità globale. Se ad esempio avessimo
una sorgente che si accende ad intermittenza, conoscere esattamente
l’andamento del tempo non ci aiuta nel valutare il livello sonoro che
produce in un determinato tempo. Si definisce quindi un livello
equivalente che si calcola come:
Il livello equivalente rappresenta una sorta di media del livello
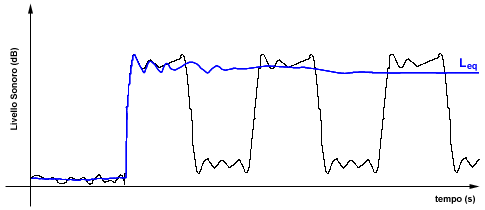
sonoro sul periodo di tempo T considerato. In figura è rappresentato
l’andamento (quantitativo) del livello emesso da una sorgente
intermittente ed il corrispondente livello
equivalente:
Figura 14: Livello sonoro di una sorgente intermittente e
livello equivalente
Come si vede dal grafico, il livello equivalente si stabilizza sempre
più all’aumentare della finestra di integrazione considerata.
L’importanza di questo livello è quella di consentirci di
quantificare il livello sonoro emesso da una sorgente attraverso un unico
numero. Infatti il livello equivalente è usato nella legislazione per
stabilire i limiti tollerabili di rumore. In particolare la legge italiana
stabilisce tre intervalli di tempo diversi per effettuare le
rilevazioni:
- 8 ore, che corrispondono al tempo di lavoro da utilizzare per misurare la
rumorosità sul luogo di lavoro;
- dalle 6 alle 22, corrispondenti al periodo diurno
- dalle 22 alle 6, corrispondenti al periodo notturno
Tutte
le misure che si effettuano durante il giorno vanno integrate sulle 16 ore del
periodo diurno e, similmente, le misure effettuate di notte vanno integrate
sulle 8 ore del periodo notturno. Vediamo ora un esempio delle modalità
di calcolo del livello equivalente.
Esempio: Si vuole
misurare il livello equivalente di una sirena che segnala la pausa pranzo in una
fabbrica. Questa sirena suona alle 12 precise e rimane in funzione per 30
secondi.
Teoricamente dovrei misurare il livello sonoro per 16 ore per
determinare l’andamento del livello sonoro nel periodo diurno. Questa
strada in realtà non è percorribile. Procedo allora misurando per
un’ora il livello sonoro a sirena spenta e poi i 30 secondi in cui suona
la sirena. Dalle misure effettuate risulta che:
- 50 dB per 1 h in cui la sirena era spenta
- 80 dB per i 30 s in cui la sirena era in
funzione
Estendiamo ora le nostre misure campione per tutto il
periodo diurno. Nel tempo totale tTOT = 16 h = 576000 s di
finestra legale, per t1 = 30 s abbiamo misurato un livello
sonoro di L1 = 80 dB, nel restante tempo t2 = 57570
s consideriamo valida la misurazione di L2 = 50 dB effettuata
per un’ora.
A questo punto l’integrale si trasforma in una somma
discreta ed è semplice calcolare il livello equivalente
come:
Si nota come la sirena influenzi molto poco il livello equivalente che
aumenta di meno di 2 dB rispetto al livello a sirena spenta. Supponendo invece
che la sirena suoni per 30 minuti (pari a 1800 s) invece che per 30 secondi,
ripetendo i calcoli otterrei:
ν
Il procedimento illustrato nell’esempio è valido per
qualunque misura effettuata in ambiente esterno. Nel caso in cui si debba misura
il livello sonoro a cui è esposto un lavoratore sul luogo di lavoro il
modo di procedere cambia leggermente
Infatti la legge italiana stabilisce che
in questi casi occorre considerare il livello di esposizione personale
(LEP). Questo livello si calcola analogamente, ma il calcolo è
sempre effettuato sulle 8 ore lavorative, indipendentemente dalle ore lavorate
dalla persona; solo nel caso in cui la persona considerata lavori per 8 ore il
livello equivalente e quello personale coincidono.
Vediamo questo discorso
applicato a due esempi pratici.
Esempio 1: Un lavoratore su
più macchine durante le 8 ore della giornata lavorativa. Calcolare il
livello di esposizione personale.
Tempo (h)
|
Macchina usata
|
Livello (dBA)
|
2
|
tornio
|
82
|
1
|
fresa
|
85
|
1
|
trapano
|
78
|
0.5
|
smerigliatrice
|
96
|
0.5
|
pausa pranzo
|
65
|
3
|
saldatrice
|
81
|
Il livello di esposizione personale in questo caso coincide con il
livello equivalente in quanto il lavoratore ha lavorato per 8 ore. Procediamo
nei calcoli come al solito e otteniamo:
ν
Esempio 2: Un lavoratore su più macchine per un totale
di 10 ore lavorative. Calcolare il livello di esposizione
personale.
Tempo (h)
|
Macchina usata
|
Livello (dBA)
|
2
|
Tornio
|
82
|
3
|
Fresa
|
85
|
1
|
Trapano
|
78
|
0.5
|
Smerigliatrice
|
96
|
0.5
|
Pausa
|
65
|
3
|
Saldare
|
81
|
In questo caso le ore lavorate sono 10, ma il livello personale va
comunque calcolato sulle 8 ore standard come segue:
Se effettuassimo il calcolo del livello equivalente (ovvero
dividessimo per 10 nella formula precedente otterremmo:
ν
6. Limiti di
rumore
La legge italiana stabilisce dei limiti di rumore per tutelare la salute
dei cittadini. Sia sul posto di lavoro che nell’ambiente esterno esistono
dei limiti che è obbligatorio rispettare se non si vuole incorrere in
pesanti sanzioni.
Sul posto di lavoro, come detto, il livello viene misurato
come livello di esposizione personale e la legge stabilisce 4 fasce di
rumorosità:
Sotto 80 dBA
|
il rumore è considerato tollerabile senza che il lavoratore subisca
danni permanenti;
|
Tra 80 dBA e 85 dBA
|
sono obbligatorie visite periodiche per i lavoratori e controlli costanti
sul rumore per tentare di ridurlo;
|
Tra 85 dBA e 90dBA
|
obbligo di intervento sui macchinari in quanto la legge proibisce
l’utilizzo di macchine che producono un livello di rumore superiore a 85
dBA. Inoltre sono obbligatorie visite ogni anno per i dipendenti;
|
Oltre 90 dBA
|
in questo caso è necessaria una denuncia entro 60 giorni alle
autorità competenti. In mancanza di una denuncia, la fabbrica può
incorrere nella chiusura e in una multa (intorno ai 30000.00 EUR) per ogni
giorno successivo al 60.
|
Tabella 1: Limiti di rumore nell'ambiente di
lavoro
In ambiente esterno invece esistono limiti diversi. La legge stabilisce 6
zone con limiti di rumore diversi per il periodo diurno e per quello notturno.
Le zone sono riassunte nella tabella seguente:
Zona
|
Limite diurno (dBA)
|
Limite notturno (dBA)
|
Nome zona
|
1°
|
50
|
40
|
Alta cautela (ospedali, scuole, ...)
|
2°
|
55
|
45
|
Residenziale
|
3°
|
60
|
50
|
Campagna
|
4°
|
65
|
55
|
Centri storici
|
5°
|
70
|
60
|
Industriale normale
|
6°
|
80
|
70
|
Esclusivamente industriale
|
Tabella 2: Limiti di rumore in ambiente
esterno