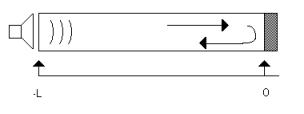
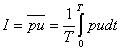ONDE STAZIONARIE
Prima di tutto dobbiamo affermare che questa proprietà non è specifica
delle onde acustiche, ma di tutte le onde in genere.
La formazione di onde
stazionarie è un caso d'interferenza (ovvero sovrapposizione), dato che si
tratta della somma di onde di uguale frequenza ma di fase non ovunque uguale.
In acustica per ottenere
la sovrapposizione di 2 onde di ugual
frequenza è relativamente semplice, basta considerare un’onda sonora e la
corrispondente onda riflessa da un qualsiasi materiale.
Se consideriamo il
precedente fenomeno isolato all’interno di un tubo troveremo punti chiamati Nodi
dove onde trasmesse e riflesse arrivano in opposizione di fase e, componendosi
annullano i loro effetti; mentre nei cosiddetti Ventri, esse arrivano in
concordanza di fase ottenendo massima
risultante dalla loro somma. Sulla formazione di onde stazionarie è
basato il funzionamento delle casse risonanti
o casse armoniche degli strumenti musicali.
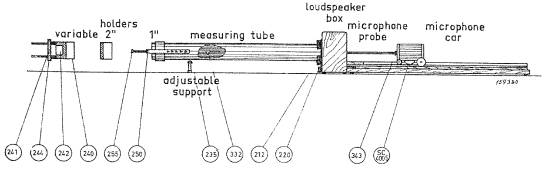 Figura 1
Figura 1
Questo fatto può essere
messo facilmente in evidenza mediante il tubo di Kundt (Figura 1), che è un
semplicissimo pezzo di tubo di vetro del diametro di un paio di cm, e della
lunghezza di circa 1 m, tagliato agli estremi e disposto orizzontalmente.
Un tappo di sughero forzato
nel tubo può esservi spostato mediante un lungo manico o bacchetta, delimitando
così la porzione di tubo utilizzata per l'esperimento. Sul fondo del tubo si
dispone una traccia di polverina costituita da granellini particolarmente fini
e leggeri. Si dispone una sorgente sonora all'estremità aperta del tubo.
Spostando il tappo di sughero nel tubo di vetro si ricerca lunghezza utile di
quest'ultimo per la quale la colonna
d'aria in esso contenuta entra in risonanza con la nota emessa dalla sorgente di
onde sonore.
Si nota allora che la
formazione di onde stazionarie nell'area contenuta nel tubo è visualizzata
dalla disposizione della polvere che, in corrispondenza dei ventri si sparge su
un'ampia porzione della parete del tubo mentre, in corrispondenza dei nodi giace sul fondo dello
stesso.La distanza tra ventri e nodi, così rilevata, consente una misura delle
lunghezze d'onda acustiche.
Nella realtà non esistono
materiali che consentono una riflessione totale dell’onda sonora (con impedenza
Z infinita), cioè questi ultimi
saranno responsabili di una attenuazione d’ampiezza dell’onda riflessa.
Studiando l’acustica,
diventa quindi indispensabile analizzare il comportamento dei materiali se
sottoposti a sollecitazioni sonore.
Coefficienti Acustici
Analizzando l’acustica
diventa indispensabile conoscere il comportamento dei materiali sottoposti a
sollecitazioni sonore.
Quando il treno d’onde
iniziale viene a contatto con un materiale con caratteristiche meccaniche
(principalmente impedenza) si suddivide
in 3 parti: una parte delle onde è riflessa dal materiale e torna indietro,
un’altra parte è assorbita dal materiale ed infine una parte attraversa il
materiale stesso. In termini di intensità sonora si riassume nella figura 2:
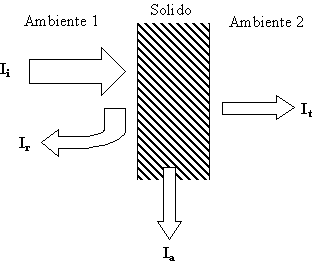
Figura 2
In termini di intensità
si definiscono tre indici:
·
Intensità Incidente
(Ii): l’intensità che ha
l’onda appena prima di entrare
in contatto con il materiale;
·
Intensità Assorbita
(Ia): l’intensità
della parte d’onda assorbita;
·
Intensità Trasmessa
(It): l’intensità
della parte d’onda trasmessa oltre il materiale;
·
Intensità Riflessa (Ir):
l’intensità della parte d’onda riflessa;
Esprimendo quanto disegnato
in formule analitiche:
![]() (1)
(1)
dividendo la precedente per
Ii si ha
![]()
dove si definiscono tre
nuovi valori:
·
Coefficiente
d’Assorbimento: ![]() = a
= a
·
Coefficiente di
Riflessione: ![]() = r
= r
·
Coefficiente di
Trasmissione: ![]() = t
= t
e la loro somma da 1; in
particolare si possono vedere così:
![]() (2)
(2)
Ora
possiamo individuare il Coefficiente di Assorbimento Acustico Apparente (a),
che è il principale strumento per valutare la capacità di assorbimento acustico
di un materiale; il suo valore è:
![]() (3)
(3)
Come si vede dalla
definizione di Coefficiente Apparente, per valutare la capacità di
assorbimento di un materiale non importa la quantità di suono assorbito o
trasmesso ad un ambiente esterno collegato, ma la quantità di onde riflesse; è
anche per questo che tale coefficiente è detto di assorbimento apparente, in
realtà infatti considera solo le onde riflesse e la condizione migliore si ha
quando tutto il suono è assorbito dal materiale.
Il caso migliore ed
ideale si ha quando r = 0 e quindi a = 1, in questo caso si parla di materiali perfettamente fonoassorbenti, nel
caso (a = 0 e r =
1) si parla invece di materiali perfettamente riflettenti.
Facendo un esempio
pratico, considerando la diffusione del suono in una stanza chiusa con una
finestra, il migliore materiale assorbente acusticamente sono le finestre
aperte; infatti l’aria è il materiale con minor coefficiente di riflessione
acustica essendo la sua densità e consistenza molto piccola (ovvero offrendo un
impedenza molto piccola).
Tralasciando il
paradosso della finestra che ha scarso significato ingegneristico, buoni
materiali che offrono alto assorbimento delle onde sonore sono i materiali
espansi a celle aperte come il poliuretano espanso, lana di roccia, velluto,
ecc. O in generale i materiali detti fonoassorbenti (con valori di a prossimi a 1). La caratteristica comune di questi materiali è che si
lasciano attraversare dall’aria opponendo però molta resistenza, il che
equivale a presentare un’alta impedenza per le onde sonore.
Il principio con
cui funzionano tali materiali fonoassorbenti è quello di incanalare le onde
sonore in tanti cunicoli di piccolissime dimensioni smorzando le stesse per
effetto del loro attrito contro le pareti di tali cunicoli. Inevitabilmente
questo attrito che viene prodotto si trasforma in calore e moto vibrazionale delle
pareti stesse.
Come
Calcolare il
Coeff.di
Assorbimento Apparente
Prendiamo un
altoparlante ed inseriamolo all’interno di un tubo, ed all’estremità opposta
mettiamo un materiale che ha la capacità
di riflettere (o meglio senza variazione di ampiezza o frequenza) quello che gli viene trasmesso . Se
l’altoparlante produce un tono puro avremo un treno d’onde che finendo contro
il tassello del precedente materiale ideale verrà riflesso. Tutto questo
provocherà punti (o meglio piani siccome il fronte d’onda prodotto
dall’altoparlante è piano) in cui l’onda diretta e quella riflessa avranno
interferenza costruttiva oppure
distruttiva.
·
L’impedenza del
campione che chiude il tubo è zloc=p/u
Per come è definito il
potenziale della velocità possiamo ricavare l’espressione della velocità u:
Possiamo ora scrivere il
potenziale della velocità delle particelle del mezzo (risulta particolarmente
semplice perché il caso è monodimensionale):
![]() (9)
(9)
dove f+ è il massimo potenziale dell’onda incidente f- è il massimo potenziale dell’onda riflessa; ed effettuando la derivata spaziale della
(12) ottengo:
![]() (10)
(10)
e la pressione p grazie alla relazione:
![]() (11)
(11)
dove ![]() indica la densità
media dell’aria prima della sollecitazione acustica dovuta altoparlante:
indica la densità
media dell’aria prima della sollecitazione acustica dovuta altoparlante:
![]() (12)
(12)
Per porre la condizione
al contorno devo calcolare l’impedenza z:
![]() (13)
(13)
![]() (14)
(14)
E’ possibile
riscrivere l’espressione della pressione in questo modo:
![]() (15)
(15)
dove
![]() e
e ![]() (16)
(16)
attraverso la
stessa semplificazione posso riscrivere
la velocità(10):
a questo punto possiamo
scrivere z utilizzando le (14),(16), (17):
![]() (18)
(18)
ricordando che ![]() (dove k è il numero d’onda).
(dove k è il numero d’onda).
Applicando la condizione
al contorno la (18) si può scrivere :
(19)
A questo punto definendo
il rapporto di riflessione CRF come:
![]() (20)
(20)
possiamo calcolare il
coefficiente d’assorbimento a
 o
anche
o
anche ![]() (21)
(21)
Utilizzando la (20) riscriviamo la (19):
![]() (22)
(22)
Dunque se dalla (22)si
calcola CRF:
![]() (23)
(23)
posso dare l’espressione
per calcolare a derivante dalla (21):
 (24)
(24)
Dopo tutti questi calcoli ci siamo accorti che saranno punti in cui la
pressione dovuta all’onda diretta e quella dovuta all’onda riflessa si sommano
ed altri in cui avviene un’interferenza di tipo distruttivo.
Analiticamente,questo si scrive:
![]()
![]() (25)
(25)
Vediamo ora quali sono i
passi da compiere per misurare sperimentalmente il valore del coefficiente di
assorbimento.
Operazioni sperimentali per
l’individuazione
del
Coeff.di Assorbimento
E’ semplice misurare i
valori di minimo e massimo della pressione all’interno del tubo, occorre un
microfono a pressione in grado di muoversi al suo interno.
In questo modo si misura
solo il modulo della pressione; per riuscire ad ottenere anche la fase
dell’onda occorre misurare la distanza d,
tra un massimo o un minimo della
pressione, e dove il tubo è chiuso, ed infine imponendo la relazione:
![]() (26)
(26)
Dove il –1 indica
che le due onde sono in controfase.
![]()
![]() (27)
(27)
![]() (28)
(28)
N.B. Tuttavia la fase dell’impedenza non ha un preciso significato fisico;
l’effetto dovuto a un materiale a impedenza complessa equivale a quello di un
materiale a impedenza reale spostato a destra o a sinistra rispetto alla
posizione in cui effettivamente si trova durante l’effettuazione della misura.
Il contributo della fase può essere interpretato come se l’onda riflessa non
fosse generata sulla superficie del campione ma a una certa “profondità”. Per
questa ragione, normalmente si richiede solo il modulo dell’impedenza.
Notiamo anche che pmin non è nullo in quanto
l’onda riflessa ha intensità minore di quella incidente.
Possiamo
ora sperimentalmente fare una lettura della pressione, attraverso un microfono
posto all’interno del tubo.
Osservando il grafico 1,
bisogna ricordarsi che il microfono non può distinguere l’onda incidente da
quella riflessa, e quindi P sarà la
somma delle due onde.
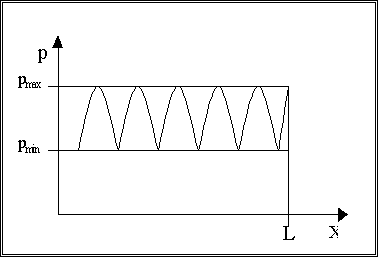
Grafico 1
Il metodo appena
descritto per individuare ![]() e di conseguenza il
valore dell’impedenza del materiale,presenta l’enorme svantaggio della
dispendiosità in termini di tempo. Infatti questo strumento richiede la
presenza di un operatore, che per ogni frequenza del suono dell’altoparlante
sposti il microfono lungo l’asse delle x alla ricerca del valore minimo della
pressione. Inoltre risulta difficile effettuare misure accurate soprattutto
alle alte frequenze dove le lunghezze d’onda sono molto piccole, ed un errore
di qualche
e di conseguenza il
valore dell’impedenza del materiale,presenta l’enorme svantaggio della
dispendiosità in termini di tempo. Infatti questo strumento richiede la
presenza di un operatore, che per ogni frequenza del suono dell’altoparlante
sposti il microfono lungo l’asse delle x alla ricerca del valore minimo della
pressione. Inoltre risulta difficile effettuare misure accurate soprattutto
alle alte frequenze dove le lunghezze d’onda sono molto piccole, ed un errore
di qualche ![]() m può diventare rilevante.
m può diventare rilevante.
Per ovviare a questo
problema si usano due microfoni fissi, distanti d, all’interno del tubo.Questi possono compiere le stesse
operazioni di prima senza spostare continuamente il microfono per trovare i
massimi e i minimi.
Dai due microfoni leggo
le due pressioni p1 e p2, e da esse posso
ricavare:
![]() (29)
(29)
![]() (30)
(30)
e da qui è possibile
calcolare il coefficiente di assorbimento del
materiale grazie alle formule(4)(5)(6).
Dove il primo addendo
della (32) rappresenta la Densità Cinetica (Dc) mentre il
secondo la Densità Potenziale (Dp).In assenza di eventi
esterni, per la legge della conservazione dell’energia queste due componenti si bilanceranno in modo che la loro somma
sia costante.
In generale il grado di
assorbimento varia in funzione della frequenza (f) e dello spessore del materiale (confrontando lo stesso materiale
a diversi spessori).
Graficamente:

Grafico 2
La capacità
fonoassorbente di un materiale quindi non è costante a tutte le frequenze e per
essere apprezzabile deve essere dell’ordine della lunghezza delle onde sonore
che deve smorzare. Inoltre ci sono comportamenti limite: alle basse frequenze
per ottenere alti valori di a è necessario usare materiali con grandi spessori o
meglio ricorrere ad altre tecniche di assorbimento acustico; al contrario alle
altissime frequenze bastano materiali semplici e di piccolo spessore.
Come si vede è difficile
individuare un corretto spessore in grado di comportarsi uniformemente a tutte
le frequenze; una regola che comunque è usata per stabilire quanto spesso deve
essere il materiale fonoassorbente è:
![]() (33)
(33)
(dove s lo spessore del materiale da usare e l la lunghezza d’onda del suono).
Per assorbire le basse
frequenze di solito si usano sistemi di doppie pareti una esterna cedevole al
suono e una interna rigida, separate da un sottile strato d’aria o di materiale
elastico.
L’effetto che si crea è
simile a quello di una massa M collegata
ad una molla fissata (di elasticità k)
ad una parete come in figura:

Figura 4
Questo sistema quando si
trova in condizioni di risonanza assorbe completamente le oscillazioni imposte
dalle onde sonore. Tale frequenza di oscillazione, detta frequenza naturale di oscillazione è:
![]() (34)
(34)
E’ comunque importante
notare la distinzione tra assorbimento acustico ed isolamento acustico: nel
primo caso si fa riferimento alla riflessione delle onde sonore, nel secondo
caso si parla di isolamento di un ambiente dalle onde acustiche di un altro
ambiente ad esso collegato.
Ad esempio sul soffitto
delle aule della nostra facoltà è stato utilizzato del polistirene ondulato, in
modo che le onde sonore della voce dell’insegnante scontrano con esso si infrangono disperdendosi in tante onde più
piccole con direzione casuale(oltre che ad essere convogliate nei pori
piccolissimi di questi materiali). Quindi nelle aule universitarie si predilige
il suono diretto rispetto a quello riflesso, che a volte risulta spiacevole
perché produce l’eco.
Propagazione
del suono in ambiente esterno
Gli esempi che si possono
fare su sistemi interessati da queste speculazioni sono molteplici:
·
rumore prodotto da
mezzi di trasporto (auto, treni, aeroplani)
·
edifici (sistemi di
refrigerazione, ventilatori)
·
sistema di
amplificazione per esterni (per concerti in uno Stadio)
Propagazione
Sferica
La propagazione
sferica è facile da descrivere: una distanza sorgente – ricevitore
sufficientemente elevata rispetto alla lunghezza d’onda in modo che quest’ultimo possa considerare
la sorgente come un punto.
L’energia che si propaga
resta in prima approssimazione costante (nessun assorbimento da parte
dell’aria) ma la intensità sonora diminuisce perché si distribuisce su una
superficie sempre più grande.
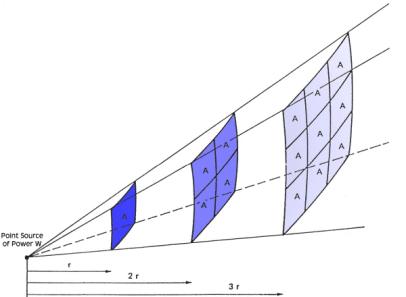
Figura 5
![]()
Sia LI1=80dB
l’intensità a 1m, LI2 a 2m vale ![]() . La diminuzione di intensità al raddoppio della distanza ha
una sigla (DL2) e nel caso della propagazione sferica vale sempre DL2=6dB ed è
il livello massimo che si può ottenere da una qualsiasi propagazione.
. La diminuzione di intensità al raddoppio della distanza ha
una sigla (DL2) e nel caso della propagazione sferica vale sempre DL2=6dB ed è
il livello massimo che si può ottenere da una qualsiasi propagazione.
|
|
|
|
|
|
|
|
|
Sono tutti livelli
espressi in decibel. Solo LW non è omogenea alle altre (il livello di potenza dipende dalla
sorgente e di conseguenza LW resta costante in ogni punto)
Fissato dunque LW, possiamo dedurre il livello di intensità: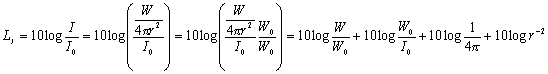
Essendo i valori di
riferimento W0 e I0 arbitrari li possiamo scegliere
uguali al fine di semplificare la relazione e i loro valori effettivi (valori
che saranno spiegati in seguito) sono:
 e dalle altre relazioni
e dalle altre relazioni
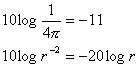
Possiamo ricavare la (36) dalla (35):
![]() (40)
(40)
Determinato questo valore
vogliamo che le altre relazioni (37)
(38) e (39) assumano in
un dato punto lo stesso valore che assume LI
per poter così parlare di unico Livello
Sonoro, e ciò è sempre possibile visto che i valori di riferimento sono
arbitrari.
Conosciamo anche una
relazione che unisce la velocità alla pressione (solamente nelle onde piane
progressive o in onde sferiche) ![]() .
.
Se prendiamo un valore
particolare della ![]() il valore di u0 resta fissato e vale
il valore di u0 resta fissato e vale ![]() .
.
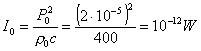
abbiamo così ottenuto il
valore di I0 precedentemente usato (che è anche uguale a W0).
![]()
In queste condizioni è
facile da verificare che ![]() .
.
Ovviamente fuori dal caso
di onda piana progressiva le relazioni vengono meno. E’ già stato verificato
che in un tubo i valori p e v
si alternano. Non è solo il caso del tubo, ma semplicemente in ogni stanza
reale, dove i valori di I, D, P, u, sono leggermente diversi in ogni punto. Una
grandezza comunque è limitata : ![]() , la prima è l’energia che si propaga (e interferisce con
l’energia riflessa), mentre la seconda è un’energia vera e propria, e dunque
somma sia dell’energia che si propaga e dell’energia riflessa.
, la prima è l’energia che si propaga (e interferisce con
l’energia riflessa), mentre la seconda è un’energia vera e propria, e dunque
somma sia dell’energia che si propaga e dell’energia riflessa.
Possiamo dunque
utilizzare questa differenza ![]() per stimare la
propagazione teorica di un suono in un ambiente.
per stimare la
propagazione teorica di un suono in un ambiente.
Ricordiamo che le
grandezze sono omogenee e solo in prima approssimazione rappresentano
l’energia. In un ambiente minimamente riflettente, ogni grandezza ha una storia
a parte.
In un tubo ad onde
stazionarie per esempio non possiamo legare mai LI per esempio a LP.
![]() varia da punto a
punto, mentre
varia da punto a
punto, mentre ![]() dipende dal termine a.
dipende dal termine a.
La norma ISO9614 è da
considerarsi in questo senso obsoleta
in quanto usa come metro di campione proprio la differenza ![]() invece che la più
corretta
invece che la più
corretta ![]() .
.
Sorgente Sonora Lineare
Consideriamo adesso il
caso di una sorgente sonora non più puntiforme, ma lineare. I fronti d’onda
adesso non sono più sferici, ma cilindrici.
Questo argomentazione
permette la trattazione di strade, ferrovie, linee di trasporto in generale,
visto che si propagano in modo lineare.
Al fine del calcolo del
livello equivalente obbliga a scomporre un singolo evento in una serie di
piccoli, ma continui eventi.
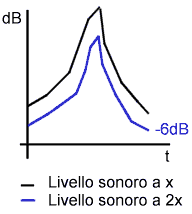
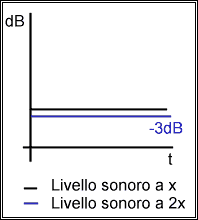
Figura 5
I due segnali sono però
profondamente differenti: se raddoppio la distanza dal primo il livello scende
di 6dB, se mi allontano dal secondo solo di 3dB:
![]() dove con s ho indicato la densità di energia (energia
prodotta da 1 m)
dove con s ho indicato la densità di energia (energia
prodotta da 1 m)

Figura 6
DL2=3dB
Se mi allontano da
un’autostrada (sorgente lineare) il livello sonoro scende di 3dB/raddoppio,
mentre se mi allontano da una fabbrica (sorgente concentrata) il livello sonoro
cala di 6dB/raddoppio della distanza. Mentre se per sorgenti puntiformi la
costante era ![]() ora per sorgenti
lineari la costante diventa
ora per sorgenti
lineari la costante diventa ![]() .
.
Esercizio 1:
Un’autostrada è percorsa
da una fila uniforme di soli autocarri (sorgente lineare). Calcolare il livello
sonoro in un ipotetico centro residenziale a 50m di distanza
dall’autostrada.
Lw (di un
autocarro) = 100 dB
Effettuando l’approssimazione
di eventi continui, utilizzando V e il numero di veicoli che passano in un’ora,
posso calcolare la distanza tra un camion e l’altro che sarà d = 80m.
![]()
![]() dB
dB
![]() su unità di
lunghezza
su unità di
lunghezza
![]() dB
dB
![]() dB
dB
ESERCIZIO
2:
Un’onda stazionaria che si propaga in un tubo chiusa ad una estremità (vedi Figura )
·
LI = 83 dB
·
LD = 88 dB
Determinare
il coefficiente d’assorbimento α e il livello di pressione massima LPmax :
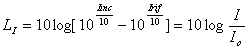
![]()
![]()
Quindi:
![]()
![]()
![]()
![]() W/m2
W/m2 ![]() W/m2
W/m2
![]()
Per
trovare il livello di pressione massima devo sommare le pressioni dell’onda
incidente e dell’onda riflessa, in pratica quando si ha un’interferenza
costruttiva.
![]() dB
dB ![]() dB
dB
![]() dB
dB
In
questo esercizio se fosse stato α=0 avremmo ottenuto LD =88 dB e Linc =85dB=Lrif ed LP =91 dB