Yuri Ferrari – matr 130964
Lezione del 29/10/2001
Ora 16,30 – 18,30
Il
condizionatore
Il condizionatore si basa
sul principio di condizionamento dell’aria; questo è l’insieme dei trattamenti
necessari per portare e mantenere l’atmosfera di un ambiente, o dell’abitacolo di
un veicolo, in condizioni caratterizzate da valori prestabiliti e fra loro
indipendenti di dati fattori, quali che siano le condizioni esterne.
Il condizionamento prevede il controllo di almeno tre dei fattori che intervengono a influenzare l’atmosfera di un ambiente e che sono: temperatura, umidità relativa e grado di ionizzazione.

Un
condizionatore (vedi figura sopra) normalmente comprende una ventola, una
serpentina di raffreddamento, una serie di alette e una sezione di post
riscaldamento. La ventola è necessaria per facilitare l’afflusso d’aria; in
figura è rappresentata da una potenza ![]() entrante.
Successivamente la serpentina di raffreddamento (per esempio il condensatore di
una macchina frigorifera) asporta un calore per unità di tempo
entrante.
Successivamente la serpentina di raffreddamento (per esempio il condensatore di
una macchina frigorifera) asporta un calore per unità di tempo ![]() all’aria, in modo da
portarla alla temperatura di rugiada. Le alette che si trovano subito dopo
hanno il compito di raccogliere la condensa formatasi a causa del
raffreddamento, formando acqua che viene incanalata in un tubicino (e poi
scaricata oppure raccolta in bottiglioni per essere usata come acqua
distillata). L’aria, dopo le alette, è satura e troppo fredda per essere
immessa in un ambiente (perché la condensazione richiede calore per avvenire,
che viene sottratto dalla corrente d’aria), quindi passa attraverso l’ultima
sezione del condizionatore, chiamata di post-riscaldamento, che fornendo il
calore per unità di tempo
all’aria, in modo da
portarla alla temperatura di rugiada. Le alette che si trovano subito dopo
hanno il compito di raccogliere la condensa formatasi a causa del
raffreddamento, formando acqua che viene incanalata in un tubicino (e poi
scaricata oppure raccolta in bottiglioni per essere usata come acqua
distillata). L’aria, dopo le alette, è satura e troppo fredda per essere
immessa in un ambiente (perché la condensazione richiede calore per avvenire,
che viene sottratto dalla corrente d’aria), quindi passa attraverso l’ultima
sezione del condizionatore, chiamata di post-riscaldamento, che fornendo il
calore per unità di tempo ![]() scalda l’aria e la
rende adatta ad essere immessa nell’ambiente.
scalda l’aria e la
rende adatta ad essere immessa nell’ambiente.
L’apparecchio
è ideato anche per poter funzionare durante la stagione invernale come pompa di
calore: in tal caso riceve dall’esterno il calore di vaporizzazione e immette
nell’interno il calore di condensazione.
Esistono
anche condizionatori (climatizzatori) per auto che sono costituiti: da un
compressore azionato dal motore; da un evaporatore posto nell’interno
dell’abitacolo attraverso il quale si fa circolare l’aria mediante un ventilatore;
da un condensatore, applicato all’esterno, a monte del radiatore principale; e
da un dispositivo termostatico di regolazione automatica.
Vediamo
ora una serie di esercizi applicativi.
Esercizio 1:
Questo
esercizio si riferisce al sistema chiuso:
![]()
rappresenta
la massa di aria umida totale. Inoltre conosciamo anche l’umidità relativa:
![]()
Vogliamo
calcolare il calore necessario sottrarre al flusso d’aria per refrigerarlo da
30 a 10 gradi centigradi, cioè da:
![]()
a:
![]()
Infine
la pressione atmosferica vale:
![]()
Vediamo
cosa succede all’aria, identificando tutte le fasi di trasformazione sul
diagramma psicrometrico.
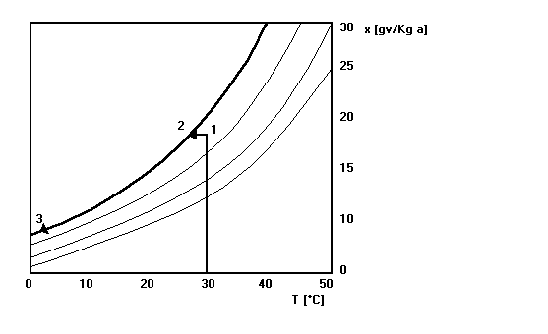
All’ingresso
del sistema l’aria è calda (temperatura T1)
e umida. All’inizio le viene tolto calore quindi la temperatura scende fino al
punto 2 (il titolo x1
rimane costante perché le masse di aria secca e vapore restano costanti),
successivamente inizia la condensazione accompagnata da un notevole
raffreddamento fino al punto 3 (temperatura T3). Inoltre anche il titolo cala (al valore x3), perché una parte del
vapore d’acqua condensa mentre la massa d’aria secca resta costante
(evidentemente quindi il rapporto MV/MA scende), mentre il grado
igrometrico rimane costantemente 1 (aria umida satura). Alla fine, come si vede
dal grafico, l’umidità sarà del 100%.
Dobbiamo
ora calcolare il calore da sottrarre all’aria e, per fare ciò, calcoliamo la
differenza delle entalpie:
in
termini specifici:
![]()
e
in termini totali:
![]()
Per
calcolare le entalpie specifiche dell’aria in 3 e in 1 dobbiamo conoscere i
titoli del punto 1 e del punto 3:
![]()
Dove
![]() è la pressione a 30°C
espressa in BAR e P è la pressione atmosferica (vedi tabella del vapore in
appendice).
è la pressione a 30°C
espressa in BAR e P è la pressione atmosferica (vedi tabella del vapore in
appendice).
Calcoliamo
ora anche il titolo nel punto 3:
![]()
A
questo punto calcoliamo le entalpie specifiche dell’aria in 1 e 3:
![]()
![]()
Ora
per calcolare il calore cercato ci manca solo conoscere la massa d’aria residua
(escluso, cioè il vapore). Possiamo, per questo, utilizzare il bilancio delle
masse, cioè: massa totale della miscela (10Kg iniziali, M) uguale alla
massa d’aria (MA) più la
massa del vapore (x1 MA),
in formula:
![]()
Per
concludere il calore necessario è:
![]()
![]()
Dove il meno sta ad indicare che il calore esce
dal sistema.
Esercizio 2:
Risolviamo
ora un esercizio sul sistema aperto.
Riprendiamo
lo stesso condizionatore dell’esercizio precedente.
![]()
rappresenta il volume complessivo dell’ambiente, che si vuole condizionare ad un volume all’ora (significa che l’intero volume d’aria deve entrare nel condizionatore esattamente una volta all’ora), quindi la portata in volume dell’aria ingresso
![]()
ed inoltre sono note le caratteristiche di questa
aria
![]()
![]()
Noto
inoltre che l’aria in uscita deve avere
![]()
![]()
e
la potenza della ventola sviluppata dalla ventola vale
![]()
determinare i calori per unità di tempo ![]() e
e ![]() scambiati nel
condizionatore.
scambiati nel
condizionatore.
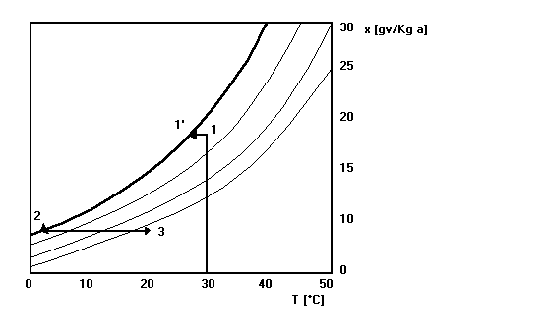
Prima
di svolgere l’esercizio guardiamo, come nell’esercizio precedente il diagramma
psicrometrico. Il ragionamento è uguale al precedente ma ora, dopo la
condensazione, l’aria molto fredda viene post-riscaldata attraverso un calore Q2. La temperatura salirà
così a T3, mentre il
nuovo valore del titolo resta costante (x2
= x3) ma cala l’umidità
relativa:
Dapprima possiamo facilmente calcolare il titolo dell’aria in ingresso (x1) come nell’esercizio precedente, quindi
![]()
e analogamente per il titolo dell’aria in uscita
![]()
D’altra parte l’aria secca è un gas perfetto, quindi
![]()
e
![]()
quindi
![]()
che rappresenta la portata
in massa di aria secca in uscita (che equivale a quella di ingresso ![]() ). Possiamo quindi facilmente trovare la portata in massa
dell’acqua condensata, come
). Possiamo quindi facilmente trovare la portata in massa
dell’acqua condensata, come
![]()
A questo punto facciamo il bilancio energetico della prima parte del condizionatore (comprendente i punti 1 e 2), ottenendo
![]()
dove hl rappresenta l’entalpia specifica dell’acqua liquida in fase di condensazione. La temperatura di quest’ultima può essere estrapolata dal diagramma psicrometrico oppure dalle tabelle dell’aria satura, ottenendo
![]()
(in realtà dalle tabelle si otterrebbe un valore del titolo, per aria satura alla temperatura di 10°C, pari a 0,00762 kgV/kgA contro i 0,0074 kgV/kgA del nostro caso, quindi con un errore ancora accettabile).
A questo punto calcoliamo le entalpie specifiche dell’aria in 1, 2 e 3, ottenendo
![]()
![]()
![]()
mentre l’entalpia specifica dell’acqua liquida condensata
![]()
di conseguenza sostituendo nell’equazione di bilancio energetico otteniamo
![]()
dove il segno meno sta ad indicare che è un calore uscente dal sistema (sottratto dall’aria) mentre il lavoro è negativo perché effettuato sul sistema.
Infine, scrivendo l’equazione di bilancio energetico per la seconda parte del condizionatore (punti 2-3) otteniamo
![]()
che rappresenta il calore che deve essere fornito alla batteria di post-riscaldamento.
Esercizio 3:
Calcolare
il calore da fornire a ![]() di aria umida a
pressione atmosferica ed umidità relativa dell’ 80% perché passi da una
temperatura di 10°C a una temperatura di 30°C. Si valutino inoltre portata
volumetrica ed umidità relativa all’uscita.
di aria umida a
pressione atmosferica ed umidità relativa dell’ 80% perché passi da una
temperatura di 10°C a una temperatura di 30°C. Si valutino inoltre portata
volumetrica ed umidità relativa all’uscita.
Si
tratta di un processo di semplice riscaldamento a pressione atmosferica
standard. Lo stato iniziale è dato da:
![]() e
e ![]()
e
quello finale da:
![]() e
e ![]()
Identificato
lo stato 1 sul diagramma psicrometrico ci si muove orizzontalmente sino ad
intersecare l’isoterma a 30°C determinando così lo stato 2. Le letture
d’interesse sono riportate in tabella:
|
Prima riga |
T [°C] |
j |
|
v |
h |
|
Stato 1 |
10 |
0,80 |
6,09 |
0,8101 |
25,38 |
|
Stato 2 |
30 |
0,231 |
6,09 |
0,8673 |
45,70 |
Dalla
relazione del calore, dato dal prodotto della portata in volume per l’incremento
di entalpia dell’aria umida, otteniamo:
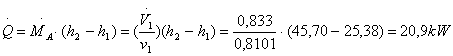
Infine ricaviamo dal bilancio delle portate in volume, la portata nel punto 2:
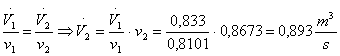
Si può notare da questo esercizio la notevole riduzione dell’umidità relativa conseguente al processo di semplice riscaldamento, e l’aumento della portata volumetrica causato da quello del volume specifico.
Esercizio 4:
In
un recipiente rigido avente un volume V di 0.08 m3 è contenuto
del vapor d’acqua in condizioni di saturazione alla pressione p1
di 1 bar. Il sistema viene raffreddato
fino a che la temperatura del vapore contenuto nella scatola raggiunge la
temperatura T2 di 72°C.
Determinare
la massa di vapore Mc che condensa durante il processo di
raffreddamento e la quantità di calore Q sottratta complessivamente al
sistema. Rappresentare la trasformazione studiata in un diagramma p-v
e in un diagramma T-s.
Essendo il vapor d’acqua inizialmente in condizioni di saturazione, conoscendo il valore della pressione nel recipiente è possibile determinare il valore assunto da tutte le proprietà termodinamiche di interesse come il volume specifico e l’entalpia.
Dalle tabelle dei vapori saturi, per p = 1 bar:
![]()
E’
dunque possibile calcolare la massa di vapore M contenuta nel
recipiente:
![]()
Il
valore di pressione nel recipiente alla fine del processo di raffreddamento è
determinabile dalle tabelle sui vapori saturi come il valore di pressione di
saturazione corrispondente alla temperatura T2.
Dalle
tabelle dei vapori saturi, per T2=72 °C:
![]()
Poiché
il raffreddamento avviene a volume costante, il valore del volume specifico non
varia durante la trasformazione (v1=v2); di
conseguenza è possibile ricavare il titolo del vapore saturo alla fine del
processo di raffreddamento come segue:
![]()
ove
si è indicato con vv e vl rispettivamente
il valore assunto dal volume specifico sulla curva limite superiore ed
inferiore alla pressione (Dalle
tabelle vv =4.655 m3/kg e vl=0.001
m3/kg).
La quantità d’acqua che
condensa nel processo di raffreddamento vale quindi:
![]()
Il valore assunto dall’entalpia specifica del vapore saturo nello stato finale è il seguente:
![]()
in cui sia il calore
latente di vaporizzazione che l’entalpia del liquido saturo alla pressione p2
sono stati calcolati da tabella (hl(p2)=301.4
kJ/kg e r(p2)=2329
kJ/kg).
Applicando il primo principio della termodinamica
per sistemi chiusi si ottiene la quantità di calore che è stata sottratta al
sistema durante la trasformazione studiata:![]()
2 1 s T 2 1 v p

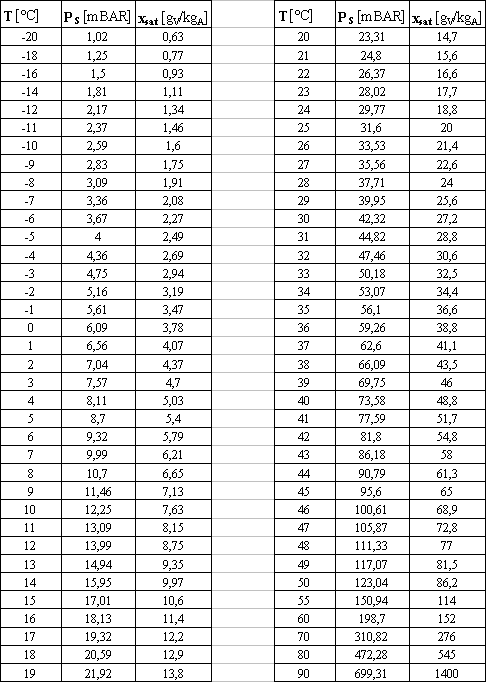
Appendice –
tabella del vapore
Viene di seguito allegata
una tabella contenente i dati fondamentali (titolo ed entalpia specifica)
dell’aria umida satura, a diverse temperature e pressione atmosferica (P = 1,013 BAR).