
INDICE
- Esercizi sui gas perfetti : - Esempio 1 pag 1
- Esempio 2 pag 4
- Calcolo delle proprietà
dei sistemi
chimicamente omogenei : - Introduzione pag 7
- Proprietà dei liquidi pag 8
- Proprietà dei vapori saturi umidi pag 12
- Esercizio di calcolo
delle proprietà dei vapori saturi umidi pag 15
ESERCIZI SUI GAS PERFETTI
ESEMPIO 1: Sollevamento di un grave
Un recipiente di superficie (A) contiene una massa (Mgas) di azoto (N2) considerato come gas perfetto. La parte superiore del recipiente, sulla quale e’ appoggiato un grave di massa (M), e’ mobile e mantiene il recipiente ad una data pressione (p1) e ad una temperatura (T1). Comunicando al gas una certa quantità di calore (Q), il gas subirà una trasformazione ISOBARA.
Supponendo di essere a livello del mare (patm = 1 BAR), si vuole:
1.calcolare il volume finale occupato dal gas;
2.calcolare il lavoro netto svolto dal sistema;
3.verificare se e’ avvenuto cambiamento di ENTROPIA nel sistema.
IMMAGINE ESPLICATIVA

DATI
|
T1 |
p1 |
M |
A |
Q |
Mgas |
|
25 °C |
3 BAR |
5 Kg |
0,5 m2 |
3,15 |
1 Kg |
SOLUZIONE
1.Utilizzando l’equazione di stato dei gas perfetti, si può scrivere:
![]() (1)
(1)
Da questa operazione si riuscirà a calcolare V2, cioè il volume occupato dal gas dopo la trasformazione. Per completare questo calcolo, però, occorre conoscere:
Mgas = 1 Kg (dato)
Rgas = 297 J/Kg K (tabella)
p2 = p1 = costante = 3 BAR (si considera una trasformazione isobara)
Proprio grazie a tale considerazione, utilizzando il primo principio in forma entalpica, si può scrivere:
![]() (2)
(2)
essendo ![]() .
.
In questo modo si calcola la temperatura T2 dopo la trasformazione:
![]() (3)
(3)
Dunque, sostituendo i valori trovati, nell’equazione di stato si avrà:
![]()
2. Per conoscere, ora, il lavoro netto svolto dal sistema, si deve considerare:
![]() (4)
(4)
da cui il grafico di figura 2:
GRAFICO

Nella relazione (4) L è il lavoro totale svolto dal sistema, sia per vincere la pressione interna, sia per cambiare temperatura:
![]() (5)
(5)
Per determinare tale valore, bisogna calcolare V1,
utilizzando l’equazione di stato per l’azoto:![]()
![]() (6)
(6)
quindi, per la (5)
![]()
L0, invece, è il lavoro svolto sul sistema dalla pressione esterna:
![]() (7)
(7)
dove:
![]()
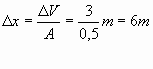
da cui per la (7)
![]()
e per la (4)
![]()
3. Poiché la pressione dello stato fisico finale coincide con quella dello stato fisico iniziale, si considera una trasformazione isobara reversibile, per cui :
![]()
e, utilizzando la definizione di entropia, si trova:
![]() =
=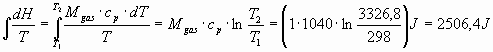 .
.
ESEMPIO 2 : Efflusso da un ugello
Una bombola di volume specifico v1 contiene un gas alla pressione p1.
Immaginando di aprire all’improvviso il rubinetto di questa bombola, si osserverà una forte fuoriuscita del gas dall’ugello.
Si vuole calcolare la velocità media w2 del gas uscente.
IMMAGINE ESPLICATIVA
w2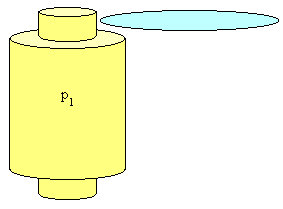
GRAFICO

fig. 4 – Rappresentazione della
trasformazione sul grafico (p,v)
DATI
|
v1 |
p1 |
|
2m3/Kg |
4,5 BAR |
SOLUZIONE
Per la risoluzione di questo problema è necessario fare delle considerazioni preliminari:
Dopo queste premesse si nota che l’energia totale è:
![]()
![]() (1)
(1)
cioè è la somma tra l’energia interna e l’energia cinetica al momento dell’apertura del foro.
Avendo considerato il processo come adiabatico reversibile si avrà, per il primo principio della termodinamica:
![]() (2)
(2)
dove l’espressione di l vale:
![]() (3)
(3)
e lo si verifica tramite considerazioni microscopiche dei fenomeni che avvengono nell’ugello.
Sostituendo il valore di l così ottenuto nella (2), risulta che:
![]() (4)
(4)
quindi
![]() (5)
(5)
e, cambiando di segno la (5), si ottiene:
![]() (6).
(6).
Ricordando che, in una trasformazione adiabatica come quella considerata, valgono:
![]() (7)
e
(7)
e 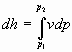 (8)
(8)
e sostituendo la (7)nella (6):
![]() (9)
(9)
quindi la (8) nella (9), si ottiene:
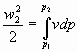 (10).
(10).
Grazie alle premesse iniziali e alle precedenti considerazioni si giunge a poter calcolare la velocità media del gas in uscita tramite l’utilizzo delle coordinate termodinamiche del gas.
Per finire, si considera l’equazione di stato del gas nel processo adiabatico:
![]() (11)
(11)
dunque
![]() (12)
(12)
dove:
![]()
![]()
Sostituendo nella (10) il valore di (v) ottenuto dalla (12), si può determinare l’integrale in dp e quindi la velocità media w2:
![]()

![]()
=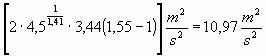
e w2 sarà:
![]()
CALCOLO DELLE PROPRIETA’ DEI SISTEMI CHIMICAMENTE OMOGENEI ( 2 )
INTRODUZIONE
Nella lezione precedente è stato introdotto l’argomento dei sistemi chimicamente omogenei, cominciando a calcolare le proprietà a partire dai gas perfetti.
In questa lezione, dopo aver provato, attraverso lo svolgimento di due esercizi, ad utilizzare le formule precedentemente descritte, si completerà la mappatura del diagramma (p,v) per le sostanze che, come l’acqua, si dilatano nel passare dallo stato liquido a quello solido ( figura 5 ). Si rivolgerà l’attenzione alle zone relative ai liquidi ed ai vapori saturi umidi e, studiandone le loro proprietà, si arriverà ad avere il quadro definitivo dei sistemi chimicamente omogenei.
GRAFICO
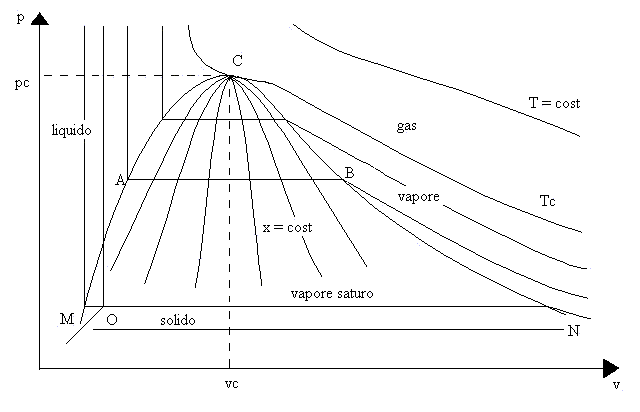
fig. 5 – Grafico (p,v) dell’acqua.
PROPRIETA’ DEI LIQUIDI
Lo stato liquido della materia si presenta come uno stato intermedio tra quello solido e quello gassoso.
Le caratteristiche di un liquido, infatti, sono molto vicine a quelle di un solido se si parla di incomprimibilità ( le densità sono inferiori solo del 10% rispetto al solido corrispondente); sono invece più vicine a quelle di un gas se si parla di libertà traslazionale e di disordine molecolare, caratteristiche, queste, evidenziate dalla tendenza dei liquidi a fluire sotto l’azione di forze applicate e dall’isotropia delle loro proprietà fisiche ( stesse proprietà fisiche in ogni punto del sistema).
Tali caratteristiche sono dovute all’impacchettamento delle molecole le quali, in forma idealizzata, possono essere viste come dei grappoli tra i cui componenti, ( gli atomi ), vi sono delle "lacune" o "buchi". Tali "lacune" non possono essere definite né in forma, né in volume, dato il continuo movimento delle molecole stesse.
Osservando il diagramma di figura 5 si nota che la fase liquida si trova nella zona compresa tra la isoterma critica "Tc" e la curva "MC" della "campana di Andrews".
In questa zona, fino a pressioni nell’ordine dei due terzi del valore che compete al punto critico, le isoterme sono ben approssimate da rette perpendicolari all’asse dei volumi specifici. Ciò vuol dire che le trasformazioni che avvengono nello stato liquido della materia ad una data temperatura, possono essere analiticamente rappresentate dalla seguente equazione di stato:
![]()
dove (v) è il volume specifico alla data temperatura.
Esistono delle tabelle che indicano i volumi specifici di alcune sostanze, corrispondenti a determinate temperature assegnate.
Nella tabella 2, ad esempio, si propone quella dell’ acqua, utilizzata per il calcolo delle proprietà del vapore saturo. Qui di seguito, invece, sempre considerando l’acqua, si propone il diagramma che ne indica i valori salienti delle densità
( ![]() )
alle varie temperature ( T ), (figura 6 ):
)
alle varie temperature ( T ), (figura 6 ):
GRAFICO
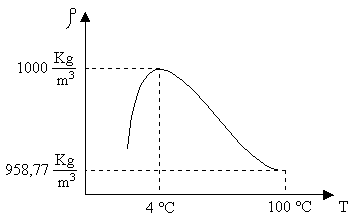
fig. 6 – Rappresentazione dei valori
assunti dall’acqua sul grafico ![]()
Si procede, ora, al calcolo delle altre proprietà.
ENERGIA INTERNA SPECIFICA
L’energia interna si esprime, ricordando il primo principio della termodinamica, attraverso la formula:
![]()
dove l’espressione del lavoro è:
![]() .
.
Dall’equazione di stato si ha, però, che:
![]() v
= cost
v
= cost ![]() dv=0
dv=0 ![]() dl=0
dl=0
quindi:
du = dq = cvdT
u = cv(T-T0).
CALORI SPECIFICI
Per i liquidi, a causa della loro incomprimibilità, non si può fare la stessa distinzione tra calore specifico a volume costante (Cv) e calore specifico a pressione costante (Cp) che è stata fatta per i gas; si avrà, perciò, un solo valore di calore specifico
Cl = Cp = Cv
La tabella 1 propone i valori di "Cl" di alcuni liquidi.
TABELLA
|
Liquido |
Cl ( J/Kg× °C) |
|
Acqua |
4180 |
|
Acqua di mare |
3925 |
|
Mercurio |
139 |
|
Glicerolo |
2390 |
|
Benzina |
2240 |
|
Petrolio |
1900 |
|
Benzolo |
1700 |
|
Cloroformio |
946 |
|
Alcool metilico |
2512 |
|
Alcool etilico |
2433 |
|
Acetone |
2211 |
|
Olio lubrificante |
1850 |
|
Olio d’oliva |
1985 |
Tab. 1- Calori specifici di alcuni
liquidi, calcolati a 20°C e
1 atm
ENTALPIA SPECIFICA
L’espressione dell’entalpia, ricavata dal primo principio della termodinamica, è:
![]()
dove:
![]()
![]()
![]()
![]()
e, integrando ambo i membri:
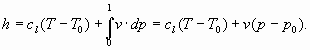
Calcolando in casi reali il valore dei due addendi che forniscono l’entalpia ci si accorge che
![]()
cioè che il calore scambiato è molto maggiore del lavoro, così che si potrebbe pensare di non considerare il valore del lavoro. Questo, però, comporterebbe un equivoco tra energia interna ed entalpia in situazioni che, nella realtà, sono molto frequenti. Un esempio è la pompa di figura 7 la quale lavora portando il liquido da una posizione di partenza, ad una posizione finale, con pressioni differenti.
IMMAGINE ESPLICATIVA

pressioni differenti
E’ dunque giusto lasciare indicata anche l’espressione del lavoro.
ENTROPIA SPECIFICA
L’espressione dell’entropia è data dal rapporto
![]()
e, in questo caso , si può giungere facilmente a calcolare la differenza di entropia (S2 –S1), tra uno stato iniziale "1" e uno stato finale"2" di un liquido, se si considera il primo principio della termodinamica in forma classica per il quale:
![]()
Si può quindi sostituire
![]() con
con
![]()
e si avrà
![]()
dove T1 e T2 sono le temperature di partenza e di arrivo dei due stati considerati nella trasformazione.
Si sono così definite tutte le formule riguardanti le proprietà dei liquidi, ma è opportuno ricordare che, per il calcolo di tali proprietà, per ogni elemento, occorre conoscere le tabelle dei valori dei volumi specifici a temperature date.
PROPRIETA’ DEI VAPORI SATURI UMIDI
Lo stato di vapore saturo umido è uno stato di transizione in cui la materia si viene a trovare ogni qualvolta passa dallo stato liquido a quello di vapore o, viceversa, dallo stato di vapore a quello liquido. Durante tale passaggio la materia è in equilibrio tra le due fasi "LIQUIDO +VAPORE SATURO SECCO" e tende ad assumere il primo stato con la diminuzione del proprio volume, o ad aumentare il proprio volume, assumendo il secondo stato.
Osservando, infatti, il diagramma (p,v) di figura 5, si nota che la fase di vapore saturo umido è tra la curva limite "MCN" della "campana di Andrews" e la linea del punto triplo "O" (punto del diagramma (p,v) in cui la materia è in equilibrio fra i tre stati solido, liquido, gassoso) ed è rappresentata da segmenti di retta paralleli all’ asse delle ascisse; ciò significa che, per determinate temperature, la pressione rimane, senza approssimazioni, costante.
Le trasformazioni isoterme che avvengono in questo stato della materia, dunque, sono anche delle trasformazioni isobare e le rette che le rappresentano degenerano una nell’altra. Pertanto, non esiste un’equazione di stato, cioè una formula chiusa che definisca analiticamente le trasformazioni in questo stato di transizione tra due fasi;
per questo motivo, al fine di facilitare i calcoli delle proprietà della materia, all’interno del campo dei vapori saturi umidi è opportuno introdurre una variabile indipendente. Questa è detta TITOLO ed è definita come la massa del vapore saturo secco, rapportata a quella del sistema:
![]()
( Sul diagramma di figura 5 sono riportate anche alcune curve caratterizzate dal valore costante del titolo e dette curve isotitolo, che si diramano tutte dal punto critico "C").
Per ogni segmento di isobara/isoterma, i titoli assumono valori
decimali che vanno da ![]() dove A è il punto in cui la materia è esclusivamente allo
dove A è il punto in cui la materia è esclusivamente allo
stato liquido ( liquido saturo )
( nel grafico (p,v), il punto si trova sul ramo inferiore della curva limite )
a ![]() dove B è il punto in cui la materia ha assunto
dove B è il punto in cui la materia ha assunto
completamente lo stato di vapore secco
( nel grafico (p,v), il punto si trova sul ramo superiore della curva limite ).
Già da questa osservazione, possiamo intuire come il titolo sia utile dal punto di vista dei calcoli: fissato un punto su un generico segmento di isobara/isoterma, infatti, il titolo sarà determinato dal rapporto tra i due segmenti contigui. In ogni caso, l’unico modo per determinare i valori delle proprietà dei vapori saturi umidi dei vari elementi, sfruttando la conoscenza dei titoli in cui calcolarle, sarà quello di disporre di alcune tabelle come, ad esempio, la tabella 2 di seguito proposta.
TABELLA
|
Tem pera tura (T) |
Pressione
(p) |
Volume Specifico del liquido (vl) |
Volume Specifico del vapore (vv) |
Entalpia Specifica del liquido (hl) |
Entalpia Specifica del vapore (hv) |
Calore di Vaporiz zazione ( r ) |
Entropia Specifica del liquido (sl) |
Entropia Specifica del vapore (sv) |
|
°C |
Atm |
m3/Kg |
m3/Kg |
Kj/Kg |
Kj/Kg |
Kj/Kg |
Kj/Kg°K |
Kj/Kg°K |
|
0 |
0,006228 |
0,0010001 |
206,3 |
0,000 |
2500,776 |
2500,776 |
0,0000 |
9,1544 |
|
10 |
0,012513 |
0,0010004 |
106,4 |
42,035 |
2519,198 |
2477,330 |
0,1511 |
8,8995 |
|
20 |
0,02383 |
0,0010018 |
57,84 |
83,903 |
2537,201 |
2453,465 |
0,2964 |
8,6663 |
|
30 |
0,04325 |
0,0010044 |
32,93 |
125,688 |
2555,623 |
2430,019 |
0,4367 |
8,4523 |
|
40 |
0,07520 |
0,0010079 |
19,55 |
167,514 |
2573,626 |
2406,154 |
0,5723 |
8,2560 |
|
50 |
0,12578 |
0,0010121 |
12,04 |
209,298 |
2591,629 |
2382,389 |
0,7038 |
8,0751 |
|
60 |
0,2031 |
0,0010171 |
7,678 |
251,124 |
2609,214 |
2358,006 |
0,8311 |
7,9084 |
|
70 |
0,3178 |
0,0010228 |
5,045 |
292,992 |
2626,380 |
2333,304 |
0,9550 |
7,7544 |
|
80 |
0,4829 |
0,0010290 |
3,408 |
334,944 |
2643,127 |
2308,183 |
1,0752 |
7,6116 |
|
90 |
0,7149 |
0,0010359 |
2,361 |
376,979 |
2659,455 |
2282,643 |
1,1924 |
7,4785 |
|
100 |
1,0332 |
0,0010435 |
1,673 |
419,099 |
2675,784 |
2256,685 |
1,3071 |
7,3545 |
|
110 |
1,4609 |
0,0010515 |
1,210 |
461,543 |
2691,275 |
2229,890 |
1,4185 |
7,2386 |
|
120 |
2,0245 |
0,0010603 |
0,8017 |
503,672 |
2706,348 |
2202,675 |
1,5278 |
7,1297 |
|
130 |
2,7544 |
0,0010697 |
0,6683 |
546,677 |
2720,583 |
2174,204 |
1,6345 |
7,0271 |
|
140 |
3,685 |
0,0010798 |
0,5087 |
589,083 |
2733,980 |
2144,898 |
1,7392 |
6,9304 |
|
150 |
4,854 |
0,0010906 |
0,3926 |
632,207 |
2746,541 |
2114,334 |
1,8418 |
6,8383 |
|
160 |
6,302 |
0,0011021 |
0,3068 |
675,331 |
2757,845 |
2082,514 |
1,9427 |
6,7508 |
|
170 |
8,076 |
0,0011144 |
0,2426 |
719,292 |
2768,731 |
2049,439 |
2,0419 |
6,6666 |
|
180 |
10,225 |
0,0011275 |
0,1939 |
763,254 |
2778,360 |
2015,107 |
2,1395 |
6,5858 |
|
190 |
12,800 |
0,0011415 |
0,1564 |
807,634 |
2786,315 |
1978,682 |
2,2358 |
6,5075 |
|
200 |
15,857 |
0,0011565 |
0,1272 |
852,432 |
2793,014 |
1940,582 |
2,3308 |
6,4818 |
|
210 |
19,456 |
0,0011726 |
0,1043 |
897,650 |
2798,038 |
1900,389 |
2,4246 |
6,3577 |
|
220 |
23,659 |
0,0011900 |
0,08606 |
943,705 |
2801,388 |
1857,683 |
2,5179 |
6,2848 |
|
230 |
28,531 |
0,0012087 |
0,07147 |
990,178 |
2803,063 |
1812,884 |
2,6101 |
6,2132 |
|
240 |
34,140 |
0,0012291 |
0,05967 |
1037,489 |
2803,063 |
1765,574 |
2,7022 |
6,1425 |
|
250 |
40,56 |
0,0012512 |
0,05006 |
1085,637 |
2800,969 |
1715,332 |
2,7934 |
6,0721 |
|
260 |
47,87 |
0,0012755 |
0,04215 |
1135,041 |
2796,364 |
1661,322 |
2,8851 |
6,0014 |
|
270 |
56,14 |
0,0013023 |
0,03560 |
1185,283 |
2789,665 |
1604,382 |
2,9764 |
5,9298 |
|
280 |
65,46 |
0,0013321 |
0,03013 |
1236,781 |
2779,617 |
1542,836 |
3,0681 |
5,8573 |
|
290 |
75,92 |
0,0013655 |
0,02554 |
1289,953 |
2766,219 |
1476,266 |
3,1610 |
5,7828 |
|
300 |
87,61 |
0,0014036 |
0,02164 |
1344,800 |
2749,053 |
1404,253 |
3,2548 |
5,7049 |
|
310 |
100,64 |
0,001447 |
0,01832 |
1402,159 |
2727,282 |
1325,122 |
3,3507 |
5,6233 |
|
320 |
115,12 |
0,001499 |
0,01545 |
1462,031 |
2700,067 |
1238,037 |
3,4495 |
5,5354 |
|
330 |
131,18 |
0,001562 |
0,01297 |
1526,089 |
2665,736 |
1139,647 |
3,5521 |
5,4412 |
|
340 |
158,96 |
0,001639 |
0,01078 |
1594,752 |
2621,774 |
1027,022 |
3,6605 |
5,3361 |
|
350 |
168,63 |
0,001741 |
0,008803 |
1671,371 |
2564,415 |
893,044 |
3,7786 |
5,2117 |
|
360 |
190,42 |
0,001894 |
0,006943 |
1761,387 |
2481,098 |
719,711 |
3,9163 |
5,0530 |
|
370 |
210,53 |
0,00222 |
0,00493 |
1893 |
2331 |
438,4 |
4,1137 |
4,7951 |
Tab.2 – Proprietà dell’ acqua e del vapore saturo.
In queste tabelle, il più delle volte, non sono riportati direttamente i valori delle proprietà dei vapori umidi, bensì i valori delle caratteristiche del liquido e del vapore secco corrispondenti nei vari titoli. Ad ogni modo, disponendo di tali dati, si giunge facilmente a determinare le proprietà dei vapori saturi umidi attraverso l’uso di alcune relazioni che sfruttano la proprietà additiva.
Bisogna, però, avere ben presente il fatto che qui non si può parlare di valori medi specifici ( e quindi di coordinate termodinamiche ), ma solo di valori medi pesati: le grandezze-funzione dello stato fisico sono, infatti, i valori corrispondenti alle condizioni limite "l" e "v" , che dipendono solo dalla pressione (o dalla temperatura) e non dipendono dalla ripartizione della massa tra le fasi. Si possono scrivere, pertanto, le seguenti formule:
volume:![]() ;
;
entalpia:![]() ;
;
entropia:![]() .
.
Dividendo e moltiplicando tali espressioni per (Ml+Mv) si ricavano, infine, le relazioni utili, con l’aiuto delle tabelle, alla determinazione delle proprietà:
VOLUME: ![]()
dove vv-vl = vd
ENERGIA INTERNA:
dalla definizione di entalpia si ha:![]()
quindi ![]()
dove ![]()
ENTALPIA: ![]()
dove ![]()
ENTROPIA: ![]()
dove ![]() .
.
A questo punto si possono definire i valori, appena introdotti, di vd, ud, hd sd:
vd rappresenta la variazione di volume conseguente alla vaporizzazione completa, a pressione costante, dell’unità di massa di liquido; tale grandezza prende correttamente il nome di volume specifico differenziale;
ud viene detto anche energia interna specifica differenziale e può essere determinato, utilizzando le grandezze sopra introdotte, attraverso la seguente relazione:
ud = r-plvd ;
hd, trattandosi di una trasformazione a pressione costante, rappresenta la quantità di calore che è necessario fornire all’unità di massa di liquido per vaporizzarla completamente; è detta anche calore latente di vaporizzazione e, nella tabella 3, è indicata con il simbolo "r";
sd viene calcolato con la seguente relazione:
![]()
in quanto, per effetto dell’equilibrio liquido vapore, si ha la corrispondenza delle trasformazioni isobare ed isoterme.
Si dispone, ora, di tutti gli elementi per provare a risolvere un semplice esercizio sul calcolo delle proprietà dei vapori saturi umidi.
ESERCIZIO
Si considera dell’acqua a pressione p e allo stato di vapore saturo umido, in un determinato titolo x.
Si vuole calcolare il valore della temperatura "T" , dell’entalpia specifica "h", dell’entropia specifica "s" e del volume specifico "v" cui si trova l’acqua sul titolo x considerato.
DATI
![]()
|
p |
x |
|
50 BAR |
0,7 |
SOLUZIONE :
T=263 °C
Si può verificare la validità di tale risultato provando a calcolare il valore di sd attraverso l’utilizzo della sua definizione:
![]()
dunque si è avvicinato il valore precedentemente calcolato (sd=3,0672 Kj/Kg)!
![]()