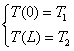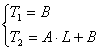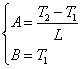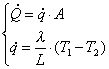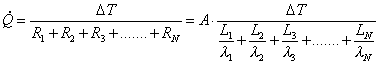TRASMISSIONE DEL CALORE

 

 

 


INDICE

 

ü      La termocinetica e gli scambi di calore                                                            1

ü      Equivalente termico della legge di Ohm                                                           3

ü      La Conduzione e la legge di Fourier                                                                5

ü      L’equazione di Fourier                                                                                   7

ü      Applicazioni                                                                                                 10

ü      Appendice                                                                                                   14

 

 

 

LA TERMOCINETICA E GLI SCAMBI DI CALORE

 

La trasmissione del calore è oggetto di studio di ben determinate branche fisiche e non solo fisiche, una di queste è la termocinetica. Questa scienza studia i fenomeni termici da un punto di vista particolare: la velocità con cui avvengono gli scambi termici. Questa caratteristica la rende sostanzialmente differente dalla termodinamica, che pure studia gli stessi fenomeni termici, ma allo stesso tempo le leggi fondamentali che regolano quest’ultima permangono rigorosamente. Infatti lo scambio di calore tra due corpi è regolato da due fondamentali leggi:

1.      il calore passa dal corpo a temperatura più alta al corpo a temperatura più fredda in accordo con il principio zero della termodinamica;

2.      il calore ceduto dal corpo più caldo è interamente assorbito dal corpo più freddo, senza dispersioni, in accordo con il primo principio della termodinamica;

queste regole, quindi, sono ancora valide in termocinetica e in questo essa è del tutto uguale alla termodinamica. In termodinamica però, non si pone attenzione al tempo impiegato per uno scambio termico, ma solo alla quantità interessata dallo scambio stesso, ecco che allora l’attenzione è incentrata sull’energia; al contrario la termocinetica pone l’attenzione sulla potenza, potenza termica in questo caso misurata in Watt (W), del processo termico, ovvero il rapporto tra l’energia scambiata e il tempo impiegato per lo scambio. A questo proposito sono stati introdotti simboli particolari che stanno ad indicare la dipendenza dell’unità di misura in questione dal tempo. Ad esempio, la potenza riferita all’unità di tempo è: . D’ora in poi si utilizzeranno di continuo questi semplici simboli per indicare il riferimento all’unità di tempo.

Lo scambio di calore tra due corpi a temperature differenti, o tra due parti di uno stesso corpo sempre a temperature differenti, può avvenire sostanzialmente in tre modi: per conduzione, per convezione e per irraggiamento.

La conduzione del calore tra due corpi, come suggerisce il nome, avviene quando gli stessi corpi entrano in contatto tra di loro; a questo punto le molecole del corpo a temperatura maggiore, dotate di energia cinetica più alta essendo essa proporzionale alla temperatura, disperdono parte della loro energia verso le molecole del corpo più freddo finché anche queste ultime non hanno raggiunto un livello di temperatura, e quindi di “agitazione termica”, di equilibrio termico. Questo fenomeno è peculiare dei materiali solidi e, in generale, di quelle strutture cristalline che imprigionano le molecole permettendo loro solo brevi spostamenti.

 

Figura 1: scambio termico per conduzione

 

 

Al contrario la convezione è un processo termico tipico dei fluidi, liquidi o gas che siano, come aria o acqua. Quando un fluido entra in contatto con un corpo a temperatura elevata (l’esempio di una pentola bollente piena di acqua è perfetto!) nei punti più vicini al corpo avviene una diminuzione della densità che, grazie alla spinta di Archimede, fa salire una parte del fluido; questo vuoto è colmato dal fluido sovrastante, più freddo e quindi più denso, che scende instaurando così un movimento convettivo. Questo movimento fa sì che il calore si sposti dal corpo caldo verso l’alto fino ad un eventuale corpo a temperatura più bassa posto sopra al fluido (come può essere l’aria che sovrasta la nostra pentola d’acqua!).

 

Figura 2: scambio termico per convezione

 

 

Un fenomeno molto particolare, è invece l’irraggiamento; esso infatti non necessita di alcun mezzo in quanto lo scambio di calore è dovuto ad onde elettromagnetiche. Infatti il corpo più caldo sprigiona, sotto forma di radiazioni, il calore che viene assorbito dal corpo più freddo. Un esempio molto importante di irraggiamento che ci riguarda da vicino è lo scambio di calore tra Sole (evidentemente il corpo caldo!) e Terra (il corpo che assorbe il calore).

 

 

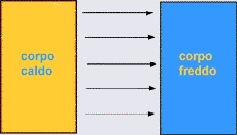
Figura 3: scambio termico per irraggiamento

 

Chiaramente, nella vita di tutti i giorni, questi tre fenomeni termici possono, e nella maggior parte dei casi lo fanno, coesistere; infatti è del tutto normale assistere a processi interagenti come ad esempio il passaggio di calore tra due corpi separati da aria posti a breve distanza tra di loro: l’irraggiamento e la convezione agiscono simultaneamente. Un altro esempio può essere rappresentato da un fluido molto trasparente nel quale si instaura, oltre alla normale convezione, un lieve fenomeno di irraggiamento. La coesistenza o meno di questi processi è dovuta principalmente alle caratteristiche fisiche e chimiche dei materiali interessati dallo scambio di calore. Questo caso è molto importante perché ci aiuta a comprendere uno dei principi più importanti legati alla termocinetica: l’equivalente termico della legge di Ohm.

 

 

 

EQUIVALENTE TERMICO DELLA LEGGE DI OHM

 

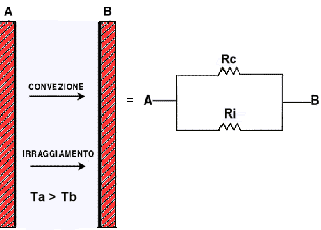
Come abbiamo detto, quasi sempre non esiste un solo modo di scambiare calore. Ad esempio: torniamo a prendere due corpi separati da uno strato di aria, come ad esempio possono essere due pareti, che si trovano a temperature differenti; come si vede dalla figura sottostante, il calore viene scambiato sia per irraggiamento che per convezione in quanto tra le due pareti non c’è il vuoto, bensì un fluido come l’aria. Questi due fenomeni, quindi, in questo caso si sommano con il risultato che il calore scambiato in totale è dato dalla semplice addizione dei due singoli apporti; questo chiaramente si ripercuote sulla potenza termica del sistema che, quindi, sarà data dalla somma delle singole potenze termiche di irraggiamento e di convezione:

 

         (1)             

 

Figura 4: effetti termici ed elettrici equivalenti (collegamento in parallelo)

 

 

Il sistema studiato può essere visto, per analogia, come un collegamento in parallelo di due resistenze (vedi figura 4) in cui alla potenza termica si sostituisce la corrente circolante nei due rami del circuito. Infatti la corrente totale è data dalla somma delle singole correnti, quella passante per RC dovuta alla convezione e quella passante per RI dovuta all’irraggiamento. Prima di generalizzare, passiamo ad un altro semplice esempio.

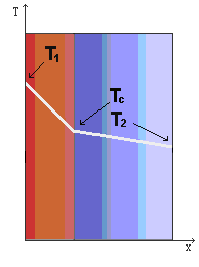
Consideriamo un tipico muro di una casa, costituito da tre strati di materiale differente, in cui le due superfici sono a temperature diverse. Il calore in questo caso è scambiato unicamente per conduzione, ma ogni materiale “reagisce” diversamente allo scambio di calore: il risultato è che si hanno tre diversi fenomeni di conduzione, ognuno indipendente, o quasi, dall’altro. A questo punto non possiamo più vedere il sistema come tre resistenze in parallelo perché i fenomeni non si sommano; questa volta il circuito analogo è dato dalle tre resistenze poste in serie (vedi figura 5) e di conseguenza la potenza termica totale non è più data dalla somma, bensì dalla seguente relazione:

 

        (2)  

 

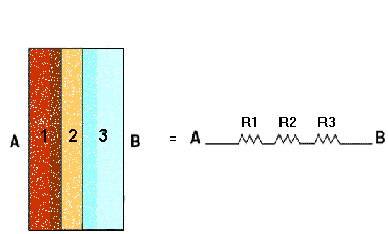
Figura 5: effetti termici ed elettrici equivalenti (collegamento in serie)

 

 

 

è allora chiaro che il calore dissipato è minore in questo caso rispetto ad un sistema simile al precedente (figura 4) e questo è appunto il principio seguito dai costruttori edili per minimizzare le perdite di calore. Giunti a questo punto, possiamo generalizzare il nostro ragionamento.

Esiste dunque una corrispondenza tra fenomeni termici e fenomeni elettrici; questa analogia è una vera e propria legge fisica e prende il nome di equivalente termico della legge di Ohm. Essa afferma che la quantità di calore scambiata nell’unità di tempo, ossia la potenza termica, è direttamente proporzionale alla differenza di temperatura che causa lo scambio di calore. Traducendo in simboli otteniamo:

 

     (3)

 

in cui per DT intendiamo la differenza di temperatura misurata in Kelvin (K). Di conseguenza, definiamo RT come resistenza termica, ovvero l’analogo della resistenza elettrica vista per i circuiti; la sua unità di misura quindi è:

 

 

diversamente dalla resistenza elettrica, quindi, la resistenza termica non ha una unità di misura propria, ma svolge lo stesso compito della resistenza elettrica nella legge di Ohm. Giunti a questo punto, però, dobbiamo fare un importante considerazione: la legge di Ohm si basa sulla proporzionalità tra caduta di potenziale e corrente, ovvero la resistenza elettrica è una costante; la stessa cosa però non si può dire della resistenza termica, in quanto essa dipende dalla temperatura, e questo comporta non pochi problemi. Per porvi rimedio ci sono due possibili strade: la prima, detta a temperature imposte, è quella di lavorare con temperature iniziali e finali costanti, in modo da poter ritenere costante la resistenza termica e non avere problemi matematici; la seconda, detta a flusso imposto, è una strada “per tentativi”: infatti il dato iniziale non sono le temperature ma la potenza termica scambiata e questo non garantisce che la resistenza termica sia costante; si deve così procedere imponendo una temperatura e, alla fine dei calcoli, controllare il risultato; se esso è accettabile il compito è svolto, se non lo è si deve ricominciare cambiando il valore imposto alla temperatura e così di seguito. Purtroppo, i problemi di questo tipo sono molto frequenti in termocinetica e questo fa capire perché questa branca della fisica sia tutt’oggi considerata una materia inesatta e approssimata!

Concludendo, abbiamo introdotto una nuova legge che regola gli scambi di calore, ma essa non ci deve sembrare strana in quanto non è altro che la trasposizione, con le dovute attenzioni e le approssimazioni che il caso impone, di una tra le più famose leggi fisiche, quella di Ohm, in ambito termocinetico. Riassumendo:

 

Fenomeni termici                                             Fenomeni elettrici

 

DT = RT ·                                          Þ        DV = R · I

 

Potenza termica ()                              Þ        Corrente (I)

 

Differenza di temperatura (DT)               Þ        Differenza di potenziale (DV)

 

Resistenza termica (RT)                          Þ        Resistenza elettrica (R)

                                                      

                                          

 

CONDUZIONE E LEGGE DI FOURIER

 

Abbiamo già parlato in precedenza della conduzione termica, ma il discorso va certamente approfondito. Innanzitutto, quando si parla di scambio di calore per conduzione bisogna distinguere questi fenomeni in due classi: se tutti i parametri in gioco (temperatura, pressione, ecc.) sono indipendenti dal tempo abbiamo a che fare con processi di tipo stazionario; al contrario, se queste grandezze, soprattutto la temperatura, dipendono dal tempo siamo di fronte a processi non stazionari, o transitori. È facile comprendere che le leggi valide per i processi stazionari non lo sono per quelli transitori che, quindi, vanno affrontati in modo differente.

La legge sicuramente più importante che regola questo tipo di fenomeni stazionari è la Legge di Fourier:

 

           (4)

 

dove per  si intende la densità di flusso termico, ovvero la potenza termica per unità di superficie (/A). Di conseguenza le sue dimensioni sono:

 

                                                                     

 

inoltre il gradiente, anche indicato con Ñ (nabla), è inteso come:

 

     (5)

 

ovvero un vettore che, avendo come componenti le derivate spaziali del campo termico scalare T(x,y,z,t), è in ogni punto del corpo diretto verso le temperature crescenti; è dunque giustificata la presenza del meno nella legge di Fourier, in quanto il vettore flusso termico specifico  deve avere una direzione concorde al verso in cui fluisce il calore, ossia verso le temperature decrescenti.

Infine, il coefficiente di proporzionalità tra gradiente delle temperatura e densità di flusso termico è espresso dal termine l chiamato conducibilità termica. Essa non è una grandezza vettoriale, ma scalare ed è propria di ciascun materiale. Le sue dimensioni sono:

 

[l]  =

 

facilmente ricavabili dalla legge di Fourier. La conducibilità termica classifica i diversi materiali in isolanti e conduttori termici a seconda del suo valore più (conduttori) o meno elevato (isolanti). In generale gli isolanti hanno una l<1. Per una maggiore precisione e informazione si consulti la tabella in appendice.

La conducibilità termica di ciascun materiale è, però, influenzata dalla stessa temperatura e ciò è dovuto alla sua dipendenza dalle caratteristiche fisiche e chimiche dei singoli elementi. Ad esempio, al crescere della temperatura, alcuni materiali isolanti aumentano la loro conducibilità, mentre certi conduttori, a causa della rottura dei legami cristallini perdono proprietà di condurre calore. Questo comporta una ulteriore difficoltà nella risoluzione del problema, ma la legge di Fourier continua ad essere valida. In questo caso si deve operare ancora “per tentativi” impostando arbitrariamente dei valori di temperatura, ricavando la conducibilità termica dalle tabelle come quella in appendice, risolvendo il problema con questi dati, ricalcolando da essi le temperature e, infine, confrontando il risultato con le condizioni iniziali poste arbitrariamente. Se il risultato è accettabile abbiamo finito, altrimenti si deve procedere iterativamente fino a quando non si ottengono risultati sufficientemente stabili.

La dipendenza di l dalla temperatura segue un andamento lineare e precisamente:

 

    (6)

 

dove l0 rappresenta la conducibilità a zero gradi e b è la variazione di l0 per ciascun grado centigrado. Generalmente la presenza di una b positiva è tipica di una sostanza gassosa, al contrario una b negativa è prerogativa di una sostanza solida, dotata quindi di reticolo cristallino. A seconda di b inoltre, la conducibilità può essere ritenuta costante o no: nella maggior parte dei casi essa è irrilevante rispetto al termine l0 rendendo esatta l’approssimazione a costante della conducibilità termica.

 

 

 

L’EQUAZIONE DI FOURIER

 

Torniamo ora alla legge di Fourier che avevamo lasciato in precedenza; questa legge, così descritta, non può essere d’aiuto in tutti i problemi di termocinetica: avevamo, infatti, sottolineato il legame di questa legge con i fenomeni stazionari, ovvero quei problemi in cui la temperatura non dipende dal tempo. Questo vincolo rappresenta il motivo per cui non possiamo utilizzare la legge di Fourier anche nei fenomeni transitori, nei quali la temperatura dipende dal tempo. Per questo tipo di problemi possiamo utilizzare però una importante equazione differenziale che prende il nome, nemmeno a farlo apposta, di equazione di Fourier. Come abbiamo detto, essa è una vera e propria equazione differenziale e, come tale, per essere risolta necessita delle condizioni iniziali, dette in altro modo condizioni al contorno; esse possono essere di due tipi:

·          condizioni di tipo T, ovvero condizioni sulle temperature; in questo caso si lavora a temperature imposte.

·          Condizioni di tipo Q, ovvero condizioni sulla quantità di calore scambiata; in questo caso si lavora a flusso imposto.

Non rimane allora che descrivere questa importante equazione. Per ottenerla, partiamo da un esempio particolare che man mano ci porterà alla formulazione dell’equazione valida in generale.

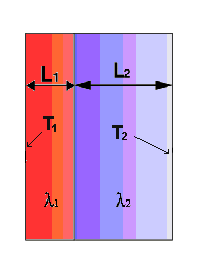
Supponiamo quindi di considerare una lamina di spessore costante L e di larghezza e lunghezza tanto grandi da essere considerate infinite; poniamo poi questa lamina in un sistema di riferimento cartesiano (come mostrato in figura 6) opportuno in modo da rendere la lastra un sistema monodimensionale nella sola variabile x. Ipotizziamo le due facce della lamina rispettivamente alle temperature T1 e T2, ad esempio con T2 < T1, e supponiamo che le pareti siano costituite da materiale con densità volumetrica r e conducibilità termica costante l. Consideriamo infine di lavorare con un elemento di lamina di area A pari ad 1 m2 e spessore dx.

 

                                              

Figura 6: lamina infinita

 

 

Il volume dell’elemento con cui lavoriamo quindi è:

 

               (7)

 

di massa pari a:

 

    (8)

 

indichiamo poi con Tx = T(x, t0) la temperatura della prima facciata al tempo iniziale t0 e con Tx+dx = T(x, t0 + dt) la temperatura della seconda parete dopo un certo lasso di tempo dt, inteso come il tempo impiegato dal calore a passare dalla prima parete alla seconda; chiaramente, dipendendo la temperatura dal tempo, avremo che:

 

  (9)

 

a questo punto, prendiamo in considerazione il bilancio energetico del fenomeno: in prima istanza possiamo notare che l’energia coinvolta nell’esempio è puramente costituita dal calore scambiato in quanto non c'è alcun lavoro svolto o subito da parte del sistema; quindi sarà:

 

= Qx – Qx+dx            (10)

 

che, espressa in funzione della densità di flusso termico, diventa:

 

              (11)

 

ora però, la quantità di calore scambiata può essere vista come il prodotto tra la differenza di temperatura dT, il calore specifico c e la massa coinvolta nello scambio dM, dunque:

 

   (12)

 

che, dalla (8) diventa:

 

      (13)

 

semplificando otteniamo:

 

      (14)

 

A questo punto, utilizziamo la legge di Fourier per semplificare le densità di flusso termico e cioè, utilizzando le seguenti formule:


 


otteniamo dalla (14):

 

      (15)

 

Che, semplificando i dx e notando che stiamo lavorando in un sistema monodimensionale e che quindi il gradiente non è altro che la derivata, diventa:

 

            (16)

 

conosciuta come equazione di Fourier.

Se poi ci spostiamo nel campo tridimensionale, le considerazioni sinora fatte, anche se molto più complesse come è facile prevedere, sono ancora valide e portano alla formulazione dell’equazione generale di Fourier:

 

      (17)

 

Questa equazione è valida in tutti i fenomeni termocinetici, non solo quelli transitori ma anche quelli stazionari; è quindi un’equazione generale valida in ogni occasione.

Ipotizziamo allora di trovarci in regime stazionario e, quindi, di avere la temperatura costante nel tempo; questo significa che la sua derivata rispetto al tempo è nulla e questo, nella formula (17), ci porta a:

 

         (18)                

 

conosciuta come equazione di Laplace. Ecco che allora abbiamo ottenuto tutte le equazioni che ci servono in qualsiasi problema di scambio di calore; da qui si ricavano tutti i casi più semplici e particolari.

Torniamo allora a ritroso fino a considerare il problema da cui eravamo partiti: la lamina indefinita. Facciamo un’ulteriore ipotesi considerando il fenomeno come stazionario; ora abbiamo tutto quello che ci serve. Infatti, dalla (18), otteniamo, nel caso monodimensionale:

 

                   (19)

 

da semplici considerazioni di analisi matematica, se la derivata seconda è nulla la derivata prima è costante e la funzione è una retta, otteniamo che:

 

           (20)

 

e grazie alle condizioni al contorno precedentemente introdotte possiamo dire:

 

                

 

e quindi ottengo la temperatura in funzione dello spostamento all’interno della lamina, questa funzione è detta profilo di temperatura:

 

            (21)  Þ                  (22)

 

possiamo infine trovare la densità di flusso termico che attraversa la lamina utilizzando la legge di Fourier:

 

                       (23)

 

 

 

APPLICAZIONI

 

 

ESERCIZIO 1

 

Calcolare la potenza termica dispersa, causata dal calore che fuoriesce dall’interno di un edificio, attraverso una parete di gesso spessa 5 cm e avente una superficie di 10 m2, sapendo che la temperatura all’interno e all’esterno valgono rispettivamente 20 °C e 0 °C.

Innanzitutto riassumiamo brevemente i dati:

 

A=10 m2

L=5 cm=0,05 m

T1=20 °C

T2=0 °C

 

 

 

Osservando la tabella in appendice ricaviamo il valore della conducibilità termica del gesso: l = 0,5 W/m K.

A questo punto possediamo tutti i dati che ci servono per ricavare la densità di flusso termico uscente dalla formula (25), ovvero: la conducibilità termica l, lo spessore della parete L e la differenza di temperatura DT (da notare che la differenza è indipendente dall’utilizzo o meno della scala Kelvin!); allora:

 

 

 

banalmente poi si ricava la potenza termica dissipata, moltiplicando la densità per la superficie A considerata:

 

 

 

 

ESERCIZIO 2

 

Affianchiamo una parete, spessa 10 cm e avente conducibilità l2 = 1,5 W/m K,  a quella di gesso dell’esercizio 1.

I dati del problema riassunti sono:

 

A=10 m2

L1=5 cm=0,05 m

L2=10 cm=0,10 m

l1=0,5 W/m K

l2=1,5 W/m K

T1=20 °C

T2=0 °C

 

 

Figura 7: equivalenza tra fenomeni termici ed elettrici nell’esercizio 2

 

 

In questo caso, lavorando con l’equazione di Fourier ci imbatteremmo in onerosi calcoli di integrazione che ruberebbero tempo prezioso; un metodo altrettanto utile, ma in questo caso molto più semplice, è rappresentato dall’utilizzo dell’equivalente termico della legge di Ohm. Riprendendo quindi il concetto di resistenza termica, possiamo vedere i due strati come due resistenze in serie, quindi, dalla (3) ricaviamo:

 

           ma sapendo che              otteniamo l’espressione che ci serve:

 

            (E.1)           

 

utilizzando quindi la (E.1), possiamo calcolare le due resistenze termiche che entrano in gioco:

 

                    

 

 

Essendo R1 e R2 in serie la resistenza equivalente è:

 

             

 

A questo punto, utilizzando la (3), calcolo la potenza termica totale scambiata dal sistema, che è data da:

 

 

Se confrontiamo questo risultato con quello dell’esercizio precedente, notiamo come il calore dissipato sia inferiore; questo ragionamento è alla base della costruzione edilizia in quanto le pareti sono costruite proprio seguendo questi criteri: più strati composti da materiali differenti aiutano ad evitare dispersioni eccessive di calore attraverso le pareti delle abitazioni. Come può essere spiegato questo fenomeno? Basta vedere che la resistenza termica aumenta, essendo la risultante di una somma, e questo comporta una minore potenza dissipata grazie alla proporzionalità inversa esistente tra le due grandezze, evidenziata nella formula (3).

Il ragionamento fatto in questo problema può essere tranquillamente generalizzato a più di due strati; in generale, dati N strati differenti valgono comunque le seguenti relazioni:

 

         (E.2)

in cui per:

·        A intendiamo la superficie della parete;

·        Li e li  intendiamo, rispettivamente, gli spessori e le conducibilità termiche dei singoli strati;

·        Ri intendiamo le resistenze termiche proprie di ciascun strato;

·        DT intendiamo la differenza di temperatura esitente tra le due facce esterne della parete.

 

 

 

ESERCIZIO 3

 

Consideriamo i dati dell’esercizio 2. Questa volta però si chiede di calcolare la temperatura, chiamata per semplicità Tc, esistente nel punto di contatto tra i due strati. 

 

Anche in questo caso esistono vari modi di procedere, ma il metodo migliore rimane l’utilizzo dell’equivalente termico della legge di Ohm. Riscriviamo innanzitutto per comodità i dati forniti dal problema:

 

A=10 m2

L1=5 cm=0,05 m

L2=10 cm=0,10 m

l1=0,5 W/m K

l2=1,5 W/m K

T1=20 °C

T2=0 °C

 

L’equivalente elettrico della differenza di temperatura, come possiamo vedere dallo specchietto a pagina 5, è la differenza di potenziale, quindi dovremo utilizzare questa analogia per i nostri scopi. Abbiamo detto che il circuito elettrico analogo allo scambio in questione è un collegamento in serie di due resistenze, allora possiamo ricavare la differenza di potenziale ai capi della prima resistenza con la formula del partitore di tensione, avremo quindi:

 

 

    (E.3)

                                                  Þ                (E.4)

   (E.4)

 

A questo punto, l’unica incognita è rappresentata dalla temperatura Tc, se la isoliamo otteniamo:

 

 

 

Proviamo ad analizzare il risultato ottenuto: la temperatura passa da 20 °C a 0 °C ma dopo un terzo del percorso è già scesa ad 8 °C; questo significa che la variazione di temperatura non segue un andamento lineare lungo tutto il percorso e questo era prevedibile, essendo i due strati differenti fisicamente. All’interno dei singoli strati, però è ragionevole pensare che l’andamento sia lineare in quanto le proprietà chimico-fisiche rimangono inalterate. Allora possiamo dire che il calo più vistoso si ha nel primo strato e questo è supportato dal fatto che la sua conducibilità termica l è minore di quella del secondo strato; in poche parole esso si comporta da isolante e, non a caso, questo fenomeno è chiamato isolamento interno. Se avessimo avuto una situazione opposta, quindi lo strato esterno che si comporta da isolante avendo una l minore, si sarebbe parlato di isolamento esterno. Per comprendere meglio questo ragionamento si veda la figura qui sotto, in cui è illustrato il fenomeno dell’isolamento interno presente nel problema appena studiato.

 

Figura 8: isolamento interno

                                                                        

APPENDICE

 

In questa appendice troviamo una tabella informativa su alcune conducibilità termiche l, calcolate a temperatura ambiente se non espressamente specificato, che si possono incontrare durante lo svolgimento di esercizi di termocinetica.

 

 

 

Materiale

l [Wm-1K-1]

Metalli e leghe

 

 

Acciaio

46 ¸50

Acciaio con 5% Ni

29

Acciaio con 30% Ni

105

Alluminio

210

Argentana (Rame, Nichel, Zinco)

27

Argento

405

Bronzo

58¸65

Ferro

67

Ferro elettrolitico

87

Ferro ed acciaio

46.5/58

Ghisa

50

Manganina

23

Nichel

58¸65

Oro

299

Ottone

110

Piombo

35

Platino

70

Rame

380

Sodio

125.60

Stagno

61

Zinco

110

 

 

 

Materiali e solidi diversi

 

 

Amianto in fogli

0.067

Asfalto

0.64

Basalto

1.27¸3.5

Calcari

0.7¸1.1

Carbone

0.14¸17

Carbone di storta

4

Carbone in polvere

0.12

Cartone

0.14¸0.23

Cartongesso in lastre

0.21

Caucciù

0.13¸0.23

Celluloide

0.35

Cellulosa compressa

0.24

Cemento

1.7

Cemento in polvere

0.07

Cenere

0.069

Creta

0.9

Diamante

»2000

Duralluminio

160

Gesso

0.4

Ghiaccio (0 oC)

2.1

Gomma

0.15

Grafite

4.9

Granito

3¸4.2

Incrostazioni di caldaia

1.16¸3.49

Intonaco di calce e gesso

0.7

Lana di vetro

0.04

Legno (media)

0.2

Lana (media)

2.1

Linoleum

2.1¸3.5

Marmo

0.18

Mica

0.39

Muratura di pietrame

1.4¸2.4

Muratura refrattaria 200o C

0.7¸0.9

Muratura refrattaria 1000° C

1.2¸1.4

Naftalina

0.37

Neve

0.06

Pietra arenaria

1.3¸1.75

Pietra calcare compatta

0.7

Pietra calcare granulosa

0.95

Polistirolo espanso

0.04

Porcellana

0.8¸1.05

Sabbia asciutta

0.35

Sabbia con 7% di umidità

1.16

Vermiculite

0.075

Vetro comune

0.95

 

 

 

Liquidi

 

 

Acqua

0.59

Acqua pesante 10¸100 oC

0.56¸0.65

Alcool

0.21

Glicerina

0.22

Olio da motori

0.12

Mercurio liquido a 0 oC

8.13

Mercurio liquido a 60 oC

9.64

Mercurio liquido a 120 oC

10.92

Mercurio liquido a 160 oC

11.6

Mercurio liquido a 222 oC

12.78

Petrolio

0.11

 

 

 

Gas (condizioni normali)

 

 

Aria

0.024

Idrogeno

0.175