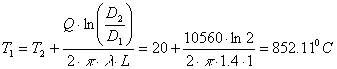ESERCIZI D’ESAME
Nota:
La personalizzazione dei dati di ingresso in funzione
del numero di matricola è fatta assegnando una opportuna variabile intera a
ciascuna cifra del numero, con nome letterale A,B,C,D,E,F.
Ad esempio, il numero di matricola 128674 dà luogo ad A=1, B=2, C=8, D=6, E=7,
F=4. I dati del problema sono assegnati in funzione di tali variabili, che
possono venire giustapposte onde ottenere numeri con
più di una cifra. Esempi:
Lunghezza
= 3 + 0.5*C (m) = 3 + 0.5 * 8 = 7 m
Massa
= 0.27+0.05 * DE (kg) = 0.27 + 0.05 * 67 = 3.62 kg
Si noti che DE
non significa D * E, quindi DE = 67, e non 6*7=42
Esame 24 del 14/09/2001
1° Esercizio –
Termodinamica (tolleranza +/- 10%)
Due correnti di aria umida confluiscono in un collettore, da cui fuoriesce una terza corrente miscelata. Non si hanno scambi termici o di lavoro con l'esterno. Note le proprietà delle due correnti in ingresso, determinare le proprietà della corrente in uscita.
Portate in massa in ingresso ![]() Ma1
= 2+0.1*F = 2.6 kg/s
Ma1
= 2+0.1*F = 2.6 kg/s
Ma2 = 1+0.2*E = 2 kg/s
Temperature in ingresso T1 = 30+D = 34 °C
T2 = 10+C =13 °C
Gradi igrometrici ![]() 1
= 0.1+0.09*C = 0.37
1
= 0.1+0.09*C = 0.37
![]() 2
= 0.2+0.02*B = 0.24
2
= 0.2+0.02*B = 0.24
Determinare:
- Grado igrometrico corrente di
uscita
____ (3 punti)
- Temperatura corrente di uscita ____ °C (3 punti)
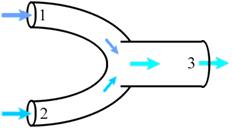
Per ipotesi non si hanno scambi termici o di lavoro con l’esterno, quindi Q=0, L=0
Ma3 = Ma1+ Ma 2 = 4.6 kg/s
I titoli delle correnti d’aria umida in ingresso sono:
![]()
![]()
![]()
![]()
![]()
dove ![]() e
e ![]() sono le
pressioni di saturazione dell’aria umida alle temperature di 34°C e 13°C rispettivamente.
sono le
pressioni di saturazione dell’aria umida alle temperature di 34°C e 13°C rispettivamente.
![]()
![]()
![]()
![]()
![]()
L’equazione di bilancio energetico mi permette di calcolare J 3 :
H3= H1 +H2 ![]() Ma3J 3 = Ma1J1+
Ma 2J2
Ma3J 3 = Ma1J1+
Ma 2J2
inoltre sono in grado di calcolare le entalpie specifiche delle 2 sezioni d’ingresso:
![]()
![]()
![]()
![]()
![]()
![]()
e poichè
![]()
risolvendo questa equazione ottengo ![]()
Ora posso facilmente ottenere
![]()
![]()
![]()
dove ho preso dalle tabelle la pressione di saturazione ![]()
2° Esercizio –
Fluidodinamica (tolleranza +/- 20%)
Trovare
lo sforzo risultante esercitato dal vento alla base dei pali di una linea
telefonica, nell’ipotesi che lo stesso soffi in
direzione ortogonale alla linea. I pali sono alti 12m e distano l’uno
dall’altro 60m, e la velocità del vento è di 10 m/s.
Diametro del cavo telefonico D1 =2+0.02*BC = 2.46 mm
Diametro del palo di sostegno D2 =50+EF = 0.106 m
Temperatura dell’aria T=010+CD/4 = 18.5 °C
Determinare:
- Forza applicata dal filo al palo _____ N (3 punti)
- Forza complessiva alla base del palo _____ N (3 punti)
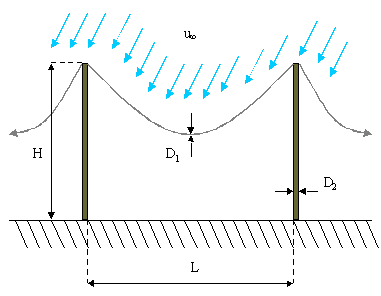
La forza applicata dal filo al palo e la forza alla base del palo (rispettivamente F1 e F2 ) sono:
![]()
![]()
dove ![]() e
e ![]() rappresentano
i coefficienti di penetrazione del filo e del palo, mentre
rappresentano
i coefficienti di penetrazione del filo e del palo, mentre ![]() e
e ![]() le loro
aree frontali e
le loro
aree frontali e ![]() la
densità dell’aria che posso calcolare:
la
densità dell’aria che posso calcolare:
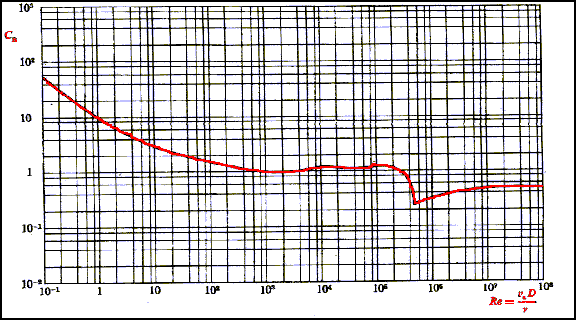
I coefficienti CR sono facilmente reperibili dal seguente diagramma che però richiede la conoscenza del numero di Reynolds :
![]()
![]()
![]() CR1 = 0.99
CR1 = 0.99
![]()
![]()
![]()
![]() CR2 =
1.2
CR2 =
1.2
Posso quindi facilmente risolvere il problema:
![]()
![]()
![]()
![]()
FTOT= F1+F2 = 96.09 N
3° Esercizio – Acustica (tolleranza +/- 0.5 dB)
Una sorgente di rumore incoerente in banda larga, puntiforme ed omnidirezionale ha livello di potenza pari a 90+C dB. Essa è situata entro un ambiente semiriverberante Sabiniano, avente un volume pari a 400+20·B m3, con superficie interna pari a 350+20·E m2, che ha coeff. di assorbimento pari a 0.2 + EF/200. Trovare il tempo di riverberazione ed il livello sonoro in un punto posto entro l’ambiente, e distante 5m dalla sorgente.
![]() dB
dB
V = 440 m3
S = 450 m2
![]()
Determinare:
- Tempo di riverberazione _____ s
- Livello complessivo lineare _____ dB
Applicando la formula di Sabin otteniamo subito:
![]()
utilizzo la legge che descrive l’andamento del livello sonoro in un campo semiriverberante:
![]()
dove il fattore di direttività è Q=1 essendo la sorgente omnidirezionale.
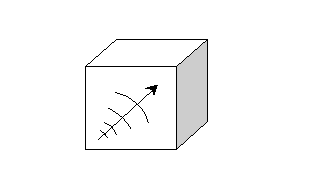
4° Esercizio – Termocinetica (tolleranza +/-
20%)
Una
sfera di acciaio, con diametro pari a 50 + CD mm, si
trova inizialmente alla temperatura di 300+EF °C. Essa viene
raffreddata mediante aria avente temperatura di 20 + B °C, e velocità di 12+C
m/s. Trovare il tempo necessario affinché la sfera di acciaio
raggiunga la temperatura superficiale di 60 °C.
Determinare:
- Coeff. di convezione ________ W/m2K
- Tempo di raffreddamento ________ s

![]()
![]()
![]()
D = 84 mm
![]()
Considero un intervallo di tempo
infinitesimo ![]() e
Studio i cambiamenti del sistema dall’istante
e
Studio i cambiamenti del sistema dall’istante
![]() all’istante
all’istante
![]() +
+
![]() :
:
All’istante ![]() il sistema aveva energia pari a
il sistema aveva energia pari a
![]() Una
parte della quale viene ceduta all’ambiente esterno tramite
scambio convettivo
Una
parte della quale viene ceduta all’ambiente esterno tramite
scambio convettivo
![]()
![]()
![]()
![]()
![]()
metto a sistema le due equazioni e risolvo l’ equazione differenziale
![]()
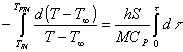
![]()
![]()
trovo il coefficiente di convezione h ricordando che siamo in regime di convezione forzata con un flusso d’aria che soffia contro una sfera
![]()
![]()
calcolo ![]() ad una temperatura media tra quella della
sfera e quella dell’aria
ad una temperatura media tra quella della
sfera e quella dell’aria ![]()
![]()
![]()
quindi l’incognita h dalla formula è :
![]()
e da qui ricavo ![]() ,
ricordando che
,
ricordando che ![]() e
il volume della sfera è
e
il volume della sfera è ![]()
![]()
![]()
Esame 22 del 12/07/2001
1° Esercizio –
Termodinamica (tolleranza +/- 10%)
In un ambiente è contenuta aria umida, alla temperatura di 20+E °C e grado igrometrico pari a 0.3+F/20. La temperatura viene ridotta, a titolo costante, sino al punto di rugiada. Determinare la quantità di calore sottratta per kg di aria secca.
- Temperatura di rugiada _______ °C (3 punti)
- Calore sottratto _______ kJ/kga (3 punti)
Calcolo il titolo:
![]()
questo
resta costante fino al punto di rugiada dove ![]()
![]()
![]()
![]()
![]()
![]()
il
valore ![]() è stato preso dalle tabelle del vapor d’acqua.
è stato preso dalle tabelle del vapor d’acqua.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2° Esercizio – Fluidodinamica (tolleranza +/- 10%)
Un serbatoio di forma cilindrica ha un diametro di 2+0.1*F m e contiene acqua mantenuta ad un livello di 4 + D m. Sul fondo di esso si trova un foro circolare a spigoli vivi (β = 1), con diametro pari ad 1/20 di quello del serbatoio, per cui l’acqua comincia ad uscire. Determinare la velocità e la portata in massa del getto di acqua che fuoriesce.
- Velocità di uscita W2 _______ m/s (3 punti)
- Portata in massa Qm _______ kg/s (3 punti)
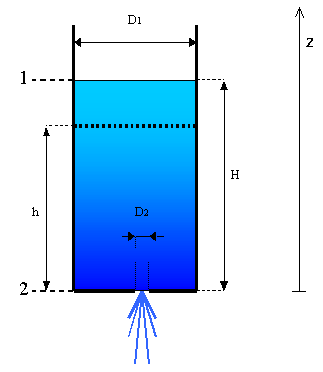
il diametro del foro è molto minore del diametro del serbatoio, quindi posso considerare l’altezza H del livello dell’acqua costante a 8m; scrivo l’equazione del bilancio energetico:
![]()
![]()
![]()
la portata
in massa ![]() dipende dal diametro del foro
dipende dal diametro del foro
![]() dove
dove![]() è la superficie del foro
è la superficie del foro
![]() :
:
![]() Kg/s
Kg/s
3° Esercizio – Acustica (tolleranza +/- 1 dB e
+/- 0.05)
Entro un tubo ad onde stazionarie (tubo di Kundt), eccitato con un tono puro a 1000 Hz, si misura un livello di intensità sonora pari a 80+C dB, ed un livello di densità dell’energia sonora pari a 85+C dB. Determinare il livello massimo di pressione ed il coeff. di assorbimento del materiale posto all’estremità del tubo.
- Livello max di pressione ______ dB (3 punti)
- Coeff. di assorbimento ______ (3 punti)
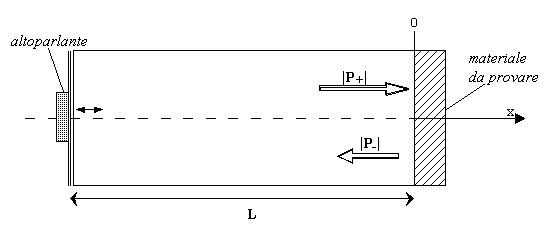
I livelli di intensità sonora e di energia sonora sono costanti in tutti i punti del tubo, ricavo allora il coefficiente d’assorbimento:
![]()
![]()
risolvo
un sistema di 2 in 2 incognite ![]() e
e ![]() :
:
![]()
![]()
![]() e
e ![]()
![]()
![]()
![]() =
0.00041524
=
0.00041524 ![]()
![]()
![]() 0.00021572
0.00021572
![]()
![]()
![]()
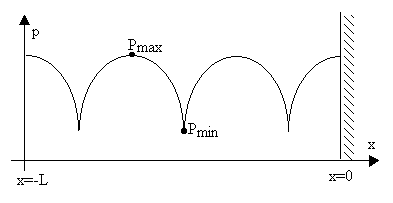
In tubo di Kundt la pressione ha un andamento oscillatorio con massimi e minimi, come in figura
![]()
![]()
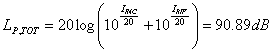
oppure possiamo anche utilizzare un altro metodo
![]()
![]()
![]()
![]()
![]()
![]()
4° Esercizio – Termocinetica (tolleranza +/-
10%)
Dentro una tubo lungo 1 m, in materiale ceramico, una resistenza elettrica genera calore per effetto Joule. La potenza generata è pari a 10000+EF*10 W. Il diametro interno del tubo è 0.02+C/100 m, quello esterno è il doppio. La conducibilità del materiale è pari a 1+0.1*D W/mK. La parete esterna è mantenuta a 20°C. Determinare la temperatura della parete interna.
- Resistenza termica del tubo ______ K/W (3 punti)
- Temperatura parete interna ______ °C (3 punti)
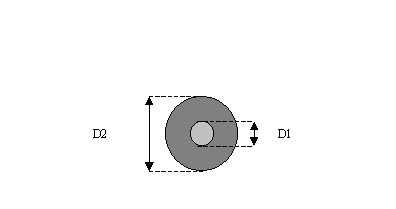
La resistenza termica del tuboè:
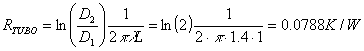
La temperatura della parete interna del tubo è:
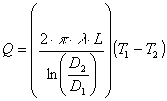
![]()